本篇文章在前面的基础上，丰富光线追踪器的各种特性。本篇内容主要包含添加纹理映射、平面光源和球形光源、三角网格模型渲染、增加天空盒背景、构建BVH树、tbb多线程渲染加速、蒙特卡罗积分方法、重要性采样，后面部分涉及的高等数学和概率论内容较多。相关的全部代码在这里。

header

  • 纹理映射
  • 三角网格模型
  • 添加光源
  • 天空盒背景
  • 构建BVH树
  • tbb多线程渲染
  • 蒙特卡罗积分
  • 重要性采样
  • MC光线追踪
  • 程序效果
  • 参考资料

一、纹理映射

  纹理映射对渲染的重要性不言而喻，为了丰富物体表面的细节，我们在这里创建一个纹理加载和采样的类。实际上，除了图片纹理，还有一些过程式产生的纹理。我们创建一个虚类$Texture$，并将$sample$类作为虚接口。然后创建子类$ImageTexture$，图片的加载我采用了stb_image库。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Texture
{
public:
    typedef std::shared_ptr<Texture> ptr;
    
    Texture() = default;
    virtual ~Texture() = default;
    virtual Vector3D sample(const float &u, const float &v, const Vector3D &p) const = 0;
};

class ImageTexture : public Texture
{
private:
    unsigned char *m_data;
    int m_width, m_height, m_channel;
    
public:
    typedef std::shared_ptr<ImageTexture> ptr;
    
    ImageTexture() = default;
    ImageTexture(const std::string &path);
    virtual ~ImageTexture();
    
    virtual Vector3D sample(const float &u, const float &v, const Vector3D &p) const;
    
};

ImageTexture::ImageTexture(const std::string &path)
{
    m_data = stbi_load(path.c_str(), &m_width, &m_height, &m_channel, 0);
    if (m_data == nullptr)
        std::cout << "Failed to load the image->" << path.c_str() << std::endl;
}

Vector3D ImageTexture::sample(const float &u, const float &v, const Vector3D &p) const
{
    int i = static_cast<int>(u * m_width);
    int j = static_cast<int>((1.0f - v)*m_height) - 0.001;
    if (i < 0) i = 0;
    if (j < 0) j = 0;
    if (i > m_width - 1) i = m_width - 1;
    if (j > m_height - 1) j = m_height - 1;
    int index = (j * m_width + i) * m_channel;
    float r = static_cast<int>(m_data[index + 0]) / 255.0f;
    float g = static_cast<int>(m_data[index + 1]) / 255.0f;
    float b = static_cast<int>(m_data[index + 2]) / 255.0f;
    return Vector3D(r, g, b);
}

  纹理坐标转换为像素数组下标要注意是否越界了，这里实现的纹理环绕方式是clamp。然后对于球体，我们要计算球体上每个点的纹理坐标，这里采用球面坐标的一个技巧。球体的上每一个点，都对应着一组唯一的方向角和天顶角$(\theta,\phi)$，我们把$(\theta,\phi)$映射到二维纹理坐标即可。映射方法如下：

  那么如何根据一个球面的点计算它的方向角和天顶角呢？从球面坐标$(\theta, \phi)$转到笛卡尔坐标$(x,y,z)$，不难理解，有如下关系：

  注意到$y/x=tan(\phi)$，所以我们可以采用下面的方式得到球面上点的天顶角和方位角：

  需要注意的是，$atan2$函数返回的角度范围是$[-\pi,+\pi]$，$asin$返回的角度范围是$[-\pi/2,\pi/2]$。

1
2
3
4
5
6
7
static void getSphereUV(const Vector3D &p, Vector2D &tex)
{
    float phi = atan2(p.z, p.x);
    float theta = asin(p.y);
    tex.x = 1 - (phi + M_PI) / (2*M_PI);
    tex.y = (theta + M_PI/2) / M_PI;
}

二、三角网格模型

  除了像球体、圆柱、圆锥等等这类有显示数学表达式的几何体，我们接触到更多的是没有表达式的网格模型。有显示的数学表达式当然好，因为我们直接直接求交点的解析解，非常准确。这里我们构建一个通用的网格模型类，它由一个个三角形构成。obj模型的导入我不再赘述，这里重点讲述了射线与三角形求交的推导过程。

  一个三角形由空间中的三个顶点$P_0$、$P_1$、$P_2$的位置表示，三角形所在平面的法向量$N$可由下式计算而得：

  平面与原点的距离$d$等于平面法向量$N$与平面中任意一点的内积的负数，这里选$P_0$，则$d$为：

  则三角形所在的平面可以用四维向量$(N, -N\cdot P_0)$表示，实际上三角形所在平面的表达式为$N\cdot(x,y,z)+d=0$，首先我们求射线与该平面的交点，然后再判断交点是否在三角形内部。将射线方程$P(t) = S+tV$带入平面的方程，则有：

  通过以上的方程我们就可以得到射线在平面$L$上的交点处的$t$值。需要注意的是，当$N\cdot V=0$时，射线与平面平行，不存在交点。然后我们把$t$值带入射线方程即可求出射线与平面的交点$P$。接下来的问题是判断点$P$是否位于三角形内部，通过计算点$P$对于三角形的三个顶点$P_0$、$P_1$、$P_2$的重心坐标可以完成该判断。重心坐标是三角形顶点加权平均值，由三个标量$\omega_0$、$\omega_1$和$\omega_2$组成，有：

  其中，$\omega_0+\omega_1+\omega_2 =1$，用$1-\omega_1-\omega_2$代替$\omega_0$，可得：

  定义以下的等式：

  将公式$(9)$带入公式$(8)$，可得：

  分别给式$(10)$两边乘$Q_1$和$Q_2$可得以下两个方程：

  写成矩阵形式如下：

  解以上关于$\omega_1$和$\omega_2$的方程，可得：

  当且仅当$\omega_0$、$\omega_1$和$\omega_2$三个权值均为非负值时，点$R$位于三角形内部，由于$\omega_0=1-\omega_1-\omega_2$，则此时应有$\omega_1+\omega_2\leq 1$且$\omega1 \geq 0\ and\ \omega_2\geq0$。若顶点$P_0$、$P_1$和$P_2$上关联有一些属性信息，如颜色、法向量或者纹理坐标，则可以利用权值$\omega_0$、$\omega_1$和$\omega_2$对这些属性信息进行插值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
bool MeshHitable::triangleHit(const Ray &ray, const float &t_min, const float &t_max,
    HitRecord &ret, const Vertex &p0, const Vertex &p1,
    const Vertex &p2, const Vector3D &normal) const
{
    float n_dot_dir = normal.dotProduct(ray.getDirection());
    // no intersection.
    if (equal(n_dot_dir, 0.0))
        return false;
    float d = -normal.dotProduct(p0.m_position);
    float t = -(normal.dotProduct(ray.getOrigin()) + d) / n_dot_dir;
    if (t < t_min || t > t_max)
        return false;
    ret.m_t = t;
    ret.m_position = ray.pointAt(t);
    ret.m_material = m_material;
    // judge inside or not.
    Vector3D r = ret.m_position - p0.m_position;
    Vector3D q1 = p1.m_position - p0.m_position;
    Vector3D q2 = p2.m_position - p0.m_position;
    float q1_squaredLen = q1.getSquaredLength();
    float q2_squaredLen = q2.getSquaredLength();
    float q1_dot_q2 = q1.dotProduct(q2);
    float r_dot_q1 = r.dotProduct(q1);
    float r_dot_q2 = r.dotProduct(q2);
    float determinant = 1.0f / (q1_squaredLen * q2_squaredLen - q1_dot_q2 * q1_dot_q2);

    float omega1 = determinant * (q2_squaredLen * r_dot_q1 - q1_dot_q2 * r_dot_q2);
    float omega2 = determinant * (-q1_dot_q2 * r_dot_q1 + q1_squaredLen * r_dot_q2);
    if (omega1 + omega2 > 1.0f || omega1 < 0.0f || omega2 < 0.0f)
        return false;
    ret.m_normal = p0.m_normal * (1.0f - omega1 - omega2) + p1.m_normal * omega1 + p2.m_normal * omega2;
    ret.m_texcoord = p0.m_texcoord * (1.0f - omega1 - omega2) + p1.m_texcoord * omega1 + p2.m_texcoord * omega2;
    if (ret.m_normal.dotProduct(ray.getDirection()) > 0.0f)
        ret.m_normal = -ret.m_normal;
    return true;
}

  既然模型是由一个个三角形组成，那么在判断射线与当前的模型是否存在交点时，我们就遍历所有的三角形，一个一个三角形与射线做相交判断：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
bool MeshHitable::hit(const Ray &ray, const float &t_min, const float &t_max, HitRecord &ret) const
{
    HitRecord tmpRec;
    bool hitAny = false;
    float closestSoFar = t_max;
    for (int x = 0; x < m_indices.size(); x += 3)
    {
        int index1 = m_indices[x + 0];
        int index2 = m_indices[x + 1];
        int index3 = m_indices[x + 2];
        if (triangleHit(ray, t_min, closestSoFar, tmpRec,
            m_vertices[index1],
            m_vertices[index2],
            m_vertices[index3],
            m_faceNormal[x / 3]))
        {
            hitAny = true;
            closestSoFar = tmpRec.m_t;
            ret = tmpRec;
        }
    }
    return hitAny;
}

三、添加光源

  光源是一种特殊的物体，一般情况下它不反射、折射光线，而是自身发射光线。因此，为了实现一个光源，当我们的射线碰撞到光源表面时，我们直接返回光源的碰撞点的颜色，不再做折射和反射。我们将发光的逻辑放到材质中，并将发光这一行为抽象为$emitted$函数。对于非光源物体，我们可以看成发出的光rgb均为0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Material
{
public:
    typedef std::shared_ptr<Material> ptr;
    
    Material() = default;
    virtual ~Material() = default;
    
    virtual bool scatter(const Ray &in, const HitRecord &rec, ScatterRecord &srec) const
    { return false; }
    
    virtual float scattering_pdf(const Ray &in, const HitRecord &rec,
                                 const Ray &scattered) const
    { return 1.0f; }
    
    virtual Vector3D emitted(const Ray &in, const HitRecord &rec, const float &u,
                             const float &v, const Vector3D &p) const
    { return Vector3D(0.0f, 0.0f, 0.0f); }
};

class DiffuseLight : public Material
{
private:
    unsigned int m_emitTex;
    
public:
    typedef std::shared_ptr<DiffuseLight> ptr;
    
    DiffuseLight(unsigned int a) : m_emitTex(a) { }
    
    virtual bool scatter(const Ray &in, const HitRecord &rec, ScatterRecord &srec) const
    { return false; }
    
    virtual Vector3D emitted(const Ray &in, const HitRecord &rec, const float &u,
                             const float &v, const Vector3D &p) const;
};

Vector3D DiffuseLight::emitted(const Ray &in, const HitRecord &rec, const float & u,
                               const float & v, const Vector3D & p) const
{
    return TextureMgr::getSingleton()->getTexture(m_emitTex)->sample(u, v, p);
}

  这样，对于任意的物体，我们都可以把它当作一个光源，只要给这个物体赋予的材质为$DiffuseLight$即可，同时要注意给发光材质设置一个纹理。

四、天空盒背景

  之前在光线投射到背景中时，我们是直接返回设定的背景颜色（或通过插值、或直接指定背景）。同样，我们可以通过天空盒来丰富我们的场景细节。天空盒的相关原理比较简单，不再赘述。一个天空盒用边长为1的立方体表示，一个立方体我采用多个三角形构成立方体网格。这里有个问题，就是如何实现天空盒永远无法靠近的效果。在实时渲染时我们直接移除视图矩阵的位移，在光追这里我们直接将光源的出发点设为原点，方向保持不变，这样的一条射线再与天空盒立方体做求交并采样纹理即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Vector3D Skybox::sampleBackground(const Ray &ray)
{
    HitRecord rec;
    Ray r(Vector3D(0,0,0), ray.getDirection());
    TextureMgr::ptr texMgr = TextureMgr::getSingleton();
    int index = -1;
    for (int x = 0; x < m_indices.size(); x += 3)
    {
        int index1 = m_indices[x + 0];
        int index2 = m_indices[x + 1];
        int index3 = m_indices[x + 2];
        if (triangleHit(r, 0.001f, FLT_MAX, rec,
            m_vertices[index1], m_vertices[index2], m_vertices[index3],
            m_vertices[index1].m_normal))
        {
            index = x;
            break;
        }
    }

    if(index != -1)
    {
        int map = index / 6;
        return texMgr->getTexture(m_cubemap[map])
                ->sample(rec.m_texcoord.x, rec.m_texcoord.y, rec.m_position);
    }
    else
        return Vector3D(0.0,0.0,0.0);
}

五、构建BVH树

  在整个光线追踪算法的渲染过程中，计算量最大的就是光线与场景图元的求交过程。如果不采用一些特殊的数据结构而只是用线性表存储场景物体的话，那么每一条射线都需要对这个存储场景物体的线性表遍历一次，这个射线碰撞检测的算法时间复杂度是$O(n)$的，当$n$比较大时，那么射线碰撞检测需要耗费绝大部分的光线追踪算法时间。射线相交检测的时间是目前光线追踪算法从理论到大规模实际应用过渡的主要瓶颈。为此，我们需要一些特殊的场景管理数据结构来加速这个过程，BVH树（全称为bounding volume hierachy，即层次包围体）是光线追踪领域常用的一种3D场景管理数据结构。它的启发思路就是通过一个简单的包围盒把物体包围起来，射线和场景中的物体求交之前，会先和这个包围盒进行求交，如果该射线没有碰到该包围盒，表明该直线一定不会和包围盒里的物体相交；如果该射线碰到该包围盒，那么再来计算射线是否和包围盒中的物体相交。我们采用包围体是AABB包围盒（即axis-aligned minimum bounding box，轴对齐的最小包围盒，简称轴向包围盒）。

  BVH树本质上是对空间做分割，然后采用二分搜索快速判断射线会与哪些包围盒发生碰撞，从而使得算法的时间复杂度从$O(n)$降到了$O(log(n))$，这是一个非常明显的算法效率的提升，特别是当$n$数量逐渐增大的时候。每一次的判断过程如下列伪代码所示。如果射线与父节点的包围盒有交点，则进一步判断子节点与射线的相交情况，否则直接退出。

1
2
3
4
if (ray hits bounding object)
    return whether ray hits bounded objects
else
    return false

  BVH树全称是层次包围盒，故名思意，它是一个树形的层次结构，父节点的包围盒包围全部子节点所在的空间，正如下图11所示。蓝色和红色的包围盒被包含在紫色的大包围盒中，它们可能重叠，并且它们不是有序的，它们只是单纯地被包含在内部。

图1 层次包围盒

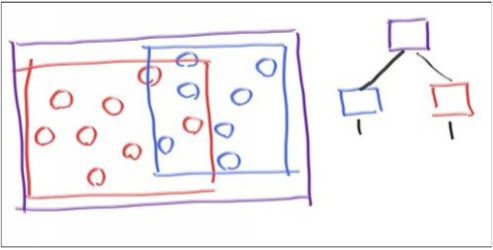
  对于图1，检测的伪代码如下：

1
2
3
4
5
6
if (hits purple)
    hit0 = hits blue enclosed objects
    hit1 = hits red enclosed objects
if (hit0 or hit1)
  return true and info of closer hit
return false

1、射线与包围盒相交判断

  我们采用的紧凑的包围盒是AABB包围盒，计算出了包围盒之后，我们还需要一个判断射线是否与包围盒相交的办法，不需要求出射线与包围盒的交点，只需判断是否存在交点即可！我们采用一种常见的”slab“方法，它是基于AABB包围盒的。三维的AABB包围盒由三个轴的区间表示，假设分别为$[x_0,x_1]$、$[y_0,y_1]$、$[z_0,z_1]$。

  对于每一个区间，我们首先判断射线在边界的投影交点情况。三维空间中，$x=x_0$和$x=x_1$是一个平面，射线在这两个平面上的交点的$x$值可以通过将$x=x_0$和$x=x_1$带入射线的方程$P(t)=S+tV$的$x$分量得到：

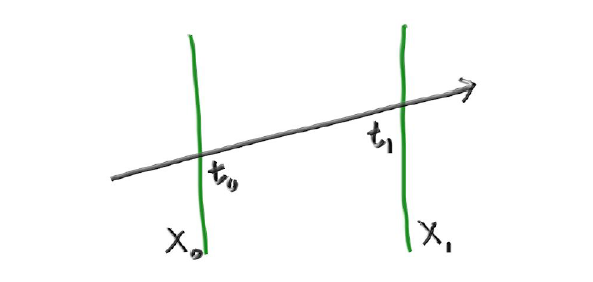
1558612929075

图2 射线与边界的交点

  从而可以求出$t_0$和$t_1$如下所示：

  关于$y$轴和$z$轴同理，我们求出了每条轴的交点分量，那么如何快速判断射线与包围盒区域是否存在相交的情况呢？为了便于理解，我们以二维的情况为例，则射线与二维的包围区域相交由如下三种情况：

图3 射线与边界相交的三种情况

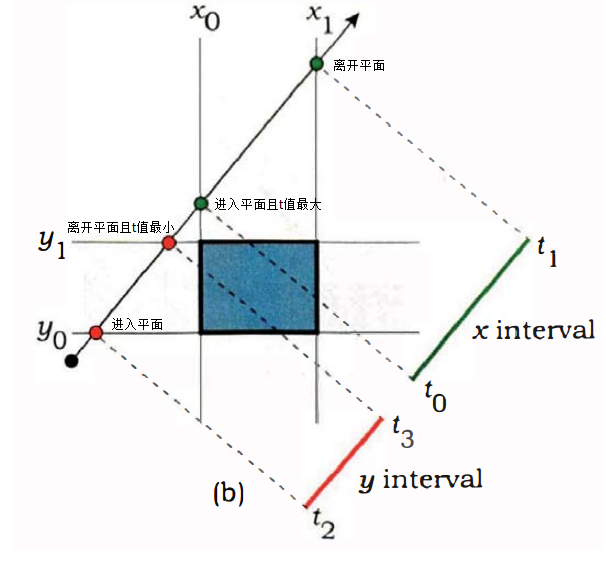
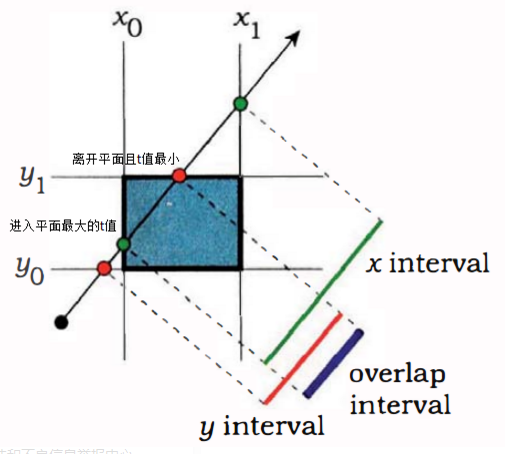
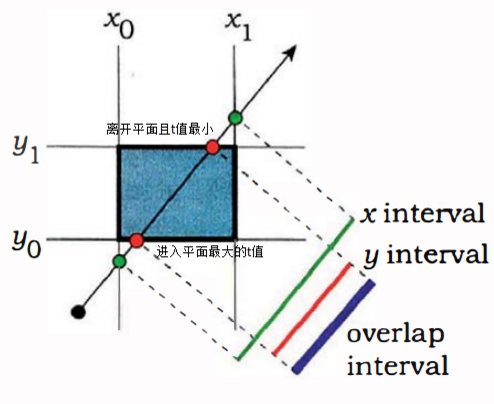
  我们求得$t$值是关于射线上的电到射线原点的距离，通过仔细观察上面的三张图片，我们可以发现在二维的情况下，当$max(t_0,t_2)>min(t_1,t_3)$时，射线一定和区域存在交点，即射线与每个轴区间的左端点中的最大$t$值大于射线与每个轴区域间的右端点中的最小$t$值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
bool hit(const Ray &ray, float tmin, float tmax) const
{
    float t0, t1, invD;
    
    // x
    invD = 1.0f / ray.getDirection().x;
    t0 = (m_min.x - ray.getOrigin().x) * invD;
    t1 = (m_max.x - ray.getOrigin().x) * invD;
    if (invD < 0.0f)
        std::swap(t0, t1);
    tmin = t0 > tmin ? t0 : tmin;
    tmax = t1 < tmax ? t1 : tmax;
    if (tmax <= tmin) return false;
    
    // y
    invD = 1.0f / ray.getDirection().y;
    t0 = (m_min.y - ray.getOrigin().y) * invD;
    t1 = (m_max.y - ray.getOrigin().y) * invD;
    if (invD < 0.0f)
        std::swap(t0, t1);
    tmin = t0 > tmin ? t0 : tmin;
    tmax = t1 < tmax ? t1 : tmax;
    if (tmax <= tmin) return false;
    
    // z
    invD = 1.0f / ray.getDirection().z;
    t0 = (m_min.z - ray.getOrigin().z) * invD;
    t1 = (m_max.z - ray.getOrigin().z) * invD;
    if (invD < 0.0f)
        std::swap(t0, t1);
    tmin = t0 > tmin ? t0 : tmin;
    tmax = t1 < tmax ? t1 : tmax;
    if (tmax <= tmin) return false;
    
    return true;
}

2、BVH树的构建

  首先我们要考虑如何构建一颗BVH树，BVH数据结构本质就是一颗二叉树。每个树节点右两个子节点，当然子节点之间不存在空间上的顺序关系。树的内部节点都不存储实际的场景物体，仅存储一个包围盒，叶子节点才存储真正的场景物体。构建BVH树的工作考虑的是如何构造一棵可以有效描述当前场景信息的二叉树。这当中的关键是如何对毫无规律地散落在场景中的众物体进行划分，即决定哪些物体该划分到左子树上，哪些物体该划分到右子树上。我们可以把这个问题抽象成一个”划分策略“——我们总会按照某种”策略“划分场景的，待会再考虑具体有哪些策略。另外，由于我们是在3D空间中工作，为了将问题简化，用分而治之的角度看，我们可以首先建立一个”原则“：即决定在哪根轴（x,y,z）上进行划分。”原则“与”策略“的不同之处在于，不管用何种”策略“，总是遵守同一种”原则“。

  决定在哪根轴（x,y,z）上进行划分，取决于场景中的物体在各个轴上分布的“散度”。如果这些物体沿着某根轴分布得最为“松散”（即落在该轴上靠一侧最近的物体与另一侧最近的物体，二者距离为最大），那么就沿该轴进行划分。还有一种方式，即采用随机的方式选取划分的轴，这样当场景物体分散的很随机时，实现的效果还不错。这里我采用随机选取一个轴的方法进行划分。

  确定了以哪根轴进行划分，接下来就要考虑“怎么划分”。我们目前暂时实现按终点划分的策略，顾名思义，取中点划分的意思就是在先前选取的轴上取其中点作为划分点，中点以左划分到左子树，中点以右划分到右子树。这种划分的实现方式最为简单，但往往效果不是太好：因为物体的分布往往不是均匀的。其中一种糟糕的情况（a）是，某侧子树上可能会拥挤过多的物体，而另一侧子树上却太少，这对查找效率影响很大。另外还有一种糟糕的情况（b），就是包围盒之间互相“重叠”（overlapped）的情况。如果两棵子树对应的包围盒“重叠”的越多，那么一条射线穿过该区域时同时击中两子树的概率也就越大，这就意味着两棵子树都得进行相交测试。当然我们目前实现的BVH树没有考虑那么多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
BVHNode::BVHNode(std::vector<Hitable *> &list, int start, int end)
{
    // sort it randomly depend on
    int axis = static_cast<int>(3 * drand48());
    if (axis == 0)
        sort(&list[start], &list[end], boxCompareX);
    else if (axis == 1)
        sort(&list[start], &list[end], boxCompareY);
    else if (axis == 2)
        sort(&list[start], &list[end], boxCompareZ);
    int length = end - start;
    if (length == 1)
        m_left = m_right = list[start];
    else if (length == 2)
    {
        m_left = list[start];
        m_right = list[start + 1];
    }
    else
    {
        m_left = new BVHNode(list, start, start + length / 2);
        m_right = new BVHNode(list, start + length / 2, end);
    }
    // bounding box.
    AABB boxLeft, boxRight;
    if (!m_left->boundingBox(0, 0, boxLeft) || !m_right->boundingBox(0, 0, boxRight))
        std::cerr << "no bounding box in BVHNode constructor\n";
    m_box = AABB::surroundingBox(boxLeft, boxRight);
}

3、BVH树的遍历

  遍历BVH差不多是件直截了当的事情。在遍历的过程中，当发现射线与某个子节点相交的话，那么有无必要再检测下与另一子节点是否相交？答案是要的。因为两个节点无法保证完全“不重叠”，如下图所示，很有可能在检测另一子节点时发现了更近的交点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
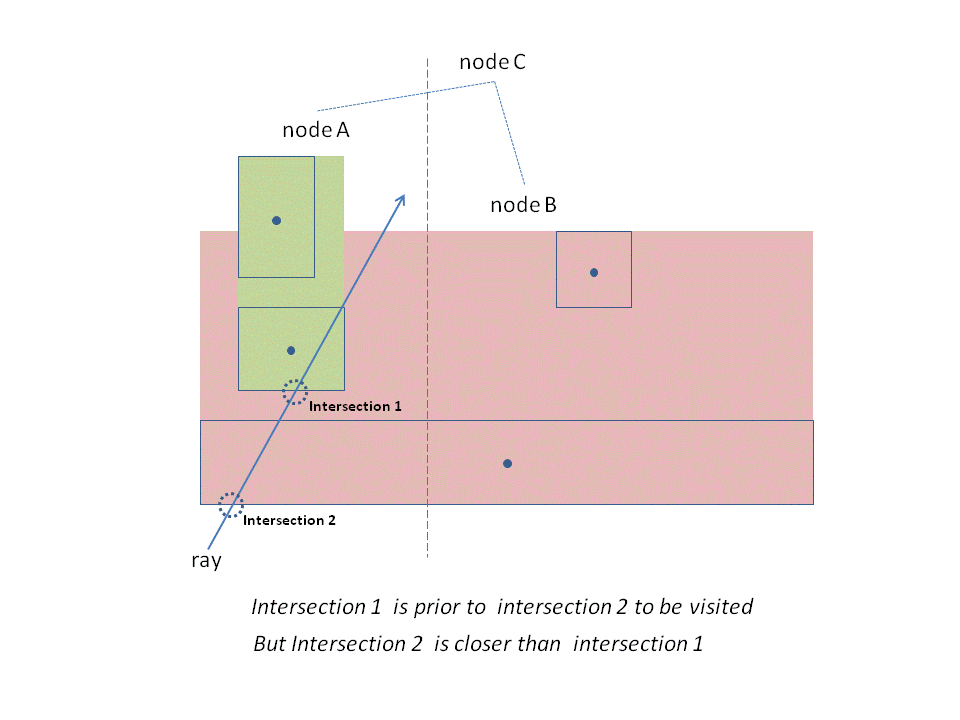
33
bool BVHNode::hit(const Ray &ray, const float &t_min, const float &t_max, HitRecord &ret) const
{
    if (m_box.hit(ray, t_min, t_max))
    {
        HitRecord leftRec, rightRec;
        bool hitLeft = m_left->hit(ray, t_min, t_max, leftRec);
        bool hitRight = m_right->hit(ray, t_min, t_max, rightRec);
        // both hit.
        if (hitLeft && hitRight)
        {
            if (leftRec.m_t < rightRec.m_t)
                ret = leftRec;
            else
                ret = rightRec;
            return true;
        }
        // only left child.
        else if (hitLeft)
        {
            ret = leftRec;
            return true;
        }
        else if (hitRight)
        {
            ret = rightRec;
            return true;
        }
        else
            return false;
    }
    else
        return false;
}

六、tbb多线程渲染

  到目前为止我们实现的光追渲染逻辑都是串行的，只能利用单核cpu运行我们的渲染程序。对于简单的场景来说，渲染的速度还是挺快的。但是当我们渲染复杂的模型时，单核光追的渲染速度慢到爆炸，渲染时间随着模型的面片数迅速增长，渲染时间动不动就数十小时！为此，我们迫切需要加速渲染程序。我们可以看到，每个像素着色之间是没有联系的，一个像素的着色值与其周围的像素计算无关，所以像素的着色计算是可以并行计算的。我们首先实现在cpu上利用多核加速我们的渲染程序。直接操纵原生的线程API不是非常好，因为这样的话我们必须知道当前电脑的核心数，并据此将循环做一个分割，以便充分利用每个cpu核心。Intel开发的TBB是非常有用的线程库，它屏蔽了底层的线程细节，自动根据我们给定的工作量做线程分割，充分利用电脑的全部cpu资源，而且使用起来也非常简单。这里利用多核线程的渲染速度加速比大致是当前电脑的核心数，也就是说，电脑的cpu核心越多，渲染速度越快。tbb的官方网站请看这里。

  tbb的全称是Thread Building Blocks，这里我们只用了tbb的parallel_for接口，它对一个给定的for循环做划分，然后每个划分并行计算。我采用的parallel_for接口函数如下所示：

1
2
template<typename Range, typename Body>
void parallel_for( const Range& range, const Body& body, const auto_partitioner& partitioner )

  可以看到出现了三个参数：range、body和partitioner。range就是我们要做并行的for循环下标范围，通常采用一维的迭代器blocked_range指定。这里我把二重循环展开成一重循环。然后body就是函数执行体，这里我通过c++11的lambda表达式指定。最后的partitioner是线程的划分方法，通常直接采用auto_partitioner。并行版的光追渲染如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void Tracer::parallelThreadRender(Hitable *scene)
{
    parallel_for(blocked_range<size_t>(0, m_config.m_height * m_config.m_width, 10000),
        [&](blocked_range<size_t>& r)
    {
        for (size_t i = r.begin(); i != r.end(); ++i)
        {
            Vector4D color;
            size_t col = i % m_config.m_width;
            size_t row = i / m_config.m_width;
            for (int x = 0; x < m_config.m_samplings; ++x)
            {
                float u = static_cast<float>(col + drand48()) / static_cast<float>(m_config.m_width);
                float v = static_cast<float>(row + drand48()) / static_cast<float>(m_config.m_height);
                Ray ray = m_config.m_camera->getRay(u, v);
                color += deNan(tracing(ray, scene, &m_samplingList,0));
            }
            color /= static_cast<float>(m_config.m_samplings);
            color.w = 1.0f;
            // gamma correction.
            color = Vector4D(sqrt(color.x), sqrt(color.y), sqrt(color.z), color.w);
            if(color.x > 1.0f) color.x = 1.0f;
            if(color.y > 1.0f) color.y = 1.0f;
            if(color.z > 1.0f) color.z = 1.0f;
            drawPixel(col, row, color);
        }
    }, auto_partitioner());
}

七、蒙特卡罗积分

  蒙特卡罗积分方法（Monte Carlo method）是数值分析中的一个重要分支，它的核心概念是使用随机性来解决确定性的问题。大数定律告诉我们，对于满足某个概率分布的随机变量，其数学期望所描述的积分可以使用这个随机变量随机抽样的样本均值来近似，因此在一定的误差范围内，我们能够使用大量的随机数来近似积分运算的结果。在计算机图形学中， 蒙特卡罗方法主要被应用于物理模拟以及光照传输中的积分运算，在离线渲染领域， 渲染方程几乎只能使用蒙特卡洛方法来进行计算。为了深入理解蒙特卡罗方法，我们首先要复习概率论相关的一些基础内容。以下的内容主要参考秦春林的那本书《全局光照技术：从离线到实时渲染》。

1、概率密度函数、概率分布函数

  概率密度函数（probability density function, 简称PDF）用于描述连续型随机变量所服从的概率分布，对于连续随机变量$X$，其概率密度函数$p(x)$是通过落于$x$附近的区间$[x,x+dx]$内的随机数的概率$p(x)dx$来定义的，然而这种定义方式并不直观，所以连续随机变量的概率分布一般通过更直观的称为概率分布函数或者累积分布函数（cumulative distribution function, 简称CDF）来定义，连续随机变量$X$的累积分布函数用大写字母$P$表示，其定义如下：

  可以看到，概率分布函数$P(y)$定义的是所有随机数的值中小于或等于$y$的随机变量的概率的积分，即理解成对于一个随机数$x$，其小于等于$y$的概率。因此，概率分布函数是一个递增函数。连续随机变量的概率密度函数$p(x)$具有以下的属性：

  其中，式$(8)$说明了$p(x)$和$P(x)$的关系，前者是后者的导数。那么给定一个随机变量的区间范围$[a,b]$，随机变量的值$x$落在这个区间的概率计算如下：

  注意，这里的$Pr$函数是概率函数，而不是概率分布函数。直观来讲，概率密度函数$p(x)$给定的并不是随机变量取值$x$的概率，概率密度函数与轴围成的面积才是给定的概率。如下所示，图(a)是概率分布函数，而图$(b)$则是概率密度函数，给定区间的$[a,b]$的概率就是下图(b)中的面积，这也对应了公式$(19)$中的积分形式（积分的几何意义就是面积）。

6

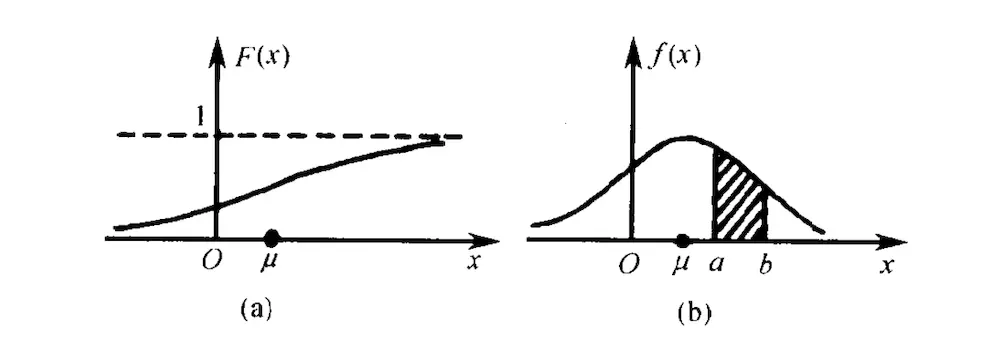
  在这里，我们要特别关注的一个分布，那就是均匀分布！对于$[a,b]$区间上的均匀分，其概率密度函数为常数$\frac{1}{b-a}$，它表示随机抽样结果落于区间$[x,x+dx]$的概率在每个$x$处都相同。均匀分布的随机变量是整个蒙特卡罗方法的基础，在计算机模拟中，通过都是由系统提供的random()函数生成某个区间内的均匀分布，然后通过一些方法将均匀分布的随机变量转换为具有任意概率密度分布的随机变量。

2、数学期望

  对于离散随机变量$X$，假设其值$x_i$对应的抽样概率为$p_i$，则该随机变量$X$的数学期望，或称为均值，为：

  数学期望代表的是对一个随机变量$X$进行抽样的平均结果。例如，对于骰子的例子，它的数学期望为：

  相应地，对于连续随机变量$X$，其期望值为随机变量值$x$与其概率密度函数$p(x)$的乘积在全定义域上的积分：

  连续随机变量$X$的数学期望为什么上面的公式$(22)$形式呢？这其实可以通过离散划分连续随便变量的定义域，然后按照离散数学期望得到一个近似的公式，当划分数趋向于无穷大且划分区间趋向于无穷小时，就是公式$(22)$的积分定义。如下所示：

  通常我们对随机变量的函数更感兴趣。考虑以随机变量$X$为自变量的函数$Y=g(X)$，我们只知道随机变量$X$的概率分布，怎样求出随机变量$Y$的数学期望值呢？我们可以通过无意识的统计规律（law of the unconsicious statistician）来求随机变量函数的数学期望：设$Y$是随机变量$X$的函数$Y=g(X)$，且函数$g$是连续函数。若$X$是离散型随机变量，它的概率函数为$P\{X=x_i\}=p_i,i=1,2,…$，则有：

  若$X$是连续型随机变量，它的概率密度函数为$p(x)$，则有：

  该方法的重要意义在于：当求$E[Y]$时，我们不必求出$Y$的分布律或概率密度函数，只需利用$X$的分布律或概率密度即可。

3、大数定律

  在统计学中，很多问题涉及对大量独立的随机变量抽样$x_i$的和进行处理，这些随机变量拥有相同的概率密度函数$p(x)$，这样的随机变量称为独立同分布的随机变量。当这些随机变量抽样的和被除以这些随机变量抽样的数量$N$时，我们就得到该随机变量的期望值的一个估计：

  随着抽象数量$N$的增大，该估计的方差逐渐减小。当$N$的值足够大时，该估计的值就能够充分接近实际数学期望的值，这样我们就能够将统计方法用于解决确定性问题。大数定律（law of large numbers）告诉我们，当$N\to\infty$时，我们可以确定随机变量的统计平均值趋近于数学期望的值，即：

  因此，随机变量的数学期望可以通过对随机变量执行大量的重复抽样来近似计算得到。

4、蒙特卡罗积分

  假设我们要计算一个一维函数的积分，如$\int_a^bf(x)dx$，数值分析方法通常采用一些近似方法来计算积分。一种最简单的求积分的方法就是采用梯形法，它通过将被积函数沿作用域上划分成多个区域，然后计算这些区域面积的和。这种方法不适用于多维积分的计算，计算机图形学领域用的最多的还是蒙特卡罗方法。大数定律用于对数学期望的积分公式进行估计，即对积分$\int_{-\infty}^{+\infty}xf(x)dx$进行估计。但是通常情况下我们要求的积分公式是对任意的一个函数积分，假设函数$g(x)$的定义域为$x\in S$（可以是一个多维空间），我们希望计算如下的积分：

  现在先不管公式$(27)$。由前面我们知道，给定任意一个关于随机变量的实数函数$f$以及服从$p(x)$概率密度函数的随机变量$x$，我们可以采用如下的公式来近似计算随机变量函数$f(x)$的数学期望：

  现在我们令公式$(27)$的被积函数$g(x)=f(x)p(x)$，则$f(x)=\frac{g(x)}{p(x)}$，那么公式$(28)$即可转变对公式$(27)$的形式，如下所示：

  可以看到通过这个变换，我们巧妙地转换成我们要求的积分公式，这就是蒙特卡洛方法求积分的核心思想。公式$(29)$的期望值为：

  而公式$(29)$的估计方差为：

  可以看到，随着$N$的增大，公式$(31)$的方差随之降低（成反比），这就是一般蒙特卡罗方法的特点。实际上蒙特卡罗方法最大的问题就是估计逼近正确结果的速度非常慢。理论上，公式$(29)$的$p(x)$函数的选择可以是任意的，这也是蒙特卡罗方法的优点，因为通常很难生成与被积函数具有一致分布的随机数。从公式$(31)$也可以看出，通过使$g(x_i)$和$p(x_i)$的比值尽可能地小也可以减少估计误差，在实践上通常我们尽可能地使$p(x)$的分布接近于$g(x)$。综上，蒙特卡洛积分方法计算任意函数的积分步骤如下：

  • 首先对一个满足某种概率分布的随机数进行抽样；
  • 使用该抽样值计算$\frac{g(x_i)}{p(x_i)}$的值，这称为该样本的贡献值；
  • 最后对所有抽样点计算的结果求平均值。

  上面的步骤中，最困难的就是怎么样对一个具有任意分布函数的随机变量进行抽样。

5、随机抽样

  首先定义什么是抽样。给定一个定于域空间$\Omega_0$及其概率密度函数$p(x)$，其中$x\in \Omega_0$，则应有：

  抽样是这样的一个算法，它能够从$p(x)$对应的随机变量$X$中产生一系列随机数$X1,X2,…$，使得对任意的$\Omega \in \Omega_0$满足如下：

  在实现中我们并不能直接从$p(x)$产生随机数，在计算机程序中这个过程必须要求首先具有某些基础随机数的一个序列。我们通常采用均匀随机数random来产生一个均匀分布的随机数，然后用来作为抽象所需的基础随机数。目前抽象方法根据不同情况有不同的方法，这里目前只介绍逆变换算法。

  逆变换算法的定义为：设$X$是连续随机变量，其概率分布函数为$P_X$，若随机变量$Y$是一个$[0,1]$上的均匀分布，则随机变量$P_X^{-1}(Y)$具有和$X$一样的概率分布。即我们通过概率分布函数的反函数来获取服从$p(x)$概率密度函数的随机变量，注意是概率分布函数$P(x)$的反函数，而不是概率密度函数$p(x)$的反函数。有时我们不知道概率分布函数，这时我们可以通过概率密度函数来求它的概率分布函数。

  逆变换算法从一个概率密度函数$p(x)$产生随机数$X_i$的步骤如下：

  • 首先计算$p(x)$的概率分布函数：$P(x)=\int_0^xp(t)dt$；
  • 其次计算累计分布函数的反函数：$P^{-1}(x)$；
  • 然后从一个$[0,1]$上的均匀分布产生一个随机数$\phi$；
  • 最后将随机数$\phi$代入$P^{-1}(x)$求出服从$p(x)$分布的随机数：$X_i=P^{-1}(\phi)$。

八、重要性采样

  重要性采样（importance sampling）是蒙特卡罗方法中最重要的方差缩减方法，它通过选择对一个与目标概率分布具有相似形状的分布函数进行抽样来减少方差。重要性采样试图在被积函数中贡献较多的区域放置更多的采样点，以体现这部分区域的重要性。给定一个概率密度函数$p(x)$以及根据该概率密度函数抽样得到的$N$个随机数$x_i$，根据蒙特卡洛方法，被积函数$f(x)$的积分$I$（即前面的公式（27），被积函数换成$f(x)$）可以通过以下公式来近似估计：

  一个理想的估计的方差应该为$0$，即：

  注意到公式$(35)$中，被积函数部分的$p(x)>0$，故应有$(\frac{f(x)}{p(x)}-I)^2=0$，从而有如下的推导：

  若我们采用公式$(36)$得到的概率密度函数进行采样，那么方差就会被完全消除。但是公式$(36)$要求我们首先计算$I$的值，而这正是我们尝试去求解的，因而行不通。但是我们可以通过选取与被积函数$f(x)$具有相似形状的概率密度函数来减少方差。选择用于抽样的概率密度函数非常重要，尽管蒙特卡罗方法本身没有限制对概率密度函数的选择，但是选择不好的概率密度函数会大大增加蒙特卡罗估计的方差。

  直观来讲，重要性采样就是根据被积函数$f(x)$的值来调整$p(x)$的概率分布。$f(x)$值大的地方，就多采样几个点；$f(x)$值小的地方，就少采样一些点。$p(x)$概率密度函数越是接近$f(x)$，蒙特卡罗方法估算的结果就越精确。

1、复合重要性采样

  在实际的情景中，计算机图形学中的被积函数通常非常复杂，它们可能是不连续的，通常在少数区间拥有奇点或者一些较大的值，所以很难找到一个简单的与被积函数相似的分布来做重要性采样。例如，我们考虑渲染中最普通的直接光源的计算公式，如下所示：

  我们可以选取$L_i$或者$f_r$来做重要性采样，但是这种方式表现效果并不佳。考虑一个接近镜面的BRDF表面被一个球形面积光照亮的例子。如下所示：

7

  若将面积光源的分布$L_i$作为重要性采样概率密度函数，因为物体表面几乎是镜面的，所以除了沿镜面反射光方向$\omega_i$，大部分光源上的采样对在最终的光照贡献都为0，因此估计的方差会非常大；而若采用BRDF分布作为重要性采样分布，那么对于小面积光源，依然会导致很大的方差。

  因此，我们通常使用更复杂的采样方式，从而降低估算的方差。通常是根据被积函数的分布特征对其进行区域划分，然后在不同特征的区域上使用不同的分布函数进行采样，最后将这些结果以某种方式进行混合。复合重要性采样就是这一类的采样方法，它提供了一个策略使得可以从多个不同的分布中采样，然后对这些不同的采样结果进行加权组合。复合重要性采样可以简单地分成以下几步：

  • 首先，选取一系列的重要性分布$p1,…,p_n$，使得对于被积函数$f$的每一个函数值比较大的区域$\Omega_i$，在这个区域$\Omega_i$，分布函数$p_i$近似为被积函数$f$。通常一个复杂的被积函数是多个不相关的简单分布的乘积形式，所以这些重要性分布来源于这些简单分布。
  • 然后，从每个分布$p_i$产生$n_i$个随机数$X_{i,1},…,X_{i,n_i}$；
  • 最后，将所有的分布估算结果通过加权组合起来。

  复合重要性采样加权组合公式如下所示：

  公式$(38)$中的$\Sigma_{i=1}^n$表明结果是由$n$个采样技术的叠加，$\frac1n_i\Sigma_{j=1}^{n_i}\omega_i(X_{i,j})\frac{f(X_{i,j})}{p_i(X_{i,j})}$即表示一种特定的采样分布$p_i$的蒙特卡罗估算结果。可以看到，这里还乘上了一个权重系数$\omega_i(X_{i,j})$，$w_i(x)$可以在每个$x$处的值不一样，只要保证对于给定的$x$值，满足$\Sigma_{i=1}^n\omega_i(x)=1$即可。

2、平衡启发式

  现在我们需要确定公式$(38)$中的权重系数计算方法。假设我们采用两个采样分布$p_1(x)$和$p_2(x)$，两个采样分布单独的采样估算结果分别为$\frac1{n_1}\Sigma\frac{f(x)}{p_1(x)}$和$\frac{1}{n_2}\Sigma\frac{f(x)}{p_2(x)}$，它们各自的方差都很大，所以我们给它们各自乘上一个系数进行加权组合。为了尽可能地发挥每个采样分布的优势，我们往往尽可能地保证在每个区域贡献较大的采样分布拥有更大的权值系数。考虑如下的权重系数函数：

  其中$c_i$是每个采样分布$p_i$对应的采样数量占比，即$c_i=\frac{n_i}{N}$，故$\Sigma_ic_i=1$，$c_i$在采样之前我们就可以确定得到。公式$(39)$被称为平衡启发式，将$c_i=\frac{n_i}{N}$和公式$(39)$代入到公式$(38)$，可以推导出如下的标准的蒙特卡洛估算方法（做一些消去）：

  其中，$\overline p(x)$又被称为联合抽样分布，其数学公式如下所示。总的采样数$N$，每个分布$p_i$采集$n_i$个随机数$X_{i,j}$。以上就是平衡启发式的核心思想，一种很自然地组合多种采样分布的方式。我们采用一个单一的与$i$无关的分布$\overline p(x)$来表述这种组合方式。

九、MC光线追踪

  了解了相关的原理，接下来我们就实现一个MC（Monte Carlo，蒙特卡罗）光线追踪，主要的参考资料是Peter Shirley的《Ray Tracing_ the Rest of Your Life.pdf》。采样方法是复合重要性采样，复合的采样分布为Lambertian材质BRDF采样分布加上光源采样分布。

1、立体角

  在球面坐标中，一个方向向量我们通常采用$(\theta, \phi)$来唯一地表示，分别是天顶角和方位角。在衡量发光强度和辐射辐射度量学中，立体角有着广泛的应用。立体角描述了站在某一点的观察者观测到的物体大小的尺度，它被定义为球表面截取的面积微分与球半径平方之比，单位为球面度，写作$sr$。显然，立体角是二维圆心角的三维扩展：

  更一般的情况，立体角通常转换为$(\theta, \phi)$来表示，在单位球体上，$d\omega=dA$，我们转换成用$(\theta,\phi)$求微分面积$dA$。我们知道二维的弧长公式为：圆心角弧度数*半径（注意圆心角要换成弧度制）。如下所示，$\theta$和$\phi$对应的弧长为：

8

图4 求弧长

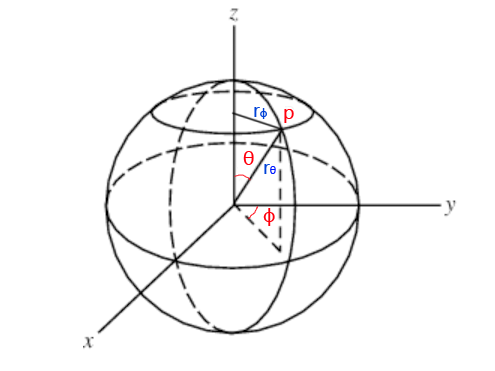
  公式$(43)$中的$r_\theta$其实就是球体半径，$r_\phi$与$r_\theta$的关系为：$r_\phi=r_\theta * sin\theta$。微分面积$dA$可以看成是一个矩形，宽和高分别为对应的弧长$d_{r_\phi}$和$d_{r_\theta}$，根据公式$(43)$我们可知$d_{r_\phi}$、$d_{r_\theta}$计算方法如下：

  对于单位球体，$r_\theta=r=1,r_\phi=r_\theta*sin\theta=sin\theta$，从而立体角微分可转换成如下表示：

2、Lambertian材质BRDF采样

  对于Lambertian材质我们假定其光线的散射分布与$cos\theta$成正比，这里的$\theta$是光线与表面法向量的夹角，也就是说在靠近法线的方向光线散射得比较多。当光线与表面法线夹角大于90度时，不发生光线散射。我们记得光线得散射概率密度函数pdf为$C*cos\theta$，其中$C$为某个常数。对于概率密度函数，我们必须保证其在全定义域上的（这里就是整个半球方向）积分为1，即有（涉及到了立体角转球面坐标表示形式和求定积分）：

  从而，Lambertian材质的光线散射概率密度函数PDF，记为$pS(direction)$，如下所示：

  现在我们要根据这个概率密度函数生成服从该分布的随机半球向量，根据前面随机抽样部分，我们首先要求出它的概率分布函数。根据定义，概率分布函数就是对概率密度函数积分：

  根据逆变换算法，我们要取概率分布函数的反函数。这里有个小技巧，我们不需要调用反三角函数得到反函数，我们只需得到$cos\theta$即可。因为即便调用反三角函数得到$\theta$，后面我们将$(\theta,\phi)$转换成笛卡尔坐标向量的时候还是要调用三角函数$cos$，我们直接避免这个比较费时的过程。所以，任取一个$[0,1]$上均匀随机数$r_2$：

  公式$(49)$只得到随机方向向量的$\theta$，我们还需要$\phi$。对于Lamberatian材质，光线在方向角上是均匀分布的，故其概率密度函数为$\frac{1}{2\pi}$，概率分布函数为$\frac{\phi}{2\pi}$。故对$\phi$的随机采样如下，任取一个$[0,1]$上的均匀随机数$r_1$：

  采样得方向向量的$(\theta,\phi)$，我们还要将其转换到笛卡尔坐标系的形式，这个过程不难理解，仔细观察图4，不再赘述。从而，服从公式$(47)$采样方向向量的代码如下所示：

1
2
3
4
5
6
7
8
9
10
 static Vector3D randomCosineDir()
{
    float r1 = drand48();
    float r2 = drand48();
    float z = sqrt(1-r2);
    float phi = 2 * M_PI * r1;
    float x = cos(phi) * 2 * sqrt(r2);
    float y = sin(phi) * 2 * sqrt(r2);
    return Vector3D(x,y,z);
}

  值得注意的是，我们的采样是以物体表面的切线和法线构成的坐标轴为参考系的，其中z轴方向是表面的法线向量。因此，通过上面的代码采样的得到方向向量还要转到该局部坐标系下。这个过程可以构建矩阵，也可以直接将方向向量三个分量与轴向量相乘，最后相加得到。我们采用了后者，首先构建一个局部坐标的正交基（Ortho-normal Bases）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class ONB
{
private:
    Vector3D m_axis[3];

public:
    ONB() = default;
    Vector3D u() const { return m_axis[0]; }
    Vector3D v() const { return m_axis[1]; }
    Vector3D w() const { return m_axis[2]; }

    Vector3D operator[](int i) const { return m_axis[i]; }

    Vector3D local(float a, float b, float c) const
    { return u() * a + v() * b + w() * c; }

    Vector3D local(const Vector3D &a) const
    { return u() * a.x + v() * a.y + w() * a.z; }

    void buildFromW(const Vector3D &n);

};

void ONB::buildFromW(const Vector3D &n)
{
    m_axis[2] = n;
    m_axis[2].normalize();

    Vector3D a;
    if(fabs(w().x) > 0.9f)
        a = Vector3D(0,1,0);
    else
        a = Vector3D(1,0,0);
    m_axis[1] = w().crossProduct(a);
    m_axis[1].normalize();

    m_axis[0] = w().crossProduct(v());
    m_axis[0].normalize();
}

  再构建一个PDF虚类，将PDF函数的函数值和采样抽线为$value$接口和$generate$接口。并继承它创建CosinePDF类，可以看到CosinePDF的$value$是按照公式$(47)$计算的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class PDF
{
public:
    virtual float value(const Vector3D &driection) const = 0;
    virtual Vector3D generate() const = 0;
};

class CosinePDF : public PDF
{
private:
    ONB uvw;

public:
    CosinePDF(const Vector3D &w) { uvw.buildFromW(w); }

    virtual float value(const Vector3D &driection) const;

    virtual Vector3D generate() const;

};

float CosinePDF::value(const Vector3D &direction) const
{
    Vector3D dir = direction;
    dir.normalize();
    float cosine = dir.dotProduct(uvw.w());
    if(cosine > 0.0f)
        return cosine / M_PI;
    else
        return 0.0f;
}

Vector3D CosinePDF::generate() const
{
    return uvw.local(Vector3D::randomCosineDir());
}

3、直接光源采样

  显然在靠近光源的方向上，光照值对物体表面的颜色贡献更大，因此直接对光源采样对减少蒙特卡洛积分的方差有非常重要的作用。直接光源采样需要我们首先求采样分布的概率密度函数，目前我们先讨论一个最简单的光源例子，即矩形光源。假设矩形光源的面积为A，那么这个矩形光源的直接均匀采样的概率密度函数PDF为$\frac1A$，但是通常我们采样的单位是立体角微分，如下所示，

9

图5 直接光源采样

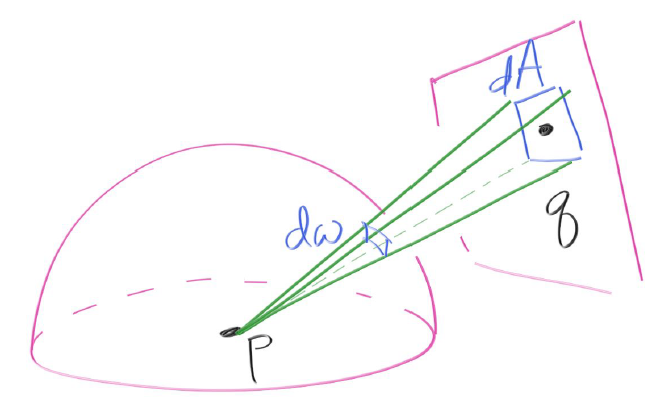
  $d\omega$与$dA$存在着一个对应关系，实际上我们可以通过前面提到的立体角定义（即公式$(42)$）得到$d\omega$与$dA$的关系如下所示，这个公式不难理解。其中$\alpha$夹角是采样方向向量与矩形表面的法线向量的夹角，$dAcos\alpha$实际上是将矩形的微分面积$dA$投影到采样方向$pq$上，这是因为从$pq$方向看去只能看到$dAcos\alpha$这个大小的面积，然后再比上半径长度的平方$||pq||^2$，这是立体角的定义。

  现在对$dA$的采样概率为$\frac{dA}{A}$，在球体方向上对立体角$d\omega$采样的概率为$p(direction)d\omega$，其中$p(direction)$是我们假定的对光源直接采样的概率密度函数。理论上来说，$\frac{dA}{A}$应该等于$p(direction)d\omega$，即有：

  公式$(52)$推导出了我们要找的直接光源采样的概率密度函数。根据逆变换算法，我们还要求它的概率分布函数从而生成服从公式$(52)$概率密度函数的随机采样方向，但是这里其实没有必要。我们直接在矩形光源上随机采样一个点，然后将这个采样点与物体表面上的点连接起来就是我们的直接光源采样方向，通过这个方法省去了比较复杂的高数推导过程。

  有了以上的理论基础，我们接下来就实现矩形的直接光源采样。我这里的定义的一个矩形平面是由两个三角形组成，默认是在xz平面上的边长为2的正方形。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Vector3D Plane::random(const Vector3D &o) const
{
    Vector3D center = m_transformation.translation();
    Vector3D leftCorner;
    float width = m_transformation.scale().x * 2.0f;
    float height = m_transformation.scale().z * 2.0f;
    leftCorner.x = center.x - m_transformation.scale().x;
    leftCorner.z = center.z - m_transformation.scale().z;
    leftCorner.y = center.y;
    Vector3D random_point(leftCorner.x + drand48() * width, leftCorner.y,
                          leftCorner.z + drand48() * height);
    return random_point - o;
}

float Plane::pdfValue(const Vector3D &o, const Vector3D &v) const
{
    
    HitRecord rec;
    if(this->hit(Ray(o,v), 0.001f, FLT_MAX, rec))
    {
        float area = m_transformation.scale().x * 2.0f * m_transformation.scale().z * 2.0f;
        float distance_squared = v.getSquaredLength();
        float cosine = fabs(v.dotProduct(rec.m_normal) / v.getLength());
        float ret = distance_squared / (cosine * area);
        return ret;
    }
    else
        return 0.0f;
}

  除了矩形区域光源，我们接下来还添加一个对球形区域光源的重要性采样。我们采取的坐标系依然是球形光源的局部坐标，而且依然是对光源区域做均匀采样。设想我们从物体表面上的一点望向一个球形区域光源，我们能够看到的区域就是我们要做均匀采样的区域，采样方法依然是围绕$(\theta,\phi)$展开，其中$\theta$是采样方向向量与物体表面的点与球心构成的方向向量的夹角。

  显然方位角$\phi$依然是$[0,2\pi]$的范围，不然我们不可能看到一个圆形。而$\theta$则需要做一些限制，它现在有个上界，如下图6所示，P是物体表面上的一点，C为球形光源的球心，R是球形光源的半径。

10

图6 球形区域光源采样

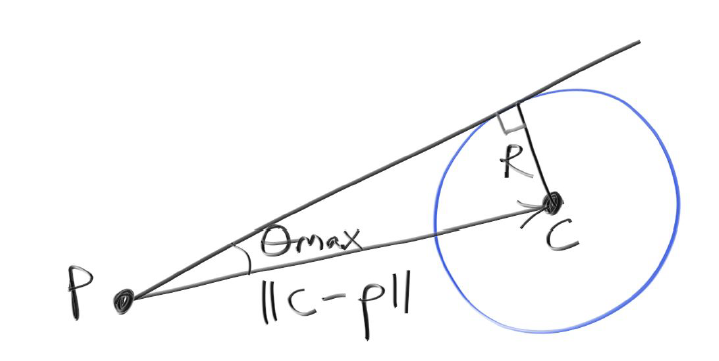
  由图6可知，$sin(\theta_{max})=\frac{R}{||C-P||}$，相应的$\theta_{max}$的余弦值如下所示：

  然后我们是对$\theta$和$\phi$做均匀采样，$\phi$的采样与前面Lambertian采样一样，这里不再赘述。对于$\theta$，因为是均匀采样，那么它的概率密度函数必然也是一个常数，我们设为$C$，那么其概率分布函数计算如下：

  根据逆变换算法，取$[0,1]$上的均匀随机数$r_2$，并结合公式$(54)$的反函数，可得采样的$cos\theta$如下：

  现在有个问题就是$C$这个具体是多少？我们已经知道$\theta$的上界$\theta_{max}$，当$\theta=\theta_{max}$时，应该取概率分布函数值$P(\theta_{max})$为1，也就是$r_2=1$。故将其代入公式$(55)$我们可以得到$C$的具体表达式：

  然后再将公式$(56)$和公式$(53)$代入公式$(55)$，可得：

  公式$(56)$j就是我们所需的概率密度函数，可以看起来不是很直观，这里我稍微解释一下。公式$(56)$其实就是我们从物体表面上的一点观测到的球形光源所占的立体角的倒数（注意，这里的立体角是以物体表面上的一点为球心而不是球形光源的球面上的立体角）！立体角的几何意义是就是单位球体上的面积，然后做一个倒数是因为我们是做均匀随机采样。立体角的求法如下所示：

  可以看到公式$(58)$求得的结果就是公式$(56)$中的分母。取球形光源上的随机一点采样算法如下，就是公式$(57)$的实现。

1
2
3
4
5
6
7
8
9
10
static Vector3D randomToSphere(float radius, float distance_squared)
{
    float r1 = drand48();
    float r2 = drand48();
    float z = 1 + r2 * (sqrt(1 - radius * radius/distance_squared) - 1);
    float phi = 2 * M_PI * r1;
    float x = cos(phi) * sqrt(1 - z * z);
    float y = sin(phi) * sqrt(1 - z * z);
    return Vector3D(x, y, z);
}

  对球形光源的随机采样以及求取概率密度函数的值如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
float Sphere::pdfValue(const Vector3D &o, const Vector3D &v) const
{
    HitRecord rec;
    if(this->hit(Ray(o,v), 0.001f, FLT_MAX, rec))
    {
        float cos_theta_max = sqrt(1- m_radius * m_radius/(m_center - o).getSquaredLength());
        float solid_angle = 2 * M_PI * (1 - cos_theta_max);
        return 1.0f / solid_angle;
    }
    else
        return 0.0f;
}

Vector3D Sphere::random(const Vector3D &o) const
{
    Vector3D dir = m_center - o;
    float distance_squared = dir.getSquaredLength();
    ONB uvw;
    uvw.buildFromW(dir);
    return uvw.local(Vector3D::randomToSphere(m_radius, distance_squared));
}

2、复合重要性采样

  上面我们分别讨论了Lambertian采样和直接光源采样，然后我们要把它复合到一起。场景中通常有多个光源，所以直接光源采样应该对多个光源进行采样，我们采取均匀随机的策略，对于一束光线，它采样哪个光源由均匀的随机数决定，这样就能雨露均沾。复合的权重套用前面提到的平衡启发式，Lambertian采样和直接光源采样的权值各0.5，也就是各占一半。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class MixturePDF : public PDF
{
private:
    PDF* m_pdf[2];

public:
    MixturePDF(PDF *p0, PDF *p1) { m_pdf[0] = p0;m_pdf[1] = p1; }

    virtual float value(const Vector3D &direction) const
    {
        return 0.5f * m_pdf[0]->value(direction) + 0.5f * m_pdf[1]->value(direction);
    }

    virtual Vector3D generate() const
    {
        if(drand48() < 0.5f)
            return m_pdf[0]->generate();
        else
            return m_pdf[1]->generate();
    }
};

  对于多个光源的直接采样，我们采取均匀随机的策略，那么PDF值也应该是这些直接光源采样概率密度函数的平均值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
float HitableList::pdfValue(const Vector3D &o, const Vector3D &v) const
{
    float weight = 1.0f / m_list.size();
    float sum = 0;
    for(int x = 0;x < m_list.size();++ x)
        sum += m_list[x]->pdfValue(o, v);
    return sum * weight;
}

Vector3D HitableList::random(const Vector3D &o) const
{
    int index = static_cast<int>(drand48() * m_list.size());
    return m_list[index]->random(o);
}

  最后在光线追踪递归函数中加上我们的复合重要性采样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
Vector4D Tracer::tracing(const Ray &r, Hitable *world, Hitable *light, int depth)
{
    HitRecord rec;
    if (world->hit(r, 0.001f, FLT_MAX, rec))
    {
        ......
        if (depth < m_config.m_maxDepth && material->scatter(r, rec, srec))
        {
            if(srec.m_isSpecular)
            {
                return srec.m_attenuation * tracing(srec.m_scatterRay, world, light, depth + 1);
            }
            else
            {
                Vector3D dir;
                float pdf_val;
                if(!m_samplingList.isEmpty())
                {
                    HitablePDF light_pdf(light, rec.m_position);
                    MixturePDF mix_pdf(&light_pdf, srec.m_pdf.get());
                    dir = mix_pdf.generate();
                    pdf_val = mix_pdf.value(dir);
                }
                else
                {
                    dir = srec.m_pdf->generate();
                    pdf_val = srec.m_pdf->value(dir);
                }
                Ray scattered = Ray(rec.m_position, dir);

                return emitted + srec.m_attenuation * material->scattering_pdf(r, rec, scattered)
                        * tracing(scattered, world, light, depth + 1) / pdf_val;
            }
        }
        else
            return emitted;
    }
    else
    {
        // background color.
        ......
    }
}

程序效果

ret1

ret2

ret3

ret4

ret5

ret6

ret7

ret8

header

参考资料

$[1$ http://www.thegibook.com/

$[2]$ Peter Shirley. Ray Tracing in One Weekend. Amazon Digital Services LLC, January 26, 2016.

$[3]$ https://software.intel.com/en-us/node/506045?_ga=2.114625223.1582767698.1558613799-2057498546.1558613799

$[4]$ https://blog.csdn.net/zoufeiyy/article/details/1887579

$[5]$ https://www.jianshu.com/p/b570b1ba92bb

$[6]$ https://blog.csdn.net/libing_zeng/article/details/74989755

$[7]$ https://www.qiujiawei.com/solid-angle/

 上一页

Computer Graphics Fluid Simulation Position Based Dynamics

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 ， 总访问量为 次 。
载入天数...载入时分秒...