流体模拟Fluid Simulation：Position Based Fluid

本篇文章主要是关于Position Based Dynamics的流体模拟方法，这类方法依旧采用基于拉格朗日的视角，把流体看成由一个一个粒子组成，易于并行化，适用于实时的流体模拟。目前实现的只是CPU版本，考虑在后面利用cuda挪到GPU上做模拟计算。相关的完整代码请看这里。

• 基于位置动力学的物理模拟
• 基于位置动力学的流体模拟
• 流体模拟算法实现
• 实现效果
• 参考资料

一、基于位置动力学的物理模拟

  传统的物理模拟方法都是基于力的方法，这类方法通过计算内部力（如流体内部的粘性力、压力）和外部力（如重力和碰撞力）的合力，然后根据牛顿第二定律计算出加速度，最后根据数值计算方法求出物体的速度和位置。这种方法基本上针对每一种动态物体，会由一个独立的求解器，各种求解器按照一定的顺序计算，从而得到模拟的结果，这样会带来大量冗余的工作。基于位置动力学（Position Based Dynamics）的方法将这些物理运动通过约束表达出来，这样只需要一个求解器即可，更加方便地进行物理模拟。

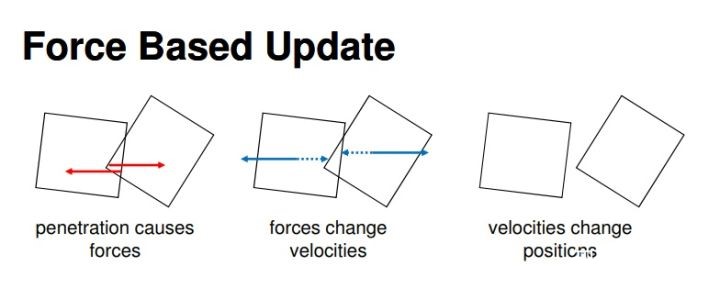
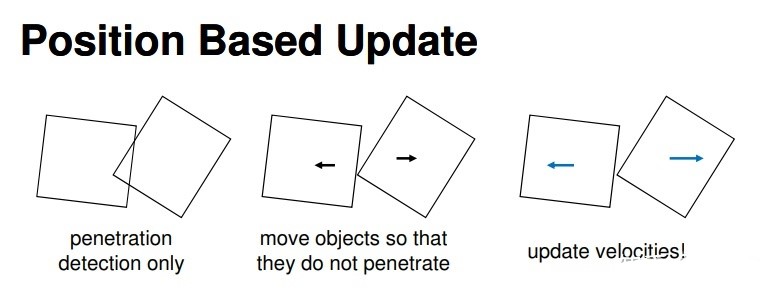
  下图1是基于力和基于位置动力学的物体碰撞更新过程的对比，可以看到基于力的碰撞检测首先在穿透发生时更新物体的速度，然后更新物体的位置。而基于位置动力学的碰撞检测首先只检测是否发生穿透，然后移动位置使之不发生穿透，最后再据此更新物体的速度信息。

图1 两种碰撞更新过程对比

1、基于位置动力学的模拟算法

  基于位置动力学英文全称为Position Based Dynamics，以下简称为PBD。接下来我们介绍经典的PBD算法。在PBD算法中，运动的物体由$N$个顶点和$M$个约束组成。顶点$i\in [1,…,N]$的质量为$m_i$，位置为$x_i$，速度为$v_i$，每个约束$j\in [1,…,M]$有如下五个性质：

• 约束的基数为$n_j$，即第$j$个约束所影响的顶点数目为$n_j$个；
• 约束函数$C_j:\ R^{3n_j}\to R$；
• 受约束影响的顶点索引值集合$\{i_1,…,i_{n_j}\},i_k\in [1,…N]$；
• 每个约束都有对应的刚度参数$k_j\in [0,1]$，这里我们可以理解为约束的强度；
• 约束分为两种，一类是等式约束即$C_j(x_{i1},x_{i_2},…,x_{i_{n_j}})=0$，另一类是不等式约束$C_j(x_{i_1},x_{i_2},…,x_{i_{n_j}})\geq 0$。

  给定时间步长$\Delta t$，PBD的运动物体模拟的算法伪代码如下所示：

$$\begin{align} &1.forall\ \ vertices\ \ i:\\ &2.\ \ \ \ initialize\ \ x_i=x_i^0,v_i=v_i^0,w_i=1/m_i\\ &3.endfor\\ &4.loop\\ &5.\ \ \ \ forall\ \ vertices\ \ i\ \ do\ \ v_i\leftarrow v_i+\Delta tw_if_{ext}(x_i)\\ &6.\ \ \ \ dampVelocities(v_1,...,v_N)\\ &7.\ \ \ \ forall\ \ vertices\ \ i\ \ do\ \ p_i\leftarrow x_i+\Delta t v_i\\ &8.\ \ \ \ forall\ \ vertices\ \ i\ \ do\ \ generateCollisionConstraints(x_i\to p_i)\\ &9.\ \ \ \ loop\ \ solverIterations\ \ times\\ &10.\ \ \ \ \ \ \ \ projectConstraints(C1,...,C_{M+M_{coll}},p_1,...,p_N)\\ &11.\ \ \ endloop\\ &12.\ \ \ forall\ \ vertices\ \ i\\ &13.\ \ \ \ \ \ \ \ v_i\leftarrow (p_i-x_i)\Delta t\\ &14.\ \ \ \ \ \ \ \ x_i\leftarrow p_i\\ &15.\ \ \ endfor\\ &16.\ \ \ velocityUpdate(v1,...,v_N)\\ &17.endloop\\ \end{align}$$

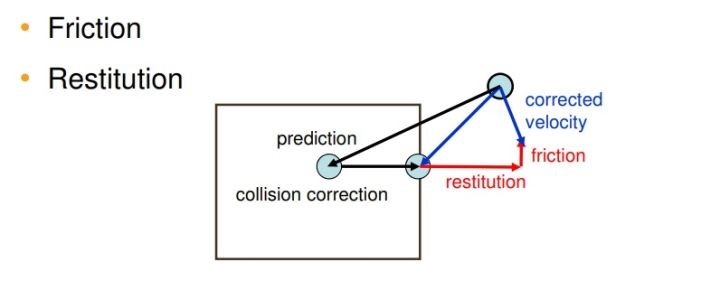
  在上面的算法第1步到第3步中，我们首先对顶点的位置、速度和质量倒数进行初始化，其中质量的倒数$w_i=1/m_i$，除了可以避免冗余的除法操作外，还可以使用于静态的物体，对于静态的物体我们设为$w_i=0$，这样在后续的更新中都不会产生位置和速度的变化量。第5步中的$f_{ext}$代表不能转换成约束形式的力（如重力），我们根据$f_{ext}$进行一次数值计算预测在$f_{ext}$的作用下的速度$v_i$。紧接着在第6步中我们添加阻尼的作用，阻尼可以理解为物体在运动中发生了能量耗散，从而导致速度有所衰减。第8行主要是生成碰撞约束，物体会与周围的环境发生碰撞，例如布料落在地板上，水碰上一面墙等，这些碰撞约束在每个时间步长都发生改变，所以每一次都需要重新生成碰撞约束。有了内部约束（如不可压缩流体的密度约束）和外部约束（如流体与地面的碰撞约束）之后，我们需要根据这些约束做一个迭代求解，也就是上面伪代码中的第9行到第11行，这里我们称为约束投影步骤。从约束投影步骤我们得到服从给定约束的粒子位置，然后再第12行到第15行更新顶点粒子的速度和位置信息。最后在第16行根据摩擦系数（friction）和恢复系数（restitution）更新速度，如下图2所示。这样，一个完整的PBD物理模拟步骤就完成了。

图2 friction和restitution

2、约束投影步骤

  接下来我们就针对约束投影步骤详细展开相关的内容，约束投影是PBD中的最难理解的核心部分，涉及的数学内容比较多一点。设有一个基数为n（也就是前面提到的$n_j$，受到该约束影响的顶点数目或者说粒子数目）的约束，关联的粒子点为$p_1,…,p_n$，约束函数记为$C$，刚度系数（stiffness）为$k$。记$p=[p_1^T,…,p_n^T]^T$，则等式约束函数表示为：

$$C(p)=0 \tag {1}$$

  我们的目标是计算这样的一个位移偏移量$\Delta p$，使得粒子顶点在$p+\Delta p$处约束条件依然满足，即：

$$C(p+\Delta p)=0 \tag {2}$$

  对约束函数$C$做一阶泰勒展开（或者导数的定义），则可得:

$$C(p+\Delta p)\approx C(p)+\nabla_pC(p)\cdot\Delta p=0 \tag {3}$$

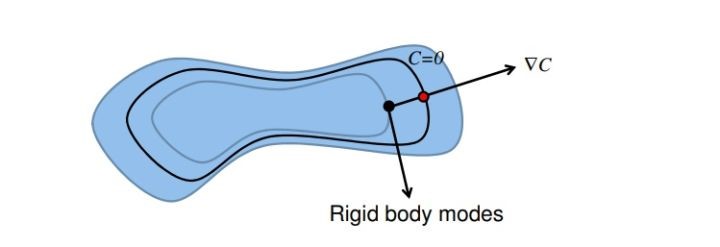
  为了使粒子在$p+\Delta p$处依然满足约束条件，我们要求解方程$(3)$得到$\Delta p$。PBD算法的一个巧妙之处在于它将$\Delta p$的方向限制在约束函数的梯度方向$\nabla_p C(p)$上。如下图3所示，约束$C$所涉及到的粒子位置会形成一个高维空间，下图为该空间中满足不同约束条件的粒子位置形成的二维等值线示意图，其中满足$C$约束条件的是黑色等值线。故当粒子处于下图的黑色点的位置时，不满足约束条件，如果我们沿着点所在的等值线（灰色曲线）移动，此时刚体模态（Rigid body modes）的方向与该等值线相同，新得到的位置仍然在该灰色等值线上，依然不在黑色曲线 $C=0$上，即不满足约束条件。这可以理解为，约束中存在的误差依然没有得到修正。以两个粒子形成的距离约束为例，就好比同时移动了两个粒子或者该约束绕自身旋转，但是存在的误差并没有得到更正。而且这样一来还会引入系统中不存在的一种外力，导致系统动量不守恒。所以，我们希望该点的位移方向与刚体模态方向垂直，从而保证系统动量守恒，即从黑点指向红点的方向$\nabla C$。

图3 约束等值线
  因此，我们令位移向量$\Delta p$为约束函数的梯度向量$\nabla_p C$再乘上一个标量缩放系数$\lambda$：

$$\Delta p=\lambda \nabla_p C(p) \tag {4}$$

  其中的标量缩放系数$\lambda$我们称之为拉格朗日乘子（Lagrange multiplier）。联立公式$(3)$和$(4)$我们可得：

$$\lambda=-\frac{C(p)}{|\nabla_pC(p)|^2} \tag {5}$$

  然后将$\lambda$再代入公式$(4)$我们可得$\Delta p$的表达式：

$$\Delta p=\lambda \nabla_pC(p)=-\frac{C(p)}{|\nabla_pC(p)|^2}\nabla_pC(p) \tag {6}$$

  具体到粒子$i$，约束投影后其对应的位移向量为：

$$\Delta p_i=-s\nabla_{p_i}C(p_1,...,p_n) \tag {7}$$

  其中的$s$为如下所示，$s$的值对于约束函数$C$作用范围内的所有点都一样。

$$s=\frac{C(p_1,...,p_n)}{\Sigma_j|\nabla_{p_j}C(p_1,...,p_n)|^2} \tag {8}$$

  前面我们假定所有的粒子质量都相同，现在考虑粒子质量不同的情况。记粒子$i$的质量为$m_i$，其质量的倒数为$w_i=1/m_i$，则公式$(4)$变为：

$$\Delta p_i=\lambda w_i\nabla_{p_i}C(p) \tag {9}$$

  公式$(7)$和公式$(8)$变为：

$$\Delta p_i=-s w_i\nabla_{p_i}C(p_1,...,p_n) \tag {10}$$ $$s=\frac{C(p_1,...,p_n)}{\Sigma_jw_j|\nabla_{p_j}C(p_1,...,p_n)|^2} \tag {11}$$

  为了便于理解，接下来我们举个简单的例子应用约束投影方法。如下图4所示。

图4 简单的约束例子
  上面的约束可以表示为$C(p_1,p_2)=|p_1-p_2|-d$，位移向量记为$\Delta p_i$。根据约束投影方法，我们首先约束函数$C(p_1,p_2)$关于$p_1$和$p_2$的梯度，也就是求偏导数。注意到$C(p_1,p_2)=|p_1-p_2|-d=(\sqrt{(p_1-p_2)^2})-d$，我们可以求得以下的梯度向量表达式：

$$\nabla_{p_1}C(p_1,p_2)=\frac{p_1-p_2}{|p_1-p_2|}\\ \nabla_{p_2}C(p_1,p_2)=-\frac{p_1-p_2}{|p_1-p_2|} \tag {12}$$

  注意，上面求到的是一个矢量，也就是我们说的梯度向量。将公式$(12)$代入公式$(11)$可得：

$$\begin{align} s=&\frac{C(p_1,...,p_n)}{\Sigma_jw_j|\nabla_{p_j}C(p_1,...,p_n)|^2}\\ =&\frac{|p_1-p_2|-d}{w_1|\nabla_{p_1}C(p_1,p_2)|^2+w_2|\nabla_{p_2}C(p_1,p_2)|^2}\\ =&\frac{|p_1-p_2|-d}{w_1+w_2} \tag {13} \end{align}$$

  最后，将公式$(13)$代入到公式$(10)$，可得约束投影计算得到的位移：

$$\begin{align} \Delta p_1=&-\frac{|p_1-p_2|-d}{w_1+w_2}w_1\nabla_{p_1}C(p_1,p_2)\\ =&-\frac{w_1}{w_1+w_2}(|p_1-p_2|-d)\frac{p_1-p_2}{|p_1-p_2|} \end{align}$$

  同理$\Delta p_2$如下所示：

$$\Delta p_2=+\frac{w_2}{w_1+w_2}(|p_1-p_2|-d)\frac{p_1-p_2}{|p_1-p_2|}$$

  前面我们提到每个约束都有对应的刚度系数$k$，令$k’=1-(1-k)^{1/n_s}$去乘$\Delta p$，这里$n_s$迭代之后误差为$\Delta p(1-k’)^{n_s}=\Delta p(1-k)$，与刚度系数成线性关系，而与迭代次数$n_s$无关。下一个时间步的位置如下所示：

$$p_1^{t+1}=p_1^t+k'\Delta p_1\\ p_2^{t+1}=p_2^t+k'\Delta p_2$$

3、约束投影求解器

  前面的伪代码中我们可以看到约束投影的输入为$M+M_{coll}$个约束和$N个$点的预测位置$p1,…,p_N$，所需要求解的方程组是非线性非对称方程组或不等式组（碰撞约束产生的）。约束投影步骤的主要任务就是修正预测位置使新得到的校正位置满足所有约束。但是一般情况下很难找到一个适当的$\Delta p=[\Delta p_1^T,…,\Delta p_n^T]^T$恰好使得所有的约束都能够同时得到满足，故我们通常采用迭代的方法按顺序依次对约束进行求解。

  我们可以采用非线性高斯-赛德尔（Non-Linear Gauss-Seidel，简称NGS）迭代方法。高斯赛德尔（Gauss-Sedel，简称GS）迭代方法只能求解线性方程组，NGS在依次求解德基础上，加入了约束投影求解这一非线性操作。与雅可比迭代方法（Jacobi method）不同，NGS求解器在一次迭代中对于顶点位置的修正立即被应用到下一个约束求解中，这样的好处就是显著加快了收敛速度。

  但是NGS虽然稳定且容易实现，但是该方法收敛速度依然不是很快，不宜并行化。

二、基于位置动力学的流体模拟

  前面部分主要介绍了Position Based Dynamics算法相关的内容，接下来我们就看看如何将其PBD算法应用到流体模拟当中，主要是如何针对流体的物理特性构建相应的约束函数。基于位置动力学的流体全称为Position Based Fluid，简称PBF。

1、不可压缩约束

  在不可压缩性的流体模拟中，我们需要使粒子$i$的密度$\rho_i$尽量与静态的密度$\rho_0$相同，即$\rho_i=\rho_0$。因此，我们需要对每一个流体粒子都施加一个常量密度约束，PBF的常量密度约束如下所示：

$$C_i(p_1,...,p_n)=\frac{\rho_i}{\rho_0}-1 \tag {14}$$

  公式$(14)$中，我们记粒子$i$的位置为$p_i$，$p_1,…,p_n$是与粒子$i$相邻的粒子。可以看到当密度约束$C_i(p_1,…,p_n)=0$时有$\rho_i=\rho_0$，此时流体的体积即不压缩也不膨胀，从而保证了流体的不可压缩条件，这就是公式$(14)$的由来。流体粒子$i$的密度根据SPH（Smoothed Particle Hydrodynamics，光滑粒子流体动力学，简称SPH）方法的计算公式如下所示：

$$\rho_i=\Sigma_jm_jW(p_i-p_j,h) \tag {15}$$

  在公式$(15)$中，$m_j$是邻居粒子$j$的质量，$h$是指定的光滑核半径。$W$函数我们接下来会提到。将公式$(15)$代入公式$(14)$，我们有：

$$C_i(p_1,...,p_n)=\frac{\Sigma_j m_jW(p_i-p_j,h)}{\rho_0}-1 \tag {16}$$

  在公式$(15)$的密度计算中，PBF方法采用了Poly6核函数：

$$W_{poly6}(r,h)=\frac{315}{64\pi h^9} \begin{cases} (h^2-|r|^2)^3\ \ \ \ 0\leq|r|\leq h\\ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ otherwise \end{cases} \tag {17}$$

  但是在计算密度的梯度时，却又采用了Spiky核函数：

$$W_{spiky}(r,h)=\frac{15}{\pi h^6} \begin{cases} (h-|r|)^3\ \ \ \ 0\leq|r|\leq h\\ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0therwise \end{cases} \tag {18}$$

  对公式$(18)$求关于$r$的导数（注意，$|r|=\sqrt{r^2}$，不能直接对$|r|$求导），从而流体粒子密度的梯度如下所示：

$$\nabla W_{spiky}(r,h)=-\frac{45}{\pi h^6} \begin{cases} (h-|r|)^2\frac{r}{|r|}\ \ \ \ 0\leq|r|\leq h\\ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ otherwise \end{cases} \tag {19}$$

  因此，粒子$i$的约束函数$(16)$是一个关于$p_1,…,p_n$的非线性方程组$C_i(p_1,…,p_n)=0$，所有粒子$i$的约束组成了一个非线性方程组。在PBF方法中，我们只考虑粒子质量相同的情况，故我们可以省去公式$(15)$和公式$(16)$中的质量$m_j$，即：

$$\rho_i=\Sigma_jW(p_i-p_j,h) \tag {20}$$ $$C_i(p_1,...,p_n)=\frac{\Sigma_j W(p_i-p_j,h)}{\rho_0}-1 \tag {21}$$

  然后求约束函数$C_i$关于$p_k$的梯度如下，其中$k\in\{1,2,…,n\}$：

$$\nabla_{p_k}C_i=\frac1\rho_0\Sigma_j\nabla_{p_k}W(p_i-p_j,h) \tag {22}$$

  显然，针对$k$的不同，分为两种情况。当$k=i$也就是粒子本身的时候，连加符号中的$W$均为关于$p_k$的函数；当$k=j$即邻居粒子的时候，只有$W(p_i-p_k,h)$才有意义，其他相对于$p_k$来说都是常量，故导数为0（注意用到了求导的链式法则）：

$$\nabla_{p_k}C_i=\frac1\rho_0 \begin{cases} \Sigma_j\nabla_{p_k}W(p_i-p_j,h)\ \ \ \ if\ \ k=i\\ -\nabla_{p_k}W(p_i-p_j,h)\ \ \ \ \ if\ \ k=j \end{cases} \tag {23}$$

  既然求出了约束函数的梯度，我们就把它应用到前面提到的拉格朗日乘子的计算公式中，联立公式$(5)$和公式$(23)$，我们有：

$$\lambda_i=-\frac{C_i(p_1,...,p_n)}{\Sigma_k|\nabla_{p_k}C_i|^2} \tag {24}$$

2、混合约束

  如果一个约束条件不能被违背，我们称之为硬约束；而能一定程度上被违背的约束称为软约束。在理想的情况下，我们都希望约束始终是硬约束，但是由于误差或者数值方法的不稳定等原因，我们有时不得不向软约束妥协。

  在PBF中，当$|r|=h$，粒子$i$与粒子$j$之间的距离等于光滑核半径时，粒子$i$和粒子$j$处于即将分离的状态。注意观察公式$(19)$的密度梯度计算公式，此时$\nabla W_{spiky}(r,h)=0$。若所有的邻居粒子与粒子$i$都处于这种状态，那么必将导致约束函数的梯度即公式$(22)$取值为0：

$$\nabla_{p_k}C_i=\frac1\rho_0\Sigma_j\nabla_{p_k}W(p_i-p_j,h) = 0$$

  从而导致公式$(24)$中的分母$\Sigma_k|\nabla_{p_k}C_i|^2$为0，出现除零错误，这将导致PBF方法出现潜在的不稳定性。为了解决这个问题，PBF采用混合约束的方法，使密度硬约束转变成软约束。具体的做法就是将根据密度函数求解得到的约束力再加入到原始的约束函数中，这里在PBF的常量密度约束中得到的拉格朗日乘子$\lambda$有类似的作用，故将$\lambda$加入到初始的约束方程（即公式$(3)$）：

$$C(p+\Delta p)\approx C(p)+\nabla C^T\nabla C \lambda + \epsilon\lambda=0 \tag {25}$$

  公式$(25)$中的$\epsilon$是松弛参数，可以由用户指定。引入公式$(25)$后，拉格朗日乘子的计算公式$(24)$就变为：

$$\lambda_i=-\frac{C_i(p_1,...,p_n)}{\Sigma_k|\nabla_{p_k}C_i|^2+\epsilon} \tag {26}$$

  从而可得粒子$i$在经过上述约束投影后对应的位移向量（包括自身密度约束以及邻居粒子密度约束共同作用的结果。注意，这里对应的上面的公式$(4)$，结合公式$(23)$）：

$$\begin{align} \Delta p_i&=\lambda_i \nabla_{p_i}C_i+\Sigma_j\lambda_j\nabla_{p_j}C_i\\ &=\frac1\rho_0\Sigma_j\lambda_i\nabla_{p_i}W(r,h)+(-\frac1\rho_0\Sigma_j\lambda_j\nabla_{p_j}W(r,h))\\ &=\frac1\rho_0\Sigma_j\lambda_i\nabla_{p_i}W(r,h)+\frac1\rho_0\Sigma_j\lambda_j\nabla_{p_i}W(r,h)\\ &=\frac{1}{\rho_0}\Sigma_j(\lambda_i+\lambda_j)\nabla_{p_i}W(r,h) \end{align} \tag {27}$$

3、拉伸不稳定性

  PBF采用SPH的方法来计算流体粒子的密度，但是该方法通常需要30~40个邻居粒子才能使密度求值结果趋于静态密度。在邻居粒子数量较少的情况下，通过该方法计算得到的流体密度低于静态密度，由此会造成流体内部压强为负数，原本粒子间的压力变为吸引力，使得流体粒子凝聚在一起，导致流体表面的模拟效果失真。PBF采用了一种人工排斥力的计算模型，当流体粒子距离过近时该排斥力会使它们分开，避免产生粒子聚集的现象。在公式$(24)$的基础上，加入一个排斥项（repulsive term）$s_{corr}$：

$$\Delta p_i=\frac1\rho_0\Sigma_j(\lambda_i+\lambda_j+s_{corr})\nabla_{p_i}W(p_i-p_j,h) \tag {28}$$

  其中的$s_{corr}$计算方式如下：

$$s_{corr}=-k(\frac{W(p_i-p_j,h)}{W(\Delta q,h)})^n \tag {29}$$

  公式$(29)$中，$\Delta q$表示到粒子$i$的一个固定距离，通常取$|\Delta q|=0.1h,…,0.3h$，$h$即前面提到的光滑核半径。此外，公式中的$k$可以看作表面张力参数，取值$k=0.1$，而$n=4$。公式$(28)$中的排斥项会使得流体粒子的密度稍微低于静态密度，从而产生类似于表面张力的效果，使得流体表面的的粒子分布均匀。通过这个排斥项，我们不再需要硬性规定流体的邻居数量必须在30~40个，进一步提升算法的流体模拟效率。

4、涡轮控制和人工粘性

  由于数值耗散，PBD的方法会引入额外的阻尼，使得整个系统的能量损耗太快，导致本来应该由的一些涡流细节迅速消失。在这里，PBF通过涡轮控制方法向整个系统重新注入能量：

$$f_i^{vorticity}=\epsilon (N\times \omega_i) \tag {30}$$

  上述的公式中，$N=\frac{\eta}{|\eta|},\ \eta=\nabla|\omega|_i$，而流体粒子的旋度$\omega_i$计算公式如下：

$$\omega_i=\nabla\times v=\Sigma_j(v_j-v_i)\times \nabla_{p_j}W(p_i-p_j,h) \tag {31}$$

  涡轮控制方法的基本思路就是：通过添加一个体积力$f_i^{vorticity}$（在算法的第一步），在旋度粒子（可直观理解为比周围粒子旋转快的粒子，旋度$\omega_i$指向粒子$i$的旋转轴）处加速粒子的旋转运动，通过这种方式来增加系统的旋度细节。公式$(30)$中的$\epsilon$用于控制涡轮控制力的强度。

  最后，PBF方法采用XSPH的粘度方法直接更新速度，从而产生粘性阻尼。人工粘性除了可以增加模拟的数值稳定性，还可以消除非物理的流体振荡。拉格朗日流体模拟方法中，人工粘性本质上会对流体粒子的相对运动产生阻尼作用，使流体的动能转化为热能：

$$v_i^{new}=v_i+c\Sigma_j(v_i-v_j)\cdot W(p_i-p_j,h) \tag {32}$$

  在流体模拟中，我们取公式$(32)$中的$c=0.01$。

5、PBF算法

  PBF算法的总体框架就是按照前面提到的PBD算法，只是经典PBD算法采用了顺序高斯-赛德尔（Sequential Gauss-Seidel，SGS）迭代求解，而SGS不容易被GPU并行化，因此基于CUDA实现的PBF求解器使用了雅克比（Jacobi）迭代方法并行求解。

  PBF的算法伪代码如下所示：

$$\begin{align} &1.\ forall\ \ particles\ \ i\ \ do\\ &2.\ \ \ \ \ apply\ \ force\ \ v_i\leftarrow v_i+\Delta tf_{ext}(x_i)\\ &3.\ \ \ \ \ predict\ \ position\ \ x_i^*\leftarrow x_i+\Delta t v_i\\ &4.\ endfor\\ &5.\ forall\ \ particles\ \ i\ \ do\\ &6.\ \ \ \ \ find\ \ neighboring\ \ particles\ \ N_i(x_i^*)\\ &7.\ endfor\\ &8.\ while\ \ iter\ \ <\ \ solverIterations\ \ do\\ &9.\ \ \ \ \ forall\ \ particles\ \ i\ \ do\\ &10.\ \ \ \ \ \ \ \ calculate\ \ \lambda_i\\\ &11.\ \ \ \ endfor\\ &12.\ \ \ \ forall\ \ particles\ \ i\ \ do\\ &13.\ \ \ \ \ \ \ \ calculate\ \ \Delta p_i\\ &14.\ \ \ \ \ \ \ \ perform\ \ collision\ \ detection\ \ and\ \ response\\ &15.\ \ \ \ endfor\\ &16.\ \ \ \ forall\ \ particles\ \ i\ \ do\\ &17.\ \ \ \ \ \ \ \ update\ \ position\ \ x_i^*\leftarrow x_i^*+\Delta p_i\\ &18.\ \ \ \ endfor\\ &19.endwhile\\ &20.forall\ \ particles\ \ i\ \ do\\ &21.\ \ \ \ update\ \ velocity\ \ v_i\leftarrow\frac1{\Delta t}(x_i^*-x_i)\\ &22.\ \ \ \ apply\ \ vorticity\ \ confinement\ \ and\ \ XSPH\ \ viscosity\\ &23.\ \ \ \ update\ \ position\ \ x_i\leftarrow x_i^*\\ &24.endfor \end{align}$$

三、流体模拟算法实现

  在前面的理论讨论部分我们没有提到流体与固体边界的交互作用，实际上这对于流体模拟来说是非常重要，一般丰富的流体细节都要通过与刚体、软体以及其他流体的相互作用表现出来，目前我们仅考虑流体与刚体的交互效果。一般做刚体碰撞都是采用的射线与三角形求交，检测是否发生了穿透，然后根据交点修正物体的位置，从而表现出碰撞反弹的效果。这里我们并不采用这种方法，而是采用像流体一样的表示方法，将固体用一个一个粒子表示，流体与刚体的碰撞通过流体粒子与刚体粒子的属性作用间接地表现出来。这种方法非常自然，可以对任意形状的物体做碰撞， 只要将刚体表示成粒子表示，非常适用于在GPU上实现，当然缺点就是增大了内存开销。

  加入了刚体边界粒子，在计算密度、拉格朗日乘子、流体密度约束的时候，我们就需要考虑刚体粒子对流体粒子这些属性的贡献。在计算流体密度时，公式变成如下：

$$\rho_i=\Sigma_jm_jW(x_i-x_j,h)+\Sigma_k\phi_{b_k}W(x_i-x_k,h) \tag {33}$$

  可以看到，除了邻居的流体粒子，还加入了刚体刚体粒子的属性计算，即公式最右边的那一项，其中$\phi_{b_k}$计算如下：

$$\phi_{b_k}=\rho_0\frac{m_{b_k}}{\Sigma_lm_{b_l}W(x_k-x_l,h)} \tag {34}$$

  对于流体粒子，我们可以把$\phi_{b_k}$看成是刚体粒子的质量，对于每一个固体粒子$b_k$，我们可以提前计算好它的$\phi_{b_k}$值，避免每一步的模拟都重新计算。同样地，计算拉格朗日乘子也要考虑刚体粒子的作用：

$$\lambda_i=-\frac{C_i(p_1,...,p_n)}{\Sigma_k|\nabla_{p_k}C_i|^2+\Sigma_l|\nabla_{p_l}C_i|^2+\epsilon}$$

  最后，在做密度约束投影时，加入刚体粒子的贡献：

$$\Delta p_i=\frac{1}{\rho_0}\Sigma_j(\lambda_i+\lambda_j)\nabla_{p_i}W(r,h) +\frac{1}{\rho_0}\Sigma_k\lambda_i\nabla_{p_i}W(r,h) \tag {35}$$

  因为刚体粒子并没有流体的拉格朗日乘子，所以公式$(35)$中的刚体粒子项没有加上刚体粒子的拉格朗日乘子。接下来就是流体模拟算法的实现细节叙述，多线程库我采用了tbb。

1、三次样条核函数

  在计算流体密度时及其梯度时，我采用三次样条核函数：

$$W(r,h)= \begin{cases} \frac8{\pi h^3}(6\frac{|r|^3}{h^3}-6\frac{|r|^2}{h^2}+1)\\ \frac{16}{\pi h^3}(1-\frac{|r|}{h})^3 \end{cases} \tag {36}$$

  相应地，其梯度为：

$$\nabla W(r,h)= \begin{cases} \frac{48}{\pi h^3}(3(\frac{|r|}{h})^2-2(\frac{|r|}{h}))\frac{r}{h\cdot|r|}\\ \frac{48}{\pi h^3}(1-\frac{|r|}{h})^2(-\frac{r}{h|r|}) \end{cases} \tag {37}$$

  故核函数的计算代码如下所示：

real SPHKernels::poly6WKernel(const glm::vec3 & r)
{
	real ret = 0.0;
	real rl = glm::length(r);
	real q = rl / m_radius;
	real h3 = m_radius * m_radius * m_radius;
	if (q <= 0.5)
	{
		real q2 = q * q;
		real q3 = q2 * q;
		ret = 8.0 / (M_PI * h3) * (6.0 * q3 - 6.0 * q2 + 1.0);
	}
	else
	{
		ret = 16.0 / (M_PI * h3) * pow(1 - q, 3.0);
	}
	return ret;
}
glm::vec3 SPHKernels::spikyWKernelGrad(const glm::vec3 & r)
{
	glm::vec3 ret(0.0f);
	real rl = glm::length(r);
	real q = rl / m_radius;
	real h3 = m_radius * m_radius * m_radius;
	if (rl > 1.0e-6)
	{
		const glm::vec3 gradq = static_cast<float>(1.0 / (rl * m_radius)) * r;
		if (q <= 0.5)
		{
			ret = static_cast<float>(48.0 / (M_PI * h3) * q * (3.0 * q - 2.0)) * gradq;
		}
		else
		{
			real factor = 1.0 - q;
			ret = static_cast<float>(48.0 / (M_PI * h3) * (-factor * factor)) * gradq;
		}
	}
	return ret;
}

2、粒子表示

  在实现时，除了流体粒子，我们还要存储刚体粒子，但是刚体粒子又跟流体粒子稍微有点不同。刚体粒子的属性不需要每次重新计算，为此，我采用的方法是将流体粒子和刚体粒子统一存储，流体粒子在前面部分，刚体粒子在后面部分，这样可以通过索引下标判断当前是哪种粒子。

  对于每一个粒子，我们需要存储它的质量、当前位置、上一次位置、静止时的位置、速度、加速度。

class ParticleGroup
{
private:
	std::vector<real> m_masses;
	std::vector<real> m_invMasses;
	std::vector<glm::vec3> m_position;
	std::vector<glm::vec3> m_velocity;
	std::vector<glm::vec3> m_oldPosition;
	std::vector<glm::vec3> m_restPosition;
	std::vector<glm::vec3> m_lastPosition;
	std::vector<glm::vec3> m_acceleration;

public:
	.....
};

3、粒子领域搜索

  由前面的算法伪代码可以看到，在做流体约束投影之前，我们需要首先搜索每个粒子的邻居粒子。最简单暴力的方法是直接遍历每一个粒子，判断每一个粒子是否与当前的粒子相邻，这种算法的复杂度为$O(n^2)$（即对每一个粒子都要遍历$n$次），随着粒子数量的增多，搜索时间迅速增长。为此，我参考了InteractiveComputerGraphics的开源代码，采用一种空间哈希的算法，将算法的复杂度降低到$O(n)$。

  每一个粒子都有它的位置向量$(x,y,z)$，我们将空间做一个网格分割，每个网格单元是边长为$e$的立方体，这样可以将整个三维空间都看成由一个一个网格单元的立方体构成（其实就是三维网格），每个单元按照立方体顶点位置最小的那个点做一个编号。那么如何知道每个粒子落在哪个网格呢？只需将粒子的位置向量除以网格单元边长即可，$(x/e,y/e,z/e)$就是粒子所在单元的编号，接下来有两种做法：一种就是根据$(x/e,y/e,z/e)$做一个随机哈希映射得到哈希索引值，将该粒子存储到哈希索引值指向的一个线性表；另一种方法是根据$(x/e,y/e,z/e)$直接按照某一个顺序存储到线性表中。显然前者会产生哈希冲突，故需要考虑冲突处理，这里我直接采用拉链法；而后者需要申请的存储空间依赖于包围盒的大小，而且一般情况下很多的存储空间都是没有粒子的。目前我采用前者的方法。每次我们存储到线性表中的是粒子的下标索引，避免大量的内存拷贝，因为这很耗时。

  将每个粒子映射到一个线性表之后，我们就根据这个线性表获取每个粒子的邻居，此时我们只需查看粒子所在网格周围的$3\times 3\times 3=27$个网格，算法复杂度变为$O(27*n)=O(n)$。可以看到，这个算法思想很简单，而且效率很高。算法分成两个步骤，分别是粒子映射、邻域搜索。

void NeighborSearch::neighborhoodSearch(const std::vector<glm::vec3>& particles,
	const unsigned int &start, const unsigned int &num)
{
	const real factor = 1.0 / m_cellGridSize;
	unsigned int numParticles = particles.size();
	m_neighbors.assign(numParticles, std::vector<unsigned int>());
	// hash mapping.
	for (unsigned int x = 0; x < numParticles; ++x)
	{
		glm::ivec3 cellPos;
		cellPos.x = floor(particles[x].x * factor) + 1;
		cellPos.y = floor(particles[x].y * factor) + 1;
		cellPos.z = floor(particles[x].z * factor) + 1;
		SpatialCell *&entry = m_spatialMap[&cellPos];

		if (entry != nullptr)
		{
			if (entry->m_timeStamp != m_currentTimestamp)
			{
				entry->m_timeStamp = m_currentTimestamp;
				entry->m_particleIndices.clear();
			}
		}
		else
		{
			SpatialCell *newEntry = new SpatialCell();
			newEntry->m_particleIndices.reserve(m_maxParticlesPerCell);
			newEntry->m_timeStamp = m_currentTimestamp;
			entry = newEntry;
		}
		entry->m_particleIndices.push_back(x);
	}

	// hash lookup.
	unsigned int end = start + num;
	parallel_for(blocked_range<size_t>(start, end, 5000),
		[&](blocked_range<size_t> &r)
	{
		for (size_t x = r.begin(); x != r.end(); ++x)
		{
			const int cellPos1 = floor(particles[x].x * factor);
			const int cellPos2 = floor(particles[x].y * factor);
			const int cellPos3 = floor(particles[x].z * factor);
			for (unsigned char i = 0; i < 3; ++i)
			{
				for (unsigned char j = 0; j < 3; ++j)
				{
					for (unsigned char k = 0; k < 3; ++k)
					{
						glm::ivec3 cellPos(cellPos1 + i, cellPos2 + j, cellPos3 + k);
						SpatialCell * const *entry = m_spatialMap.query(&cellPos);
						if ((entry != nullptr) && (*entry != nullptr) &&
							((*entry)->m_timeStamp == m_currentTimestamp))
						{
							for (unsigned int m = 0; m < (*entry)->m_particleIndices.size(); ++m)
							{
								const unsigned int index = (*entry)->m_particleIndices[m];
								// not consider itself.
								if (index != x)
								{
									const real dist = glm::length(particles[x] - particles[index]);
									if (dist < m_radius)
									{
										m_neighbors[x].push_back(index);
									}
								}
							}
						}
					}
				}
			}
		}
	}
	);
}

  注意，对于每个邻居网格的粒子我们还要判断一下目标粒子和当前粒子的距离，超过光滑核函数的半径不视为邻居粒子。采用的哈希映射函数如下所示：

template<>
inline unsigned int hashFunction<glm::ivec3*>(glm::ivec3* const &key)
{
	const int p1 = 73856093 * key->x;
	const int p2 = 19349663 * key->y;
	const int p3 = 83492791 * key->z;
	return p1 + p2 + p3;
}

4、密度计算

  根据前面我们提到的考虑了刚体粒子的密度公式$(33)$，密度计算的代码如下所示。注意neighbors并不包含自己在内，还要在最开始加入自己的密度。比较简单，不再赘述。

bool PositionBasedFluids::computeFluidDensity(
	const unsigned int& particleIndex,
	const unsigned int& numFluidParticle,
	const std::vector<glm::vec3>& position,
	const std::vector<real>& mass,
	const std::vector<unsigned int>& neighbors,
	const real & density0,
	real & density_err,
	real & density)
{
	density = mass[particleIndex] * SPHKernels::getZeroWKenel();
	for (unsigned int x = 0; x < neighbors.size(); ++x)
	{
		unsigned int neighborIndex = neighbors[x];
		if (neighborIndex < numFluidParticle)
		{
			density += mass[neighborIndex] * SPHKernels::poly6WKernel(
				position[particleIndex] - position[neighborIndex]);
		}
		else
		{
			density += mass[neighborIndex] * SPHKernels::poly6WKernel(
				position[particleIndex] - position[neighborIndex]);
		}
	}
	density_err = std::max(density, density0) - density0;
	return true;
}

  上面的流体密度计算过程中，将会用到刚体粒子的质量值，也就是前面提到的公式$(34)$，不需要每一步重新生成，只需初始时预先计算好即可。注意公式$(34)$的计算只涉及到刚体粒子。

// calculate boundary's properties.
NeighborSearch neighborhood(nBoundaryParticles, m_sphRadius);
neighborhood.neighborhoodSearch(boundaryParticles, 0, nBoundaryParticles);
parallel_for(blocked_range<size_t>(0, nBoundaryParticles, 5000),
	[&](blocked_range<size_t> &r)
{
	for (size_t x = r.begin(); x != r.end(); ++x)
	{
		std::vector<unsigned int> &neighbors = neighborhood.getNeighbors(x);
		real delta = SPHKernels::getZeroWKenel();
		for (unsigned int y = 0; y < neighbors.size(); ++y)
		{
			unsigned int neighborIndex = neighbors[y];
			delta += SPHKernels::poly6WKernel(boundaryParticles[x] 
				- boundaryParticles[neighborIndex]);
		}
		delta = m_density0 / delta;
		m_particles.setMass(x + nFluidPartiles, delta);
	}
}
);

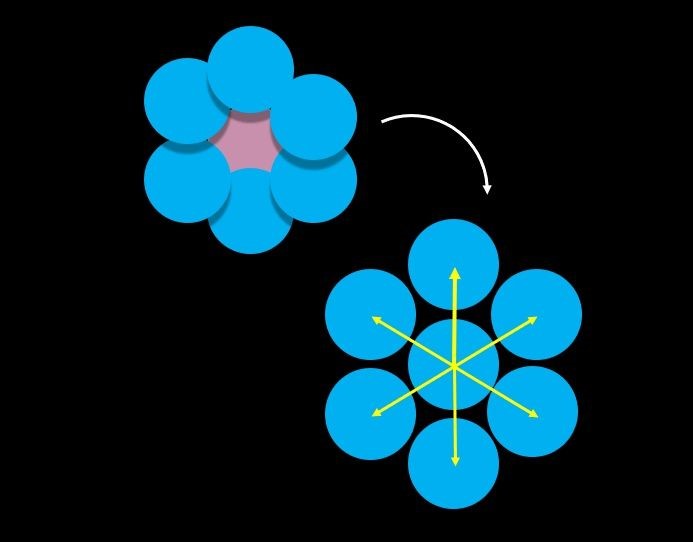
5、拉格朗日乘子计算

  前面我们在讨论PBF的约束时，采用了等式约束，也就是$C_i(p_1,…,p_n)=0$，当不等于0时我们就做约束投影进行位移修正。但当$C_i(p_1,…,p_n)<0$即$\rho_i<\rho_0$时没有必要做约束投影，这是因为当$\rho_i<\rho_0$时，粒子之间距离比较远，从而使得计算出来得密度小于静止密度。直观理解就是只有在粒子靠得比较近的（流体被压缩了）时候才需要将粒子分开，从而使流体表现出不可压缩的特性。如下图所示：

  所以我们对约束函数做了clamp操作，小于等于0一致当成等于0，具体看下面代码的第12行。

bool PositionBasedFluids::computeLagrangeMultiplier(
	const unsigned int& particleIndex,
	const unsigned int& numFluidParticle,
	const std::vector<glm::vec3>& position,
	const std::vector<real>& mass,
	const std::vector<unsigned int>& neighbors,
	const real & density,
	const real & density0,
	real & lambda)
{
	const real eps = 1.0e-6;
	const real constraint = std::max(density / density0 - 1.0, 0.0);
	if (constraint != 0.0)
	{
		real sum_grad_cj = 0.0;
		glm::vec3 grad_ci(0.0);
		for (unsigned int x = 0; x < neighbors.size(); ++x)
		{
			unsigned int neighborIndex = neighbors[x];
			if (neighborIndex < numFluidParticle)
			{
				glm::vec3 grad_cj = static_cast<float>(+mass[neighborIndex] / density0)
					* SPHKernels::spikyWKernelGrad(position[particleIndex] - position[neighborIndex]);
				sum_grad_cj += pow(glm::length(grad_cj), 2.0);
				grad_ci += grad_cj;
			}
			else
			{
				glm::vec3 grad_cj = static_cast<float>(+mass[neighborIndex] / density0)
					* SPHKernels::spikyWKernelGrad(position[particleIndex] - position[neighborIndex]);
				sum_grad_cj += pow(glm::length(grad_cj), 2.0);
				grad_ci += grad_cj;	
			}
		}
		sum_grad_cj += pow(glm::length(grad_ci), 2.0);
		lambda = -constraint / (sum_grad_cj + eps);
	}
	else
		lambda = 0.0;
	return true;
}

6、密度约束投影

  对于每一个粒子，我们根据前面计算得到的密度和拉格朗日乘子做约束投影，对应前面的公式$(35)$，密度约束投影得到的是一个用于后面做修正的位置偏移向量，从而使得粒子位移后依然满足约束条件，这就是约束投影的本质。

bool PositionBasedFluids::solveDensityConstraint(
	const unsigned int& particleIndex,
	const unsigned int& numFluidParticle,
	const std::vector<glm::vec3>& position,
	const std::vector<real>& mass,
	const std::vector<unsigned int>& neighbors,
	const std::vector<real>& lambda,
	const real &sphRadius,
	const real &density0,
	glm::vec3 &deltaPos)
{
	deltaPos = glm::vec3(0.0f);
	for (unsigned int x = 0; x < neighbors.size(); ++x)
	{
		unsigned int neighborIndex = neighbors[x];
		if (neighborIndex < numFluidParticle)
		{
			glm::vec3 grad_cj = static_cast<float>(mass[neighborIndex] / density0) 
				* SPHKernels::spikyWKernelGrad(position[particleIndex] - position[neighborIndex]);
			deltaPos += static_cast<float>(lambda[particleIndex] + lambda[neighborIndex]) * grad_cj;
		}
		else
		{
			glm::vec3 grad_cj = static_cast<float>(mass[neighborIndex] / density0)
				* SPHKernels::spikyWKernelGrad(position[particleIndex] - position[neighborIndex]);
			deltaPos += static_cast<float>(lambda[particleIndex]) * grad_cj;
		}
	}
	return true;
}

  然后我们按照算法伪代码的第8行到第19行的步骤将上述的三个步骤串联起来，迭代方法是雅可比迭代方式，按照先后顺序分别是密度计算、拉格朗日乘子计算、约束投影计算、位置修正。如下所示，在代码的第63行到第71行，我们根据约束投影计算得到的位移偏移量修正当前的粒子位置。

void FluidModelSolver::constraintProjection()
{
	unsigned int iter = 0;
	unsigned int nFluidParticles = m_lambda.size();

	while (iter < m_maxIter)
	{
		// calculate density and lagrange multiplier.
		parallel_for(blocked_range<size_t>(0, nFluidParticles, 1000),
			[&](blocked_range<size_t> &r)
		{
			for (size_t x = r.begin(); x != r.end(); ++x)
			{
				real density_err;
				std::vector<unsigned int> &neighbors = m_neighborSearch->getNeighbors(x);
				PositionBasedFluids::computeFluidDensity
				(
					x,
					nFluidParticles,
					m_particles.getPositionGroup(),
					m_particles.getMassGroup(),
					neighbors,
					m_density0,
					density_err,
					m_density[x]
				);
				PositionBasedFluids::computeLagrangeMultiplier
				(
					x,
					nFluidParticles,
					m_particles.getPositionGroup(),
					m_particles.getMassGroup(),
					neighbors,
					m_density[x],
					m_density0,
					m_lambda[x]
				);
			}
		});

		// perform density constraint.
		parallel_for(blocked_range<size_t>(0, nFluidParticles, 1000),
			[&](blocked_range<size_t> &r)
		{
			for (size_t x = r.begin(); x != r.end(); ++x)
			{
				std::vector<unsigned int> &neighbors = m_neighborSearch->getNeighbors(x);
				PositionBasedFluids::solveDensityConstraint
				(
					x,
					nFluidParticles,
					m_particles.getPositionGroup(),
					m_particles.getMassGroup(),
					neighbors,
					m_lambda,
					m_sphRadius,
					m_density0,
					m_deltaPos[x]
				);
			}
		});

		// add the delta position to particles' position.
		parallel_for(blocked_range<size_t>(0, nFluidParticles, 10000),
			[&](blocked_range<size_t> &r)
		{
			for (size_t x = r.begin(); x != r.end(); ++x)
			{
				m_particles.getPosition(x) += m_deltaPos[x];
			}
		});
		++iter;
	}
}

7、更新粒子速度

  由前面的步骤我们得到了正确的粒子位置，接下来我们根据前一帧的位置和当前的粒子位置更新每个粒子的速度向量，这样就能得到正确的粒子速度向量。计算速度是直接根据速度的定义进行的，见下面代码里的velocityUpdateFirstOrder函数，注意这种方式计算速度只有一阶精度。

	// update velocities.
	parallel_for(blocked_range<size_t>(0, nFluidParticles, 5000),
		[&](blocked_range<size_t> &r)
	{
		for (size_t x = r.begin(); x != r.end(); ++x)
		{
			PositionBasedFluids::velocityUpdateFirstOrder(
				m_timeStep,
				m_particles.getMass(x),
				m_particles.getPosition(x),
				m_particles.getOldPosition(x),
				m_particles.getVelocity(x)
			);
		}
	});

void PositionBasedFluids::velocityUpdateFirstOrder(
	const real & h, 
	const real & mass,
	const glm::vec3 & position,
	const glm::vec3 & oldPosition,
	glm::vec3 & velocity)
{
	if (mass != 0.0)
		velocity = static_cast<float>(1.0 / h) * (position - oldPosition);
}

8、旋度控制

  接下来我们给流体加上旋度细节，它的基本思路就是：通过添加一个体积力$f_i^{vorticity}$，在旋度粒子（可直观理解为比周围粒子旋转快的粒子，旋度$\omega_i$指向粒子$i$的旋转轴）处加速粒子的旋转运动，通过这种方式来增加系统的旋度细节。这个我们在前面已经讨论过，旋度控制力的计算方式如下：

$$f_i^{vorticity}=\epsilon (N\times \omega_i) \\ \omega_i=\nabla\times v=\Sigma_j(v_j-v_i)\times \nabla_{p_j}W(p_i-p_j,h) \\ N=\frac{\eta}{|\eta|},\ \eta=\nabla|\omega|_i$$

  关于这方面的内容，论文$[2]$的作者并没有作详细的说明，计算得到的旋度体积力$f_i^{vorticity}$如何作用到流体粒子上。所以我将计算得到的$f_i^{vorticity}$用于更新流体粒子的速度向量，感觉有点不太对劲，暂时先这样。代码见下面，首先计算流体的旋度向量，然后据此计算旋度体积力向量，最后给每个粒子加上在旋度体积力下的速度场偏移。代码不知道哪里有错，$\epsilon$一旦设置得有点大，整个流体就飞溅，很不正常。错误稍后再查。

void FluidModelSolver::computeVorticityConfinement()
{
	unsigned int nFluidParticles = m_lambda.size();
	static bool test = true;
	glm::vec3 record(-FLT_MAX);
	std::vector<glm::vec3> deltaVelocity(nFluidParticles, glm::vec3(0.0f));
	for (unsigned int x = 0; x < nFluidParticles; ++x)
	{
		std::vector<unsigned int> &neighbors = m_neighborSearch->getNeighbors(x);
		glm::vec3 N(0.0f);
		glm::vec3 curl(0.0f);
		glm::vec3 curlX(0.0f);
		glm::vec3 curlY(0.0f);
		glm::vec3 curlZ(0.0f);
		const glm::vec3 &velocity_i = m_particles.getVelocity(x);
		const glm::vec3 &position_i = m_particles.getPosition(x);
		for (unsigned int y = 0; y < neighbors.size(); ++y)
		{
			unsigned int neighborIndex = neighbors[y];
			if (neighborIndex >= nFluidParticles)
				continue;
			const glm::vec3 velGap = m_particles.getVelocity(neighborIndex) - velocity_i;
			curl += glm::cross(velGap, SPHKernels::spikyWKernelGrad(position_i - 
				m_particles.getPosition(neighborIndex)));
			curlX += glm::cross(velGap, SPHKernels::spikyWKernelGrad(position_i + glm::vec3(0.01, 0.0, 0.0)
				- m_particles.getPosition(neighborIndex)));
			curlY += glm::cross(velGap, SPHKernels::spikyWKernelGrad(position_i + glm::vec3(0.0, 0.01, 0.0)
				- m_particles.getPosition(neighborIndex)));
			curlZ += glm::cross(velGap, SPHKernels::spikyWKernelGrad(position_i + glm::vec3(0.0, 0.0, 0.01)
				- m_particles.getPosition(neighborIndex)));
		}
		if (glm::isnan(curl).x || glm::isnan(curl).y || glm::isnan(curl).z)
			continue;
		real curlLen = glm::length(curl);
		N.x = glm::length(curlX) - curlLen;
		N.y = glm::length(curlY) - curlLen;
		N.z = glm::length(curlZ) - curlLen;
		N = glm::normalize(N);
		if (glm::isnan(N).x || glm::isnan(N).y || glm::isnan(N).z)
			continue;
		glm::vec3 force = 0.000010f * glm::cross(N, curl);
		deltaVelocity[x] = static_cast<float>(m_timeMgr->getTimeStepSize()) * force;
	}
	for (unsigned int x = 0; x < nFluidParticles; ++x)
	{
		m_particles.getVelocity(x) += deltaVelocity[x];
	}
}

9、流体粘性

  然后就是人工粘性的计算，计算公式即前面讨论的公式$(32)$，如下所示。

$$v_i^{new}=v_i+c\Sigma_j(v_i-v_j)\cdot W(p_i-p_j,h)$$

  其中的$c$就是流体的粘性系数。

void FluidModelSolver::computeXSPHViscosity()
{
	unsigned int nFluidParticles = m_lambda.size();
	for (unsigned int x = 0; x < nFluidParticles; ++x)
	{
		glm::vec3 &velocity = m_particles.getVelocity(x);
		const glm::vec3 &position = m_particles.getPosition(x);
		std::vector<unsigned int> &neighbors = m_neighborSearch->getNeighbors(x);
		glm::vec3 sum_value(0.0f);
		for (unsigned int y = 0; y < neighbors.size(); ++y)
		{
			unsigned int neighborIndex = neighbors[y];
			if (neighborIndex < nFluidParticles)
			{
				const real density_j = m_density[neighborIndex];
				const glm::vec3 &position_j = m_particles.getPosition(neighborIndex);
				const glm::vec3 &velocity_j = m_particles.getVelocity(neighborIndex);
				glm::vec3 tmp = velocity - velocity_j;
				tmp *= SPHKernels::poly6WKernel(position - position_j) 
					* (m_particles.getMass(neighborIndex) / density_j);
				sum_value -= tmp;
			}
		}
		sum_value *= m_viscosity;
		m_particles.setVelocity(x, velocity + sum_value);
	}
}

10、流体模拟

  最后就是将以上的步骤串联起来，构成模拟一帧流体的全部步骤，代码如下所示，对应了前面PBF的伪代码。

void FluidModelSolver::simulate()
{
	unsigned int nFluidParticles = m_lambda.size();
	const real m_timeStep = m_timeMgr->getTimeStepSize();

	// gravity acceleration.
	clearAccelerations();

	// Update time step size by CFL condition
	updateTimeStepSizeCFL(0.0001, 0.005);

	// predict particles' position and velocity.
	parallel_for(blocked_range<size_t>(0, nFluidParticles, 5000),
		[&](blocked_range<size_t> &r)
	{
		for (size_t x = r.begin(); x != r.end(); ++x)
		{
			m_deltaPos[x] = glm::vec3(0.0);
			m_particles.setLastPosition(x, m_particles.getOldPosition(x));
			m_particles.setOldPosition(x, m_particles.getPosition(x));
			PositionBasedFluids::semiImplicitEuler(
				m_timeStep,
				m_particles.getMass(x),
				m_particles.getPosition(x),
				m_particles.getVelocity(x),
				m_particles.getAcceleration(x));
		}
	});

	// search each particle's neighborhood.
	m_neighborSearch->neighborhoodSearch(m_particles.getPositionGroup(),
		0, nFluidParticles);

	// perform density constraint.
	constraintProjection();

	// update velocities.
	parallel_for(blocked_range<size_t>(0, nFluidParticles, 5000),
		[&](blocked_range<size_t> &r)
	{
		for (size_t x = r.begin(); x != r.end(); ++x)
		{
			PositionBasedFluids::velocityUpdateFirstOrder(
				m_timeStep,
				m_particles.getMass(x),
				m_particles.getPosition(x),
				m_particles.getOldPosition(x),
				m_particles.getVelocity(x)
			);
		}
	});

	// compute viscoity.
	computeXSPHViscosity();
	computeVorticityConfinement();

	// update time stamp.
	m_neighborSearch->updateTimestamp();
	m_timeMgr->setTime(m_timeMgr->getTime() + m_timeStep);
}

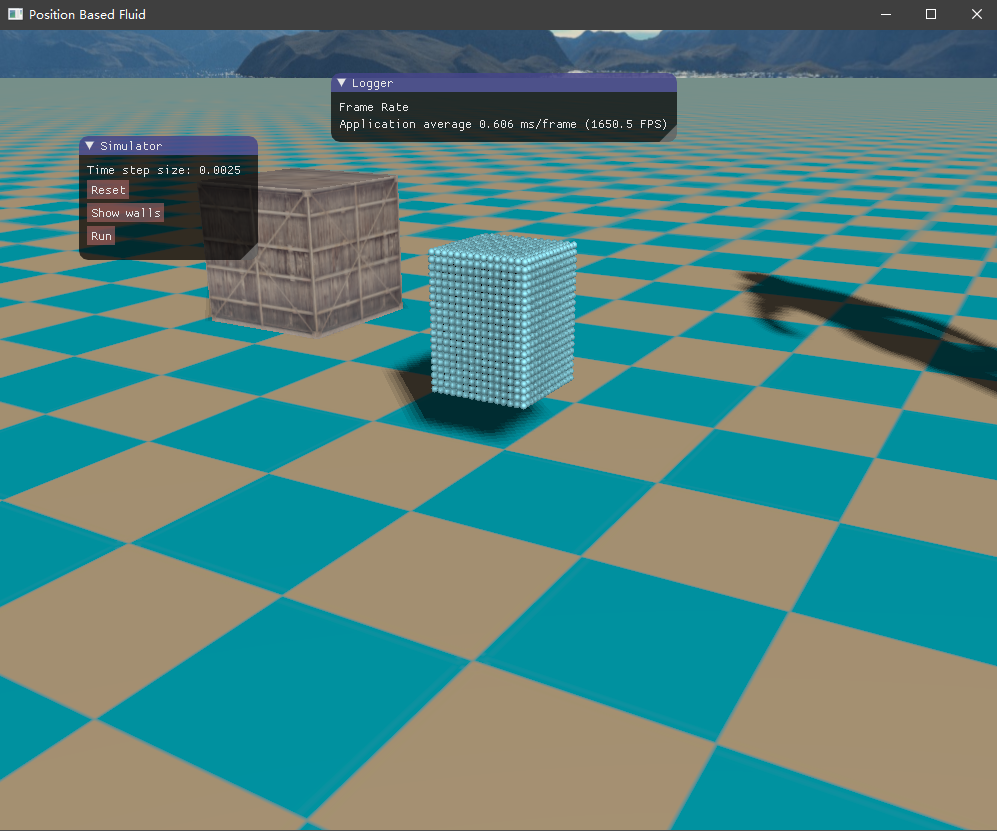
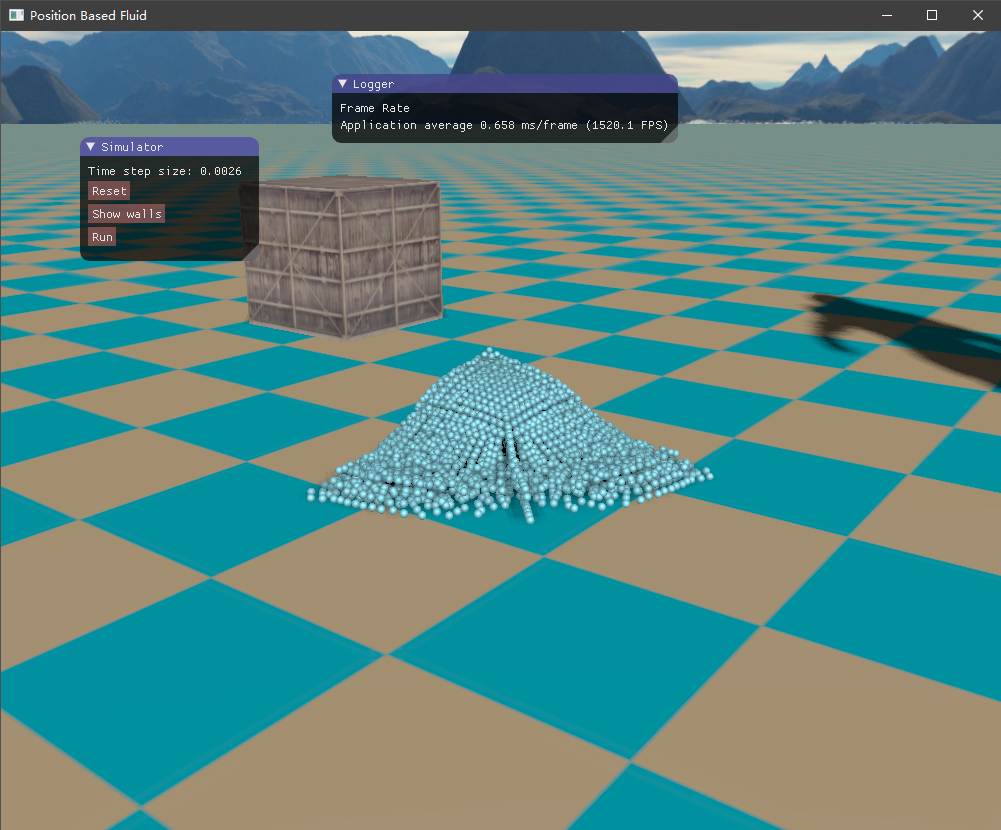
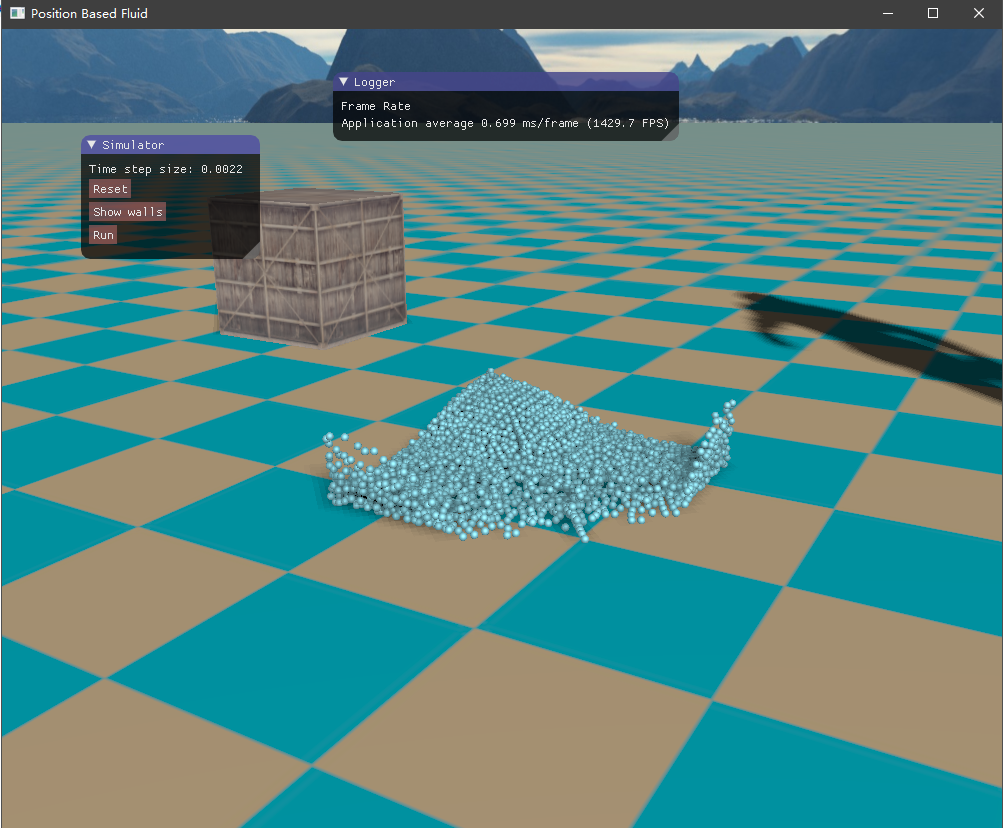
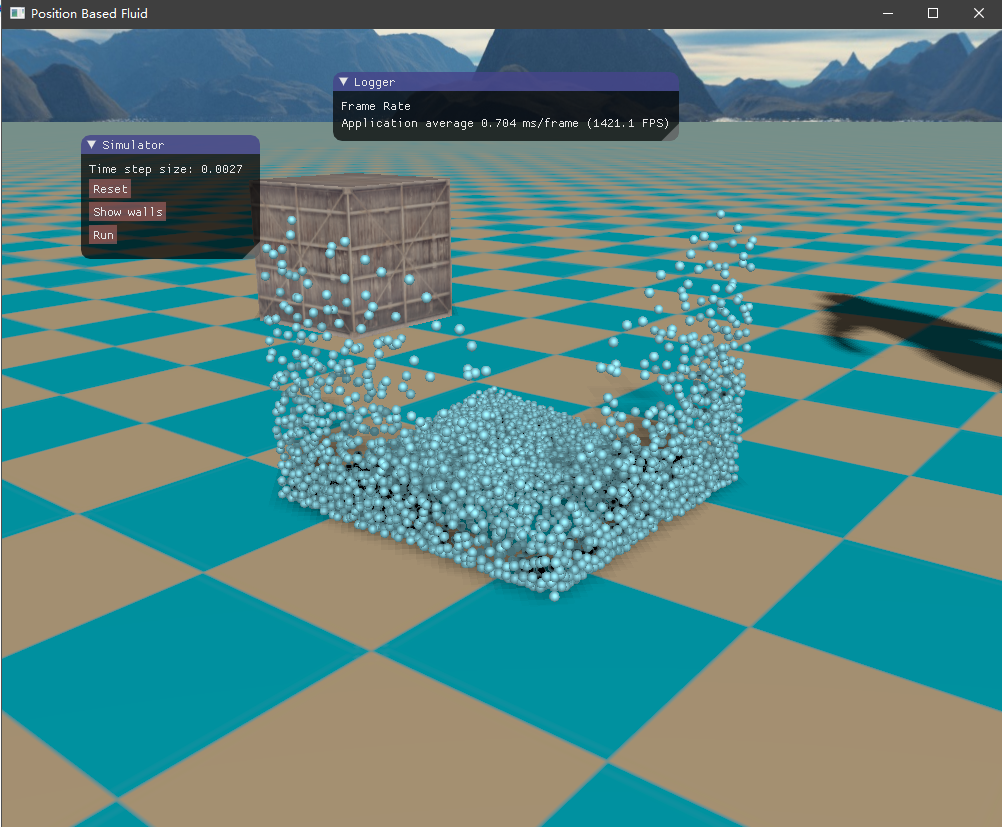
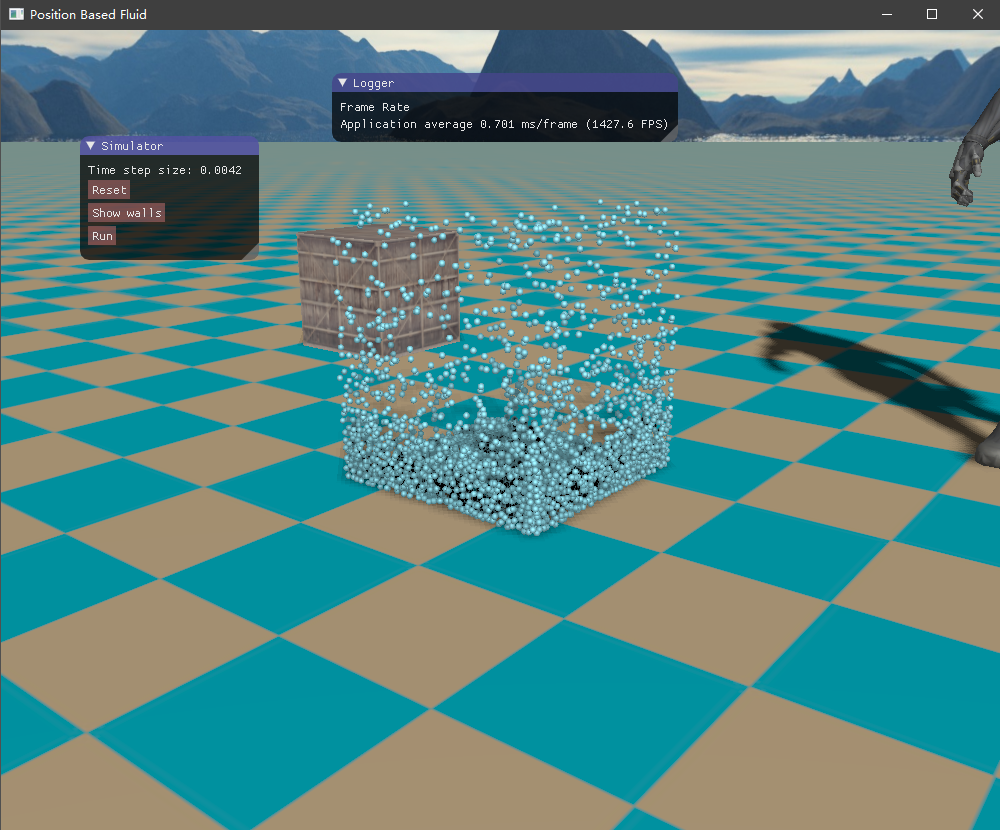
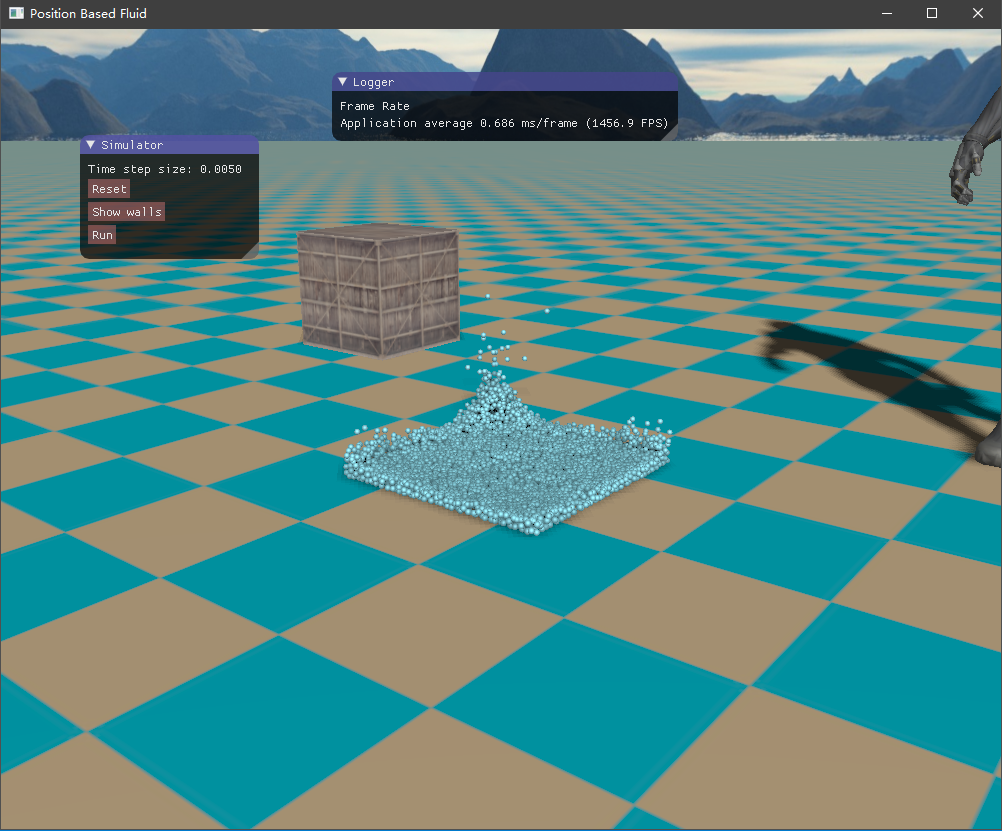
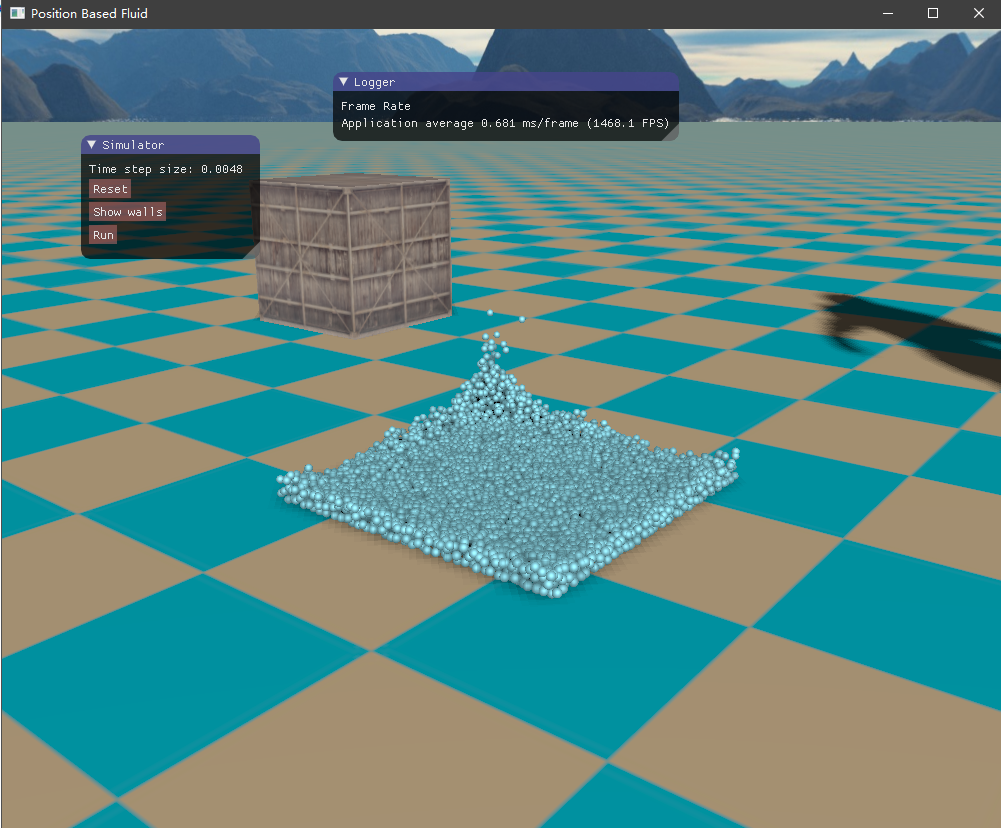
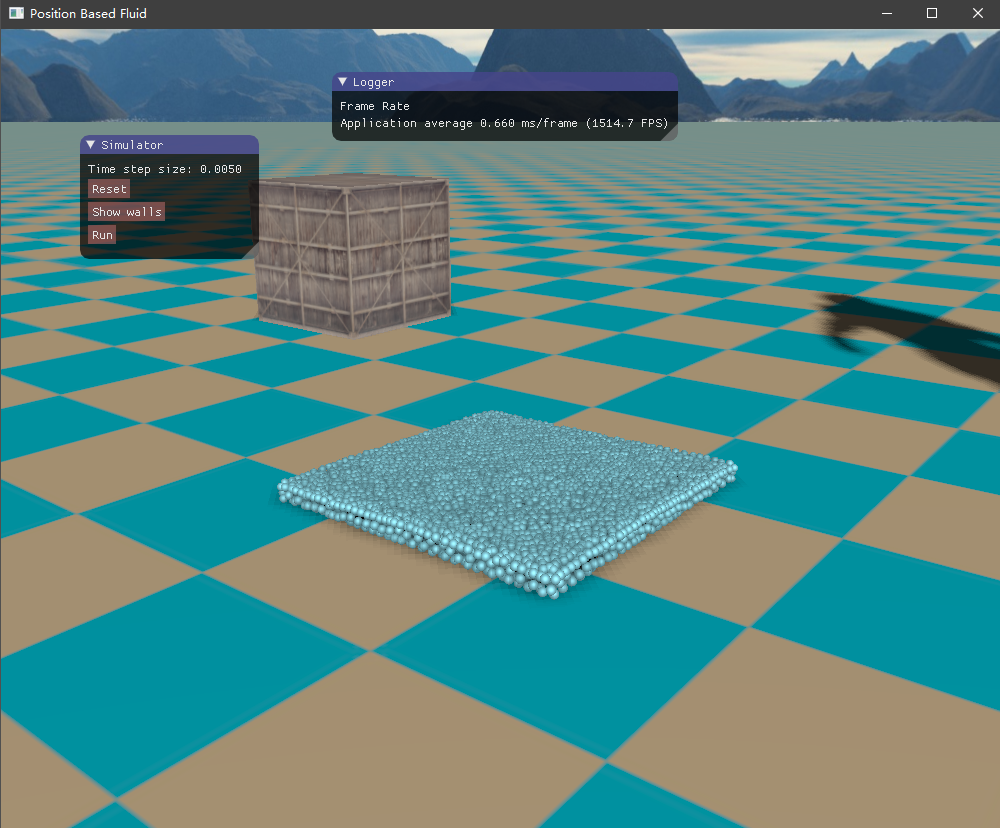
四、实现效果

  目前尚未了解流体渲染，所以只是简单地将流体粒子绘制出来，查看模拟的效果如何。绘制API采用了OpenGL的实例化渲染，UI界面则是接用的ImGui库。测试的场景是一个长方体的流体落下来，碰撞到盒子边界。

  这是初始的流体块，长方体形状

  然后是容器边界，如下所示，它将流体包含在内，也是采用粒子的形式表示。

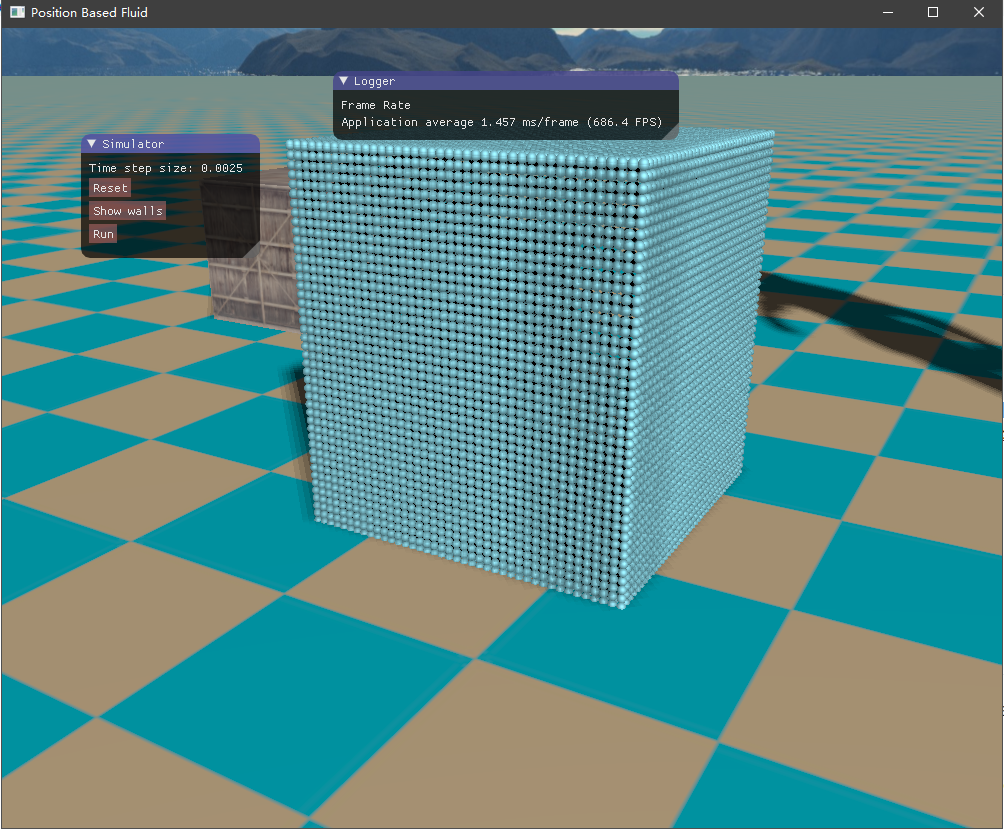
  初始时由于重力加速度的作用，流体将落下来，碰撞到容器边界，然后流体翻滚，最终经过一段时间后趋于平静。

参考资料：

$[1]$ Müller, Matthias, et al. “Position based dynamics.” Journal of Visual Communication and Image Representation 18.2 (2007): 109-118.

$[2]$ Macklin, Miles, and Matthias Müller. “Position based fluids.” ACM Transactions on Graphics (TOG) 32.4 (2013): 104.

$[3]$ M¨ULLER, M., CHARYPAR, D., AND GROSS, M. 2003. Particlebased fluid simulation for interactive applications. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, SCA ’03, 154–159.

$[4]$ Akinci, Nadir, et al. “Versatile rigid-fluid coupling for incompressible SPH.” ACM Transactions on Graphics (TOG) 31.4 (2012): 62.

$[5]$ https://zhuanlan.zhihu.com/p/48737753

$[6]$ https://zhuanlan.zhihu.com/p/49536480