本渲染器已完全重构,与之前版本大不相同,详情移步至TinySoftRenderer 。
一、渲染管线框架 渲染管线的搭建主要包含像素显示、网格数据封装、渲染循环、帧率fps计算、帧缓冲、着色器、渲染逻辑、光栅化等等,其中光栅化作为重点对象抽出来放在后面。当然我们不会一下子就完成渲染管线的基本功能,我们现在是要搭建一个框架,大部分的内容不用写入或者仅仅是做简单的处理,这样后面完善软渲染器的时候只需在相应的位置填写相应的代码逻辑即可。本章目标就是搭建一个渲染管线,用光栅化算法画三角形。当然,如果仅仅是画一个三角形,当然不用这么麻烦,但是我的目标是实现三维的软渲染器,深入理解三维渲染的整个流程,得从基础一步一步慢慢来。
1、像素显示的画布 渲染器最终渲染出来的是一个像素矩阵,我们要把这个像素矩阵显示出来。显示的方法有很多,因人而异,这里我采用自己最熟悉的$Qt$来实现。显示的窗口继承一个普通的$QWidget$父类,然后我们通过重写它的$paintEvent$函数,将渲染出来的像素画到$QWidget$上。但是采用$QPainter$直接画上去的方式效率非常低,我通过查询资料得知,若想要快速地绘制给定的像素矩阵,可以利用$QImage$来实现。话不多说,上代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Window :public QWidget{ Q_OBJECT public : explicit Window (QWidget *parent = nullptr ) ~Window(); private : void paintEvent (QPaintEvent *) override private : Ui::Window *ui; QImage *canvas; };
接收到一帧的像素之后,在重绘事件里面利用$QImage$绘制给定的像素数组(记得调用$update$触发重绘事件)。由于篇幅原因,我不会讲太多细节方面的东西,代码也不会全部放出来,那样没意义。想看完整源代码的朋友直接去本人的github上看。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void Window::receiveFrame(unsigned char *image){ if (canvas) delete canvas; canvas = new QImage(image, width(), height(), QImage::Format_RGBA8888); update(); } void Window::paintEvent(QPaintEvent *event){ if (canvas) { QPainter painter (this ) ; painter.drawImage(0 , 0 , *canvas); } QWidget::paintEvent(event); }
2、帧缓冲类 帧缓冲通常包含基本的颜色缓冲附件、深度缓冲附件等,这里我们暂且只实现颜色缓冲附件(四通道,格式为$RGBA$,各占一个字节),深度缓冲附件后面再加上。渲染管线最终的渲染结果是写入帧缓冲的,我们采用一个一维的单字节数组作为帧缓冲的颜色缓冲。帧缓冲的最基本的功能就是清楚缓冲区、写入像素:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 class FrameBuffer { private : int m_width, m_height, m_channel; std ::vector <unsigned char > m_colorBuffer; public : FrameBuffer(int width, int height); ~FrameBuffer() = default ; int getWidth () return m_width;} int getHeight () return m_height;} unsigned char *getColorBuffer () return m_colorBuffer.data();} void clearColorBuffer (const Vector4D &color) void drawPixel (unsigned int x, unsigned int y, const Vector4D &color) }; FrameBuffer::FrameBuffer(int width, int height) :m_channel(4 ), m_width(width), m_height(height) { m_colorBuffer.resize(m_width*m_height*m_channel, 255 ); } void FrameBuffer::clearColorBuffer(const Vector4D &color){ unsigned char red = static_cast <unsigned char >(255 *color.x); unsigned char green = static_cast <unsigned char >(255 *color.y); unsigned char blue = static_cast <unsigned char >(255 *color.z); unsigned char alpha = static_cast <unsigned char >(255 *color.w); for (int row = 0 ;row < m_height;++ row) { for (int col = 0 ;col < m_width;++ col) { m_colorBuffer[row*m_width*m_channel+col*m_channel + 0 ] = red; m_colorBuffer[row*m_width*m_channel+col*m_channel + 1 ] = green; m_colorBuffer[row*m_width*m_channel+col*m_channel + 2 ] = blue; m_colorBuffer[row*m_width*m_channel+col*m_channel + 3 ] = alpha; } } } void FrameBuffer::drawPixel(unsigned int x, unsigned int y, const Vector4D &color){ if (x < 0 || x >= m_width || y < 0 || y >= m_height) return ; unsigned char red = static_cast <unsigned char >(255 *color.x); unsigned char green = static_cast <unsigned char >(255 *color.y); unsigned char blue = static_cast <unsigned char >(255 *color.z); unsigned char alpha = static_cast <unsigned char >(255 *color.w); unsigned int index = y*m_width*m_channel + x*m_channel; m_colorBuffer[index + 0 ] = red; m_colorBuffer[index + 1 ] = green; m_colorBuffer[index + 2 ] = blue; m_colorBuffer[index + 3 ] = alpha; }
3、网格顶点数据 三维的渲染程序中的顶点数据通常包含顶点位置、顶点颜色、纹理坐标、顶点法线,然后在此基础上利用一组给定顺序的顶点数据表示一个网格,渲染时网格的数据将被送入管线进行处理。为此,有必要对顶点数据做一定的封装。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Vertex { public : Vector4D position; Vector4D color; Vector2D texcoord; Vector3D normal; Vertex() = default ; Vertex(Vector4D _pos, Vector4D _color, Vector2D _tex, Vector3D _normal) :position(_pos),color(_color),texcoord(_tex),normal(_normal) {} Vertex(const Vertex &rhs) :position(rhs.position),color(rhs.color),texcoord(rhs.texcoord),normal(rhs.normal){} };
顶点数据经过顶点着色器的处理之后,会被送到下一个渲染管线的阶段处理。顶点着色器的顶点数据输出与输入有些差异,为此我们也定义一个类表示为顶点着色器的输出,这对于构建渲染管线尤为重要。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class VertexOut { public : Vector4D posTrans; Vector4D posH; Vector2D texcoord; Vector3D normal; Vector4D color; double oneDivZ; VertexOut() = default ; VertexOut(Vector4D _posT, Vector4D _posH, Vector2D _tex, Vector3D _normal, Vector4D _color, double _oneDivZ) :posTrans(_posT),posH(_posH),texcoord(_tex), normal(_normal),color(_color),oneDivZ(_oneDivZ) {} VertexOut(const VertexOut& rhs) :posTrans(rhs.posTrans), posH(rhs.posH), texcoord(rhs.texcoord), normal(rhs.normal), color(rhs.color), oneDivZ(rhs.oneDivZ) {} };
然后就是关于网格的表示,为了节省空间(特别是对于很大的模型),我们直接采用索引来组织网格。若想详细了解OpenGL的顶点索引概念请看这里 。一个网格有两个数组,分别是$Vertex$数组和$Index$数组。下面的代码中,有一个$asTriangle$方法,这是一个三角形网格,调用这个方法之后网格存储的就是一个三角形,用于后面的光栅化调试,光栅化的基本单元就是三角形。通常情况,所有的网格模型都可以用一定数量的三角形构成,因而我们实现的软渲染器的基本图元就是三角形。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 class Mesh { public : std ::vector <Vertex> vertices; std ::vector <unsigned int > indices; Mesh() = default ; ~Mesh() = default ; Mesh(const Mesh& mesh) :vertices(mesh.vertices), indices(mesh.indices){} Mesh& operator =(const Mesh& mesh) { if (&mesh == this ) return *this ; vertices = mesh.vertices; indices = mesh.indices; return *this ; } void setVertices (Vertex* _vs, int count) { vertices.resize(count); new (&vertices[0 ])std ::vector <Vertex>(_vs, _vs + count); } void setIndices (int * _es, int count) { indices.resize(count); new (&indices)std ::vector <unsigned int >(_es, _es + count); } void asBox (double width, double height, double depth) void asTriangle (const Vector3D p1, const Vector3D p2, const Vector3D p3) }; void Mesh::asTriangle(Vector3D p1, Vector3D p2, Vector3D p3){ vertices.resize(3 ); indices.resize(3 ); vertices[0 ].position = p1; vertices[0 ].normal = Vector3D(0.f , 0.f , 1.f ); vertices[0 ].color = Vector4D(1.f , 0.f , 0.f , 1.f ); vertices[0 ].texcoord = Vector2D(0.f , 0.f ); vertices[1 ].position = p2; vertices[1 ].normal = Vector3D(0.f , 0.f , 1.f ); vertices[1 ].color = Vector4D(0.f , 1.f , 0.f , 1.f ); vertices[1 ].texcoord = Vector2D(1.f , 0.f ); vertices[2 ].position = p3; vertices[2 ].normal = Vector3D(0.f , 0.f , 1.f ); vertices[2 ].color = Vector4D(0.f , 0.f , 1.f , 1.f ); vertices[2 ].texcoord = Vector2D(0.5f , 1.f ); indices[0 ] = 0 ; indices[1 ] = 1 ; indices[2 ] = 2 ; }
4、简单的着色器 着色器方面时软渲染中较为高级的内容,目前我们只是搭建一个框架,因而着色器不需要什么复杂的操作,只需简单地传递数据就行了。博主实现的软渲染器只包含必不可少的顶点着色器和片元着色器,目前的顶点着色器将顶点原封不动地输出,片元着色器也是如此,这样我们后面要实现光照效果的时候直接在着色器里写上就行了。为了更加有条理,我们设计一个着色器的虚类,这样实现不同效果的着色器时我们直接继承这个虚类即可。
1 2 3 4 5 6 7 8 9 10 11 12 class BaseShader { public : BaseShader() = default ; virtual ~BaseShader() = default ; virtual VertexOut vertexShader (const Vertex &in) 0 ; virtual Vector4D fragmentShader (const VertexOut &in) 0 ; virtual void setModelMatrix (const Matrix4x4 &world) 0 ; virtual void setViewMatrix (const Matrix4x4 &view) 0 ; virtual void setProjectMatrix (const Matrix4x4 &project) 0 ; };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class SimpleShader :public BaseShader{ public : SimpleShader() = default ; virtual ~SimpleShader() = default ; virtual VertexOut vertexShader (const Vertex &in) virtual Vector4D fragmentShader (const VertexOut &in) virtual void setModelMatrix (const Matrix4x4 &world) virtual void setViewMatrix (const Matrix4x4 &view) virtual void setProjectMatrix (const Matrix4x4 &project) }; VertexOut SimpleShader::vertexShader(const Vertex &in) { VertexOut result; result.posTrans = in.position; result.posH = in.position; result.color = in.color; result.normal = in.normal; result.oneDivZ = 1.0 ; result.texcoord = in.texcoord; return result; } Vector4D SimpleShader::fragmentShader(const VertexOut &in) { Vector4D litColor; litColor = in.color; return litColor; } void SimpleShader::setModelMatrix(const Matrix4x4 &world){ } void SimpleShader::setViewMatrix(const Matrix4x4 &view){ } void SimpleShader::setProjectMatrix(const Matrix4x4 &project){ }
可以看到$SimpleShader$仅仅是将顶点数据直接输出,不进行任何处理。
5、搭建基本的渲染管线 目前我们已经有了一些渲染管线的基本组件,现在就需要把这些组件串起来。首先是渲染循环的问题,$Qt$有它自己的事件循环,而且主线程的事件循环要尽量避免大量的运算(否则UI控件会陷入未响应),因此将渲染循环放到子线程里是一个不错的渲染,这样也可以避免我们的软渲染逻辑与$Qt$的接口耦合得太高。
渲染线程 $Qt$提供了$QThread$类构建线程,我采用的方式为:渲染循环类继承$QObject$,然后调用$moveToThread$番方法挂到子线程上运行,最后将线程的启动信号与$loop$渲染循环关联即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 class RenderLoop :public QObject{ Q_OBJECT public : explicit RenderLoop (int w, int h, QObject *parent = nullptr ) ~RenderLoop(); void stopIt () true ;} void setFpsZero () 0 ;} int getFps () return fps;} signals: void frameOut (unsigned char *image) public slots: void loop () private : bool stoped; int fps; int width, height, channel; }; RenderLoop::RenderLoop(int w, int h, QObject *parent) : QObject(parent), width(w), height(h), channel(4 ) { fps = 0 ; stoped = false ; } RenderLoop::~RenderLoop() { } void RenderLoop::loop(){ ...... fps = 0 ; while (!stoped) { ...... ++ fps; } }
然后在主窗口中创建$RenderLoop$对象,挂到$QThread$上启动。此外还有一点要注意的是在子线程中最好不用使用$QTimer$类,因此我在主窗口中创建$QTimer$类,设定为每秒触发,触发时主线程读取子线程的$fps$,这样就达到了显示帧率的目的了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 在Window类声明处: private : QTimer *timer; QThread *loopThread; RenderLoop *loop; 在Window类构造函数处: loop = new RenderLoop(width(), height(), nullptr ); loopThread = new QThread(this ); timer = new QTimer(); connect(timer,&QTimer::timeout,this ,&Window::fpsTimeOut); loop->moveToThread(loopThread); connect(loopThread,&QThread::finished,loop, &RenderLoop::deleteLater); connect(loopThread,&QThread::started,loop,&RenderLoop::loop); connect(loop,&RenderLoop::frameOut,this ,&Window::receiveFrame); loopThread->start(); timer->start(1000 ); Window的其他函数: void Window::fpsTimeOut(){ int fps = loop->getFps(); loop->setFpsZero(); this ->setWindowTitle(QString(" fps: %1" ).arg(fps)); }
渲染流程 回顾一下$OpenGL$的渲染流程(这里只考虑一般的情况,即不包含几何着色器、细分着色器等),首先外部处理网格,将网格顶点数据和网格顶点索引送入渲染管线,设置基本图元(如三角形)、渲染方式(如线框模式)。渲染管线的第一阶段为顶点着色器阶段(在这之前还有个缓冲清理阶段),顶点着色器对网格数据逐顶点处理(包含坐标空间变换、投影变换等等),随之输出。然后渲染管线对输出的顶点数据进行裁剪,送入光栅化部件,计算几何图元覆盖的像素点,其中进行了大量的线性插值操作。接着片元着色器获取光栅化后的像素,对每个像素做颜色计算等,然后输出颜色数据、深度数据,最后根据这些缓冲数据做深度测试。
所以一个最基本的渲染管线应该有如下几个步骤:
初始化(如缓冲区创建)$\to$输入顶点缓冲、索引缓冲$\to$清除缓冲区$\to$设置着色器、渲染方式$\to$绘制$\to$交换双缓冲$\to$输出。根据这些步骤,创建$Pipeline$类如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 class Pipeline { private : int m_width, m_height; BaseShader *m_shader; FrameBuffer *m_frontBuffer; FrameBuffer *m_backBuffer; Matrix4x4 viewPortMatrix; std ::vector <Vertex> m_vertices; std ::vector <unsigned int > m_indices; public : Pipeline(int width, int height); ~Pipeline(); void initialize () void clearBuffer (const Vector4D &color, bool depth = false ) void setVertexBuffer (const std ::vector <Vertex> &vertices) void setIndexBuffer (const std ::vector <unsigned int > &indices) void setShaderMode (ShadingMode mode) void drawIndex (RenderMode mode) void swapBuffer () unsigned char *output () return m_frontBuffer->getColorBuffer();} }; Pipeline::Pipeline(int width, int height) :m_width(width),m_height(height) ,m_shader(nullptr ),m_frontBuffer(nullptr ) ,m_backBuffer(nullptr ) { } Pipeline::~Pipeline() { if (m_shader)delete m_shader; if (m_frontBuffer)delete m_frontBuffer; if (m_backBuffer)delete m_backBuffer; m_shader = nullptr ; m_frontBuffer = nullptr ; m_backBuffer = nullptr ; } void Pipeline::initialize(){ if (m_frontBuffer) delete m_frontBuffer; if (m_backBuffer) delete m_backBuffer; if (m_shader) delete m_shader; viewPortMatrix.setViewPort(0 ,0 ,m_width,m_height); m_frontBuffer = new FrameBuffer(m_width, m_height); m_backBuffer = new FrameBuffer(m_width, m_height); m_shader = new SimpleShader(); } void Pipeline::drawIndex(RenderMode mode){ 输入顶点着色器; 光栅化; 输入片元着色器; 写入缓冲区; } void Pipeline::clearBuffer(const Vector4D &color, bool depth){ (void )depth; m_backBuffer->clearColorBuffer(color); } void Pipeline::setShaderMode(ShadingMode mode){ if (m_shader)delete m_shader; if (mode == ShadingMode::simple) m_shader = new SimpleShader(); else if (mode == ShadingMode::phong) ; } void Pipeline::swapBuffer(){ FrameBuffer *tmp = m_frontBuffer; m_frontBuffer = m_backBuffer; m_backBuffer = tmp; }
注意到我创建了帧缓冲,分别是$m_frontBuffer$和$m_backBuffer$,前者存储着当前显示的像素,后者缓冲区用于写入像素。这就是著名的双缓冲原理,可以避免画面的闪烁、撕裂等现象。除此之外,还有一个值得特别说明的就是视口变换矩阵$viewPortMatrix$,这个一般很少见到,因为被内嵌在了渲染管线里面了。经过投影变换、透视除法操作之后,顶点数据都在标准化设备空间中,即$x$轴、$y$轴、$z$轴取值范围为$[-1,1]$。但是屏幕的像素坐标范围并非如此,通常屏幕的$x$轴坐标范围为$[0,width]$,$y$轴坐标范围为$[0,height]$,屏幕像素坐标原点在左上角,$x$轴正向朝右,$y$轴正向朝下,所以我们还要把标准化设备坐标顶点数据变换到屏幕的坐标范围中,这就是视口变换 ($z$轴一般保持不变)。视口变换矩阵的构造并没有难度,因为这仅仅是简单的线性映射,因此不再赘述。视口变换矩阵如下所示:
其中$(s_x,s_y)$是视口左上角的坐标,$(w,h)$为屏幕的宽度和高度。
1 2 3 4 5 6 7 8 void Matrix4x4::setViewPort(int left, int top, int width, int height){ loadIdentity(); entries[0 ] = static_cast <float >(width)/2.0f ; entries[5 ] = -static_cast <float >(height)/2.0f ; entries[12 ] = static_cast <float >(left)+static_cast <float >(width)/2.0f ; entries[13 ] = static_cast <float >(top)+static_cast <float >(height)/2.0f ; }
$Pipeline$还有个非常重要的函数$drawIndex$,它是渲染管线的核心部分,涉及到了图元装配、顶点着色器调度、光栅化、片元着色器调度、写入帧缓冲这几个重要的步骤。我们实现的软渲染器几何图元默认为三角形,所以图元装配就是每三个顶点装成一个图元。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 void Pipeline::drawIndex(RenderMode mode){ if (m_indices.empty())return ; for (unsigned int i = 0 ;i < m_indices.size()/3 ;++ i) { Vertex p1,p2,p3; { p1 = m_vertices[3 *i+0 ]; p2 = m_vertices[3 *i+1 ]; p3 = m_vertices[3 *i+2 ]; } VertexOut v1,v2,v3; { v1 = m_shader->vertexShader(p1); v2 = m_shader->vertexShader(p2); v3 = m_shader->vertexShader(p3); } { v1.posH = viewPortMatrix * v1.posH; v2.posH = viewPortMatrix * v2.posH; v3.posH = viewPortMatrix * v3.posH; if (mode == RenderMode::wire) { } else if (mode == RenderMode::fill) { } } } }
有了以上的$Pipeline$函数,我们的渲染循环逻辑的一般形式如下:
1 2 3 4 5 6 7 8 9 10 11 while (!stoped){ pipeline->clearBuffer(Vector4D(0.502f ,0.698f ,0.800f ,1.0f )); pipeline->drawIndex(RenderMode::fill); pipeline->swapBuffer(); emit frameOut (pipeline->output()) ; ++ fps; }
二、光栅化算法 顶点着色器处理的还是一个个离散的几何顶点,在顶点着色器之后我们还需要进行光栅化操作,将几何覆盖的屏幕像素计算出来,送入片元着色器计算每个点的像素数据。光栅化一般有两种模式:一种是线框模式,即只描绘几何的边;二是填充模式,即将几何的面片全部填充完。Bresenham算法是经典的描线算法,它采用迭代的形式将所需的算术操作降低到最少。除此之外还有DDA描线算法,效率上不如Bresenham算法,所以我没有实现。
1、Bresenham描线算法 我们要描绘的是从$(x_0,y_0)$到$(x_1,y_1)$的一条直线线段。一些数学符号标记如下:
其中$m$即直线线段的斜率,为了便于讨论,我们假设$|m|\leq 1$,其他情况很容易推广。
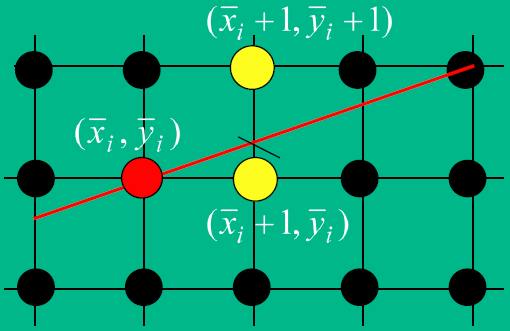
在如上的情况下,Bresenham算法从$x=x_0$开始,每次将$x$坐标值加一,然后推算相应的$y$坐标值。记第$i$次迭代获得的点为$(x_i,y_i)$。那么第$i+1$次迭代时获取的点就在$(\overline x_i+1,\overline y_i)$和$(\overline x_i+1,\overline y_i+1)$这两个中选取。那如何判断应该选哪个呢?即选择这两个点之一的判断标准是什么?直观上,我们应该选取距离的直线线段在该$y$轴上的交点最近的点 ,如下图1所示。
图1 判别标准 直线的一般表达式为$y=mx+B$,$m$为直线的斜率,那么$(x_{i+1},y_{i+1})$表示为如下(注意$y_{i+1}$表示的是直线在$x_{i+1}$上真正的$y$值):
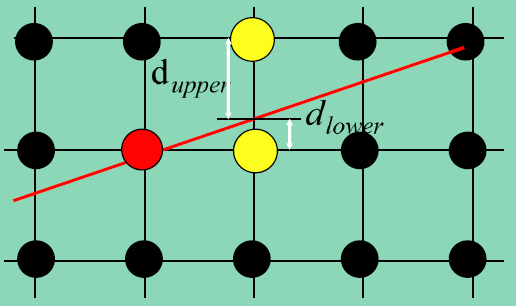
图2 交点到右边的点、右上的点的距离 故$d_{upper}$和$d_{lower}$的取值如下:
显然,如果$d_{lower}-d_{upper}>0$,则应该取右上方的点;如果$d_{lower}-d_{upper}<0$,则应该取右边的点。而$d_{lower}-d_{upper}=0$可任取这两个点。因此,我们的判断标准就是$d_{lower}-d_{upper}>0$的符号。
式$(4)$中的$m$是直线的斜率,因此将式$(4)$作为判断标准需要做非常昂贵的浮点数除法运算。为了消去除法,注意到$m=\frac{\Delta y}{\Delta x}$,两边同时乘上$\Delta x>0$,正负符号不变。
所以可以用$p_i$的符号作为选取的标准。但是,式$(5)$的计算能够进一步简化,考虑$p_i$和$p_{i+1}$(注意我们根据$p_i$的符号来选取$\overline y_{i+1}$):
若$p_i\leq 0$,那么选择右边的点,此时$\overline y_{i+1}=\overline y_i$,那么有:
若$p_i>0$,那么选择右上角的点,此时$\overline y_{i+1}=\overline y_i+1$,那么有:
所以我们可以根据$p_i$的符号快速计算出$p_{i+1}$的符号,如此迭代下去:
Bresenham Algorithm:
$draw (x_0, y_0);$
Calculate $\Delta x$,$\Delta y$,$2\Delta y$,$2\Delta y-2\Delta x$,$p_0=2\Delta y-\Delta x$;
for $x$ from $x_0$ to $x_1$:
if $p_i\leq 0$
draw $(x_{i+1},\overline y_{i+1})=(x_i+1,\overline y_i)$ ;
compute $p_{i+1}=p_i+2\Delta y$;
if $p_i > 0$
draw $(x_{i+1},\overline y_{i+1})=(x_i+1,\overline y_i+1)$ ;
compute $p_{i+1}=p_i+2\Delta y-2\Delta x$;
$x += 1;$
上面我们讨论的都是$|m|<1$的情况,那$|m|>1$的情况呢?其实这是对称的,这时把$x$看成$y$,把$y$看成$x$即可。另外,当$\Delta x <0$时,我们的$x$不是递增$1$,而是递减$1$,具体实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 void Pipeline::bresenhamLineRasterization(const VertexOut &from, const VertexOut &to){ int dx = to.posH.x - from.posH.x; int dy = to.posH.y - from.posH.y; int stepX = 1 , stepY = 1 ; if (dx < 0 ) { stepX = -1 ; dx = -dx; } if (dy < 0 ) { stepY = -1 ; dy = -dy; } int d2x = 2 *dx, d2y = 2 *dy; int d2y_minus_d2x = d2y - d2x; int sx = from.posH.x; int sy = from.posH.y; VertexOut tmp; if (dy <= dx) { int flag = d2y - dx; for (int i = 0 ;i <= dx;++ i) { tmp = lerp(from, to, static_cast <double >(i)/dx); m_backBuffer->drawPixel(sx,sy,m_shader->fragmentShader(tmp)); sx += stepX; if (flag <= 0 ) flag += d2y; else { sy += stepY; flag += d2y_minus_d2x; } } } else { int flag = d2x - dy; for (int i = 0 ;i <= dy;++ i) { tmp = lerp(from, to, static_cast <double >(i)/dy); m_backBuffer->drawPixel(sx,sy,m_shader->fragmentShader(tmp)); sy += stepY; if (flag <= 0 ) flag += d2x; else { sx += stepX; flag -= d2y_minus_d2x; } } } }
2、Edge-Walking三角形填充算法 三角形光栅化填充对输入给定的三个三角形顶点,计算这个三角区域覆盖的所有像素。三角形填充的光栅化算法有很多种,这里仅实现了Edge-Walking算法,此外还有Edge-Equation算法。关于Edge-Walking算法的前世今生我不再赘述了,这个算法的思路比较简单,但是实现起来比较麻烦一点。
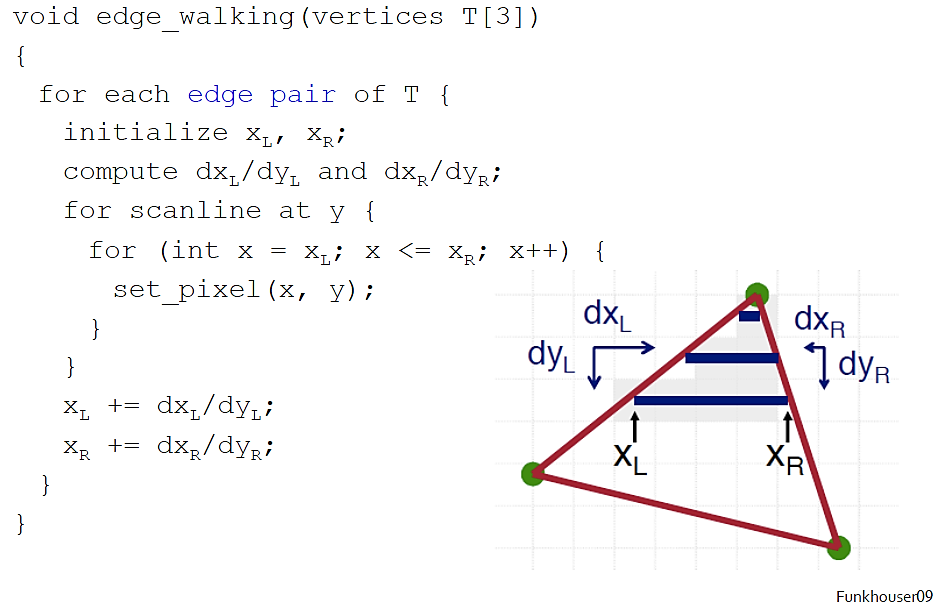
话不多少,直接上伪代码(懒得自己写了伪代码了):
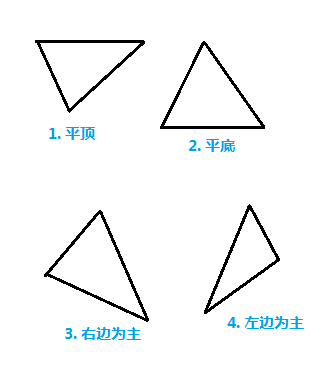
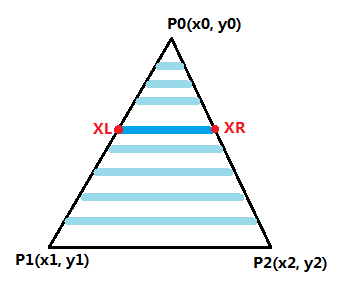
大致的思想就是从上往下(或从下往上)扫描,获取每对$X_L$、$X_R$,然后在$[X_L,X_R]$范围内从左到右扫描。显然就是双重循环。一般,我们的三角形光栅化对象有如下四种情况:
图3 四类三角形 先来看平底三角形的情况,如下图4所示。显然,平底三角形很容易地实现从下往上扫面,竖直方向上仅需考虑左右两条边。
当然这里有个问题,就是如何确定$X_L$和$X_R$?如果直接采用算法伪代码中的利用$dx/dy$迭代获取$X$值,因为$X$值是整数,而$dx/dy$是浮点数,当$dx/dy<1$时,把$dx/dy$加到$X$上面计算机对整数类型坐标自动向下取整,结果相当于没加。(即便是浮点数类型,最终也要取整,因为屏幕空间的像素坐标必须是整数)
图4 平底三角形 一种解决方案就是线性插值,算法从下往上扫描时,$y-=1$,我们根据当前的$y$值来获取$x$值:
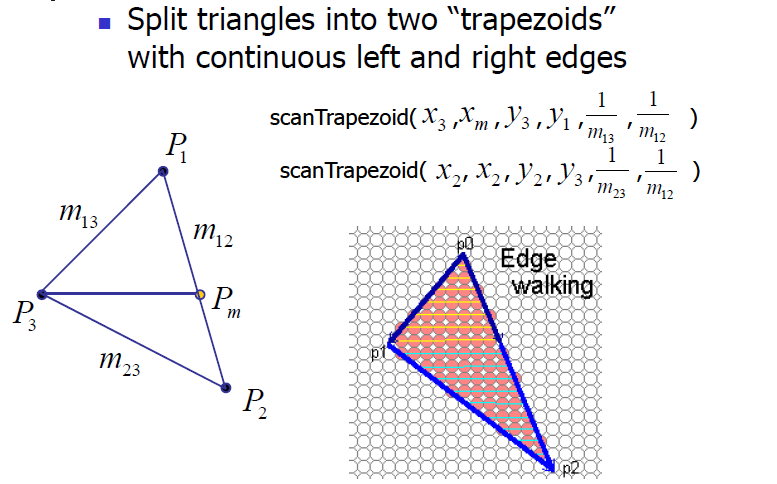
平顶的三角形光栅化亦类似,不再赘述。那么除了平底和平顶的情况之外,我们该如何处理其余的情况?一个技巧就是将其他情况的三角形分割乘一个平底三角形、一个平顶三角形,如下图所示:
图5 三角形分割 这样我们通过调用平底三角形光栅化方法、平顶三角形光栅化方法即可实现一般情况的三角形光栅化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 void Pipeline::scanLinePerRow(const VertexOut &left, const VertexOut &right){ VertexOut current; int length = right.posH.x - left.posH.x + 1 ; for (int i = 0 ;i <= length;++i) { double weight = static_cast <double >(i)/length; current = lerp(left, right, weight); current.posH.x = left.posH.x + i; current.posH.y = left.posH.y; m_backBuffer->drawPixel(current.posH.x, current.posH.y, m_shader->fragmentShader(current)); } } void Pipeline::rasterTopTriangle(VertexOut &v1, VertexOut &v2, VertexOut &v3){ VertexOut left = v2; VertexOut right = v3; VertexOut dest = v1; VertexOut tmp, newleft, newright; if (left.posH.x > right.posH.x) { tmp = left; left = right; right = tmp; } int dy = left.posH.y - dest.posH.y + 1 ; for (int i = 0 ;i < dy;++i) { double weight = 0 ; if (dy != 0 ) weight = static_cast <double >(i)/dy; newleft = lerp(left, dest, weight); newright = lerp(right, dest, weight); newleft.posH.y = newright.posH.y = left.posH.y - i; scanLinePerRow(newleft, newright); } } void Pipeline::rasterBottomTriangle(VertexOut &v1, VertexOut &v2, VertexOut &v3){ VertexOut left = v1; VertexOut right = v2; VertexOut dest = v3; VertexOut tmp, newleft, newright; if (left.posH.x > right.posH.x) { tmp = left; left = right; right = tmp; } int dy = dest.posH.y - left.posH.y + 1 ; for (int i = 0 ;i < dy;++i) { double weight = 0 ; if (dy != 0 ) weight = static_cast <double >(i)/dy; newleft = lerp(left, dest, weight); newright = lerp(right, dest, weight); newleft.posH.y = newright.posH.y = left.posH.y + i; scanLinePerRow(newleft, newright); } } void Pipeline::edgeWalkingFillRasterization(const VertexOut &v1, const VertexOut &v2, const VertexOut &v3){ VertexOut tmp; VertexOut target[3 ] = {v1, v2,v3}; if (target[0 ].posH.y > target[1 ].posH.y) { tmp = target[0 ]; target[0 ] = target[1 ]; target[1 ] = tmp; } if (target[0 ].posH.y > target[2 ].posH.y) { tmp = target[0 ]; target[0 ] = target[2 ]; target[2 ] = tmp; } if (target[1 ].posH.y > target[2 ].posH.y) { tmp = target[1 ]; target[1 ] = target[2 ]; target[2 ] = tmp; } if (equal(target[0 ].posH.y,target[1 ].posH.y)) { rasterBottomTriangle(target[0 ],target[1 ],target[2 ]); } else if (equal(target[1 ].posH.y,target[2 ].posH.y)) { rasterTopTriangle(target[0 ], target[1 ], target[2 ]); } else { double weight = static_cast <double >(target[1 ].posH.y-target[0 ].posH.y)/(target[2 ].posH.y-target[0 ].posH.y); VertexOut newPoint = lerp(target[0 ],target[2 ],weight); newPoint.posH.y = target[1 ].posH.y; rasterTopTriangle(target[0 ], newPoint, target[1 ]); rasterBottomTriangle(newPoint,target[1 ],target[2 ]); } }
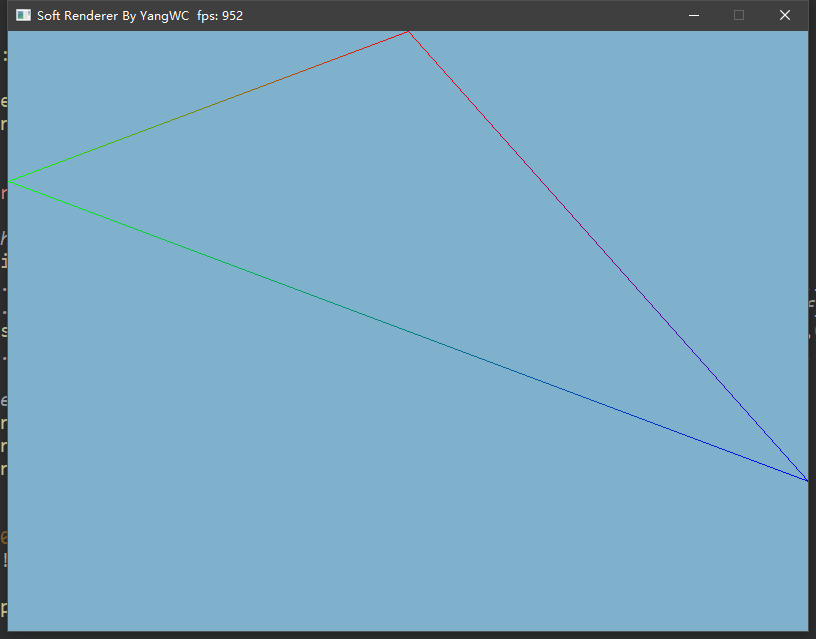
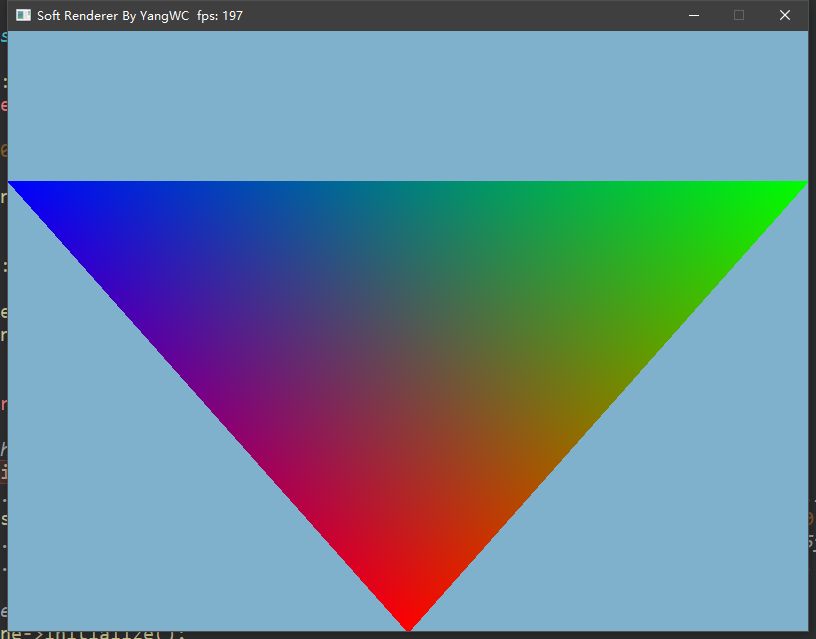
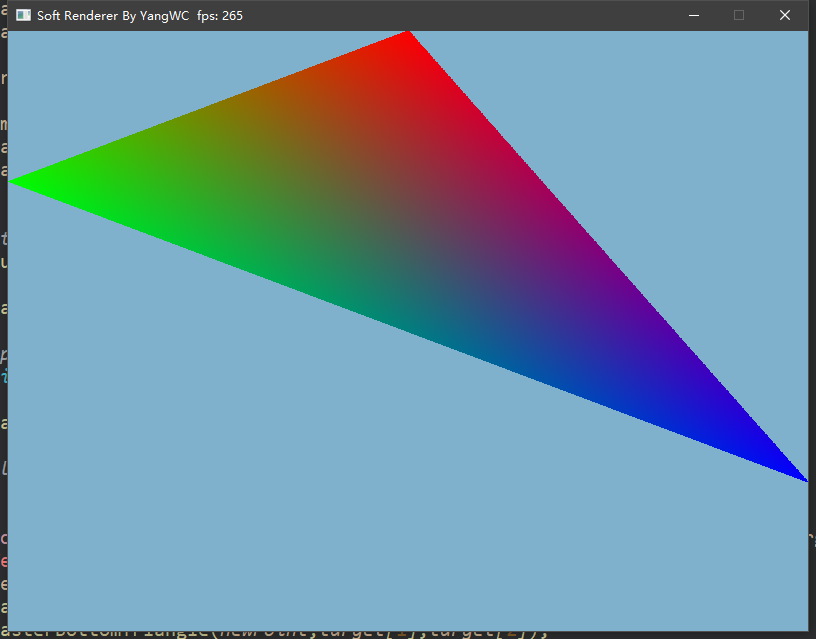
三、程序结果 最终,不借用任何图形接口通过自己实现的光栅化算法画出了三角形:
参考资料 $[1]$ https://blog.csdn.net/cppyin/article/details/6232453
$[2]$ https://blog.csdn.net/y1196645376/article/details/78937614
$[3]$ https://blog.csdn.net/y1196645376/article/details/78907914