高质量实时渲染：实时软阴影

本文是闫令琪老师GAMES202高质量实时渲染课程的学习笔记和总结，这一节的主题为高质量实时阴影。

一、阴影贴图

  阴影贴图技术由来已久，它是一种基于图像空间的方法，因其简单、高效等因素被广泛应用于当今的实时渲染引用中，甚至早期的离线渲染都曾用该技术来生成阴影。阴影贴图概括起来：

• 是一种两个pass的算法，先从光照的视角渲染成并生成深度图，然后再从观察视角渲染并用深度图计算阴影；
• 是一种图像空间的方法，因而无需关注场景中的具体几何形状，但也带来了一些局限性（例如走样）；

图1 Shadow Map的两个pass

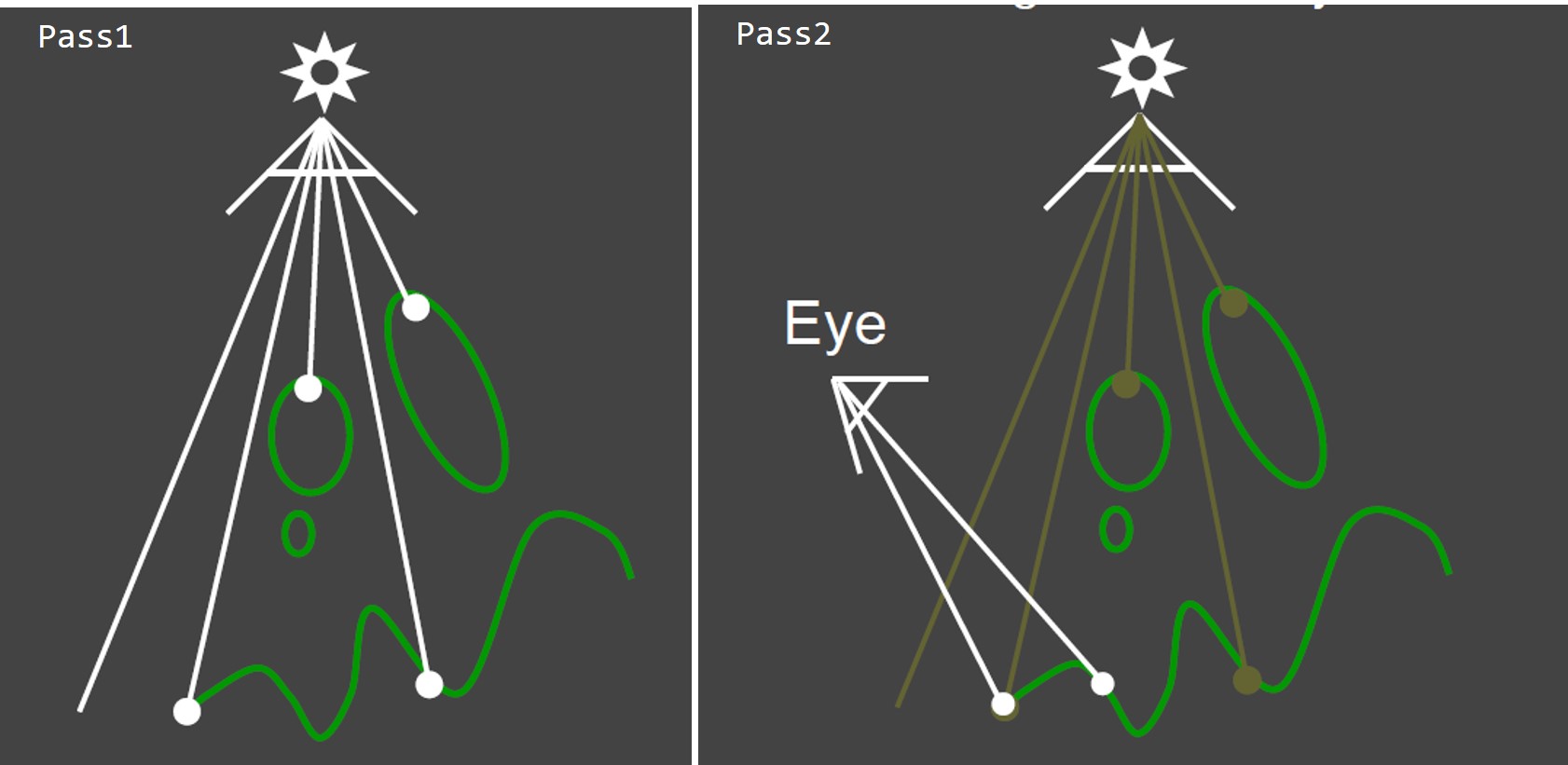
  阴影贴图的原理如图1所示，比较简单，这里不再赘述。简单粗暴的阴影贴图有很大局限性，主要体现在：

• 由于深度图的有限分辨率带来的自遮挡阴影失真，在光与阴影接收面法线夹角很大的时候非常明显；

• 由于深度图的有限分辨率带来的阴影轮廓走样锯齿问题；

• 阴影太过生硬，阴影区域到非阴影区域无平滑柔和的过度，即只能产生硬阴影。

  自遮挡问题的产生原因见如图2所示，其中黄色线代表深度图存储的最近深度。受限于分辨率，在距离光源比较远的情况下，多个片段可能从深度贴图的同一个值中去采样，因此存在一定的深度偏差，在某些地方读取的阴影贴图深度偏大，有些地方偏小，最终导致产生隔间性的阴影条带，如图3所示。

图2 自遮挡问题产生原因

图3 自遮挡问题导致的条带状

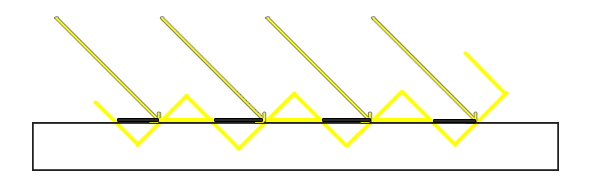
  这种失真现象在光与接收平面法线夹角增大时更加明显（注：此失真现象并非为摩尔纹）。一种解决方案就是使用阴影偏移，对深度图采样得到的深度值减去一个$\epsilon$，本质上就是把最近的深度往光的方向再移动了一下。但阴影偏移的技巧容易产生阴影悬浮，即稍微阴影偏离了本来的位置，使得产生阴影的物体看起来像是漂浮起来了。为了解决悬浮问题，可以在第一个pass的时候设置前向面剔除。

  另一种解决自遮挡问题的方法则是用深度图存储次小深度。如下图4所示，这种方法实现起来也简单，但需要两个pass来生成阴影贴图，第一个pass绘制时设置为背向面剔除，第二个pass绘制时设置为前向面剔除，这样就可以得到介于两者之间的深度值，用以计算阴影。

图4 次小深度阴影贴图生成

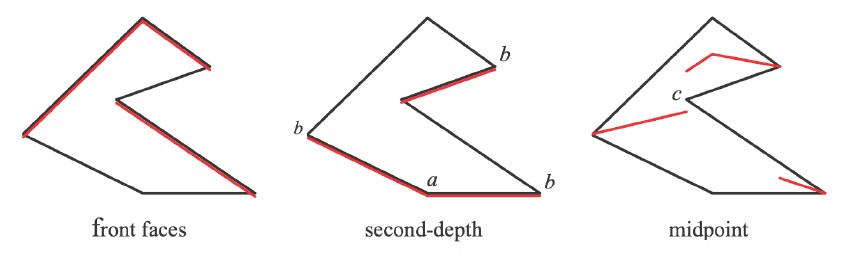
  但这种方法要求投射阴影的物体必须为闭合曲面（watertight），而且再多一个pass必然带来更大的开销，因此并没有得到广泛的应用（实时渲染不相信算法渐进复杂度）。阴影贴图的另外两个问题（锯齿和硬阴影）的解决，将在后面叙述。

二、阴影贴图的数学原理

  实时渲染领域并不关注严谨、严格的数学证明，只关注是否能够work。一个常用的积分近似公式如下所示：

$$\int_{\Omega} f(x)g(x)dx\approx \frac{\int_{\Omega}f(x)dx}{\int_{\Omega}dx}\cdot \int_{\Omega}g(x)dx \tag {1}$$

  当满足以下任一条件时，公式$(1)$的近似能够得到一个相对准确的结果：

• 当$g(x)$在积分域$\Omega$内的实际贡献很小，即$g(x)$在$\Omega$内绝大部分取值为零，例如一个脉冲函数，仅在$x=0$不为零，其他地方均为零（即狄拉克函数）；

• 当$g(x)$在积分域$\Omega$内变化不大，即最大值和最小值差别很小（甚至相同，即常量函数）。

  回到Shadow mapping原理上，其本质上就是把渲染方程中的可见性函数提取出来单独进行积分，从而得到近似的积分结果：

$$\begin{align} L_o(p,\omega_o) =&\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)cos\theta_i V(p,\omega_i)d\omega_i\\ \approx&\frac{f_{\Omega^+}V(p,\omega_i)d\omega_i}{\int_{\Omega^+}d\omega_i} \cdot \int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)cos\theta_i d\omega_i \end{align} \tag {2}$$

  这种近似在实时应用领域应用广泛，通常的应用场景下，$L_i$来自于点光源或者平行光源，因而满足上面提到的条件一，或者$f_r$函数取值变化不大（例如漫反射brdf），符合上面提到的条件二。阴影贴图做的事就是把公式$(2)$的可见性函数先计算出来，然后再与光照项进行相乘，得到最终的渲染结果。

三、PCSS软阴影算法

  前面提到，阴影贴图的一个缺点就是受限于贴图的分辨率大小容易产生明显的走样现象，根本原因还是采样频率没有跟上。暴力增加分辨率进行超采样的方法这里不再赘述。常用的解决方法就是对采样得到可见性信号进行滤波，这就是PCF（Percentage Close Filtering）。在计算可见性时，PCF不再仅仅只查单独的一个深度值，而是会将着色器点$p$的深度值与深度贴图上的周围最近深度进行比较，最终对比较的结果进行一个加权平均，得到最终的结果。这样本质上就是对可见性信号进行了滤波（注意：并非是对深度图进行了滤波）。经过PCF滤波的阴影在边缘部分能够得到明显的缓和，如图5所示。

图5 有无PCF的阴影比较

  PCF的滤波半径决定了阴影边缘的柔和程度，一般来说滤波半径越大则柔和，相反阴影边缘越锐利，如图6所示。由此启发了PCSS（Percentage Close Soft Shadow）软阴影算法的核心原理，对于那些我们需要实现软阴影的边缘用更大的滤波半径进行滤波，而对于那些不需要太过柔和阴影边缘的地方，则采用更小的滤波半径，这是一种自适应滤波半径的机制。

图6 不同PCF滤波半径得到的阴影

  PCSS的本质，概括起来就是自适应PCF滤波半径的阴影贴图算法。其关键核心在于如何制定自适应滤波半径的机制。仔细观察图7，可以看到阴影区域在越靠近遮挡物的地方越硬，而越原理遮挡物的地方则越软，因此我们希望根据投影区域到遮挡物的距离来调整PCF滤波半径的大小。

图7 阴影柔和程度的变化

  在此之前，先明确一个概念，点光源作为理想中的光源类型，不存在软阴影，而现实世界的光都具有一定的面积。阴影的软化程度本质上取决于半影区域的大小，半影区域越大则阴影越柔和，因此我们首先推算给定光源、给定遮挡物下和给定投影区域上的半影大小（即如下图8所示的$W_{Penumbra}$）。

图8 半影长度推算

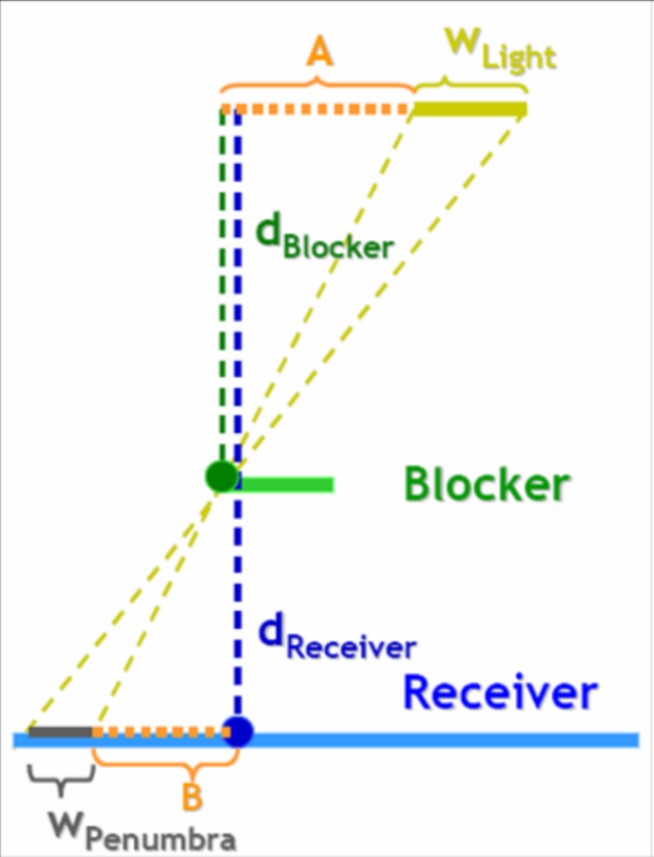
  由三角形相似可以得到：

$$W_{Penumbra}=(d_{Receiver}-d_{Blocker})\cdot w_{light}/d_{Blocker} \tag {3}$$

  其中，$d_{Receiver}$是阴影接收区域到光源的距离，$d_{Blocker}$是遮挡物到光源的距离，这两个参数都可以直接从第一个pass生成的深度图获取得到，光源面积$w_{light}$由我们自己手动指定。公式$(3)$计算得到的半影长度就可以作为PCF滤波半径的大小参数。因此，完整的PCSS算法如下所示：

图9 PCSS算法步骤

  其中第一步用于计算$d_{Blocker}$，方式与PCF类似，对周围深度信息进行采样，如果判断为是遮挡物，则获取它的深度值并进行累加，最后取平均得到$d_{Blocker}$。第二步则是直接用公式$(3)$计算半影大小，第三步根据半影大小进行PCF滤波。这里贴一下核心的实现代码。

float findBlocker( sampler2D shadowMap,  vec2 uv, float zReceiver ) {
  const int radius = 40;
  const vec2 texelSize = vec2(1.0/2048.0, 1.0/2048.0);
  float cnt = 0.0, blockerDepth = 0.0;
  int flag = 0;
  for(int ns = 0;ns < BLOCKER_SEARCH_NUM_SAMPLES;++ns)
  {
      vec2 sampleCoord = (vec2(radius) * poissonDisk[ns]) * texelSize + uv;
      float cloestDepth = unpack(texture2D(shadowMap, sampleCoord));
      if(zReceiver - 0.002 > cloestDepth)
      {
        blockerDepth += cloestDepth;
        cnt += 1.0;
        flag = 1;
      }
  }
  if(flag == 1)
  {
	  return blockerDepth / cnt;
  }
  return 1.0;
}

float PCF(sampler2D shadowMap, vec4 shadowCoord, float radius) {
  const vec2 texelSize = vec2(1.0/2048.0, 1.0/2048.0);
  float visibility = 0.0, cnt = 0.0;
  for(int ns = 0;ns < PCF_NUM_SAMPLES;++ns)
  {
    vec2 sampleCoord = (vec2(radius) * poissonDisk[ns]) * texelSize + shadowCoord.xy;
    float cloestDepth = unpack(texture2D(shadowMap, sampleCoord));
    visibility += ((shadowCoord.z - 0.001) > cloestDepth ? 0.0 : 1.0);
    cnt += 1.0;
  }
  return visibility/cnt;
}

float PCSS(sampler2D shadowMap, vec4 shadowCoord){

  // STEP 1: avgblocker depth
  float avgBlockerDepth = findBlocker(shadowMap, shadowCoord.xy, shadowCoord.z);

  // STEP 2: penumbra size
  const float lightWidth = 50.0;
  float penumbraSize = max(shadowCoord.z-avgBlockerDepth,0.0)/avgBlockerDepth*lightWidth;

  // STEP 3: filtering
  return PCF(shadowMap, shadowCoord, penumbraSize);
  //return 1.0;

}

  实现的效果见本文的开头。

四、PCSS效率改进——VSSM

  相比最初的PCF阴影贴图算法，PCSS算法新增了$d_{Blocker}$的计算过程，由此需要再花费更多的对深度图的纹理访问。纹理的访问对性能的损害非常大，由此启发人们寻找更为快速的$d_{Blocker}$计算方法和快速的PCF滤波方法，VSSM（Variance Soft Shadow Mapping）由此诞生。

  PCSS的第一步和第三步本质上都是根据给定的滤波半径去查找深度纹理的深度值，都是一个类似的卷积滤波过程。第一步根据读取得到的深度值判断是否为遮挡物，如果是遮挡物则会累加其深度值，最后做加权平均，得到$d_{Blocker}$；而第三步根据计算得到的滤波半径大小，读取深度纹理值，进行可见性（即是否为遮挡物）的判断并累加，最后加权平均。第一步和第三步的区别仅在于，第一步需要对遮挡物的深度值进行加权平均（而非对滤波区域内的所有深度值进行加权平均）。因此，VSM算法尝试用同一种思路快速计算PCSS的第一步和第三步。

  我们先把关注点放在PCF滤波上，PCSS第三步的PCF滤波可以用如下的卷积公式表示：

$$V(x)=\sum_{q\in N(p)}w(p,q)\cdot \chi^+[D_{SM}(q)-D_{scene}(x)] \tag {4}$$

  其中，$V(x)$是$x$点处的可见性，$\omega(p,q)$是滤波权重函数（例如高斯权重、均值权重等），$\chi^+$函数对大于$0$的输入返回$1$，对小于$0$的输入返回$0$。$D_{SM}(q)$表示Shadow Map上$q$处的深度值，$D_{scene}(x)$则为场景中$x$处在光的视角下的深度值。直观上，公式$(4)$可以看成在滤波范围内有多少百分比的深度值超过了$x$处的深度值，而$V(x)$就是这个百分比取值，如果我们能够快速得到这个百分比，那么也就不需要循坏迭代采样滤波了！公式$(4)$的计算可以转化成等价问题：对于给定$x$处的深度值$D_{scene}(x)$，$P(D_{SM}(q)>D_{scene(x)})$概率为多少？其中$P(D_{SM}(q)>D_{scene(x)})$就等价于$V(x)$。

  为了计算$V(x)$，VSSM引入了概率论的方法。在概率论中，有如下的公式成立：

$$Var(X)=E(X^2)-E^2(X) \tag {5}$$

  即如果知道$X$和$X^2$的数学期望（或者说均值），那么我们就可以根据上述公式计算其方差。而如果知道均值$\mu$和其方差$\sigma^2$，则有如下的切比雪夫不等式（Chebychev’s inequality）成立：

$$P(x>t)\leq \frac{\sigma^2}{\sigma^2+(t-\mu)^2} \tag {6}$$

  VSSM直接把上述公式$(6)$的不等符号$\leq$当成约等符号$\approx$用，从而快速求解出$P(D_{SM}(q)>D_{scene(x)})$，这就是它的快速计算原理！但在此之前，我们需要计算给定任意一点$q$和滤波半径$r$，计算深度纹理上该范围内的深度均值和深度平方的均值。这里不需要额外新增一个pass，用深度纹理的r通道和g通道分别存储深度值和深度值的平方即可。问题在于如何计算任意一点$q$、任意滤波半径$r$大小下的两个均值$E(X^2)$和$E(X)$，关于这个问题有以下两种解决方案：

• 借助于纹理的MIPMAP机制，MIPMAP的生成过程，后一层纹理是由前一层纹理的均值降采样得到，因此可以快速得到纹理上任意一点的均值，只需根据滤波半径$r$大小去寻找对应的层级即可（两个层级之间可以再次插值提升准确度）；

图10 纹理MIPMAP

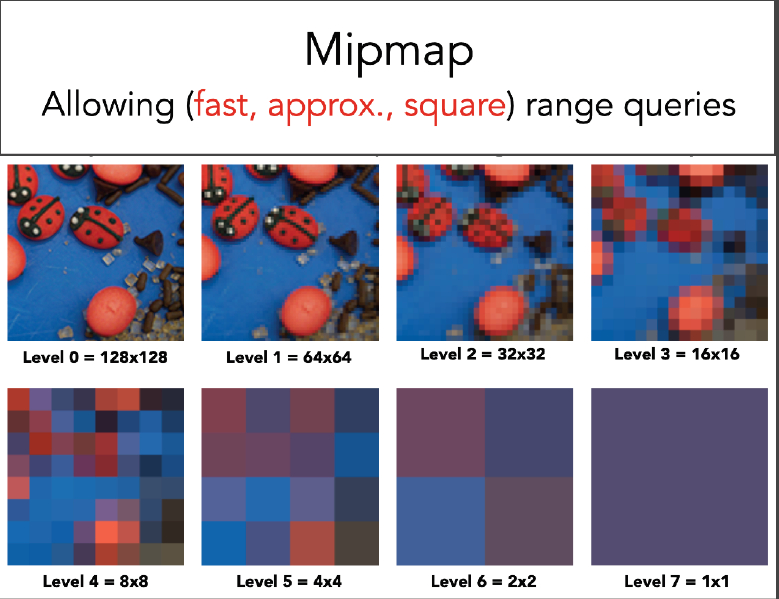
• 借助于Summed-Area table（简称SAT），即二维的面积前缀和，需要额外自己主动实现，不再赘述。

  MIPMAP直接用底层硬件可以自动生成，但MIPMAP仅仅局限于方形区域的均值查找，相比之下SAT更具优势。但无论是MIPMAP还是SAT，只要光源发生了移动、旋转等变化，那么均需要重新计算。得到的深度均值和深度平方的均值，那么就可以计算出深度方差，然后直接用公式$(6)$就可以快速近似得到PCF滤波结果。

  解决了PCF快速滤波问题，现在问题转到PCSS的第一步。我们知道，第一步计算$d_{Blocker}$并不是简单地对滤波范围内的深度值取加权平均，而是对滤波范围内的遮挡物的深度值取平均，对于那些非遮挡物我们不会累加其深度值。因此我们不能直接从MIPMAP或SAT查找得到$d_{Blocker}$。但通过公式$(6)$我们近似知道滤波范围内，$P(D_{SM}(q)>D_{scene(x)})$取值是多少，相应的$P(D_{SM}(q)D_{scene(x)})$。有以下的关系成立：

$$P(D_{SM}(q)>D_{scene}(x))\cdot z_{unocc}+P(D_{SM}(q)\leq D_{scene}(x))\cdot z_{occ}=z_{avg} \tag {7}$$

  其中$z_{avg}$是通过MIPMAP或者SAT查找得到的滤波范围的深度均值，$z_{unocc}$、$z_{occ}$分别是非遮挡物、遮挡物的深度均值，两个$P$分别对应他们的百分比。我们现在要求$z_{occ}$（即$d_{Blocker}$），但上述公式还有一个未知量$z_{unocc}$，即非遮挡物的深度均值。VSSM进一步做了个大胆的假设，直接假设$z_{unocc}$取值为$D_{scene}(x)$，即非遮挡物的平均深度刚好与$x$点处的深度值一样（在该假设下，阴影接收物是一个平面）。从而最终计算根据公式$(7)$得到$z_{occ}$。

  VSSM和PCSS的区别在于求解方法的效率，VSSM通过大胆的假设和近似实现了快速的$d_{Blocker}$计算和PCF滤波过程，避免大量的纹理访问过程，显著地提升了阴影生成效率。

五、VSSM改进——MSM

  VSSM虽然高效，但其大胆的假设和近似也带来了一些问题。VSSM的缺点主要来源于近似带来的误差。近似结果偏大，那么阴影会偏暗一点，结果尚可接受；而如果近似结果偏小，那么会导致漏光（Light Leaking）现象的产生，这是一种严重的失真（如下图11车底所示）。此外，VSSM容易在非平面阴影接收物上产生的奇怪的阴影（来源于前面提到的$z_{unocc}$的深度假设）。

图11 VSSM漏光现象

  VSSM用深度的均值$\mu$和方差$\sigma$来逼近可见性的累积分布函数（简称CDF，即前面提到的$P(D_{SM}(q)>D_{scene(x)})$），本质上就是用深度值分布的一阶原始矩和二阶中心矩。为了进一步提升近似准确率，MSM（Moment Shadow Mapping）采用了更高阶的矩来进行估算（前四阶矩）。

  在概率论中，矩（moment）是对变量分布和形态特点的一组度量。n阶矩被定义为变量的n次方与其概率密度函数（PDF）之积的积分。直接使用变量计算的矩被称为原始矩（raw moment），移除均值后计算的矩被称为中心矩（central moment）。变量的一阶原始矩等价于数学期望（expectation）、二至四阶中心矩被定义为方差（variance）、偏度（skewness）和峰度（kurtosis）。在这里，我们用纹理的四个通道分别存储$z$、$z^2$、$z^3$和$z^4$，其中指数代表几阶矩。

  MSM基于这样的一个结论：我们可以用前$m$阶矩来表示具有$m/2$个台阶的阶跃函数。对于深度值的分布估计，通常情况下四阶矩已经可以得到非常不错的结果。下图12展示了PCF与前四阶矩的拟合结果比较，理想情况下，越靠近PCF结果越好！四阶矩的逼近结果已经非常接近PCF了。

图12 PCF、2阶、3阶、4阶近似逼近的结果比较

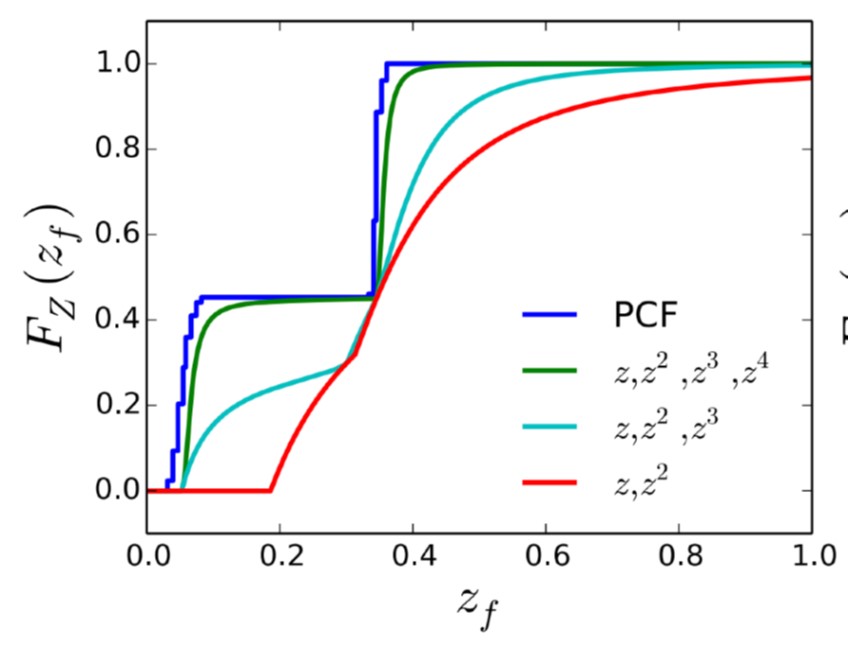
  MSM的原理比较复杂，闫老师没有仔细展开。我查了相关资料，也没有仔细看，这里仅仅解读一下实现的伪代码，如图13所示。算法的输入为存储深度$z$值前四阶矩的预过滤结果$b\in \mathbf{R}^4$、当前片元在光视角下的深度$z_{f}\in \mathbf{R}$、偏移值$\alpha >0$；算法的输出为阴影强度$G(b,z_f)$。

图13 MSM实现伪代码

  第一步对$b$做一定的偏移；第二步用Cholesky分解求解$c$；第三步求解图中所示一元二次方程，记求解结果为$z_2$和$z_3$，其中$z_2\leq z_3$。最后阴影强度$G$由如下公式给出：

$$G= \begin{cases} 0 & z_{f}\leq z_2\\ \frac{z_f\cdot z_3-b_1'\cdot(z_f+z_3)+b_2'}{(z_3-z_2)\cdot(z_f-z_2)} & z_2< z_f\leq z_3\\ 1-\frac{z_2\cdot z_3-b_1'\cdot(z_2+z_3)+b_2'}{(z_f-z_2)\cdot(z_f-z_3)} & z_3 < z_f \end{cases}$$

  图13给出了VSM与MSM的结果比较，相比于VSM，MSM的阴影估算准确了很多，额外的性能开销还尚可观。

图13 MSM实现伪代码

六、基于距离场的软阴影

  有向距离场（Signed Distance Field，简称SDF）表示为空间中的一个点到场景中所有物体表面的最近距离，其中的符号表示点在内部（负号）还是在外部（正号）。光线步进（Ray Marching）借助于SDF来感知当前位置到最近物体表面的距离，并以此作为最长的步进距离向前移动，一直步进到某个表面上或者超过给定的距离。

  基于距离场的软阴影结合了光线步进的思想，其本质上并非物理准确（比PCSS还要更fake一些），但仍然能够产生非常不错的软阴影效果。该方法在shader toy上非常常用。核心的原理如图14所示，从需要计算阴影强度的着色点出发，向光源发射一条Shadow Ray，沿着该方向进行光线步进。每步进到一个点，我们可以得到一个圆心为当前点、半径为当前点的SDF值的圆（三维情况下为球体），从出发点向该圆作一条切线，可以得到一个夹角（如图所示的$\theta_1$、$\theta_2$和$\theta_3$），取所有这些夹角中的最小值，根据这个值来确定半影大小。

图14 基于SDF的软阴影

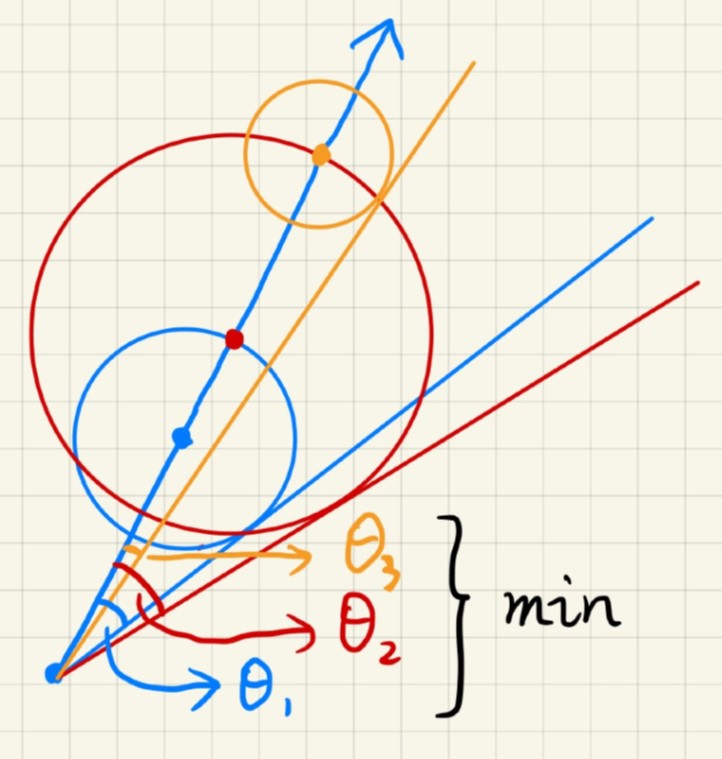
  由简单的三角关系可以的得到夹角$arcsin\frac{SDF(p)}{|p-o|}$，其中$o$为起始点，$p$为当前所在位置。这个公式计算需要用到非常耗时的反三角函数，为了避免反三角函数的开销。一个更为快速的方法是用下面的公式：

$$\min \{\frac{k\cdot SDF(p)}{|p-o|},1.0\}$$

  上述公式直接把反三角函数去掉了。上述公式的$k$为缩放系数，$k$越大，则计算得到的半影大小会越小（因为角度越大，则表示视角越大，越不在遮挡范围内），阴影越硬，正如图15所示。

图15 不同k值的阴影柔和效果比较

  基于SDF的方法能够生成比较高质量的软阴影，但它也有一个致命的缺点：需要预计算场景的SDF并存储（例如用3D纹理进行存储）。如何减小内存开销是一个非常重要的问题。除此之外，该方法容易在边界处产生一些artifact。

Reference

$[1]$ Summed-Area Variance Shadow Maps

$[2]$ Peters C, Klein R. Moment shadow mapping[C]//Proceedings of the 19th Symposium on Interactive 3D Graphics and Games. 2015: 7-14.

$[3]$ GAMES202: 高质量实时渲染