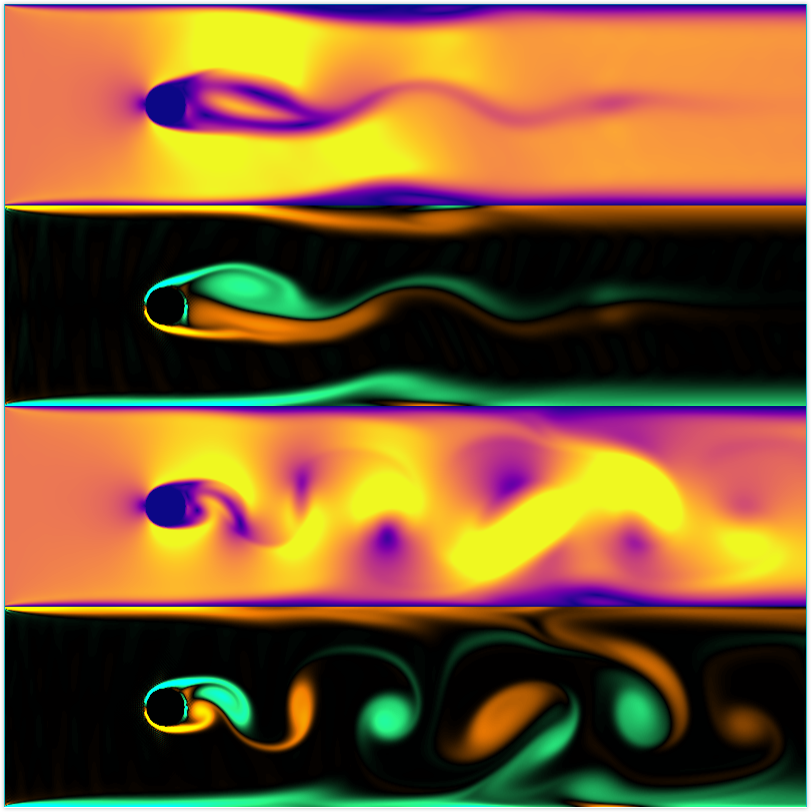
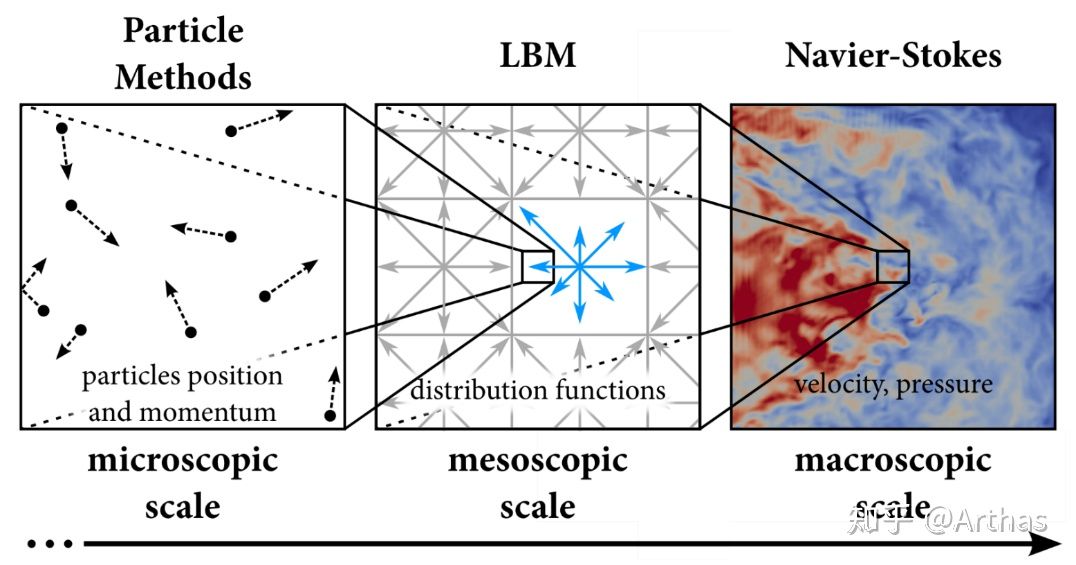
相对于基于N-S流体方程的模拟方法，栅格Boltzmann流体模拟方法（Lattice Boltzmann Method，简称LBM）是一种截然不同的流体模拟算法，表面上看起来跟Navier-Stokes没什么太大的关联，但依旧能够实现非常逼真的流体动画（特别是细粒度流体）。LBM容易理解，实现起来也不难。

  LBM方法本质上是一种基于拉格朗日视角的模拟方法，形式上却跟欧拉视角下的网格有点相似，它将微观粒子的动力学与宏观流体规律相结合，同时具有较好的精度，因此是很好的弱可压缩（甚至不可压缩）N-S方程二阶精准求解方法。在图形学领域，我们模拟的绝大部分都是不可压流体，因此契合得很好。

  LBM是一种介于宏观和微观之间的介观尺度的方法。一方面它将流体空间离散为一个个栅格，另一方面又通过栅格上的概率密度函数来描述微观尺度下的粒子分布情况。如下图所示：

一、LBM方程

  在了解LBM方程之前，有必要对LBM方法是如何规划模拟区域的。与将空间均匀划分的欧拉网格相似，LBM方法也是先均匀分割流体所在的区域，从而得到一个个小的格子。但与欧拉网格方法不同，LBM格子之间的连接方式略有不同。以三维为例，欧拉网格的格子邻居仅仅有上下、左右、前后六个，但LBM格子的邻居除了这六个之外，还可以有八个对角上的邻居，甚至可以有八个仅仅是边相连的邻居。通常用DdQq来表示某种LBM格子模式，其中d表示维度，q表示联通的格子数目（包含它自己）。常用的有D1Q3、D2Q9、D3Q15、D3Q19和D3Q27。这些不难理解。

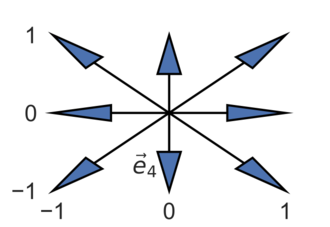
  目前我们以D2Q9即二维的LBM为例。每个LBM格子与9个格子相连（上下左右，以及四个corner，还有自身），相应的我们有9个速度方向，这些速度方向指向连通的格子，例如下面的九个，每个方向我们记为$c_i$, 其中$i=0,…,8$：

1
[0, 0], [1, 0], [0, 1], [-1, 0], [0, -1], [1, 1], [-1, 1], [-1, -1], [1, -1]

  每个LBM格子中心存储粒子分布函数$f$，用以描述流体粒子的分布情况。$f$是一个关于空间位置$x$和时间轴$t$的函数，写作$f(x,t)$。需要注意的是，粒子分布函数在每个方向上都有一个，因此一个LBM格子的有$9$个粒子分布函数，记为$f_i(x,t)\ , i=0,…,8$，分别对应每个速度方向上的粒子分布情况，这里说的粒子仅仅是概念上的虚拟粒子。

  有了上述的栅格粒子分布函数，如何得到流场的速度场？一般通过下面的公式来得到流体的速度场$u(x,t)$：

  这里的$\rho(x,t)$是虚拟粒子的密度，并非流体真正的密度场。相关概念介绍得差不多了。现在来看看LBM的核心公式，LBM方法的核心可以分成两个步骤，分别是碰撞和流动，我们先来看看碰撞步骤。碰撞步骤的核心计算公式如下所示：

  上述公式使用了BGK碰撞算子（Bhatnagar Gross and Krook）。其中$\tau_f$被称为松弛时间，与运动粘度息息相关，一般来说$\tau_f$越大则模拟出来的流体表现得越粘。运动粘度$\mu$与松弛时间的关系为$\mu =c_s^2(\tau_f -\frac{\Delta t}{2})$，其中$c_s$是声波在流体中的传播速度。而上述公式中的$f_i^{eq}(x,t)$是流场平衡状态下的分布函数，它的计算公式为：

  $\omega_i$为在该方向上的权重值。碰撞步骤可以理解为处理流体粒子的碰撞，使得流体粒子碰撞之后，能够朝向平衡状态变化。碰撞之后，我们紧接着进行流动步骤，流动步骤的核心公式如下所示：

  乍一看，这个流动的公式颇有半拉格朗日对流算法的味道。上述的公式并不难理解，它本质上就是在相连的栅格之间传播$f_i(x,t)$函数值，从而形成流体流动的效果。一般情况下我们把流动和碰撞这两个步骤合在一起实现，也就是把公式$(2)$和公式$(4)$合并成下面的形式：

  公式$(5)$就是栅格Boltzmann流体模拟的核心方程，就是这么朴实无华、简单（没有偏微分）。但要实现一个完整的LBM流体解算器还需要考虑一些其他方面的东西，例如初始状态设定、边界条件处理等等。公式$(5)$也可以写成如下的等价形式：

  实现的时候我们更倾向于使用公式$(6)$，遍历所有的格子，并按照公式更新每个格子对应的值。

二、LBM解算步骤

  首先是关于系统初始状态的设定。在初始情况下（也就是$t=0$时），我们令相关变量的取值如下：

  然后在每一个时间步上进行迭代求解。每个时间步主要的迭代过程分成如下几步：

Step (1)：利用公式$(5)$进行碰撞和流动，更新每个格子每个方向上的粒子分布函数$f_i(x,t)$；

Step (2)：利用公式$(1)$计算每个格子的$\rho(x,t)$和流体的速度场$u(x,t)$

Step (3)：处理边界条件，处理流体与边界、固体的碰撞，对流体的速度场$u(x,t)$进行边界修正

  一般情况默认时间步长$\Delta t = 1$。这里提一下流体与固体的碰撞处理，一种最简单的方案就是构建一个与LBM网格一样大小的栅格数据结构，每个栅格上存储的是布尔变量。若当前格子被固体占据，则设为True，反之设为False。这样就能快速判断当前的格子是不是在固体内部，如果在固体内部则需要做进一步的修正处理。（至于如何构建这样的一个mask结构，你可以去了解一下网格体素化的概念）

  而在边界处理方面，按照处理方法的不同可分成狄拉克边界条件（Dirichlet boundary condition）和冯诺伊曼边界条件（Neumann边界）。狄拉克边界条件直接设定边界上的物理值，例如我直接令边界上的速度场为零；而冯诺伊曼边界条件通常直接设定的是物理值在边界上的偏导数值，例如设置边界上的偏导值为零，则表示该物理量在边界上不会发生任何变化，因此应该等于靠近边上的物理量值。关于这两种边界条件的细节我不再多说。

三、二维solver的实现

  这里以一个二维的LBM解算器实现为例展开相关的实现细节，主要参考了taichi论坛上的一位搞CFD大佬的代码。首先是数据结构的声明和创建。在这里我们需要为$\rho(x,t)$、$u(x,t)$、$f_i(x,t))$和固体$mask$开辟一个二维数组，其中$f_i(x,t))$需要开辟两个一样的数组，用以迭代交换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def __init__(self,
             nx, # domain size
             ny,
             niu, # viscosity of fluid
             bc_type, # [left,top,right,bottom] boundary conditions: 0 -> Dirichlet ; 1 -> Neumann
             bc_value, # if bc_type = 0, we need to specify the velocity in bc_value
             cy = 0, # whether to place a cylindrical obstacle
             cy_para = [0.0, 0.0, 0.0], # location and radius of the cylinder
             steps = 60000): # total steps to run
    self.nx = nx  # by convention, dx = dy = dt = 1.0 (lattice units)
    self.ny = ny
    self.niu = niu
    self.tau = 3.0 * niu + 0.5
    self.inv_tau = 1.0 / self.tau
    # density.
    self.rho = ti.var(dt=ti.f32, shape=(nx, ny))
    # velocity.
    self.vel = ti.Vector(2, dt=ti.f32, shape=(nx, ny))
    self.mask = ti.var(dt=ti.f32, shape=(nx, ny))
    # particle density function.
    self.f_old = ti.Vector(9, dt=ti.f32, shape=(nx, ny))
    self.f_new = ti.Vector(9, dt=ti.f32, shape=(nx, ny))
    # weights for velocity.
    self.w = ti.var(dt=ti.f32, shape=9)
    # lattice vector
    self.e = ti.var(dt=ti.i32, shape=(9, 2))
    # boundary condition.
    self.bc_type = ti.var(dt=ti.i32, shape=4)
    # boundary value if we use dirichlet boundary condition.
    self.bc_value = ti.var(dt=ti.f32, shape=(4, 2))
    # whether to place a cylindrical obstacle.
    self.cy = cy
    self.cy_para = ti.var(dt=ti.f32, shape=3)
    self.bc_type.from_numpy(np.array(bc_type, dtype=np.int32))
    self.bc_value.from_numpy(np.array(bc_value, dtype=np.float32))
    self.cy_para.from_numpy(np.array(cy_para, dtype=np.float32))
    # number of substeps.
    self.steps = steps
    # 1/36  1/9  1/36
    # 1/9   4/9  1/9
    # 1/36  1/9  1/36
    arr = np.array([ 4.0 / 9.0, 1.0 / 9.0, 1.0 / 9.0, 1.0 / 9.0, 1.0 / 9.0, 1.0 / 36.0,
        1.0 / 36.0, 1.0 / 36.0, 1.0 / 36.0], dtype=np.float32)
    self.w.from_numpy(arr)
    arr = np.array([[0, 0], [1, 0], [0, 1], [-1, 0], [0, -1], [1, 1],
                    [-1, 1], [-1, -1], [1, -1]], dtype=np.int32)
    self.e.from_numpy(arr)

  然后就是系统状态的初始化，我们给场景中加了一个原型的固体，因此在初始化的时候相应地也设置mask：

1
2
3
4
5
6
7
8
9
10
11
12
13
@ti.kernel
def init(self):
    for i, j in self.rho:
        self.vel[i, j] = ti.Vector([0.0, 0.0])
        self.rho[i, j] = 1.0
        self.mask[i, j] = 0.0
        for k in ti.static(range(9)):
            self.f_new[i, j][k] = self.f_eq(i, j, k)
            self.f_old[i, j][k] = self.f_new[i, j][k]
        if(self.cy==1):
            if ((ti.cast(i, ti.f32) - self.cy_para[0])**2.0 + (ti.cast(j, ti.f32)
                - self.cy_para[1])**2.0 <= self.cy_para[2]**2.0):
                self.mask[i, j] = 1.0

  在进行碰撞和流体之前，我们根据公式$(3)$实现平衡状态的$f_i^{eq}(x,t)$的计算：

1
2
3
4
5
6
@ti.func # compute equilibrium distribution function
def f_eq(self, i, j, k):
    eu = ti.cast(self.e[k, 0], ti.f32) * self.vel[i, j][0] + ti.cast(self.e[k, 1], 
        ti.f32) * self.vel[i, j][1]
    uv = self.vel[i, j][0]**2.0 + self.vel[i, j][1]**2.0
    return self.w[k] * self.rho[i, j] * (1.0 + 3.0 * eu + 4.5 * eu**2 - 1.5 * uv)

  然后套用前面的公式$(6)$进行碰撞和流动的处理，得到新的$f_i(x,t)$：

1
2
3
4
5
6
7
8
@ti.kernel
def collide_and_stream(self): # lbm core equation
    for i, j in ti.ndrange((1, self.nx - 1), (1, self.ny - 1)):
        for k in ti.static(range(9)):
            ip = i - self.e[k, 0]
            jp = j - self.e[k, 1]
            self.f_new[i,j][k] = (1.0-self.inv_tau)*self.f_old[ip,jp][k] + \
                                    self.f_eq(ip,jp,k)*self.inv_tau

  随后利用新的$f_i(x,t)$套用公式$(1)$计算$\rho(x,t)$和$u(x,t)$：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
@ti.kernel
def update_macro_var(self): # compute rho u v
    for i, j in ti.ndrange((1, self.nx - 1), (1, self.ny - 1)):
        self.rho[i, j] = 0.0
        self.vel[i, j][0] = 0.0
        self.vel[i, j][1] = 0.0
        for k in ti.static(range(9)):
            self.f_old[i, j][k] = self.f_new[i, j][k]
            self.rho[i, j] += self.f_new[i, j][k]
            self.vel[i, j][0] += (ti.cast(self.e[k, 0], ti.f32) *
                                  self.f_new[i, j][k])
            self.vel[i, j][1] += (ti.cast(self.e[k, 1], ti.f32) *
                                  self.f_new[i, j][k])
        self.vel[i, j][0] /= self.rho[i, j]
        self.vel[i, j][1] /= self.rho[i, j]

  最后需要对流体的属性根据边界条件和与固体的碰撞进行修正：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
@ti.kernel
def apply_bc(self): # impose boundary conditions
    # left and right
    for j in ti.ndrange(1, self.ny - 1):
        # left: dr = 0; ibc = 0; jbc = j; inb = 1; jnb = j
        self.apply_bc_core(1, 0, 0, j, 1, j)

        # right: dr = 2; ibc = nx-1; jbc = j; inb = nx-2; jnb = j
        self.apply_bc_core(1, 2, self.nx - 1, j, self.nx - 2, j)

    # top and bottom
    for i in ti.ndrange(self.nx):
        # top: dr = 1; ibc = i; jbc = ny-1; inb = i; jnb = ny-2
        self.apply_bc_core(1, 1, i, self.ny - 1, i, self.ny - 2)

        # bottom: dr = 3; ibc = i; jbc = 0; inb = i; jnb = 1
        self.apply_bc_core(1, 3, i, 0, i, 1)

    # cylindrical obstacle
    # Note: for cuda backend, putting 'if statement' inside loops can be much faster!
    for i, j in ti.ndrange(self.nx, self.ny): 
        if (self.cy == 1 and self.mask[i, j] == 1):
            self.vel[i, j][0] = 0.0  # velocity is zero at solid boundary  
            self.vel[i, j][1] = 0.0
            inb = 0
            jnb = 0
            if (ti.cast(i,ti.f32) >= self.cy_para[0]):
                inb = i + 1
            else:
                inb = i - 1
            if (ti.cast(j,ti.f32) >= self.cy_para[1]):
                jnb = j + 1
            else:
                jnb = j - 1
            self.apply_bc_core(0, 0, i, j, inb, jnb)

@ti.func
def apply_bc_core(self, outer, dr, ibc, jbc, inb, jnb):
    if (outer == 1):  # handle outer boundary
        # Dirichlet boundary condition
        if (self.bc_type[dr] == 0):
            self.vel[ibc, jbc][0] = self.bc_value[dr, 0]
            self.vel[ibc, jbc][1] = self.bc_value[dr, 1]
        # Neumann boundary condition
        elif (self.bc_type[dr] == 1):
            self.vel[ibc, jbc][0] = self.vel[inb, jnb][0]
            self.vel[ibc, jbc][1] = self.vel[inb, jnb][1]
    self.rho[ibc, jbc] = self.rho[inb, jnb]
    for k in ti.static(range(9)):
        self.f_old[ibc,jbc][k] = self.f_eq(ibc,jbc,k) - self.f_eq(inb,jnb,k) + \
                                    self.f_old[inb,jnb][k]

  把上面的过程串起来作为一个迭代，则LBM的迭代解算过程如下，后面的一些流程可视化方法这里就不提了。总的来说，LBM方法挺简单的，不用求解大规模的PDE。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def solve(self):
    gui = ti.GUI('lbm solver', (self.nx, 2*self.ny))
    self.init()
    for i in range(self.steps):
        self.collide_and_stream()
        self.update_macro_var()
        self.apply_bc()
        ##  code fragment displaying vorticity is contributed by woclass
        vel = self.vel.to_numpy()
        ugrad = np.gradient(vel[:, :, 0])
        vgrad = np.gradient(vel[:, :, 1])
        vor = ugrad[1] - vgrad[0]
        vel_mag = (vel[:, :, 0]**2.0+vel[:, :, 1]**2.0)**0.5
        ## color map
        colors = [(1, 1, 0), (0.953, 0.490, 0.016), (0, 0, 0),
            (0.176, 0.976, 0.529), (0, 1, 1)]
        my_cmap = matplotlib.colors.LinearSegmentedColormap.from_list(
            'my_cmap', colors)
        vor_img = cm.ScalarMappable(norm=matplotlib.colors.Normalize(
            vmin=-0.02, vmax=0.02),cmap=my_cmap).to_rgba(vor)
        vel_img = cm.plasma(vel_mag / 0.15)
        img = np.concatenate((vor_img, vel_img), axis=1)
        gui.set_image(img)
        gui.show()
        if (i % 1000 == 0):
            print('Step: {:}'.format(i))

Reference

$[1]$ Lattice Boltzmann methods From Wikipedia, the free encyclopedia

$[2]$ 格子玻尔兹曼方法（LBM）的学习笔记

$[3]$ 计算流体力学视角的流体求解器

$[4]$ 大道至简的LBM算法

 上一页

Computer Graphics Real-time Rendering

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 ， 总访问量为 次 。
载入天数...载入时分秒...