Physically Based Rendering：采样和重建（一）

计算机作为离散数据的计算机器，只能使用采样的手段处理连续的数据。计算图形学本质上是采用虚拟摄像机处理虚拟空间的信号数据，因此在图形领域采样的身影无所不在，如何使用采样和重建的技术合成尽可能真实、无噪声、无走样的图像是图形学的一个重要话题。

  以下的内容大部分整理自pbrt第三版的第七章——SAMPLING AND RECONSTRUCTION。

一、采样理论

  在图形渲染领域，二维的像素栅格阵列本质上就是在虚拟摄像机的成像平面上对入射辐射率做离散的采样，因此相关的采样技术可以说是图形学的重要基础技术之一。对于连续的函数或信号，采样是我们的计算机捕获这个函数或信号的方法。除此之外，对于采样得到的数据我们还需要进行重建以尽可能地还原出原始的函数或信号分布。在基于光线追踪的渲染算法中，从视角发射的一条射线就是一个采样的过程，它返回入射到这个视角方向的出射辐射率，但这仅仅是采样，如何利用采样得到的辐射率构建与原始图像尽可能相符的图片是重建的范畴（更多的涉及到图像空间的滤波技术）。

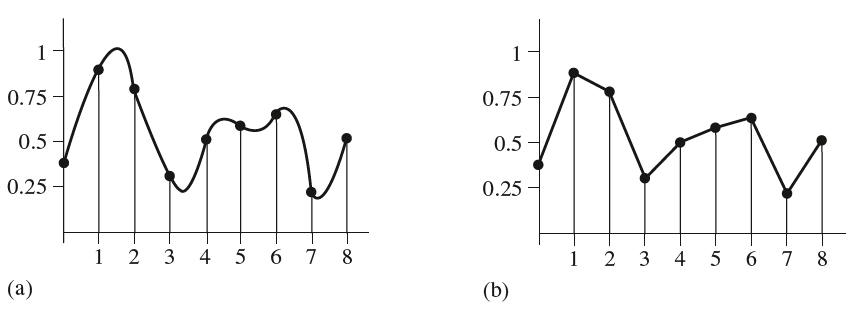
  上图给出了原始信号（左）与采样重建得到的信号（右）对比，黑色的点通过采样得到，然后在采样点之间利用线性插值的重建方法得到捕获的信号分布。可以看到，重建的结果与原始信号存在着差异，这是由采样的离散性和线性的重建引入的误差导致，这些误差在图形学中表现为锯齿和闪烁。分析和减小此类误差的手段在相关的信号处理课程中已有详细的介绍，这里只摘取了一些重点。

1、傅里叶分析

  傅里叶分析是信号处理技术的基础，大致方法就是将空间域（或时空域）的信号和函数通过傅里叶变换转变到频率域，在频率域分析相关的频谱特征。下面给出了一维的时空域和频率域互相转换的公式，它们互相构成了傅里叶变换对：

$$F(\omega)=\int_{-\infty}^{+\infty}f(x)e^{-i2\pi \omega x}dx\\ f(x)=\int_{-\infty}^{+\infty}F(\omega)e^{i2\pi\omega x}d\omega \tag {1}$$

  傅里叶变换是工科的基础，相关的细节就不赘述了。傅里叶分析中常用的一个定理就是卷积定理，卷积定理指出：空间域的卷积等价于频率域的乘积，反之亦然。即空间域的两个函数乘积等价于这两个函数的傅里叶变换形式的卷积（如下公式$(2)$），而频率域的两个函数乘积等价于这两个函数在空间域的卷积（如下公式$(3)$）：

$$\zeta \{f(x)g(x)\}=F(\omega)\otimes G(\omega) \tag {2}$$ $$\zeta(f(x)\otimes g(x))=F(\omega)G(\omega) \tag {3}$$

2、采样与重建

  常用的采样的手段是等间隔的均匀采样，即根据每隔一定间隔采样一次。这种形式的采样可以表示成一个脉冲序列与原始信号的乘积。脉冲序列由一个个单位脉冲函数构成，离散变量的单位脉冲函数$\delta (x)$定义如下：

$$\delta (x)= \begin{cases} 1, x=0\\ 0, x\neq 0 \end{cases}$$

  对于这样的单位脉冲函数，它具备如下的取样特性，它在$x=x_0$处取一次$f(x)$的函数值：

$$\displaystyle \sum_{x=-\infty}^{+\infty}f(x-x_0)\delta (x)=f(x_0)$$

  由此，脉冲序列就是由很多个$\delta (x)$组成，其数学形式如下：

$$III_T(x)=T\sum_{i=-\infty}^{\infty}\delta (x-iT) \tag {4}$$

  其中$T$是采样周期或者说采样间隔，数学形式看着有点复杂，但其实很简单。下图(b)展示了离散的脉冲序列，其采样周期为$T=1$。

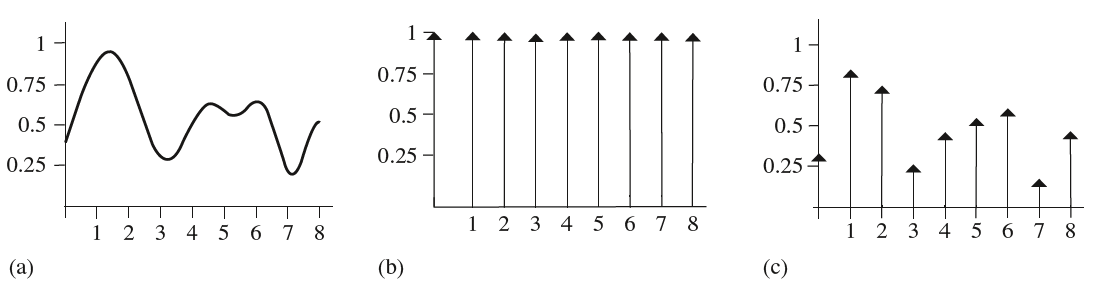
  因此，采样的过程就可以表达成采样的脉冲序列和原始信号的乘积：

$$III_T(x) f(x)=T\sum_i \delta(x-iT)f(iT) \tag {5}$$

  公式$(5)$给出了采样得到的函数值序列，这是一个一个离散的点（如上图(c)所示）。根据这些离散点，我们进行一个重建的过程以还原原始的函数分布，在空间域我们对这些采样点进行卷积得到重建的结果（其实就是滤波），记重建的函数分布为$\hat f(x)$：

$$\hat f(x)=(III_I(x)f(x))\otimes r(x) \tag {6}$$

  $r(x)$是卷积权重函数。事实上，根据卷积定理，我们可以知道采样的信号在频率的分布情况，公式$(5)$可以转换成频率域的卷积形式，卷积的函数分别是$F(\omega)$和脉冲序列函数的傅里叶形式，脉冲序列函数在频率域依旧是一个脉冲序列，只不过它的采样周期变成了$1/T$。在频率域，$F(\omega)$和脉冲序列做卷积，得到的结果就是$F(\omega)$在每个采样脉冲点上都有一份相同的拷贝。下图(c)是原始信号的傅里叶形式（即$F(\omega)$，图(a)是$F(\omega)$与频率域的脉冲序列做卷积的结果，每一个脉冲点上均有$F(\omega)$的一份拷贝，他们之间的间隔就是脉冲间隔$1/T$。

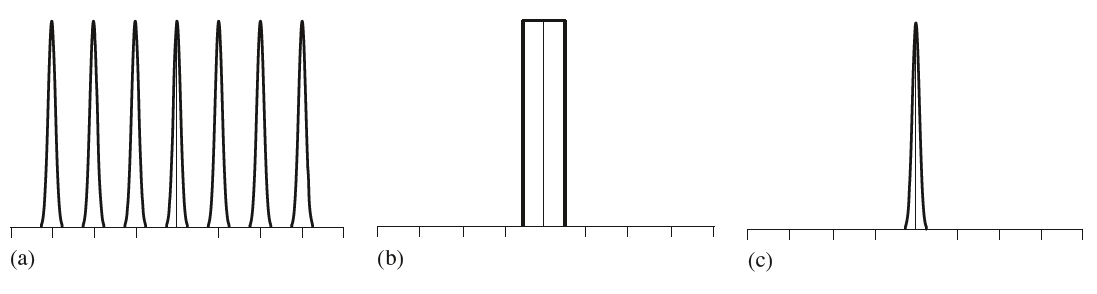
  在理想的情况下，在频率域，我们只需要获取一份$F(\omega)$即可，因此设计一个滤波器$\prod_T(\omega)$如上图(b)所示，将其与采样得到的傅里叶形式（即上图(a)）相乘，试图得到原始信号的傅里叶分布（即上图(c)）。这个过程可以描述为如下的形式：

$$\hat F(\omega)=(F(\omega)\otimes III_{1/T}(\omega)) \prod_T(\omega) \tag {7}$$

  上述的公式$(7)$与公式$(6)$殊途同归、遥相呼应，公式$(6)$给出了空间域下的采样重建过程，得到$\hat f(x)$，而公式$(7)$则给出了频率域的表达形式，得到$\hat F(\omega)$。$\hat f(x)$和$\hat F(\omega)$是采样信号分别在空间域和频率域的不同形式，它们通过卷积定理联系起来。因此，理想的采样和重建的过程可以总结为，在空间域中，对信号做一个均匀的采样，然后对采样得到的数据序列做一个卷积（在图形学中，一个常用的卷积核就是box滤波，即对周围的邻域采样值取平均）。

  目前我们的讨论都是假设$F(\omega)$是一个带限（band limit）函数，即它在频率的自变量（也就是频率）是有上界的，即定义域范围是有限的（通常由$[-u_{max},+u_{nax}]$表示）。超出该定义域范围的$F(\omega)$取值为$0$，代表$f(x)$没有该频率的分量。从现实意义上说，即一个信号的频率是有最大频率的。

  值得一提的是，空间域中采样间隔为$T$的脉冲序列，对应到频率域，其采样间隔变成了$1/T$。这是一个反比关系，即如果空间域采样间隔越小，采样越密集，则频域下的采样间隔越大（因此越能扩展到更高的频率范围，从而捕获更多的高频信息）。

3、走样现象（Aliasing）

  前面我们假设待采样的信号是带限的，但在图形学中仅有很少函数分布是带限的，大部分都拥有无穷的频率范围。对一个非带限函数采样或着使用过低的采样频率（对应就是使用较宽的采样间隔）进行采样时，将不可能避免地使得重建出来的函数分布与原始的函数分布相差甚远，这种现象被称为走样（aliasing）。

  这种现象的产生原因不难理解，以过低的采样频率为例子。采样频率过低意味着使用了很宽的采样间隔$T$，转换到频率域，则其对应的频率域周期$1/T$过低，使得原本互不重叠的采样分布重叠了，正如下图图(a)所示。

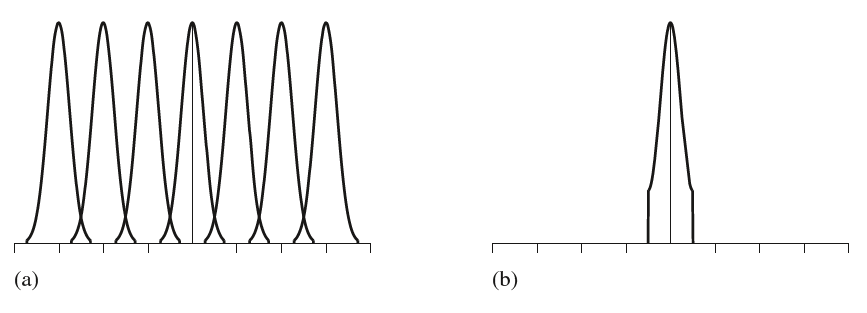
  由此重叠产生的效应我们称之为混淆。我们再对上图(a)的频谱分布进行一个带通滤波，将得到上图$(b)$的结果，这个就是重建得到的结果。相比于原始的频谱分布，它的两端被切掉了，丢失了高频部分的信息，从而产生了走样现象。由此为了避免产生明显的走样现象，一种暴力的方法就是提高我们的采样频率，降低采样间隔，但盲目地提高采样率不可取。

  理想情况下，我们的目标就是使得上图(a)中的函数刚刚好互不重叠即可。奈奎斯特采样定理给出了理想采样频率与待采样的原始信号频率之间的关系，即采样的频率至少应该为采样信号中的最大频率的两倍才不至于丢失采样信号中的信息，才能够完美地重建出原始的信号分布。这个定理我们可以从两个方面看：一是给定一个采样频率，则我们能够完美捕获的最大信号频率是采样频率的一半；另一方面则是若已知信号的最大频率，则可以以最大频率的两倍作为采样频率进行采样以完美重建原始的信号。采样频率低于定理给出的频率则是欠采样，超出了则是过采样，最理想的情况就是刚刚好，即临采样。

4、反走样技术

  针对走样现象，目前已经有诸多的反走样技术，下面介绍三大类反走样技术。在采样阶段产生的失真我们称之为前走样（prealiasing），在重建阶段产生的失真被称为后走样（postaliasing）。

（1）、非均匀采样

  顾名思义，在均匀采样的基础上对采样的间隔做一个随机扰动，使得采样的间隔不再是均匀分布。记$\zeta$为$[0,1]$的随机数，则一个非均匀的脉冲采样序列定义为：

$$\sum_{i=-\infty}^{\infty} \delta(x-(i+\frac12-\zeta)T)$$

  上面的公式就是在原来的基础上加了$\frac12-\zeta$，它的取值范围是$[-\frac12,+\frac12]$，即在一个周期内随机扰动。对于采样频率过低的情况，均匀采样和非均匀采样均会产生错误的结果，只不过非均匀采样产生的噪声而非走样现象。对于人类视觉系统，噪声更容易被接收一些。

（2）、自适应采样

  这里的自适应针对的是原始信号频域的适应，注意到一般信号有高频和低频部分。对于低频部分，没必要使用很高的采样率去采样；而对于高频分布，则应该提高采样频率以防走样的产生。这项技术的初衷非常好，但比较难适用到现实中，因为通常情况下待采样的信号分布我们并不知晓。一些技术通过上两次的采样值对当前的信号频率进行评估，如果值差异过大则适当地提高采样频率。这种方法效果依旧不是很好。

（3）、预滤波技术

  预滤波技术从产生问题的根源着手。既然在较低采样率的情况下难以捕获高频信息导致了走样的产生，那么直接在采样之前想办法去掉高频信息。此类技术直接在采样之前对信号执行一个滤波操作，这个滤波采用的滤波核通常是一个低通滤波器，目的是去掉高频、保留低频。这种方法迫使原始的信号分布在一个较低频的范围之内，避免了走样的产生。但附带的结果就是原始信号中的高频信息丢失，信号更加平滑、更加模糊了。相对于走样来说，模糊更能够被人接受一些。

5、渲染中的采样

  基于光线追钟的渲染算法本质上就是对场景的辐射率进行采样和重建的过程。场景中的辐射率是一个关于像素位置$(x,y)$、时间$t$、透镜采样点$(u,v)$和光线采样值$i_1,i_2,…$的高维函数：

$$f(x,y,t,u,v,i_1,i_2,...)\to L \tag {8}$$

  如何对这些维度进行高效、高质量的采样和重建是光线追踪渲染中永恒不变的话题。在图形渲染中，产生走样的源头主要有场景的几何体（边缘锯齿现象）、纹理和材质（摩尔纹和闪烁现象）和阴影等。这些源头是渲染的重要组成成分，因此不可能直接丢弃。最后需要提的一点就是二维阵列中的像素本质上是一个离散的采样点，它并没有面积这个概念。

二、采样器接口

  前面已经提到，光线追踪渲染器通常需要对一个$n$维的空间进行采样，因此一个采样点可以表示成$n$维向量。每个维度在$[0,1)$上随机采样，采样空间序列也可以写成$[0,1)^n$。具体多少维，取决于渲染的积分器。一种最简单的随机采样方法就是随机均匀采样，但这种方法往往需要很多的采样数量才能使得渲染积分收敛到正确的结果。在相同采样数量下，我们寻求尽可能好和高效的采样方法。

  对于生成的采样向量的用途，我们规定，采样向量的前$5$维用于摄像机（分别是单个像素内的偏移量$(x,y)$、摄像机时间$t$和透镜光圈上的随机采样$(u,v)$）。采样向量剩余维度的数据用于光线追踪过程中的采样。

1、采样质量评估：差异性

  对于高维的采样向量的质量评估，傅里叶分析已经满足不了。为此，数学家们提出了一种高维采样质量的评估策略——差异性（discrepancy）。对于一个分布良好的采样序列，它应该具备低差异性的评判标准。$n$维空间$[0,1)^n$的采样序列的差异性评估方法为：寻找$[0,1)^n$的任意一个子空间，使得散落在这个子空间内的采样点数量占总采样点数量的比值与这个子空间占总空间的比值的差最大。理想情况下，最优的采样策略应该是这两个比值相等，即差异性为零。因此，我们的目的就是寻找使得差异性尽可能小的采样模式。

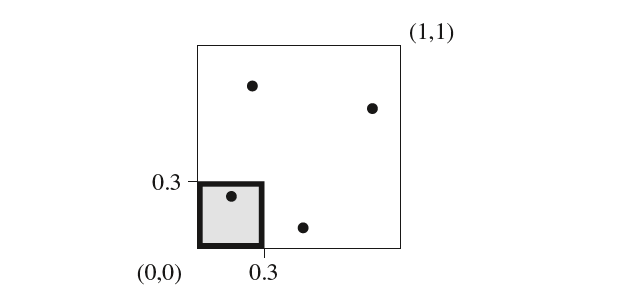
  差异性的计算定义如下，首先从采样空间的$[0,1)^n$的一个子空间$B$开始，例如下面这个：

$$B=\{[0,v_1]\times[0,v_2]\times...\times[0,v_n]\}$$

  其中$0\leq v_i < 1$。对于给定的采样点序列$P=x_1,…,x_N$，则该采样点集相对于子空间$B$的差异性为：

$$D_N(B,P)=sup_{b\in B}|\frac{\#\{x_i\in b\}}{N}-V(b)|$$

  其中$#\{x_i\in b\}$为采样点散落到子空间$b$的采样点数量，$V(b)$是子空间的体积。上面的符号$sup$应该是$max$的意思。差异性的计算一般需要数值方法来近似求解，很少能够直接求解析解。差异性的主旨思想就是衡量采样点的分布情况，如果分布得不是很均匀，那么其差异性将会很高。

  当然差异性得评估标准也有缺点：一些低差异性的点集内部可能会出现一些点过于聚集。这是低差异性的评估方法的固有缺陷导致。由此衍生了另一种评估方法，计算采样点集中任意两个采样点之间的最小距离，这个最小距离一般是越大越好。泊松圆盘采样（Poisson disk sampling）就是就是基于此评判标准进行采样的。但在实际的用途中，尽管泊松圆盘采样得到的采样点分布质量很高，但是其效率远低于低差异性的采样方法，因此用的比较少。

2、Sampler接口

  在光追渲染器中，我们首先创建一个基本的采样器基类，声明一些通用的接口以供不同的采样策略进行复用。采样器基类如下所示：

// Sampler Declarations
class Sampler {
  public:
    // Sampler Interface
    virtual ~Sampler();
    Sampler(int64_t samplesPerPixel);
    virtual void StartPixel(const Point2i &p);
    virtual Float Get1D() = 0;
    virtual Point2f Get2D() = 0;
    CameraSample GetCameraSample(const Point2i &pRaster);
    void Request1DArray(int n);
    void Request2DArray(int n);
    virtual int RoundCount(int n) const { return n; }
    const Float *Get1DArray(int n);
    const Point2f *Get2DArray(int n);
    virtual bool StartNextSample();
    virtual std::unique_ptr<Sampler> Clone(int seed) = 0;
    virtual bool SetSampleNumber(int64_t sampleNum);
    int64_t CurrentSampleNumber() const { return currentPixelSampleIndex; }

    // Sampler Public Data
    const int64_t samplesPerPixel;

  protected:
    // Sampler Protected Data
    Point2i currentPixel;
    int64_t currentPixelSampleIndex;
    std::vector<int> samples1DArraySizes, samples2DArraySizes;
    std::vector<std::vector<Float>> sampleArray1D;
    std::vector<std::vector<Point2f>> sampleArray2D;

  private:
    // Sampler Private Data
    size_t array1DOffset, array2DOffset;
};

  samplesPerPixel存储每个像素需要的采样数量，currentPixel存储当前正在进行采样的像素坐标，而currentPixelSampleIndex指明当前进行到第几个采样。某一些应用场景可能会一次性要求获取当前采样向量中的$m$个一维或两维向量，由此，我们声明下面的几个变量：

std::vector<int> samples1DArraySizes, samples2DArraySizes;
std::vector<std::vector<Float>> sampleArray1D;
std::vector<std::vector<Point2f>> sampleArray2D;
size_t array1DOffset, array2DOffset;

  这里以1D为例。samples1DArraySizes存储每个$m$的大小（因为可能有多个不同数量的一次性请求），然后sampleArray1D存储相应数量的采样点，array1DOffset辅助采样点的获取。然后使用下面的函数进行初始化：

void Sampler::Request1DArray(int n) {
    CHECK_EQ(RoundCount(n), n);
    samples1DArraySizes.push_back(n);
    sampleArray1D.push_back(std::vector<Float>(n * samplesPerPixel));
}

  上面的RoundCount用于某些特殊的采样算法对$n$进行调整，例如要求$n$是$2$的幂次方。每次获取sampleArray1D对应的采样序列，并使其加一：

const Float *Sampler::Get1DArray(int n) {
    if (array1DOffset == sampleArray1D.size()) return nullptr;
    CHECK_EQ(samples1DArraySizes[array1DOffset], n);
    CHECK_LT(currentPixelSampleIndex, samplesPerPixel);
    return &sampleArray1D[array1DOffset++][currentPixelSampleIndex * n];
}

  提供一个GetCameraSample方便直接获取摄像机要用到的采样值：

CameraSample Sampler::GetCameraSample(const Point2i &pRaster) {
    CameraSample cs;
    cs.pFilm = (Point2f)pRaster + Get2D();
    cs.time = Get1D();
    cs.pLens = Get2D();
    return cs;
}

  每使用完一个采样点，则调用StartNextSample转换到下一个采样点：

bool Sampler::StartNextSample() {
    // Reset array offsets for next pixel sample
    array1DOffset = array2DOffset = 0;
    return ++currentPixelSampleIndex < samplesPerPixel;
}

  而SetSampleNumber允许我们根据给定的参数sampleNum跳到第sampleNum采样点：

bool Sampler::SetSampleNumber(int64_t sampleNum) {
    // Reset array offsets for next pixel sample
    array1DOffset = array2DOffset = 0;
    currentPixelSampleIndex = sampleNum;
    return currentPixelSampleIndex < samplesPerPixel;
}

  最后，使用采样器的接口进行采样的过程大致如下：

sampler->StartPixel(p);
do {
    Float v = a(sampler->Get1D());
    v += b(sampler->Get1D());
    v += c(sampler->Get1D());
} while (sampler->StartNextSample());

3、PixelSampler接口

  我们首先继承采样器接口类实现一个PixelSampler，这个PixelSampler就是逐像素的采样器。每一次在指定的像素位置上，一次性生成指定数量的采样点，然后再逐个获取生成的采样点进行相关的采样计算过程。

class PixelSampler : public Sampler {
  public:
    // PixelSampler Public Methods
    PixelSampler(int64_t samplesPerPixel, int nSampledDimensions);
    bool StartNextSample();
    bool SetSampleNumber(int64_t);
    Float Get1D();
    Point2f Get2D();

  protected:
    // PixelSampler Protected Data
    std::vector<std::vector<Float>> samples1D;
    std::vector<std::vector<Point2f>> samples2D;
    int current1DDimension = 0, current2DDimension = 0;
    RNG rng;
};

  构造函数中的nSampledDimensions用于指定采样向量的最大维度。samples1D和samples2D分别存储采样点，每一维度存储samplesPerPixel个生成好的采样数据。以1D为例，索引方式为samples1D[current1DDimension][currentPixelSampleIndex]：

PixelSampler::PixelSampler(int64_t samplesPerPixel, int nSampledDimensions)
    : Sampler(samplesPerPixel) {
    for (int i = 0; i < nSampledDimensions; ++i) {
        samples1D.push_back(std::vector<Float>(samplesPerPixel));
        samples2D.push_back(std::vector<Point2f>(samplesPerPixel));
    }
}

  因此Get1D函数定义如下，它每次获取一个一维的采样数据，超出预设的最大维度下标，则返回均匀随机数，成员变量rng是随机数生成器（random number generator）：

Float PixelSampler::Get1D() {
    CHECK_LT(currentPixelSampleIndex, samplesPerPixel);
    if (current1DDimension < samples1D.size())
        return samples1D[current1DDimension++][currentPixelSampleIndex];
    else
        return rng.UniformFloat();
}

4、GlobalSampler接口

  除了逐像素一次性生成的采样方法，还有一些其他的采样算法是在整个图像空间生成采样，然后将采样点播撒到图像中的像素上。也就是连续生成的采样不再是全部由单个像素占有并使用，而是一个个地分发到不同的像素上。以下图一类采样算法生成的采样序列为例，中间一列给出了生成的前二维采样序列，考虑$2\times 3$大小的图像，这些前二维采样值乘上图像的分辨率得到相应的像素采样坐标（向下取整）。

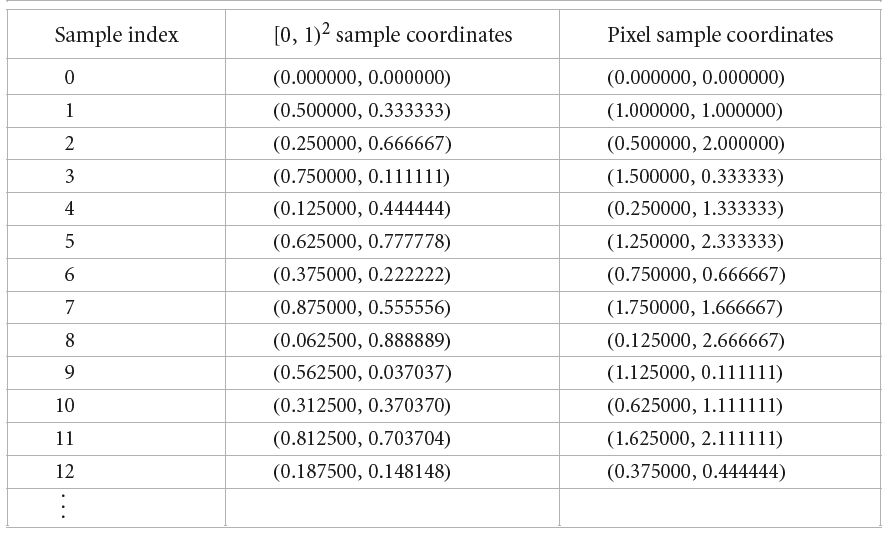
  可以看到在该采样算法中，采样索引为$0$、$6$、$12$的采样点对应着$(0,0)$这个像素坐标，其他依次类推。GlobalSampler的一些接口和通用函数声明如下所示：

class GlobalSampler : public Sampler {
  public:
    // GlobalSampler Public Methods
    bool StartNextSample();
    void StartPixel(const Point2i &);
    bool SetSampleNumber(int64_t sampleNum);
    Float Get1D();
    Point2f Get2D();
    GlobalSampler(int64_t samplesPerPixel) : Sampler(samplesPerPixel) {}
    virtual int64_t GetIndexForSample(int64_t sampleNum) const = 0;
    virtual Float SampleDimension(int64_t index, int dimension) const = 0;

  private:
    // GlobalSampler Private Data
    int dimension;
    int64_t intervalSampleIndex;
    static const int arrayStartDim = 5;
    int arrayEndDim;
};

  这里有两个关键的接口辅助此类采样器的实现：

virtual int64_t GetIndexForSample(int64_t sampleNum) const = 0;
virtual Float SampleDimension(int64_t index, int dimension) const = 0;

  GetIndexForSample输入采样点的索引sampleNum，根据当前的像素坐标currentPixel返回全局采样索引值（即上图中的sample index）。以上图为例，若当前像素坐标为(0,2)，sampleNum=0，则该接口应该返回第一个出现的对应的像素坐标值为(0,2)的采样的全局索引即2。同理GetIndexForSample(1)应返回8。这里sampleNum是相对于当前像素的采样索引，即当前像素的第一个采样、第二个采样，依次类推。

  而SampleDimension获取全局采样索引index（即上面接口的输出）和要查询的第几维度dimension，返回对应的采样值相对于其所在像素的偏移量。依旧以上图为例，SampleDimension(4,1)返回值为0.333333，首先根据全局采样索引4找到对应的采样向量(0.125000, 0.444444)，乘以图像分辨率得到(0.250000, 1.33333)，减去其对应的像素坐标(0,1)，得到偏移量(0.250000, 0.33333)，然后因为dimension为1，所以返回0.33333。

  尽管是全局生成了所有像素的所有采样点，但是在使用的时候还是逐个像素使用该像素应有的采样点，这需要一些技巧找到给定像素的所有采样点。dimension用于记录当前像素将要获取的当前采样向量中的下一个维度的索引，intervalSampleIndex记录当前采样向量的全局索引。在初始时，我们需要从全局的采样点中获取当前像素应有的采样点，保存到基类的sampleArray1D和sampleArray2D当中：

void GlobalSampler::StartPixel(const Point2i &p) {
    Sampler::StartPixel(p);
    dimension = 0;
    intervalSampleIndex = GetIndexForSample(0);
    // Compute _arrayEndDim_ for dimensions used for array samples
    arrayEndDim =
        arrayStartDim + sampleArray1D.size() + 2 * sampleArray2D.size();

    // Compute 1D array samples for _GlobalSampler_
    for (size_t i = 0; i < samples1DArraySizes.size(); ++i) {
        int nSamples = samples1DArraySizes[i] * samplesPerPixel;
        for (int j = 0; j < nSamples; ++j) {
            int64_t index = GetIndexForSample(j);
            sampleArray1D[i][j] = SampleDimension(index, arrayStartDim + i);
        }
    }

    // Compute 2D array samples for _GlobalSampler_
    // ...
}

  arrayStartDim和arrayEndDim记录那些需要一次性获取多个一维或二维采样值的下标起始，例如sampleArray1D[arrayStartDim]到arrayStartDim[arrayEndDim]之间的数组保存着这样的采样值。sampleArray1D[0]到sampleArray1D[arrayStartDim]之间保存着用于摄像机的五个维度的采样。而arrayStartDim[arrayEndDim]之后的保存着一次只获取一个一维的采样值。

  值得注意的是sampleArray1D依旧保存的是那些需要一次性获取多个一维采样值，而对于那些一次只获取一个采样值的，我们依旧从全局采样点集中动态获取，2D同理：

Float GlobalSampler::Get1D() {
    ProfilePhase _(Prof::GetSample);
    if (dimension >= arrayStartDim && dimension < arrayEndDim)
        dimension = arrayEndDim;
    return SampleDimension(intervalSampleIndex, dimension++);
}

Point2f GlobalSampler::Get2D() {
    ProfilePhase _(Prof::GetSample);
    if (dimension + 1 >= arrayStartDim && dimension < arrayEndDim)
        dimension = arrayEndDim;
    Point2f p(SampleDimension(intervalSampleIndex, dimension),
              SampleDimension(intervalSampleIndex, dimension + 1));
    dimension += 2;
    return p;
}

三、完全随机采样

  完全随机采样是一种基本的采样方法之一，虽然效果不佳，但是通常被用于与其他的采样方法进行比较，因此有必要创建一个完全随机的采样器。完全随机的采样器很简单，使用随机数生成器直接生成即可：

class RandomSampler : public Sampler {
  public:
    RandomSampler(int ns, int seed = 0);
    void StartPixel(const Point2i &);
    Float Get1D();
    Point2f Get2D();
    std::unique_ptr<Sampler> Clone(int seed);

  private:
    RNG rng;
};

RandomSampler::RandomSampler(int ns, int seed) : Sampler(ns), rng(seed) {}

Float RandomSampler::Get1D() {
    ProfilePhase _(Prof::GetSample);
    CHECK_LT(currentPixelSampleIndex, samplesPerPixel);
    return rng.UniformFloat();
}

Point2f RandomSampler::Get2D() {
    // ...
}

void RandomSampler::StartPixel(const Point2i &p) {
    ProfilePhase _(Prof::StartPixel);
    for (size_t i = 0; i < sampleArray1D.size(); ++i)
        for (size_t j = 0; j < sampleArray1D[i].size(); ++j)
            sampleArray1D[i][j] = rng.UniformFloat();

    for (size_t i = 0; i < sampleArray2D.size(); ++i)
        for (size_t j = 0; j < sampleArray2D[i].size(); ++j)
            sampleArray2D[i][j] = {rng.UniformFloat(), rng.UniformFloat()};
    Sampler::StartPixel(p);
}

  完全随机的采样方法拥有简单、高效的优点，但其缺点也十分明显。完全随机生成的采样点很容易出现某些采样空间播撒的采样点很少（欠采样）、而另外一些采样空间播撒的采样点很密集（过采样），因此为了能够收敛到正确的结果往往需要生成大量的采样点。

Reference

$[1]$ M, Jakob W, Humphreys G. Physically based rendering: From theory to implementation[M]. Morgan Kaufmann, 2016.