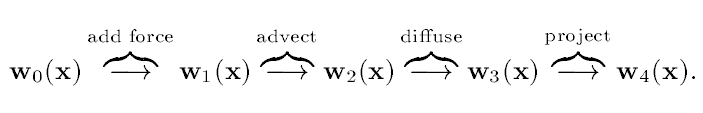基于粒子与基于网格的流体模拟算法是计算机图形学中的流体模拟界的两大算法框架，这两种算法分别对应了物理模拟中的两个视角：拉格朗日视角和欧拉视角。与基于粒子的拉格朗日流体模拟解然不同，基于欧拉网格的流体模拟采用了完全不同的算法策略，它不再关注随着物理规律运动的流体粒子，而将目光转向空间中的一组固定的网格点。
基于粒子与基于网格的流体模拟算法是计算机图形学中的流体模拟界的两大算法框架，这两种算法分别对应了物理模拟中的两个视角：拉格朗日视角和欧拉视角。与基于粒子的拉格朗日流体模拟解然不同，基于欧拉网格的流体模拟采用了完全不同的算法策略，它不再关注随着物理规律运动的流体粒子，而将目光转向空间中的一组固定的网格点。流体模拟的这两种算法各有利弊，其中基于欧拉网格的模拟方法可以实现无条件稳定，这是基于粒子的模拟方法所不能及的。目前已经有人提出了两种方法结合的模拟策略，这里暂且不说。**相比于基于粒子的模拟方法，无论是从理论上还是从实现上，基于欧拉网格的模拟方法要复杂得多**。
## 一、基于欧拉网格的流体模拟
首先来看基于欧拉网格的流体模拟算法的整体框架，主要参考了Jos Stam$^{[1]}$的极为经典的无条件稳定的流体模拟论文。基于欧拉网格的流体模拟算法同样是围绕Navier-Stokes流体力学方程展开，只不过采用了不同的偏微分方程求解方式：
$$
\nabla \cdot u=0 \tag {1}
$$
$$
\frac{D u}{Dt}=\frac{\partial u}{\partial t}+u\cdot \nabla u=-\frac1\rho\nabla p+\mu \nabla ^2u+f \tag {2}
$$
还是熟悉的流体力学方程，其中$u$是流体的速度场，$t$为时间，$\rho$是流体密度，$\mu$是流体的粘度系数，$f$是体积力项（如重力）。$\frac{Du}{Dt}$是流体关于速度场的物质导数，在基于粒子的流体模拟中，每个粒子的加速度就是关于速度的物质导数$\frac{Du}{Dt}$，这是因为物质导数的定义就是从拉格朗日视角展开的。拉格朗日视角下的物质导数可以转换成欧拉视角下的一个形式，就是公式$(2)$中的左边$\frac{Du}{Dt}=\frac{\partial u}{\partial t}+u\cdot \nabla u$，这是因为欧拉视角下我们关注的是空间中的一个固定点，因而物质导数就变成了给定点上的速度随时间的变化率$\frac{\partial u}{\partial t}$与在流体先前的速度场作用下的变化率$u\cdot \nabla u$之和。因此，在基于欧拉网格的流体模拟方法中，我们需要计算固定点上的加速度$\frac{\partial u}{\partial t}$，将$u\cdot \nabla u$移至右边：
$$
\frac{\partial u}{\partial t}=-u\cdot \nabla u-\frac1\rho\nabla p+\mu \nabla^2u+f \tag {3}
$$
所以，相比于基于粒子的模拟方法，基于欧拉网格的模拟方法多了一项需要计算，即$-u\cdot \nabla u$，后面将会提到这一项就是**对流项**，这是粒子方法与网格方法最大的不同之处。
公式$(3)$中的压强梯度项$-\frac1\rho \nabla p$与保持流体的不可压缩性（即散度为零，公式$(1)$）密切相关，计算压强项这一步我们通常称之为投影，即将速度场投影到散度为零的空间中，从而使得流体表现出不可压缩的特性。根据Helmholtz-Hodge分解定理，给定的一个速度场$w$，可将其分解成一个散度为零的速度矢量$u$与压强标量场的梯度之和$^{[2]}$：
$$
w=u+\nabla p \tag {4}
$$
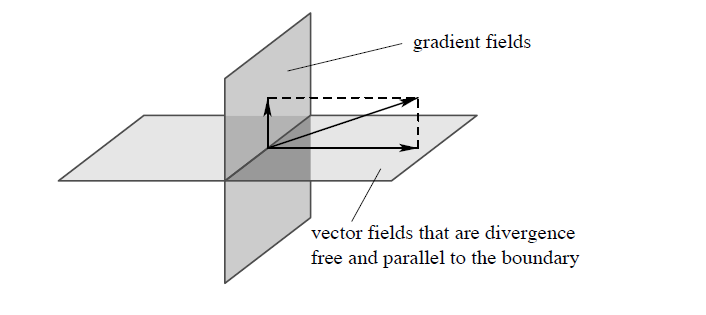
其中的$u$满足$\nabla \cdot u=0$，即散度为零，如下图1所示。为此，我们引入一个正交投影操作算子$P$，通过算子$P$将速度场$w$投影到散度为零的部分$u$，即$u=Pw$。在线性代数中，投影算子$P$有这样的一种性质，即无论投影多少次，最终都等价于只投影一次，例如$P^2=P$。故同样有$Pu=u$，因为$Pu=P(Pw)=P^2w=Pw=u$。
图1 Helmholtz-Hodge分解
将算子$P$作用到公式$(4)$两边，有：
公式$(5)$得出了$P(\nabla p)=0$，直观的意义就是经过算子$P$的作用，流体的压强梯度$\nabla p$变为零，流体处于一个不可压缩的平衡状态。现在我们将算子$P$作用到流体力学公式$(3)$的两边，消去其中的$P(\nabla p)$：
通过这个投影算子$P$，我们消去了原流体方程中的压强梯度项$-\frac1\rho \nabla p$，其实是实质上转化成了投影算子$P$，从而解释了为什么求压强梯度项的算法被称为投影 。公式$(6)$就是我们将要求解的核心方程，当然公式$(6)$其实是一个易于理解的形式，在最后做压强投影时实际上还是通过求解压强值，并将其作用到流体的速度场上来保证流体的不可压缩性。
在基于粒子的流体模拟算法中，我们将粒子的所有受力计算出来并进行叠加获取其合力，最后做一个时间积分。但是在基于欧拉网格的流体模拟中，我们是将公式$(6)$中的项拆分开来然后分步进行的，每一步的输出作为下一步的输入，依次进行，而且顺序不能乱。总的来说，需要计算的项分别是体积力项$f$，对流项$-(u\cdot \nabla u)$，粘度项$\mu \nabla^2 u$以及最后的压力投影项$-\frac1\rho \nabla p$，算法的总体流程如下图2所示：
图2 算法流程
接下来就按照图2的顺序依次展开相应的计算算法。
二、MAC网格数据结构 在展开各项的计算之前我们先要看看需要用到的一些数据结构。基于欧拉网格的流体模拟都采用了空间中固定划分的网格来承载流体的物理属性，包括一些标量场、矢量场，对于普通的标量场和矢量场，我们通常采用紧密的网格即可，每个网格点记载了当前这个点上的物理属性值，任意给定的物理属性值可以通过三线性插值得到，而且相应的梯度、散度和旋度以及拉普拉斯算子等的计算可以通过有限差分法计算得到。
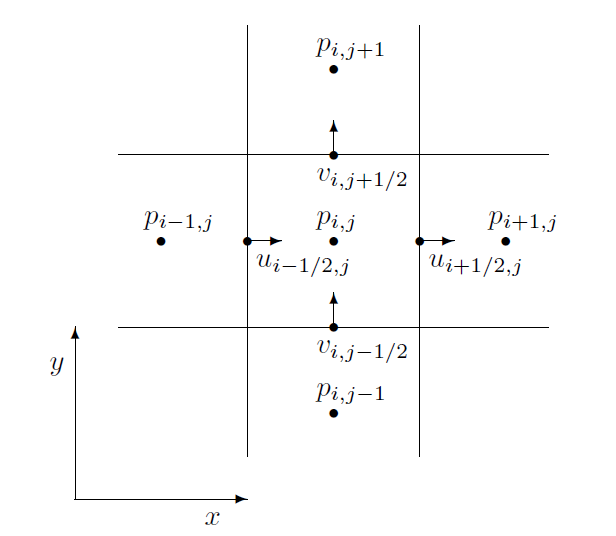
但有个特殊的矢量需要做一些不同的处理，这个矢量就是流体的速度场。对于流体的速度场矢量，我们将采用交错的MAC网格：将流体的每个分量都分离出来，每个分量存储方式如下图3所示（以二维为例）：
图3 MAC网格
上图3中的二维流体分量分别为$u$和$v$，它们不是一起存储在网格的中心处，而是分别单独存储在网格的边上，$u$分量存储在每个网格格子的垂直于$x$轴的边的中心点，$v$分量存储在每个网格格子的垂直于$y$轴的边的中心点。而普通的一些标量场（例如上图中的压强$p$、温度）和矢量场被存储在网格的中心点处。这个就是基于欧拉网格的流体模拟算法的数据分布结构。MAC网格增加了我们模拟算法实现的复杂度，但也带来了一些便利，通过MAC网格我们可以放心地采用中心差分法来做一些微分操作而不用担心普通的致密网格出现的零域（null space）问题。
采用了MAC网格存储流体的速度场后，速度场的$u$分量、$v$分量和$w$分量分别单独储存，后续求解流体方程时我们需要分别更新流体的速度场的各个分量（三个分量的更新都是类似的）。
三、边界条件处理 紧接着我们还要考虑处理流体的边界问题，这也是整个流体模拟过程中非常重要的一部分。首先是固体边界的表示，这一部分设计到如何处理流体与边界的碰撞。在欧拉网格的流体模拟方法中，最为自然的方法就是采用水平集，同样构建一个空间网格，每个网格点存储采样碰撞体的符号距离场值，下面只是整体的算法代码，关于如何计算给定物体的符号距离场函数之前已经深入了解过了，这里不再赘述。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 void GridFractionalBoundaryConditionSolver3::onColliderUpdated( const Size3& gridSize, const Vector3D& gridSpacing, const Vector3D& gridOrigin) { if (_colliderSdf == nullptr ) _colliderSdf = std ::make_shared<CellCenteredScalarGrid3>(); _colliderSdf->resize(gridSize, gridSpacing, gridOrigin); if (collider() != nullptr ) { Surface3Ptr surface = collider()->surface(); ImplicitSurface3Ptr implicitSurface = std ::dynamic_pointer_cast<ImplicitSurface3>(surface); if (implicitSurface == nullptr ) implicitSurface = std ::make_shared<SurfaceToImplicit3>(surface); _colliderSdf->fill([&](const Vector3D& pt) { return implicitSurface->signedDistance(pt); }); _colliderVel = CustomVectorField3::builder() .withFunction([&](const Vector3D& x) { return collider()->velocityAt(x); }) .withDerivativeResolution(gridSpacing.x) .makeShared(); } else { _colliderSdf->fill(kMaxD); _colliderVel = CustomVectorField3::builder() .withFunction([](const Vector3D&) { return Vector3D(); }) .withDerivativeResolution(gridSpacing.x) .makeShared(); } }
有了水平集网格，我们就通过采样流体网格点的符号距离场来判断是否在流体的内部，若值为负，则在物体的内部发生了穿透，需要做一些矫正。当然在这里并不存在显式的流体粒子，因而矫正的不是流体粒子的位置，而是每个空间网格点上的流体属性值，似乎有点抽象，其实质上还是等价于纠正了流体微团的位置。
我们将要实现的就是无通量边界条件。无通量边界条件就是碰撞不穿透约束，即在碰撞体的表面处，流体的速度场投影到表面法线方向上的值为零，这种边界条件数学上的定义为：
其中，$u$是边界处流体的速度场矢量，$n$是边界出碰撞体的单位表面法线。当然上面说的仅仅是碰撞体静止时的情况，我们还需要考虑碰撞体的移动，因此实际上要求的是流体的速度场与碰撞体的速度场的差（即相对速度）在法线方向上的投影为零：
上式中，$u_c$是表面处碰撞体的速度场矢量，$u_{rel}$记为流体与碰撞体之间的相对速度。为了使得相对速度在法线方向上的投影为零，我们可以将相对速度分解成法线方向上的向量与切面向上的向量之和，然后直接取切面上的向量，得到满足碰撞约束的相对速度$u^t_{rel}$，最后得到满足约束的流体速度场$u^n$：
碰撞体边界统一用水平集构成的符号距离场表示，因而其表面法线$n$就是其符号距离场函数的梯度向量。我们实际上处理的不单单是碰撞体表面上的流体网格点，还需要处理在物体内部的点，因而对于符号距离值为负的流体网格点均需要做以上的边界处理，其余部分保持不变，下面是以流体速度场的$u$分量为例（后面均以$u$分量为例，其余的$v$分量和$w$分量类似）：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 velocity->parallelForEachUIndex([&](size_t i, size_t j, size_t k) { Vector3D pt = uPos(i, j, k); if (isInsideSdf(_colliderSdf->sample(pt))) { Vector3D colliderVel = collider()->velocityAt(pt); Vector3D vel = velocity->sample(pt); Vector3D g = _colliderSdf->gradient(pt); if (g.lengthSquared() > 0.0 ) { Vector3D n = g.normalized(); Vector3D velr = vel - colliderVel; Vector3D velt = projectAndApplyFriction(velr, n, collider()->frictionCoefficient()); Vector3D velp = velt + colliderVel; uTemp(i, j, k) = velp.x; } else uTemp(i, j, k) = colliderVel.x; } else uTemp(i, j, k) = u(i, j, k); }); ...... u.parallelForEachIndex([&](size_t i, size_t j, size_t k) { u(i, j, k) = uTemp(i, j, k); }); template <size_t N> inline Vector<double , N> projectAndApplyFriction( const Vector<double , N>& vel, const Vector<double , N>& normal, double frictionCoefficient) { Vector<double , N> velt = vel.projected(normal); if (velt.lengthSquared() > 0 ) { double veln = std ::max(-vel.dot(normal), 0.0 ); velt *= std ::max(1.0 - frictionCoefficient * veln / velt.length(), 0.0 ); } return velt; }
上面的projectAndApplyFriction就是实现了公式$(9)$的函数代码，它负责计算投影到切面上的向量，最后还乘上了一个缩放系数，这个系数来源于我们如何处理无通量边界条件得到的切面上的速度场。通常分为两种情况：自由滑移、无滑移$^{[3]}$。自由滑移就是流体在边界处的速度场直接取值为表面切向上的速度场，无滑移就是流体在边界处的速度场直接取零而不是切向速度，这个不难理解。在这里我们考虑这两者的综合，我们考虑碰撞体的摩擦力：
公式中的$\mu$就是碰撞体表面的摩擦系数，$u_t$是前面计算得到的切向上的速度场。然后在展开整个流体的边界处理之前，我们需要做一些预处理。通常在整个欧拉网格中，只有属于流体区域的网格点的速度场才有定义，但是在边边界处理时，我们要处理的是那些碰撞体内部的速度场，因而需要根据当前流体的速度场来外推 （extrapolation）非流体区域的速度场，用于后续的边界处理，这些物体内部的流体速度场是一个虚拟的速度场。外推算法采用简单的广度优先，但是我们需要指定一个外推深度，因此采用迭代的方法，每一次的迭代表示向外推进一层。一开始我们需要创建一个标记数组marker，这个marker规模与存储速度场的大小一致，对于每一个marker，若当前的网格点在碰撞体内部，则标记为”Solid”，否则标记为”Fluid”，然后采用外推算法填充速度场数组中被标记为”Solid”的那些网格点，对于每一个”Solid“的网格点，其速度场值等于周围相邻的八个网格点中被标记为”Fluid”的速度场的平均值。以速度场的$u$分量为例，其他两个分量类似：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 auto u = velocity->uAccessor(); auto uPos = velocity->uPosition(); Array3<double > uTemp(u.size()); Array3<char > uMarker(u.size(), 1 ); Vector3D h = velocity->gridSpacing(); velocity->parallelForEachUIndex([&](size_t i, size_t j, size_t k) { Vector3D pt = uPos(i, j, k); double phi0 = _colliderSdf->sample(pt - Vector3D(0.5 * h.x, 0.0 , 0.0 )); double phi1 = _colliderSdf->sample(pt + Vector3D(0.5 * h.x, 0.0 , 0.0 )); double frac = fractionInsideSdf(phi0, phi1); frac = 1.0 - clamp(frac, 0.0 , 1.0 ); if (frac > 0.0 ) uMarker(i, j, k) = 1 ; else { Vector3D colliderVel = collider()->velocityAt(pt); u(i, j, k) = colliderVel.x; uMarker(i, j, k) = 0 ; } }); ...... extrapolateToRegion(velocity->uConstAccessor(), uMarker.constAccessor(), extrapolationDepth, u); template <typename T> void extrapolateToRegion ( const ConstArrayAccessor3<T>& input, const ConstArrayAccessor3<char >& valid, unsigned int numberOfIterations, ArrayAccessor3<T> output) { const Size3 size = input.size(); assert(size == valid.size()); assert(size == output.size()); Array3<char > valid0(size); Array3<char > valid1(size); valid0.parallelForEachIndex([&](size_t i, size_t j, size_t k) { valid0(i, j, k) = valid(i, j, k); output(i, j, k) = input(i, j, k); }); for (unsigned int iter = 0 ; iter < numberOfIterations; ++iter) { valid0.forEachIndex([&](size_t i, size_t j, size_t k) { T sum = zero<T>(); unsigned int count = 0 ; if (!valid0(i, j, k)) { if (i + 1 < size.x && valid0(i + 1 , j, k)) { sum += output(i + 1 , j, k); ++count; } if (i > 0 && valid0(i - 1 , j, k)) { sum += output(i - 1 , j, k); ++count; } if (j + 1 < size.y && valid0(i, j + 1 , k)) { sum += output(i, j + 1 , k); ++count; } if (j > 0 && valid0(i, j - 1 , k)) { sum += output(i, j - 1 , k); ++count; } if (k + 1 < size.z && valid0(i, j, k + 1 )) { sum += output(i, j, k + 1 ); ++count; } if (k > 0 && valid0(i, j, k - 1 )) { sum += output(i, j, k - 1 ); ++count; } if (count > 0 ) { output(i, j, k) = sum / static_cast <typename ScalarType<T>::value>(count); valid1(i, j, k) = 1 ; } } else valid1(i, j, k) = 1 ; }); valid0.swap(valid1); } }
通过上面的外推处理，我们可以放心地处理边界情况了。在处理完边界情况的最后，我们还需要处理欧拉网格的边界，因为我们模拟的是空间中的固定区域，因而这些固定区域的边界需要处理，默认不处理的情况下就是允许流体流出我们的模拟区域，这个时候流出去的流体不会再被考虑。当然我们也可以让流体不流出这些区域，或者指定一些开口允许流出，这个时候将边上的流体速度场设为零即可，以速度场的$u$分量为例：
1 2 3 4 5 6 7 8 9 10 11 12 if (closedDomainBoundaryFlag() & kDirectionLeft) { for (size_t k = 0 ; k < u.size().z; ++k) for (size_t j = 0 ; j < u.size().y; ++j) u(0 , j, k) = 0 ; } if (closedDomainBoundaryFlag() & kDirectionRight) { for (size_t k = 0 ; k < u.size().z; ++k) for (size_t j = 0 ; j < u.size().y; ++j) u(u.size().x - 1 , j, k) = 0 ; }
总的来说流体的边界处理流程就是：构建碰撞体的水平集$\to$根据水平集构建marker并外推速度场$\to$处理碰撞体内部的速度场$\to$模拟区域的边界处理。上面针对流体的速度场展开了具体的边界处理，但从宏观角度来说，这里的边界条件分为两种，分别是诺伊曼（Neumann）边界条件、狄拉克（Dirichlet）边界条件。
给定一个场$f$（可以是标量场，也可以是矢量场），诺伊曼边界条件是给出了量场$f$在边界处法线方向$n$上的导数等于某个具体给定的值$c$，即：
例如$c=0$，那么表示量场$f$在边界处沿着法线方向上不变。因此我们前面提到的无通量边界条件（公式$(7)$）就是诺伊曼边界条件的子集。而狄拉克边界条件非常简单，它是直接给出边界处量场$f$的取值$c$：
当公式$(12)$中的$c=0$时，就等价于前面我们提到的无滑移速度场。每一次更新速度场我们都要调用一次固体边界处理。
四、体积力项 首先来看最简单的部分——体积力项，或者说外力项。这一项主要是考虑外部的作用力，这类力不是通过接触直接作用到流体上，而是类似于隔山打牛的凌空作用，在流体模拟中主要有重力、浮力。体积力项的计算非常简单，根据牛顿定律简单地做一个前向欧拉积分即可：
外部的体积力有几种，其中最常见的就是重力，下面以重力为例：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 void GridFluidSolver3::computeExternalForces(double timeIntervalInSeconds) { computeGravity(timeIntervalInSeconds); } void GridFluidSolver3::computeGravity(double timeIntervalInSeconds){ if (_gravity.lengthSquared() > kEpsilonD) { auto vel = _grids->velocity(); auto u = vel->uAccessor(); auto v = vel->vAccessor(); auto w = vel->wAccessor(); if (std ::abs (_gravity.x) > kEpsilonD) { vel->forEachUIndex([&](size_t i, size_t j, size_t k) { u(i, j, k) += timeIntervalInSeconds * _gravity.x; }); } if (std ::abs (_gravity.y) > kEpsilonD) { vel->forEachVIndex([&](size_t i, size_t j, size_t k) { v(i, j, k) += timeIntervalInSeconds * _gravity.y; }); } if (std ::abs (_gravity.z) > kEpsilonD) { vel->forEachWIndex([&](size_t i, size_t j, size_t k) { w(i, j, k) += timeIntervalInSeconds * _gravity.z; }); } applyBoundaryCondition(); } }
计算重力对流体的速度场的作用之后，需要调用边界处理，修正固体边界处的流体速度值。事实上，在每一次更新了流体的速度场之后，都需要进行边界处理。后续的对流、粘性以及压力等等处理完后都需要处理边界情况。
五、半拉格朗日对流 接下来就是求解流体的对流项，在基于粒子的流体模拟中，对流项被自动地执行，即不需要对粒子进行对流。对流本质上就是在流体的速度场作用下，不同网格点之间传递流体微团。从拉格朗日视角来看，就是流体微团在速度场的作用下，携带流体微团在空间中移动，流体微团的一些性质（如流体微团 的密度）在移动的过程中保持不变。因而，求解关于任意一个物理量场$q$的对流项实际上求解的是下面的对流方程：
其中$u$是流体的速度场向量。在基于粒子的流体模拟中，每个流体粒子已经自动实现了$\frac{Dq}{Dt}=0$，因而省去了这一步骤。在基于欧拉网格的流体模拟中，我们关注的是空间中的固定点，因而空间中的固定点的关于物理量场$q$随时间的变化率为$\frac{\partial q}{\partial t}$，故需要求解这个变化率，并在这个变化率的作用下更新相应网格点上保存的物理量场值$q$，这一个过程就是对流（Advection）。将公式$(14)$挪项：
一种已经过时的方法就是采用有限差分法来估算$\frac{\partial q}{\partial t}$，虽然这种方法效果很差且局限性太大，但是了解它能够加深我们对流体模拟中的”稳定性“的理解。我们现在来看看基于有限差分法的逆风对流法，以一维为例：
采用有限差分法估算公式$(16)$：
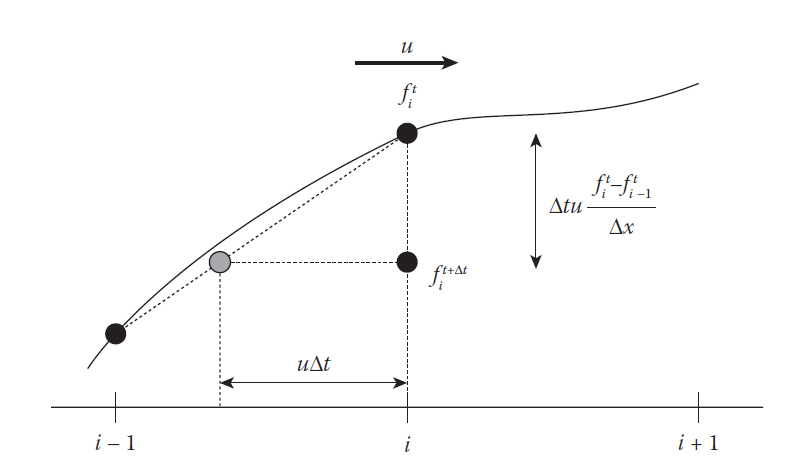
当$u>0$时我们在左边取差分，否则在右边取差分，这就是这种方法被称为”逆风”的原因。现在假设我们有一个速度$u>0$，那么根据公式$(17)$估算了$\frac{\partial q}{\partial t}$之后，再采用前向欧拉法来更新物理量场$q$，即有：
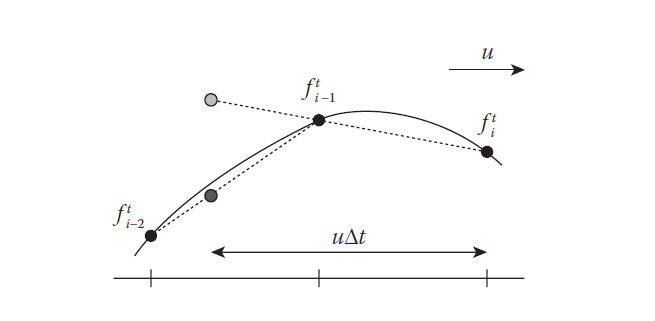
下图4很好的描述了这个对流的过程，灰色的点的$f$值就是我们更新后的量场$q$的值。
图4 1D的逆风对流法
可以看到，当我们的$u\Delta t$小于网格单元格长度$\Delta x$时，对流算法没什么问题。但是当$u\Delta t$大于$\Delta x$时，将会导致追踪了错误的灰色点，如下图5所示，正确的点应该是灰色的点下面的那个点。所以基于有限差分法的对流方法会出现不稳定的问题，归根揭底还是因为差分方法仅仅考虑了一个$\Delta x$范围内的网格点，而$u\Delta t$有可能过大导致追踪的点超出$\Delta x$的范围，基于有限差分法的对流方法仅在$u\Delta t/\Delta x<1$时保持稳定，这里的$u\Delta t/\Delta x$就是流体模拟中常说的Courant数，这种限制条件被称为Courant–Friedrichs–Lewy条件（简称为CFL条件）。在这里CFL条件的限制为1，也就是不能超过一个$\Delta x$的范围，因而使得模拟的时间步长$\Delta t$不能太大，极大地降低模拟效率。
图5 逆风对流的不稳定
目前，基于有限差分法的对流方法已经几乎不用，更多的还是采用了Jos Stam$^{[1]}$提出的无条件稳定的半拉格朗日对流算法，这种对流算法已经被证明了无条件稳定的对流算法，因而可以使用大的时间步长去模拟。这种对流算法被称为半拉格朗日对流是有原因的，它从拉格朗日视角来展开对流过程。如下图6所示，当前的每一个网格点，都可以看作是上一个时间点模拟区域中的某个流体粒子经过移动刚好落在当前的网格点，因而当前网格点（图6中的黑色点）上的物理场$q$取值应该是这个流体粒子（图6中的灰色点）的物理量场值。这个就是它的核心思想，可以看到它采用了拉格朗日的视角去解决欧拉网格对流的问题，因而被称为半拉格朗日对流。
图6 半拉格朗日对流
给定一个网格点位置为$x$，其相应的速度场为$u$，现在要计算第$n+1$个时间步长时其物理量场的取值，可以后向追踪到灰色的粒子位置为$x-\Delta tu$，然后这个粒子的物理量场的值通过周围网格点做线性插值得到，最后网格点$x$的物理量场值$q(x)^{n+1}$为：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 void SemiLagrangian3::advect( const ScalarGrid3& input, const VectorField3& flow, double dt, ScalarGrid3* output, const ScalarField3& boundarySdf) { auto outputDataPos = output->dataPosition(); auto outputDataAcc = output->dataAccessor(); auto inputSamplerFunc = getScalarSamplerFunc(input); auto inputDataPos = input.dataPosition(); double h = min3(output->gridSpacing().x, output->gridSpacing().y, output->gridSpacing().z); output->parallelForEachDataPointIndex([&](size_t i, size_t j, size_t k) { if (boundarySdf.sample(inputDataPos(i, j, k)) > 0.0 ) { Vector3D pt = backTrace(flow, dt, h, outputDataPos(i, j, k), boundarySdf); outputDataAcc(i, j, k) = inputSamplerFunc(pt); } }); }
上面的代码以标量场的对流为例，其他矢量场以及MAC网格结构的类似。backTrace函数根据当前的网格点以及速度场进行后向追踪，返回一个追踪的点（其实就是$x-\Delta tu$），然后根据这个点做一个线性插值得到新的物理量场的值。
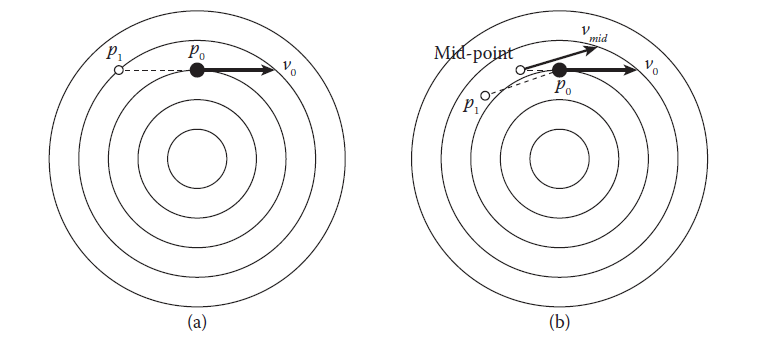
可以看到半拉格朗日对流算法通过当前的速度场进行后向追踪，最终的物理量场值是通过其所在网格点做插值得到，因而不会超出原来量场中的最大值和最小值，而且也不会受限于$\Delta tu$的大小，因而是无条件稳定的。半拉格朗日对流的实现非常简单，对于流体区域的每一个网格点的每一个物理量场，做一个公式$(19)$中的逆向追踪即可。但是存在一些准确率不高的问题，如下图7(a)所示，这是一个环形涡流，$p_0$后向追踪的点$p_1$实际上并不是上一个时间点流到$p_0$的点，因而计算的结果不准确。
图7 中点法
目前已经有许多方法来提高对流的准确性，其中一个遍是重点法。如图7(b)所示，我们后向步进半个时间步长而不是一个时间步长得到中点$p_{mid}=p_0-(\Delta t/2)v_0$，然后在重点$p_{mid}$处采样其速度场$v_{mid}$，最后采用$v_{mid}$去后向追踪$p_1=p_0-(\Delta t) v_{mid}$。通过这个简单的改动，对流算法的准确率得到了很大的提升。
然而半拉格朗日对流还存在另外一个比较严重的问题，就是数值耗散 （numerical diffusion）。我们通过后向追踪得到的点$p_1$很少会刚刚好网格点上，大多数情况都是落在网格的格子内部，这个时候我们通过线性插值来计算$p_1$对应的物理量场$q$。问题就出现在线性插值这里，当我们采用线性插值的时候我们就默认了该量场$q$在这个网格内呈线性分布，这在欧拉网格的分辨率非常高时不会有什么大的问题，但当分辨率没那么高时，就会产生可观的估算误差。网格越粗糙，误差越大。这种误差带来的影响就是流体细节（例如涡旋细节）的消失，从而影响模拟的视觉效果 。
因为这一步对流体的模拟效果非常关键，近年来，已经有不少学者针对这个数值耗散问题展开相关研究，提出了不少改进算法，有的是结合了粒子模拟方法的隐式粒子法（因为粒子法不需要对流），有的采用了一些技巧避免了插值，有的在插值方法上做一些改进，还有的采用特殊的方法还原消失在插值中的细节 。这里我们先来看针对插值方法的改进——Catmull–Rom样条插值。
简单的线性插值只获取了周围最近点的函数值信息，然后根据给定点的位置去计算相应的值。Catmull–Rom样条插值借助了更多的邻域点信息进行插值，它的函数曲线不再是一条直线，而是样条曲线。以1D为例，Catmull–Rom样条插值函数为一个三阶多项式：
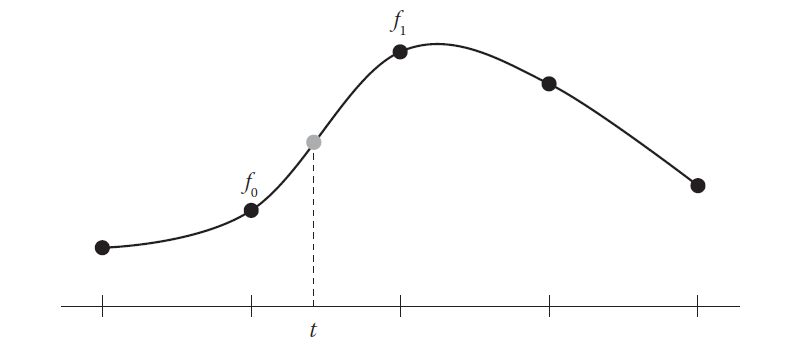
图8 Catmull–Rom样条插值
构建Catmull–Rom样条插值函数除了要知道最近点的函数值（这里就是$f_0$和$f_1$），还需要再获取另外两个点的函数值$f_{-1}$和$f_2$。令$f_{-1}、f_0、f_1、f_2$（就是图8中从左到右的四个黑色点）分别对应$t=-1、0、1、2$时的样条函数值，现在需要求解插值函数（即公式$(20)$）中的系数$a_3、a_2、a_1、a_0$，通过一些差分法以及方程联立，可得下面的方程组（$f_{-1}、f_0、f_1、f_2$均已知）：
通过公式$(21)$的方程组我可以求得全部系数，我们将传入的介于$[0,1]$之间的权重值传入插值函数并返回插值的结果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 template <typename S, typename T>inline S catmullRom (const S& f0, const S& f1, const S& f2, const S& f3, T f) S d1 = (f2 - f0) / 2 ; S d2 = (f3 - f1) / 2 ; S D1 = f2 - f1; S a3 = d1 + d2 - 2 * D1; S a2 = 3 * D1 - 2 * d1 - d2; S a1 = d1; S a0 = f1; return a3 * cubic(f) + a2 * square(f) + a1 * f + a0; }
上面我们讨论了一维的情况，二维和三维的情况只是一维的推广，这一方面与单线性插值与双线性插值、三线性插值之间的关系类似，不再赘述。但在半拉格朗日对流中直接用Catmull–Rom插值替换线性插值会带来一些问题。线性插值函数是单调的，通常是从$f_0$到$f_1$单调增或者单调减，这保证了通过插值得到的值不会超过原来的最大值也不会低于原来的最小值，但是Catmull–Rom样条插值函数不能保证它是单调的，有可能导致插值得到的值超出了原来的范围，存在不稳定的问题。为此，需要做一些修改，使之在$[0,1]$范围内变成单调函数。如下图9所示，虚线部分是原Catmull–Rom样条函数，而实线部分就是修改后的函数曲线。记$D1$为$f_1-f_0$，$d_0=(f_1-f_{-1})/2$，$d_1=(f_2-f_1)/2$，这里$d_1$、$d_2$是$f’(0)$、$f’(1)$的差分近似，使之：
图9 单调的Catmull–Rom样条插值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 template <typename T>inline T monotonicCatmullRom (const T& f0, const T& f1, const T& f2, const T& f3, T f) T d1 = (f2 - f0) / 2 ; T d2 = (f3 - f1) / 2 ; T D1 = f2 - f1; if (std ::fabs (D1) < kEpsilonD) d1 = d2 = 0 ; if (sign(D1) != sign(d1)) d1 = 0 ; if (sign(D1) != sign(d2)) d2 = 0 ; T a3 = d1 + d2 - 2 * D1; T a2 = 3 * D1 - 2 * d1 - d2; T a1 = d1; T a0 = f1; return a3 * cubic(f) + a2 * square(f) + a1 * f + a0; }
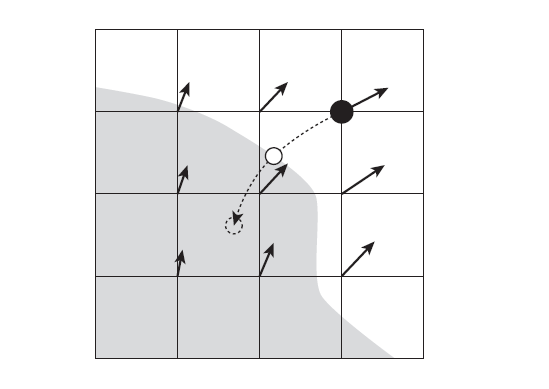
最后，我们还需要考虑后向追踪时的边界处理，我们后向追踪得到的点可能位于碰撞体内部，这个时候就需要做一个截断，使后向追踪的点落到碰撞体的表面上而不是内部，这个过程如下图10所示。我们通过获取网格点的符号距离场与追踪点的符号距离场的符号是否相同来判断是否发生了碰撞体穿透，若发生了穿透也通过它们的符号距离场来获取表面上的点。
图10 截断处理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 Vector3D SemiLagrangian3::backTrace( const VectorField3& flow, double dt, double h, const Vector3D& startPt, const ScalarField3& boundarySdf) { double remainingT = dt; Vector3D pt0 = startPt; Vector3D pt1 = startPt; while (remainingT > kEpsilonD) { Vector3D vel0 = flow.sample(pt0); double numSubSteps = std ::max(std ::ceil (vel0.length() * remainingT / h), 1.0 ); dt = remainingT / numSubSteps; Vector3D midPt = pt0 - 0.5 * dt * vel0; Vector3D midVel = flow.sample(midPt); pt1 = pt0 - dt * midVel; double phi0 = boundarySdf.sample(pt0); double phi1 = boundarySdf.sample(pt1); if (phi0 * phi1 < 0.0 ) { double w = std ::fabs (phi1) / (std ::fabs (phi0) + std ::fabs (phi1)); pt1 = w * pt0 + (1.0 - w) * pt1; break ; } remainingT -= dt; pt0 = pt1; } return pt1; }
上面的代码实现实际上是一个循环，这也是为了提升追踪的精度，每一次后向追踪步长最好不要超过一个$\Delta x$的大小，超过了$\Delta x$我们就把这个追踪过程分成几步，每一步最多走$\Delta x$。半拉格朗日对流的算法复杂度$O(n)$，可以很容易地实现并行版本。
六、流体粘度项 在经过拉格朗日对流之后，我们就需要求解流体的粘度项，流体的粘度项也是流体模拟一个重要的内容。要实现好的流体粘性对于一些高粘度的流体来说至关重要，这是一个研究热点。根据流体力学方程，流体的粘度项为：
其中$a_v$就是在流体的粘性力作用下的加速度，$\mu$粘度系数，$u$流体速度场矢量。求解这一项最简单的方法就是采用一个显式的欧拉前向时间积分：
其中，$\Delta t$为时间步长，$u^n$是当前的速度场，$u^{n+1}$是加入了粘度作用力的速度场，简单的欧拉前向时间积分实现很简单。对于除了流体速度场中的其他物理量场，只需简单地替换公式$(24)$中的速度场矢量即可，下面的代码以标量场为例，我们仅对在流体区域内的网格点做粘度项计算。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 void GridForwardEulerDiffusionSolver3::solve( const ScalarGrid3& source, double diffusionCoefficient, double timeIntervalInSeconds, ScalarGrid3* dest, const ScalarField3& boundarySdf, const ScalarField3& fluidSdf) { auto src = source.constDataAccessor(); Vector3D h = source.gridSpacing(); auto pos = source.dataPosition(); buildMarkers(source.resolution(), pos, boundarySdf, fluidSdf); source.parallelForEachDataPointIndex( [&](size_t i, size_t j, size_t k) { if (_markers(i, j, k) == kFluid) { (*dest)(i, j, k) = source(i, j, k) + diffusionCoefficient * timeIntervalInSeconds * laplacian(src, _markers, h, i, j, k); } else (*dest)(i, j, k) = source(i, j, k); }); }
似乎看起来直接采用前向欧拉法计算流体粘度项非常简单、快速，但与采用基于有限差分法的对流类似，当模拟的时间步长超过一定的阈值时，也会出现不稳定的问题。以1D的情况为例，假设我们要求解物理量场$q$的粘度项，根据中心差分法来估算拉普拉斯算子，有：
在整个求解过程中，$\mu$、$\Delta t$和$\Delta x$时保持不变的，我们把它提取出来并记为$c$，公式$(25)$转变为：
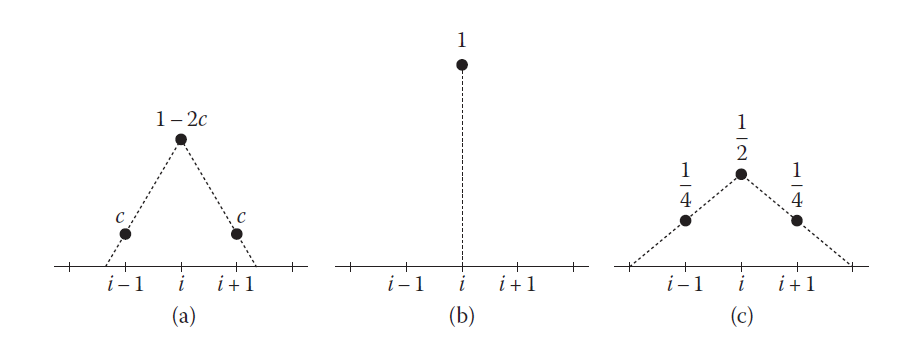
可以看到，把前向欧拉法求解流体粘度项写成公式$(26)$的形式，它就看起来像是一个滤波过程（如下图11(a)所示），对周围的领域做一个加权和，这个权重由$c$决定，因而$c$就是滤波核宽度。$c$越大，则滤波范围越广，从图像处理来说就会导致图像越模糊，在流体模拟这里就会导致流体粘性越大。但是这里的$c$是有范围限制的，$c$的下界为$0$（如下图11(b)所示），这个时候表现为不做任何改变；$c$的上界为$\frac14$（如下图11(c)所示）。超出上界的$c$将会引入中心差分法涉及到的邻域网格点之外的其他网格点，这一点跟前面讨论的逆风对流的缺陷类似。
图11 diffusion filters
因为$c=\frac{\mu \Delta t}{(\Delta x)^2}$，所以$c$的范围限制作用到了流体的粘度系数$\mu$上，假设保持$\Delta t$和$\Delta x$不变，根据$c\leq\frac14$，那么$\mu\leq\frac{(\Delta x)^2}{4\Delta t}$，这意味着我们不能取超过这个范围的流体粘度系数，否则将导致出现不稳定的问题，因此不能实现高粘性的流体（如蜂蜜、油类液体）。事实上，这类不稳定的因素是前向欧拉法固有存在的问题，因此为了实现高粘性的流体，前向欧拉法不能采用。
所以我们将采用的是后向欧拉法，前向欧拉法根据当前的状态以时间推进的顺序计算下一个时间点的状态，而后向欧拉法相反，它假设下一时间点的状态已知，那么可以推算前一个时间点的状态，然后建立一个方程组。后向欧拉法的方程如下（以1D为例）：
公式$(27)$中，我们假设已知下一个时间点的$q_i^{n+1}$，然后推算前一个时间点的$q_i^n$，这个过程是前向欧拉法的逆过程，因而被称为后向欧拉法。这种方法从前往后推算，是无条件稳定的。同样采用中心差分法计算拉普拉斯算子，有：
做一些调整可得方程：
对于每一个$q_i^{n+1}$都可以构建一个上述方程，从而构建了一个大规模的线性方程组。其中$q_i^{n+1}$的系数中的$c$的系数等于其周围4-邻居的数量，例如1D时最左边和最右边其邻居数只有一个，因而其系数为$(c+1)$。二维网格大多数邻居为4，因而其系数为$(4c+1)$，三维依次类推。将线性方程组写成矩阵的形式如下：
公式$(30)$中的系数矩阵是一个大规模的对称稀疏矩阵，问题转成了求解线性方程组$Ax=b$。求解大规模正定稀疏矩阵我们将采用预处理的共轭梯度法，涉及到的数学内容较多，这就不再细细展开。在求解之前需要构建一个稀疏矩阵，这里我们可以不需要耗费大量的空间去存贮大多数的零，其实在这个特定问题下矩阵的每一行元素数量是固定的，1D有3个，2D有5个，3D有7个，又因矩阵是对称的，所以我们每一行只需存储原来的一半。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 void GridBackwardEulerDiffusionSolver3::buildMatrix(const Size3& size, const Vector3D& c) { _system.A.resize(size); bool isDirichlet = (_boundaryType == Dirichlet); _system.A.parallelForEachIndex( [&](size_t i, size_t j, size_t k) { auto & row = _system.A(i, j, k); row.center = 1.0 ; row.right = row.up = row.front = 0.0 ; if (_markers(i, j, k) == kFluid) { if (i + 1 < size.x) { if ((isDirichlet && _markers(i + 1 , j, k) != kAir) || _markers(i + 1 , j, k) == kFluid) row.center += c.x; if (_markers(i + 1 , j, k) == kFluid) row.right -= c.x; } if (i > 0 && ((isDirichlet && _markers(i - 1 , j, k) != kAir) || _markers(i - 1 , j, k) == kFluid)) row.center += c.x; if (j + 1 < size.y) { if ((isDirichlet && _markers(i, j + 1 , k) != kAir) || _markers(i, j + 1 , k) == kFluid) row.center += c.y; if (_markers(i, j + 1 , k) == kFluid) row.up -= c.y; } if (j > 0 && ((isDirichlet && _markers(i, j - 1 , k) != kAir) || _markers(i, j - 1 , k) == kFluid)) row.center += c.y; if (k + 1 < size.z) { if ((isDirichlet && _markers(i, j, k + 1 ) != kAir) || _markers(i, j, k + 1 ) == kFluid) row.center += c.z; if (_markers(i, j, k + 1 ) == kFluid) row.front -= c.z; } if (k > 0 && ((isDirichlet && _markers(i, j, k - 1 ) != kAir) || _markers(i, j, k - 1 ) == kFluid)) row.center += c.z; } }); } void GridBackwardEulerDiffusionSolver3::buildVectors(const ConstArrayAccessor3<double >& f, const Vector3D& c) { Size3 size = f.size(); _system.x.resize(size, 0.0 ); _system.b.resize(size, 0.0 ); _system.x.parallelForEachIndex( [&](size_t i, size_t j, size_t k) { _system.b(i, j, k) = _system.x(i, j, k) = f(i, j, k); if (_boundaryType == Dirichlet && _markers(i, j, k) == kFluid) { if (i + 1 < size.x && _markers(i + 1 , j, k) == kBoundary) _system.b(i, j, k) += c.x * f(i + 1 , j, k); if (i > 0 && _markers(i - 1 , j, k) == kBoundary) _system.b(i, j, k) += c.x * f(i - 1 , j, k); if (j + 1 < size.y && _markers(i, j + 1 , k) == kBoundary) _system.b(i, j, k) += c.y * f(i, j + 1 , k); if (j > 0 && _markers(i, j - 1 , k) == kBoundary) _system.b(i, j, k) += c.y * f(i, j - 1 , k); if (k + 1 < size.z && _markers(i, j, k + 1 ) == kBoundary) _system.b(i, j, k) += c.z * f(i, j, k + 1 ); if (k > 0 && _markers(i, j, k - 1 ) == kBoundary) _system.b(i, j, k) += c.z * f(i, j, k - 1 ); } }); }
构建完了矩阵就可以调用共轭梯度算法求解方程组：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 void GridBackwardEulerDiffusionSolver3::solve( const ScalarGrid3& source, double diffusionCoefficient, double timeIntervalInSeconds, ScalarGrid3* dest, const ScalarField3& boundarySdf, const ScalarField3& fluidSdf) { auto pos = source.dataPosition(); Vector3D h = source.gridSpacing(); Vector3D c = timeIntervalInSeconds * diffusionCoefficient / (h * h); buildMarkers(source.dataSize(), pos, boundarySdf, fluidSdf); buildMatrix(source.dataSize(), c); buildVectors(source.constDataAccessor(), c); if (_systemSolver != nullptr ) { _systemSolver->solve(&_system); source.parallelForEachDataPointIndex( [&](size_t i, size_t j, size_t k) { (*dest)(i, j, k) = _system.x(i, j, k); }); } }
七、流体压强梯度项 流体的压强项同样是采用了后向欧拉法，这样才能够保证流体模拟的无条件稳定。根据Navier-Stokes方程，流体的压强梯度项为：
其中的$a_p$是流体内部压强梯度力作用下的加速度。采用后向欧拉的思想，我们已知下一个时间点的速度场$u^{n+1}$，求解压强梯度项就是为了保证流体的不可压缩性，即散度为零：
设流体的密度保持不变，从而可得：
上面推导处的方程与流体的粘度方程类似，左边是关于压强的拉普拉斯项，为未知项目，右边是关于当前速度场的散度，为已知项。这个就是关于压强的泊松方程（Pressure Poisson equation，简称为PPE），同样采用中心差分法计算拉普拉斯算子和散度：
与求解粘度方程类似，将其写成大规模稀疏的对称正定矩阵：
同样地采用共轭梯度法求解上述的大规模的稀疏对称正定线性方程组。
八、烟雾流体模拟 我们要模拟的烟雾是燃烧或者爆炸产生的，通常在烟雾周围的温度高于其他区域，温度较高的空气密度较低，从而产生一个上升力。与此同时，烟雾聚集的区域其质量增大，因而也会受到重力的因素产生下降力。这些垂直方向上的力就是浮力。一种计算浮力的方式就是考虑流体密度的变化，原来的压强泊松方程中的密度场$\rho$不再是常量，而是会发生变化的，故求散度时不能直接提出公式外面，前面的公式$(33)$就变成了$^{[3]}$：
公式$(36)$求解的是精确的浮力，需要耗费大量的计算资源，在一些密度差异非常关键的场合中这是非常重要的。但是在计算机图形学的烟雾模拟中不需要这么高精度地去计算流体密度产生的浮力作用力，我们采用下面的近似计算公式$^{[5]}$：
公式$(37)$中的$\alpha$和$\beta$是缩放系数，用于控制流体密度和温度对浮力的影响，$f_{buoy}$就是流体浮力，$T$是流体的温度场，$T_{amb}$为周围环境的温度，$\rho$密度场，$\vec y$时垂直方向上的单位向量。$T_{amb}$可以通过计算温度场的平均温度得到。公式$(37)$综合考虑了流体密度和流体温度的影响。流体密度的影响是产生一个垂直向下的作用力，因而$\alpha \rho \vec y$前面还有个负号；流体温度的影响取决于当前温度与环境温度的差，高于环境温度会产生一个向上的作用力。
烟雾模拟需要存储的流体属性有速度场、密度场以及温度场，后两个都是标量场。这些属性在流体模拟中，都需要求解整个流体方程，即均需求解体积力项、对流项、粘度项以及压力项。在这里体积力项仅仅有浮力项（即公式$(37)$），重力因素已经被考虑进公式$(37)$了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 void GridSmokeSolver3::computeBuoyancyForce(double timeIntervalInSeconds){ auto grids = gridSystemData(); auto vel = grids->velocity(); Vector3D up (0 , 1 , 0 ) ; if (gravity().lengthSquared() > kEpsilonD) up = -gravity().normalized(); if (std ::abs (_buoyancySmokeDensityFactor) > kEpsilonD || std ::abs (_buoyancyTemperatureFactor) > kEpsilonD) { auto den = smokeDensity(); auto temp = temperature(); double tAmb = 0.0 ; temp->forEachCellIndex([&](size_t i, size_t j, size_t k) { tAmb += (*temp)(i, j, k); }); tAmb /= static_cast <double >(temp->resolution().x * temp->resolution().y * temp->resolution().z); auto u = vel->uAccessor(); auto v = vel->vAccessor(); auto w = vel->wAccessor(); auto uPos = vel->uPosition(); auto vPos = vel->vPosition(); auto wPos = vel->wPosition(); if (std ::abs (up.x) > kEpsilonD) { vel->parallelForEachUIndex([&](size_t i, size_t j, size_t k) { Vector3D pt = uPos(i, j, k); double fBuoy = _buoyancySmokeDensityFactor * den->sample(pt) + _buoyancyTemperatureFactor * (temp->sample(pt) - tAmb); u(i, j, k) += timeIntervalInSeconds * fBuoy * up.x; }); } if (std ::abs (up.y) > kEpsilonD) { vel->parallelForEachVIndex([&](size_t i, size_t j, size_t k) { Vector3D pt = vPos(i, j, k); double fBuoy = _buoyancySmokeDensityFactor * den->sample(pt) + _buoyancyTemperatureFactor * (temp->sample(pt) - tAmb); v(i, j, k) += timeIntervalInSeconds * fBuoy * up.y; }); } if (std ::abs (up.z) > kEpsilonD) { vel->parallelForEachWIndex([&](size_t i, size_t j, size_t k) { Vector3D pt = wPos(i, j, k); double fBuoy = _buoyancySmokeDensityFactor * den->sample(pt) + _buoyancyTemperatureFactor * (temp->sample(pt) - tAmb); w(i, j, k) += timeIntervalInSeconds * fBuoy * up.z; }); } applyBoundaryCondition(); } }
然后就是流体密度和流体温度的对流以及粘性计算，对流没什么需要特殊处理，这里不再赘述。粘性扩散计算其实也没什么特殊的地方，我们直接调用前面的流体粘性解算器。在求解完流体密度和温度的粘性项之后，我们给流体的密度和温度做一个衰减：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 void GridSmokeSolver3::computeDiffusion(double timeIntervalInSeconds) { if (diffusionSolver() != nullptr ) { if (_smokeDiffusionCoefficient > kEpsilonD) { auto den = smokeDensity(); auto den0 = std ::dynamic_pointer_cast<CellCenteredScalarGrid3>(den->clone()); diffusionSolver()->solve(*den0, _smokeDiffusionCoefficient, timeIntervalInSeconds, den.get(), *colliderSdf()); extrapolateIntoCollider(den.get()); } if (_temperatureDiffusionCoefficient > kEpsilonD) { auto temp = smokeDensity(); auto temp0 = std ::dynamic_pointer_cast<CellCenteredScalarGrid3>(temp->clone()); diffusionSolver()->solve(*temp0, _temperatureDiffusionCoefficient, timeIntervalInSeconds, temp.get(), *colliderSdf()); extrapolateIntoCollider(temp.get()); } } auto den = smokeDensity(); den->parallelForEachDataPointIndex([&](size_t i, size_t j, size_t k) { (*den)(i, j, k) *= 1.0 - _smokeDecayFactor; }); auto temp = temperature(); temp->parallelForEachDataPointIndex([&](size_t i, size_t j, size_t k) { (*temp)(i, j, k) *= 1.0 - _temperatureDecayFactor; }); }
整个工程的代码具体见这里 。
参考资料： $[1]$ Stam J. Stable fluids[J]. Acm Transactions on Graphics, 1999, 1999:121—128.
$[2]$ A. J. Chorin and J. E. Marsden. A Mathematical Introduction to Fluid Mechanics. Springer-Verlag. Texts in Applied Mathematics 4. Second Edition., New York, 1990.
$[3]$ Kim, D. (2017). Fluid engine development . Boca Raton: Taylor & Francis, a CRC Press, Taylor & Francis Group.
$[4]$ R. Bridson and M. Müller-Fischer. Fluid simulation: Siggraph 2007 course notes. In ACM SIGGRAPH 2007 Courses, pages 1–81, ACM, 2007.
$[5]$ Fedkiw R, Stam J, Jensen H W. Visual simulation of smoke[C]// Conference on Computer Graphics & Interactive Techniques. 2001.
