流体模拟Fluid Simulation：求解流体不可压缩的泊松方程

WC Yang

2019-08-03

Computer Graphics / Fluid Simulation

本文主要是流体不可压缩投影，在进行半拉格朗日对流之后，还需要对流体速度进行修正，使流体的速度场散度为零。主要是关于流体压强的泊松方程求解，通常采用共轭梯度法求解大规模稀疏矩阵的线性方程组，辅以不完全的Cholesky因子化。涉及到的数学内容比较多。

离散的压力梯度
离散的速度场散度
求解关于压强的泊松方程
不可压缩投影
参考资料

流体的不可压缩投影

在流体模拟中，确保流体的不可压缩性是非常重要、关键的一步，也是最耗时的一步，这是整个流体模拟过程中的核心，涉及到模拟效果的真实性、模拟过程的效率快慢两方面的内容，因而相关的数学内容比较多。在流体模拟中，确保流体的不可压缩性的算法我们通常用$project(\Delta t, \vec u)$来表示，它输入时间步长$\Delta t$和流体的速度场$\vec u$，然后在流体内部的压力的作用下更新速度场：

$\vec u^{n+1}=\vec u-\Delta t\frac1\rho \nabla p \tag {1}$

上述公式中，$\vec u^{n+1}$就是新的速度场，$\rho$是流体密度，$p$为压力。通过公式$(1)$，我们就可以得到满足流体不可压缩性的流体，此时得到的新速度场$\vec u^{n+1}$的散度为0：

$\nabla \cdot \vec u^{n+1}=0 \tag {2}$

且在固体边界处，其速度场在法线方向上的投影等于固定墙的速度场在法线方向上的投影：

$\vec u^{n+1}\cdot \vec n=\vec u_{solid}\cdot \vec n \tag {3}$

在前一步展开如何求解上述的几个公式之前，我们先把流体模拟区域划分成一个一个格子，有流体的格子标记为F，固体边界区域的格子标记为$S$，空白的区域则标记为$E$。下图1展示了一个二维的例子。

图1 模拟区域标记

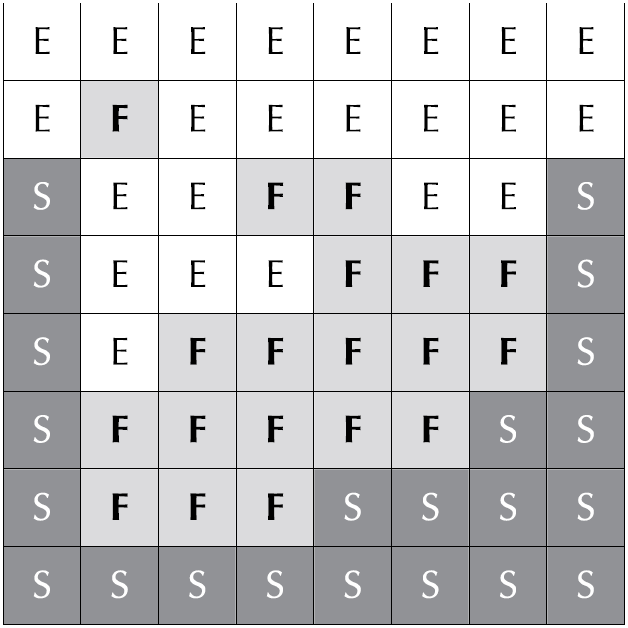
模拟的网格依旧是MAC网格，即交错的网格结构，如下图2所示。格子中心存储流体压力值，边缘部分存储流体的速度场向量，依次交错存储。

图2 MAC网格

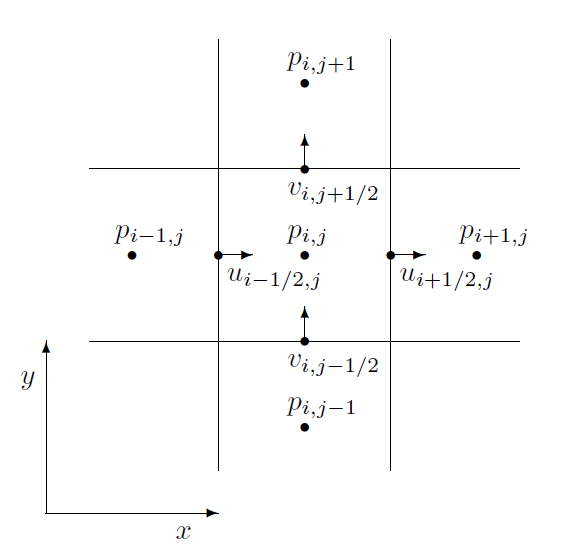
一、离散的压力梯度

MAC网格解决了普通的网格的零域（null space）问题，在使用中心差分法计算梯度时鲁棒性更强。目前暂时假设流体的压力值已经知道且存储在MAC网格上，那么二维和三维的压力梯度计算采用中心差分法如下所示：

$\nabla p=(\frac{p_{i+1,j}-p_{i,j}}{\Delta x},\frac{p_{i,j+1}-p_{i,j}}{\Delta x})\\ \nabla p=(\frac{p_{i+1,j,k}-p_{i,j,k}}{\Delta x}, \frac{p_{i,j+1,k}-p_{i,j,k}}{\Delta x}, \frac{p_{i,j,k+1}-p_{i,j,k}}{\Delta x}) \tag {4}$

然后将公式$(4)$中的离散压力梯度公式代入公式$(1)$，可以得到实际上的速度场更新公式：

$\begin{cases} u_{i+1/2,j}^{n+1}=u_{i+1/2,j}-\Delta t\frac1\rho\frac{p_{i+1,j}-p_{i,j}}{\Delta x}\\ v_{i,j+1/2}^{n+1}=v_{i,j+1/2}-\Delta t\frac1\rho\frac{p_{i,j+1}-p_{i,j}}{\Delta x} \end{cases}\\ \begin{cases} u_{i+1/2,j,k}^{n+1}=u_{i+1/2,j,k}-\Delta t\frac1\rho\frac{p_{i+1,j,k}-p_{i,j,k}}{\Delta x}\\ v_{i,j+1/2,k}^{n+1}=v_{i,j+1/2,k}-\Delta t\frac1\rho\frac{p_{i,j+1/2,k}-p_{i,j,k}}{\Delta x}\\ w_{i,j,k+1/2}^{n+1}=w_{i,j,k+1/2}-\Delta t\frac1\rho\frac{p_{i,j,k+1/2}-p_{i,j,k}}{\Delta x} \end{cases} \tag {5}$

公式$(5)$给出了二维和三维的流体不可压缩速度场更新公式。注意，固体墙边界并没有压力一说，而自由面边界压力我们设置为零，这样上述的公式仅适用于那些不邻近固体边界的速度场分量，一般情况下至少需要邻近一个流体区域。

现在我们把目标放到边界条件的处理上。首先是自由面，这部分通常就是空气，我们直接设置其压力值为零，这类边界处理我们称之为第一类边界条件——狄利克雷边界条件（Dirichlet boundary condition）$^{[1]}$。所谓狄利克雷边界条件，就是我们直接设定边界处的值，这是在数值方法中最简单的一种边界处理方法。

然后就是固体墙边界的处理。在固体墙边界部分，我们需要将流体的速度场在法线方向上的投影等于固体边界在法相方向上的速度场向量值，一种方法就是直接设置，例如在$(i+1/2,j,k)$处的速度场分量$u$，假设其左边$(i,j,k)$为固体边界区域，右边$(i+1,j,k)$为流体区域，那么直接赋值$u$：

$u_{i+1/2,j,k}^{n+1}=u_{i+1/2,j,k}^{solid} \tag {6}$

直接赋值需要一个额外的分支进行。另外一种方案就是给固定墙区域设定一个ghost压强值，只要通过公式$(5)$更新后固体边界处的速度场为公式$(6)$即可，此时不需要额外的分支。通过一些变换，可得固体墙区域的ghost压强计算公式：

$p_{i,j,k}^{ghost}=p_{i+1,j,k}-\frac{\rho\Delta x}{\Delta t}(u_{i+1/2,j,k}-u_{i+1/2,j,k}^{solid}) \tag {7}$

这种方案在进行不可压缩投影时不需要考虑邻域是否是固体边界，统一用公式$(5)$计算，在固体边界处用ghost压强值计算，依旧以上面为例：

$u_{i+1/2,j,k}^{n+1}=u_{i+1/2,j,k}-\Delta t\frac{1}{\rho}\frac{p_{i+1,j,k}-p_{i,j,k}^{ghost}}{\Delta x} \tag {8}$

实际上，将公式$(7)$代入公式$(8)$中，就可以得到公式$(6)$，通过这种方式不再将固体边界的处理作为一个单独考虑的情况。将公式$(8$做一些移项，重写为：

$\frac{\Delta t}{\rho}\frac{p_{i+1,j,k}-p_{i,j,k}^{ghost}}{\Delta x}= u_{i+1/2,j,k}-u_{i+1/2,j,k}^{solid} \tag {9}$

上述公式中的左边压强部分可以看成是关于压强梯度的有限差分，即关于下面公式的一个近似：

$\frac{\Delta t}{\rho}\frac{\partial p}{\partial x}=u-u^{solid} \tag {10}$

公式$Math Processing Error$仅仅是关于一个方向，同样地，我们可以取其他方向的固体边界条件，得到更一般的公式：

$\frac{\Delta t}{\rho}\nabla p\cdot \vec n=(\vec u-\vec u^{solid})\cdot \vec n \tag {11}$

公式$(11)$给出了固体边界处的压力梯度值，与狄利克雷条件处理方式不同，这里给出的是梯度的取值，这种边界处理方式被称为第二类边界条件——冯诺依曼边界条件（Neumannn boundary condition）$^{[1]}$。最后，假设流体的压力已知（实际上未知），根据压力梯度更新流体的速度场，算法伪代码如下：

scale = dt/(density*dx);
loop over i,j,k:
	#update u component.
	if label(i-1,j,k)==FLUID or label(i,j,k)==FLUID:
		if label(i-1,j,k)==SOLID or label(i,j,k)==SOLID:
			u(i,j,k) = usolid(i,j,k);
		else
			u(i,j,k) -= scale * (p(i,j,k) - p(i-1,j,k));
	else
		mark u(i,j,k) as unknown;
	#update v component.
    if label(i,j-1,k)==FLUID or label(i,j,k)==FLUID:
        if label(i,j-1,k)==SOLID or label(i,j,k)==SOLID:
        	v(i,j,k) = vsolid(i,j,k);
        else
        	v(i,j,k) -= scale * (p(i,j,k) - p(i,j-1,k));
    else
    	mark v(i,j,k) as unknown;
	#update w component.
    if label(i,j,k-1)==FLUID or label(i,j,k)==FLUID:
        if label(i,j,k-1)==SOLID or label(i,j,k)==SOLID:
        	w(i,j,k) = wsolid(i,j,k);
        else
        	w(i,j,k) -= scale * (p(i,j,k) - p(i,j,k-1));
    else
    	mark w(i,j,k) as unknown;

二、离散的速度场散度

流体不可压缩的最终表现就是速度场的散度为零，即$\nabla \cdot \vec u=0$。经过不可压缩投影之后新的速度场$\vec u^{n+1}$应该满足散度为零的条件，我们通过有限差分法估算新速度场$\vec u^{n+1}$的散度。首先是散度的数学定义，二维和三维的散度定义如下所示：

$\nabla \cdot \vec u=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\\ \nabla \cdot \vec u=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+ \frac{\partial w}{\partial z} \tag {12}$

给定一个二维欧拉网格$(i,j)$，采用中心差分法计算离散的散度公式如下：

$(\nabla\cdot \vec u)_{i,j}\approx \frac{u_{i+1/2,j}-u_{i-1/2,j}}{\Delta x}+\frac{v_{i,j+1/2}-v_{i,j-1/2}}{\Delta x} \tag {13}$

同理，三维$(i,j,k)$的离散散度计算公式为：

$(\nabla\cdot \vec u)_{i,j,k}\approx \frac{u_{i+1/2,j,k}-u_{i-1/2,j,k}}{\Delta x} +\frac{v_{i,j+1/2,k}-v_{i,j-1/2,k}}{\Delta x} +\frac{w_{i,j,k+1/2}-w_{i,j,k-1/2}}{\Delta x} \tag {14}$

事实上，我们更关心散度的相反数，且仅对于流体区域计算其散度值，其余的固体边界、自由面部分不需要计算散度值。下面是一个计算流体散度的伪代码。

scale = 1/dx;
loop over i,j,k where label (i,j,k)==FLUID:
	rhs(i,j,k)=-scale * (u(i+1,j,k)-u(i,j,k)
                        +v(i,j+1,k)-v(i,j,k)
                        +w(i,j,k+1)-w(i,j,k));

给定一个流体区域及其表面$\partial cell$，流体散度的意义就是流体流进流出的总比例：

$\int\int_{\partial cell}\vec u \cdot \vec n \tag {15}$

若流体区域为一个欧拉网格的立方体格子，那么上述的积分就是对立方体六个面上的速度场进行积分。这种方法与我们前面讨论的有限差分法不同，这是有限体积法（Finite volume method）。这里只是顺带一提。

三、求解关于压强的泊松方程

在前面我们讨论了如何在已知流体内部压强的情况下进行不可压缩投影，更新速度场，并估算速度场的散度值。实际上，流体内部压强并不知道，这需要我们计算得到。接下来的内容就是关于如何求解流体的压力数值，这部分涉及的数学内容比较多，是比较难的一部分。

1、泊松方程

我们知道新的速度场$\vec u^{n+1}$需要满足散度为零，从而保证流体的不可压缩条件。又已知新的速度场$\vec u^{n+1}$计算公式为上面的公式$(5)$，离散的散度计算公式为公式$(13)$和公式$(14)$，我们将公式$(5)$得到的速度场代入公式$(13)$、$(14)$中，就可以得到以流体压力为未知量的线性方程。

我们先来看二维的情况，关于$\vec u^{n+1}$的散度为零表示成如下：

$\frac{u_{i+1/2,j}^{n+1}-u_{i-1/2,j}^{n+1}}{\Delta x} + \frac{v_{i,j+1/2}^{n+1}-v_{i,j-1/2}^{n+1}}{\Delta x} = 0 \tag {16}$

将公式$(5)$中二维的速度更新公式代入上面的公式$(16)$中，可得：

$\frac{1}{\Delta x}[(u_{i+1/2,j}-\Delta t\frac1\rho\frac{p_{i+1,j}-p_{i,j}}{\Delta x}) -(u_{i-1/2,j}-\Delta t\frac1\rho\frac{p_{i,j}-p_{i-1,j}}{\Delta x})\\ +(v_{i,j+1/2}-\Delta t\frac1\rho\frac{p_{i,j+1}-p_{i,j}}{\Delta x}) -(v_{i,j-1/2}-\Delta t\frac1\rho\frac{p_{i,j}-p_{i,j-1}}{\Delta x})]=0\\ \to \\ \frac{\Delta t}{\rho}(\frac{4p_{i,j}-p_{i+1,j}-p_{i,j+1}-p_{i-1,j}-p_{i,j-1}}{\Delta x^2}) =-(\frac{u_{i+1/2,j}-u_{i-1/2,j}}{\Delta x}+\frac{v_{i,j+1/2}-v_{i,j-1/2}}{\Delta x}) \tag {17}$

三维的情况同理，只不过多了一维需要处理：

$\frac{u_{i+1/2,j,k}^{n+1}-u_{i-1/2,j,k}^{n+1}}{\Delta x} + \frac{v_{i,j+1/2,k}^{n+1}-v_{i,j-1/2,k}^{n+1}}{\Delta x} + \frac{w_{i,j,k+1/2}^{n+1}-w_{i,j,k-1/2}^{n+1}}{\Delta x} = 0 \tag {18}$ $\frac{1}{\Delta x}[(u_{i+1/2,j,k} -\Delta t\frac1\rho\frac{p_{i+1,j,k}-p_{i,j,k}}{\Delta x}) -(u_{i-1/2,j,k}-\Delta t\frac1\rho\frac{p_{i,j,k}-p_{i-1,j,k}}{\Delta x})\\ +(v_{i,j+1/2,k}-\Delta t\frac1\rho\frac{p_{i,j+1,k}-p_{i,j,k}}{\Delta x}) -(v_{i,j-1/2,k}-\Delta t\frac1\rho\frac{p_{i,j,k}-p_{i,j-1,k}}{\Delta x})]\\ +(w_{i,j,k+1/2}-\Delta t\frac1\rho\frac{p_{i,j,k+1}-p_{i,j,k}}{\Delta x}) -(w_{i,j,k-1/2}-\Delta t\frac1\rho\frac{p_{i,j,k}-p_{i,j,k-1}}{\Delta x})]=0\\ \to \\ \frac{\Delta t}{\rho}(\frac{6p_{i,j,k}-p_{i+1,j,k}-p_{i,j+1,k}-p_{i,j,k+1}-p_{i-1,j,k}-p_{i,j-1,k}-p_{i,j,k-1}}{\Delta x^2}) \\ = -( \frac{u_{i+1/2,j,k}-u_{i-1/2,j,k}}{\Delta x} + \frac{v_{i,j+1/2,k}-v_{i,j-1/2,k}}{\Delta x} + \frac{w_{i,j,k+1/2}-w_{i,j,k-1/2}}{\Delta x} ) \tag {19}$

仔细观察上面的公式$(17)$和公式$(19)$，可以发现他们都是泊松问题$-\Delta t/\rho \nabla \cdot \nabla p=-\Delta \cdot \vec u$的一个离散计算公式，左边是关于压力的拉普拉斯算子的数值近似，右边是关于速度场散度的数值近似，我们最终要求解的就是这么一个关于压力的方程。方程右边是散度的相反数，这就是我们前面计算并保存的是散度的相反数的原因。当邻居格子是自由面边界时，我们直接将其相应的压力值取零；当邻居格子是固体墙边界时，我们根据冯诺依曼边界条件计算得到的压强替换相应的压力项。

2、写成矩阵形式

上面讨论的仅仅是一个格子的压力项求解方程，事实上我们要求解的是整个流体区域的压力项值。为此，为了便于阐述和求解，我们将上面的线性方程写成矩阵乘向量的形式。我们将方程中所有压力项的系数提出来，写成一个系数矩阵$A$，所有流体区域的压力项写成一个未知变量的向量$p$，相应的所有流体区域的负散度作为线性方程组右边的向量$b$，那么我们要求解的就是下面的一个大规模非齐次线性方程组：

$Ap=b \tag {20}$

矩阵$A$每一行存储的是一个流体格子求解压力项的系数。仔细观察公式$(17)$和$(19)$，实际上每一行的系数中仅仅只有几个不为0，不为0的系数是其周围邻居和自身的。在三维情况下，给定$(i,j,k)$这个流体格子，那么其对应的矩阵$A$中的那一行中，仅仅是$p_{i,j,k}$、$p_{i\pm 1,j,k}$、$p_{i,j\pm 1,k}$和$p_{i,j,k\pm 1}$对应的系数不为0，即又7个不为的系数，剩下的系数全部为0。二维就是一行有5个系数不为0。可以看到矩阵$A$是一个大规模的稀疏矩阵，大部分的矩阵元素都为0，所以我们没有必要直接存储矩阵$A$，因为这样将会极大地耗费内存，甚至出现内存不足的情况，因为矩阵A实在是太大了。

仔细观察前面公式$(17)$和$(19)$的线性方程，对于给定的流体格子$(i,j,k)$，其邻域压力项的系数为$-\Delta t/(\rho \Delta x^2)$，自身压力项的系数为邻居格子中流体格子或者空气（自由面）格子的数量$n_{i,j,k}$在乘上$\Delta t/(\rho\Delta x^2)$，即$n_{i,j,k}\Delta t/(\rho \Delta x^2)$，可以看到在三维时$n_{i,j,k}$至多为6、在二维时至多为$4$。

同时，系数矩阵$A$也是一个对阵矩阵。举个例子，$A_{(i,j,k)(i+1,j,k)}$是方程组中关于$p_{i+1,j,k}$的系数，那么它必然等于$A_{(i+1,j,k)(i,j,k)}$，这是因为$(i+1,j,k)$是$(i,j,k)$的邻居，那么$(i,j,k)$必然也是$(i+1,j,k)$的邻居。系数矩阵$A$既然是对阵矩阵，那么我们存储系数矩阵$A$时又可以减少一半的存储量了，只需存储上三角形、或者下三角矩阵。

经过上述的讨论，对于大规模的稀疏矩阵$A$，以二维为例，我们采用的存储方案为：每一个流体格子存储关于自身压力项的系数$A_{(i,j)(i,j)}$，这个就是矩阵$A$中的对角线元素，而关于邻居流体格子压力项的系数我们仅存储正向方向上的（因为对称）$A_{(i,j),(i+1,j)}$和$A_{(i,j)(i,j+1)}$。我们记矩阵$A$的对角线元素为Adiag(i,j)，$x$轴方向的矩阵元素Ax(i,j)，$y$轴方向的矩阵元素Ay(i,j)。三维同理，分别存储到Adiag(i,j,k)、Ax(i,j,k)、Ay(i,j,k)、Az(i,j,k)，一个三维的系数矩阵$A$的计算并存储的伪代码如下所示：

scale = dt / (density*dx*dx);
loop over i,j,k:
    if label(i,j,k)==FLUID:
        # handle negative x neighbor
        if label(i-1,j,k)==FLUID:
        	Adiag(i,j,k) += scale;
        # handle positive x neighbor
        if label(i+1,j,k)==FLUID:
        	Adiag(i,j,k) += scale;
        	Ax(i,j,k) = -scale;
        else if label(i+1,j,k)==EMPTY:
        	Adiag(i,j,k) += scale;
        # handle negative y neighbor
        if label(i,j-1,k)==FLUID:
        	Adiag(i,j,k) += scale;
        # handle positive y neighbor
        if label(i,j+1,k)==FLUID:
        	Adiag(i,j,k) += scale;
        	Ay(i,j,k) = -scale;
        else if label(i,j+1,k)==EMPTY:
        	Adiag(i,j,k) += scale;
        # handle negative z neighbor
        if label(i,j,k-1)==FLUID:
        	Adiag(i,j,k) += scale;
        # handle positive z neighbor
        if label(i,j,k+1)==FLUID:
        	Adiag(i,j,k) += scale;
        	Az(i,j,k) = -scale;
        else if label(i,j,k+1)==EMPTY:
        	Adiag(i,j,k) += scale;

3、共轭梯度算法

现在我们把目标放到求解大规模的非齐次线性方程组上，即上面的公式$(20)$。系数矩阵$A$除了是一个大规模的稀疏对称矩阵之外，还是一个正定（Positive definite）矩阵，即对于任意的非零向量$q$，$q^TAq>0$均成立，且系数矩阵$A$的所有特征值均大于0。当然在实际情况下，系数矩阵$A$可能不是一个严格的正定矩阵，而是一个半正定矩阵，即对于任意非零向量$q$，有$q^TAq\geq0$。这种情况出现在流体模拟区域中，存在一些流体区域完全被固体墙边界包围，此时的系数矩阵$A$不是一个严格的正定矩阵，甚至此时的矩阵$A$是一个奇异矩阵，它不存在逆矩阵，从而导致方程$(20)$不一定有解。因而在一些特殊情况下，我们求解的是兼容条件下的解，即只要使得流体-固体边界处流体的流进和流出保持平衡（流进量等于流出量）即可。

求解一个线性方程组最常用、最暴力的方法就是高斯消元法，逐行进行消元，最后使得矩阵变成一个上三角矩阵，从最后一行往回代即可求解出方程的解（只要解存在）。但是高斯消元法实在是太慢了，小规模的矩阵来说还好，大规模的矩阵方程求解一般不会这么直接暴力解。这里我们采用的求解方程$(20)$的方法是共轭梯度算法（Conjugate gradient method，简称为CG）$^{[2]}$。相比于普通的高斯消元法，共轭梯度算法采用了一个迭代的流程，迭代到给定的收敛程度即可，整个算法流程只涉及到矩阵-向量乘法、向量加减、向量-标量乘法以及非常少的点乘操作，这些都可以快速并行地计算。

共轭梯度算法就是针对对称正定矩阵的线性方程组的求解，给定一个线性方程组如下$(21)$所示，其中系数矩阵$A$是一个元素均已知的实对称正定矩阵，右边的向量$\vec b$也已知，我们要求解的就是未知向量$\vec x$。这个就是共轭梯度所要解决的线性方程组。

$A x= b \tag {21}$

给定两个非零向量$u$和$v$，我们说它们是共轭的（相对于$A$），若：

$u^TAv = 0 \tag {22}$

而矩阵$A$是一个对称的正定矩阵（故有$A^T=A$），那么上式的左边可以写成多种向量内积的形式，它们完全是等价的。这样两个非零向量是共轭的，当且仅当这两个向量相对于下面的内积是正交的。共轭是一个对称的相互关系，$u$共轭于$v$，那么$v$也共轭于$u$。

$u^TAv=<u,v>_A=<Au,v>=<u,A^Tv>=<u,Av> \tag {23}$

令$P=\{p_1,…,p_n\}$是一个这样的向量集合，集合中的所有向量都相对于$A$互相共轭，那么$P$构成了$R^n$空间的一个基，方程$(21)$的解$x_*$可以用这组基的线性组合来表示：

$x_*=\Sigma_{i=1}^n\alpha_i p_i \tag {24}$

将上述的$x_*$表达式代入方程$(21)$中，有：

$Ax_*=\Sigma_{i=1}^n\alpha_iAp_i \tag {25}$

再左乘上$P$中的一个向量$p_k^T$：

$p_k^TAx_*=\Sigma_{i=1}^n\alpha_ip_k^TAp_i \tag {26}$

然后将$Ax_*=b$、$u^TAv=(u,v)_A$代入公式$(26)$中：

$p_k^Tb=\Sigma_{i=1}^n\alpha_i <p_k,p_i>_A \tag {27}$

最后根据$u^Tv=(u,v)$以及$\forall i\neq k: (p_k,p_i)_A=0$，可得：

$<p_k,b>=\alpha_k <p_k,p_k>_A \\ \to \\ \alpha_k=\frac{<p_k,b>}{<p_k,p_k>_A} \tag {28}$

由此，我们可以得到一个求解方程$Ax=b$的方法，首先找到$n$个互相共轭的向量，然后计算其组合系数$\alpha_k$，最后未知向量就由这$n$个互相共轭的向量线性组合而成（即公式$(24)$）。但显然直接寻找$n$个互相共轭的向量在$n$比较大的时候不现实，因为这将耗费大量的时间。

共轭梯度采用的是迭代法，我们给出了一个初始预测解$x_0$，致力于寻找最终解$x_d$，通过迭代的方法使得初始的预测解$x_0$逐步向$x_d$逼近，每一次的迭代中我们挑选出一个共轭向量$p$。迭代过程中的目标就是最小化预测向量与最终解$x_d$之间的差距，此时我们的问题就转换为如下的二次方程的最优化问题：

$f(x)=x^T(\frac12Ax-b)=\frac12x^TAx-x^Tb, x\in R^n \tag {29}$

公式$(29)$是一个关于$n$维向量的二次方程，是一个$n$元函数，其一阶导数和二阶导数分别如下所示：

$\nabla f(x)=Ax-b \\ \nabla^2 f(x)=A \tag {30}$

可以看到当二次方程的一阶导数$Ax-b=0$时，此时的$x$就是我们要求的线性方程组的解，此时二次方程取得最小值。共轭梯度法在初次迭代时直接取第一个共轭向量$p_0=b-Ax_0$，即负梯度方向，这一步与梯度下降法类似。但是后续迭代取的向量就不再是负梯度向量了，而是取一个与梯度向量共轭的向量，这就是名称共轭梯度法的由来。实际上，每一次迭代时我们取的负梯度向量就是当前预测解与最终解之间的残差（Residual），第$k$次迭代时的残差为：

$r_k=b-Ax_k \tag {31}$

为了确保在每一次迭代中取得的向量共轭于梯度以及前面迭代得到的向量，我们结合残差向量以及前面迭代的向量计算当前迭代挑选的向量：

$p_k=r_k-\Sigma_{i<k}\frac{p_i^T A r_k}{p_i^TAp_i}p_i \tag {32}$

第$k+1$次迭代时取得的预测解向量计算公式为：

$x_{k+1}=x_k+\alpha_kp_k \tag {33}$

其中$\alpha_k$的计算公式为：

$\alpha_k=\frac{p_k^T(b-Ax_k)}{p_k^TAp_k}=\frac{p_k^Tr_k}{p_k^TAp_k} \tag {34}$

最终，共轭梯度法求解线性方程组的伪代码如下图3所示。

图3 共轭梯度算法

然而，为了进一步加快求解的收敛速度，我们采用的预处理的共轭梯度法（Preconditioned conjugate gradient method，简称为PCG）$^{[2]}$，该算法预先定义了一个特殊的矩阵$M$，具体的算法流程如下图4所示。

图4 预处理共轭梯度算法

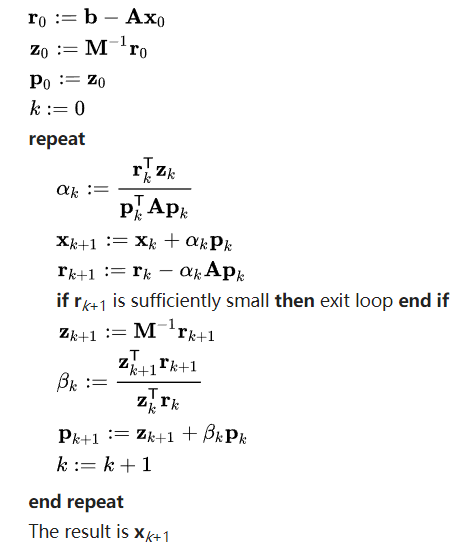
预处理共轭梯度法等价于共轭梯度法计算如下线性方程组的解：

$E^{-1}A(E^{-1})^TE^Tx=E^{-1}b \tag {35}$

其中，预处理共轭梯度法里面的矩阵$M=EE^T$，$M$也是一个保持不变的对称正定矩阵（上面的内容来自维基百科，我感觉这里是的矩阵$M$就是矩阵$A$）。目前已经有多种预处理方法，Robert Brdision在书中介绍了一种预处理方法，该预处理方法被称为不完全的Cholesky因子化（Incomplete Cholesky factorization）$^{[3]}$。

Cholesky因子化是这样的一个数学含义：给定一个正定矩阵$A$，可以找到一个这样的下三角矩阵$L$，使得$A=LL^T$。不完全Chkolesky因子化就是寻找一个近似于$L$的矩阵$K$，使得$A=LL^T\approx KK^T$。这里之所以不寻找确切的下三角矩阵$L$，是因为即便$A$是一个包含大量0元素的稀疏矩阵，但是其因子化的下三角矩阵$L$却不一定是稀疏矩阵，大规模的非稀疏矩阵将带来非常严重的内存问题。因此，我们希望寻找这样的一个因子化矩阵$K$，矩阵$A$中为0的元素，在矩阵$K$相应的地方亦为0，构成类似的一个稀疏矩阵。这就是不完全的Cholesky因子化。

上面讨论的不完全Cholesky因子化只允许矩阵$k$非零元素与矩阵$A$的非零元素具有一样的分布，这就是0级的不完全Cholesky因子化，通常记为IC(0)。首先我们将矩阵$A$分成一个下三角矩阵$F$和对角矩阵$D$：

$A=F+D+F^T \tag {36}$

然后IC(0)的因子化矩阵$K$有如下的形式：

$K=FE^{-1}+E \tag {37}$

其中矩阵$E$是一个对角矩阵，因此对于因子化矩阵$K$，只有对角矩阵$E$未知，剩下的矩阵$F$可以直接从矩阵$A$中获取。Robert Brdison直接给出了计算对角矩阵$E$的计算公式，二维和三维的计算公式如下所示：

$E_{(i,j)}=\sqrt{A_{(i,j),(i,j)}-(A_{(i-1,j),(i,j)}/E_{(i-1,j)})^2-(A_{(i,j-1),(i,j)}/E_{(i,j-1)})^2}\\ E_{(i,j,k)}=\sqrt{A_{(i,j,k),(i,j,k)}-(A_{(i-1,j,k),(i,j,k)}/E_{(i-1,j,k)})^2 -(A_{(i,j-1,k),(i,j,k)}/E_{(i,j-1,k)})^2\\ -(A_{(i,j,k-1),(i,j,k)}/E_{(i,j,k-1)})^2} \tag {38}$

然后Robert Bridson进一步指出可以在不完全Cholesky因子化的基础上进一步做一些提升，引入了Modified Incomplete Cholesky因子化，简称为MIC因子化。只需要在原来的IC因子化的基础上做一些简单修改，算法的收敛复杂度就从原来的$O(n)$降到了$O(n^{1/2})$，假设我们的欧拉网格宽度为$n$个格子。MIC因子化不再直接丢弃在A中相应位置为零的非零矩阵元素，而是考虑将这些非零元素加到对角线的元素上。

MIC因子化同样地构建一个下三角矩阵$K$，只不过此时$KK^T$每一行矩阵元素之和等于矩阵$A$的每一行元素之和。矩阵$K$同样是公式$(37)$的形式，只不过对角矩阵$E$的计算公式稍微有点差异：

$E_{(i,j)}=\sqrt{ A_{(i,j),(i,j)} -(A_{(i-1,j),(i,j)}/E_{(i-1,j)})^2 -(A_{(i,j-1),(i,j)}/E_{(i,j-1)})^2\\ -A_{(i-1,j),(i,j)}A_{(i-1,j),(i-1,j+1)}/E^2_{(i-1,j)} -A_{(i,j-1),(i,j)}A_{(i,j-1),(i+1,j-1)}/E^2_{(i,j-1)} } \\ E_{(i,j,k)}=\sqrt{ A_{(i,j,k),(i,j,k)}-(A_{(i-1,j,k),(i,j,k)}/E_{(i-1,j,k)})^2\\ -(A_{(i,j-1,k),(i,j,k)}/E_{(i,j-1,k)})^2 -(A_{(i,j,k-1),(i,j,k)}/E_{(i,j,k-1)})^2\\ -A_{(i-1,j,k),(i,j,k)} \times (A_{(i-1,j,k),(i-1,j+1,k)}+A_{(i-1,j,k),(i-1,j,k+1)}) /E^2_{(i-1,j,k)}\\ -A_{(i,j-1,k),(i,j,k)} \times (A_{(i,j-1,k),(i+1,j-1,k)}+A_{(i,j-1,k),(i,j-1,k+1)}) /E^2_{(i,j-1,k)}\\ -A_{(i,j,k-1),(i,j,k)} \times (A_{(i,j,k-1),(i+1,j,k-1)}+A_{(i,j,k-1),(i,j+1,k-1)}) /E^2_{(i,j,k-1)} } \tag {39}$

MIC背后的数学原理是傅里叶分析，这里就不仔细展开了。在实际的实现中，为了有更佳的性能表现，我们混合使用IC因子化和MIC因子化，给MIC中增加的项乘上一个权重，通常取$0.97$或者更大。下图5展示计算对角矩阵$E$的伪代码，除了用e存储对角矩阵$E$之外，我们用precon存储$E$的开根倒数。

图5 计算对角矩阵E

计算得到了precon之后，我们就将其应用预处理共轭梯度算法当中，这个预处理得到的下三角矩阵$K$被用于图4伪代码中的$z$向量，图4的伪代码中直接写出$z=M^{-1}r$，这是为了表示求解方程$Mz=r$。实际上我们并不是直接求$M$的逆矩阵，而是将$M$因子化成三角矩阵的乘积$KK^T$，变成了求解$K(K^Tz)=r$，因为$K$和$K^T$分别为下三角矩阵和上三角矩阵，因此我们可以分成两步来求解：首先求解$Kq=r$，直接前向替换即可；然后求解$K^Tp=q$，直接后向替换即可。具体的伪代码如下图6所示。

图6 应用因子化的矩阵

四、不可压缩投影

最后，流体的不可压缩投影$project(\Delta t, \vec u)$算法流程如下所示：

Calculate the negative divergence $b$ （the right-hand side）with modifications at solid wall boundaries.
Set the entries of $A$ (stored in Adiag, etc.).
Construct the preconditioner (either MIC(0) for single threaded solves, or a more complicated domain decomposition set up for parallel solves).
Solve $Ap=b$ with PCG（Preconditioned conjugate gradient）.
Compute the new velocities $\vec u^{n+1} $according to the pressure-gradient update to $\vec u$.