偶然在知乎上看到图形学大佬的几篇关于二维渲染绘制的文章，感觉非常有趣。与普通的光线求交不同，这里的二维渲染采用了光线步进法和符号距离场。下图就是渲染出来的效果，二维虽然少了一维，但渲染开销依旧大，渲染下面的这张图开启了多线程也花费了1个半小时多的时间。

  • 二维渲染
  • SDF构造实体几何
  • 比尔-郎伯定律
  • 实现效果
  • 参考资料
2D Lighting
  偶然在知乎上看到图形学大佬的几篇关于二维渲染绘制的文章，感觉非常有趣，二维的相对而言比较简单但是涉及到的知识也不少，遂记录下来一些自己的学习总结。一些内容跟前面光线追踪的重合了，所以就不细细展开了。本文主要是关于SDF方面的内容。 ## 一、二维渲染   我们要绘制的世界是一个二维的场景，场景中有发光的二维体。对于一个二维屏幕上的像素，我们要求在360度方向上接收的光照值，故给定二维空间的坐标$(x,y)$，渲染方程为对$[0,2\pi]$方向的单重积分： $$ L_o(x,y)=\int_0^{2\pi}L_i(x,y,\theta)d\theta \tag {1} $$   在这里我们就对二维图像的每个像素求解方程$(1)$的积分公式，用tbb多线程库加速渲染，然后将像素矩阵用stb_image保存成png文件。原点在图像的左上角。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
unsigned char * Renderer::render()
{
	parallel_for(blocked_range<size_t>(0, m_height * m_width, 5000),
		[&](blocked_range<size_t>& r)
	{
		for (size_t i = r.begin(); i != r.end(); ++i)
		{
			size_t col = i % m_width;
			size_t row = i / m_width;
			glm::vec3 color(0.0f);
			// sampling and lighting.
			color.x = color.y = color.z =
				sample(static_cast<float>(col) / m_width, static_cast<float>(row) / m_height);

			// save to pixel.
			drawPixel(row, col, color);
		}
	});

	return m_image;
}
  由于被积函数$L(x,y,\theta)$并没有一个显示的数学表达式，我们无法求解公式$(1)$单重积分的解析解，因此采用蒙特卡洛数值积分法。我们首先考虑随机均匀采样$N$个方向，每个方向用$\theta_1,\theta_2,...,\theta_N$表示，因为是均匀采样，所以概率密度函数$pdf=\frac {1}{2\pi}$，蒙特卡洛数值积分公式如下： $$ L_o(x,y)=\frac 1N\Sigma_{i=1}^N\frac{L_i(x,y,\theta)}{\frac{1}{2\pi}} =\frac {2\pi}N\Sigma_{i=1}^N{L_i(x,y,\theta)} \tag {2} $$   因此一个随机均匀采样的蒙特卡洛积分如下所示，此外在这里我们不考虑实际单位，所以实现时把系数$2\pi$去掉了。 
1
2
3
4
5
6
7
8
9
10
11
float Renderer::sample(float x, float y)
{
	float sum = 0.0f;
	for (int i = 0; i < m_samples; ++i)
	{
		// randome sampling.
		float angle = M_2PI * rand() / RAND_MAX;
		sum += trace(x, y, cosf(angle), sinf(angle));
	}
	return  sum / m_samples;
}
  紧接着我们将实现trace函数，这个函数返回给定方向上的光照值。我们采用光线步进法（Ray Marching），场景中的物体以符号距离场（Signed Distance Field，简称SDF）表示，符号距离场是一个这样的映射：$\phi:R^2\to R$，具有如下的性质：   (1).当$\phi(x)>0$时，坐标$x$位于场景的物体外面，$x$到最近物体表面的距离为$\phi(x)$；   (2).当$\phi(x)<0$时，坐标$x$位于场景的物体里面，$x$到最近物体表面的距离为$-\phi(x)$；   (3).当$\phi(x)="0$时，坐标$x$恰好位于场景的物体表面上。"   一个圆心为$c$、半径为$r$的圆盘sdf为： $$ \phi_{disk}(x)="||x-c||-r" \tag {3} 
1
2
3
4
5
float Renderer::circleSDF(float x, float y, float cx, float cy, float radius)
{
	float ux = x - cx, uy = y - cy;
	return sqrtf(ux * ux + uy * uy) - radius;
}
  目前我们的场景只有一个发光的圆盘，圆心位于$(0.5, 0.5)$，半径大小为$0.1$，向各个方向发射2个单位的光。我们采样光线步进法进行追踪，给定起始点$(x,y)$，每一步我们计算符号距离场，若符号距离场给出的值依然在物体的外面，我们按照符号距离场的值（也就是点$(x,y)$到物体表面的最近距离长度）移动点$(x,y)$，依次迭代下去，直到达到物体表面或里面，或者达到最大的迭代次数、最长步进距离。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
float Renderer::trace(float ox, float oy, float dx, float dy)
{
	float step = 0.0f;
	int maxIter = 10;
	float maxDistance = 2.0f;
	float epsilon = 1e-6f;
	for (int i = 0; i < maxIter && step < maxDistance; ++i)
	{
		float sdf = circleSDF(ox + dx * step, oy + dy * step, 0.5f, 0.5f, 0.1f);
		// reach the egde(==0) or inside(<0)
		if (sdf < epsilon)
			return 2.0f;
		step += sdf;
	}
	return 0.0f;
}
  我们设定随机均匀的采样数为$64$，则运行程序得到下面的结果：
图1 随机均匀采样

  渲染的结果有很多明显的噪声点，这是因为我们的蒙特卡洛数值积分方法做了一个比较少数量的随机采样，导致积分估值的误差比较。增大采样数量能够使得结果更精确，噪声点减少，下图2显示了不同采样次数下的渲染结果，可以看到随着采样次数的增大，渲染出现的噪声点越来越说。但是随着采样次数的采样，算法耗费的时间也呈线性增长。为了能够在低采样数时依然获取较好的结果，我们从改进采样方法入手。

图2 32次、128次、512次、2048次随机采样

  一种采样方法就是分层采样（Stratified sampling），这种采样方法不再随机，而是将采样的范围做一个等分，划分成$N$个区间，在每个区间采样一个确定而非随机的值。这种方法实际上就是非随机的均匀采样。这里我们将$[0,2\pi]$划分成$N$个区间，每个区间获取一个采样方向。在sample函数里修改一行代码即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
float Renderer::sample(float x, float y)
{
	float sum = 0.0f;
	for (int i = 0; i < m_samples; ++i)
	{
		// randome sampling.
		// float angle = M_2PI * rand() / RAND_MAX;
		// stratified samping.
		float angle = M_2PI * i / m_samples;
		sum += trace(x, y, cosf(angle), sinf(angle));
	}
	return  sum / m_samples;
}

  采样了分层采样获取的结果如下图3所示，看起来还不错，渲染的结果不再有噪声点，此时的采样数量仅为$64$。但是分层采样渲染出来的效果太过规律了，很明显的几何分割痕迹，因此为了更好地获取渲染效果，我们将采用另外一种采样方法——抖动采样（Jittered Sampling）。

图3 分层采样

  抖动采样方法就是将均匀随机采样和分层采样这两种方法结合在一起，首先将采样范围分成$N$个区间，在每个区间做均匀的随机采样，这就是抖动采样方法的思想，非常简单。同样我们只需在sample函数修改一行即可：

1
2
// jittered sampling.
float angle = M_2PI * (i + static_cast<float>(rand()) / RAND_MAX) / m_samples;

图4 抖动采样

  上图4就是抖动采样获取的效果，采样数量同样为$64$个。可以看到，对比随机采样和分层采样，抖动采样获取的效果要好上不少。这里还有一点就是我们采样的随机数都是系统生成的伪随机数，相对而言均匀性较差，因此可以考虑前面一篇提到的低差异性随机数，占个坑，以后来填。

二、SDF构造实体几何

  SDF是一个非常有用的工具，它通过一个函数来显式地表达几何形状。满足SDF函数$\Phi(x)\leq 0$的$x$点集，构成了该SDF所表达的几何体的封闭空间。我们还可以通过不同SDF函数之间进行集合运算构建出各种各样不同形状的几何体，这个就是SDF的强大之处。SDF的三个基本运算为并集、交集和相对补集，分别如下所示：

  直接看上面的数学公式可能没有那么直观，我们可以通过围绕SDF构成了封闭空间为中心展开。

  两个SDF函数的求并集运算就是将两个几何体构成的封闭空间（或者封闭空间中的点的集合）取并集，此时在几何体内的点$x$应满足$\Phi_A(x)\leq 0$或者$\Phi_B(x)\leq 0$，SDF值取最小的那个，这是因为两个SDF取并集时它们的几何体构成了一个整体，我们应该取到这个整体的最近表面的距离长度。

1
2
3
4
Result SDF::unionOperation(Result a, Result b)
{
	return a.sdf < b.sdf ? a : b;
}

  两个SDF函数的求交集运算就是将两个几何体构成的封闭空间取交集，此时在几何体内的点$x$应满足$\Phi_A(x)\leq 0$且$\Phi_B(x)\leq 0$，SDF值取最大的那个，这是因为在几何体内的点其SDF函数值为负数，负数越大则其绝对值表示的距离越小。

1
2
3
4
5
6
Result SDF::intersectOperation(Result a, Result b)
{
	Result ret = a.sdf > b.sdf ? b : a;
	ret.sdf = a.sdf > b.sdf ? a.sdf : b.sdf;
	return ret;
}

  两个SDF函数的相对补集就将第一个几何体构成的封闭空间减去第一个几何体与第二个几何体相交区域，此时在几何体内的点应满足$\Phi_A(x)\leq0$且$\Phi_B(x)\geq 0$，这个就相当于取$B$的补集，然后取$A$与$B$的补集之间的交集。$B$的补集就是取其SDF函数的相反数。

1
2
3
4
5
6
7
Result SDF::subtractOperation(Result a, Result b)
{
	Result ret;
	ret.emissive = a.emissive;
	ret.sdf = (a.sdf > -b.sdf) ? a.sdf : -b.sdf;
	return ret;
}

  通过以上的三个SDF基本运算以及圆盘的SDF函数，我们就可以组合出一些比较新奇的几何体了。下面是两个不同场景的构建代码。第一个场景有三个发光圆盘，利用并集运算把它们全部囊括到场景中。第二个场景是两个有重合区域的发光圆盘使用不同的SDF运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Result Scene::threeEmissiveSphereScene(float x, float y)
{
	Result ret1 = { SDF::circleSDF(x,y,0.3f,0.3f,0.1f),glm::vec3(2.0f) };
	Result ret2 = { SDF::circleSDF(x,y,0.3f,0.7f,0.05f),glm::vec3(0.8f) };
	Result ret3 = { SDF::circleSDF(x,y,0.7f,0.5f,0.1f),glm::vec3(0.0f) };
	return SDF::unionOperation(SDF::unionOperation(ret1, ret2), ret3);
}

Result Scene::moonEmissiveScene(float x, float y)
{
	Result ret1 = { SDF::circleSDF(x,y,0.4f,0.5f,0.20f), glm::vec3(1.0f) };
	Result ret2 = { SDF::circleSDF(x,y,0.6f,0.5f,0.20f),glm::vec3(0.8f) };
	//return SDF::unionOperation(ret1, ret2);
	return SDF::intersectOperation(ret1, ret2);
	//return SDF::subtractOperation(ret1, ret2);
}

图5 sdf构建的几何实体

  上图5展示了几个组合不同SDF运算构建的几何实体，可以看到通过相对补集运算，我们可以构建一个月牙形状的几何体。此外还需要提一点的是，上图已经出现了阴影效果，这是因为我们在光线步进时触碰到几何体时不在往前步进，因此导致了几何遮蔽，几何体后方接收的光照强度相对较弱，从而产生阴影。

  除了圆盘的SDF，接下来我们构建其他一些常见的几何体。首先来看下圆盘的SDF，即公式$(3)$，可以看到圆盘的SDF就是坐标$x$与圆心$c$的欧式距离再减去$r$，这个减去$r$非常关键，通过减去$r$我们把圆心点$c$扩展成半径为$r$的圆盘。实际上，对于任意形状几何体的SDF，减去一个常数$r$，都相当于把该几何体的封闭空间向外扩展$r$大小的范围。下面我们将使用这个特性。

  首先是平面的SDF，但是在二维空间中平面退化成了直线。在二维空间中，直线将二维空间划分成了两个无穷大的两个平面。直线可用直线上的一点$p$和及其法线向量$n$来定义，对于直线上的任意一点$x$：

  位于直线上方的点$(x-p)\cdot n>0$，下方的点$(x-p)\cdot n<0$，故直线的符号距离场函数为：

1
2
3
4
float SDF::planeSDF(float x, float y, float px, float py, float nx, float ny)
{
	return (x - px)*nx + (y - py)*ny;
}

  然后是胶囊条状的几何体。如下图所示，胶囊条用点$a$和$b$以及半径$r$来表示。胶囊几何体的SDF就等价于线段$ab$的SDF再减去$r$（即扩大$r$半径）。

图6 胶囊几何体

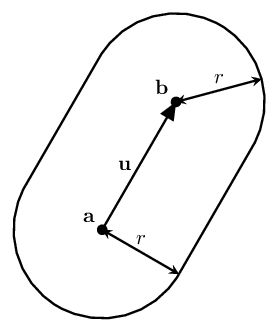
  线段的SDF就是计算一点$x$到该线段的距离，我们通过把$x$点投影到线段的延长线上，然后再将投影点$x’$限制在线段的范围内，因为有可能投影点在线段之外。如下图7所示。

图7 投影点x'

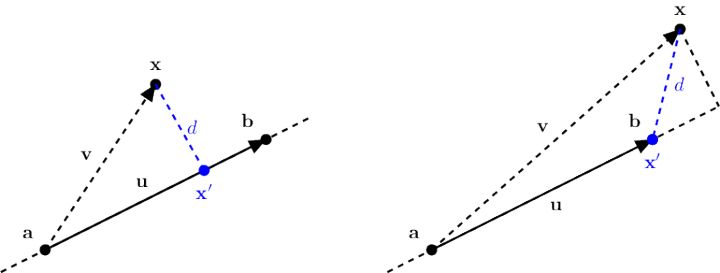
  然后距离场就为$||x-x’||$：

1
2
3
4
5
6
7
8
float SDF::segmentSDF(float x, float y, float ax, float ay, float bx, float by)
{
	float vx = x - ax, vy = y - ay;
	float ux = bx - ax, uy = by - ay;
	float t = fmaxf(fminf((vx * ux + vy * uy) / (ux * ux + uy * uy), 1.0f), 0.0f);
	float dx = vx - ux * t, dy = vy - uy * t;
	return sqrtf(dx * dx + dy * dy);
}

  胶囊几何体在线段的基础上，在向外扩展半径$r$大小的范围：

1
2
3
4
float SDF::capsuleSDF(float x, float y, float ax, float ay, float bx, float by, float radius)
{
	return segmentSDF(x, y, ax, ay, bx, by) - radius;
}

  紧接着我们来实现矩形的SDF，我们把矩形当作一个定向的包围盒，由中心点$c$、旋转角$\theta$和半长$s$表示。

图8 矩形SDF

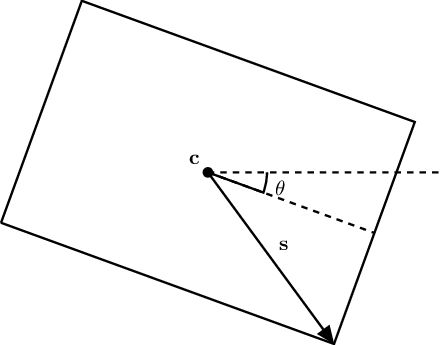
  基本思路就是将SDF函数的输入$x$变换到OBB的坐标系。我们知道从OBB坐标系的$x’$转换到世界空间的$x$，其变换矩阵如下所示，需要注意我们的y轴正向是朝下的。

  那么反过来从$x$到$x’$就是上面的逆过程，旋转矩阵为正交矩阵，其逆矩阵就是转置矩阵。

  同时由于矩形具有对称性，我们仅考虑第一象限。

1
2
3
4
5
6
7
8
float SDF::boxSDF(float x, float y, float cx, float cy, float theta, float sx, float sy)
{
	float cosTheta = cosf(theta), sinTheta = sinf(theta);
	float dx = fabs((x - cx) * cosTheta + (y - cy)*sinTheta) - sx;
	float dy = fabs((y - cy) * cosTheta - (x - cx)*sinTheta) - sy;
	float ax = fmaxf(dx, 0.0f), ay = fmaxf(dy, 0.0f);
	return fminf(fmaxf(dx, dy), 0.0f) + sqrtf(ax * ax + ay * ay);
}

  最后就是三角形的SDF，三角形可以用三个线段来表示，我们先计算点到三个线段的最小距离，然后判断点是在三角形里面还是外面来判断距离的符号。我们采用环绕顺序来判断内外情况。

1
2
3
4
5
6
7
8
9
10
11
float SDF::triangleSDF(float x, float y, float ax, float ay, float bx, float by, float cx, float cy)
{
	float d = fminf(fminf(
		segmentSDF(x, y, ax, ay, bx, by),
		segmentSDF(x, y, bx, by, cx, cy)),
		segmentSDF(x, y, cx, cy, ax, ay));
	return 
		(bx - ax) * (y - ay) > (by - ay) * (x - ax) &&
		(cx - bx) * (y - by) > (cy - by) * (x - bx) &&
		(ax - cx) * (y - cy) > (ay - cy) * (x - cx) ? -d : d;
}

  下图9就是我们实现的几个SDF几何体。

图9 SDF几何体

三、比尔-郎伯定律

  本文实现的本质上就是一个二维的光线追踪器，关于反射、折射以及菲涅尔定律前面都已经提及过，这里不再赘述。采用SDF进行光线步进来追踪光线有个问题，就是如何获取几何点上的法线向量。我们的几何体都是采用一个函数来表示，法线的获取的肯定与这个函数密切相关。在SDF构建的几何体边界，距离场变化最大的方向就是法线方向，距离长变化最大的方向就是SDF函数的梯度：

  这里我们采用中心差分法求梯度的数值近似，中心差分法在前面流体模拟相关文章已提及多次：

  中心差分法对于锯齿函数等这类不连续的函数存在着严重的零域问题，但是我们的SDF通常是一个连续的函数，因此不用担心中心差分法在此处出现严重错误。

1
2
3
4
5
void Renderer::gradient(float x, float y, float & nx, float &ny)
{
	nx = (scene(x + EPSILON, y).sdf - scene(x - EPSILON, y).sdf) * (0.5f / EPSILON);
	ny = (scene(x, y + EPSILON).sdf - scene(x, y - EPSILON).sdf) * (0.5f / EPSILON);
}

  然后这里要提一下的就是透射问题，这个透射在之前的三维光线追踪渲染器中没有涉及到。透射在生活中很常见，一个例子就是大气层的透射导致天空呈现蓝色。这里要介绍关于透射的一个定律——比尔郎伯定律（Beer-Lambert law），它描述了电磁波（例如可见光）通过物体时，物体吸收部分电磁波，吸收的程度与物体的厚度、物质的消光系数和浓度密切相关，透射率计算公式如下：

  $T\in[0,1]$即为透射率，$\alpha’$为物体的消光系数，通常与波长有关，因而是一个RGB向量。而$c\in [0,\infty)$是浓度，$d\in[0,\infty)$是光程距离。我们实现的物质是均匀的，因而$\alpha’$和$c$是一个常量，我们把这两个合并为一个，在光线步进的结果中新增一条消光率absorption。

1
2
3
4
5
6
7
8
struct Result
{
	float sdf;
	glm::vec3 emissive;
	float reflectivity;
	float eta;
	glm::vec3 absorption;
};

  在计算透射率时就输入消光率absorption和光程距离，返回透射率。

1
2
3
4
glm::vec3 Renderer::beerLambert(glm::vec3 a, float d)
{
	return glm::vec3(expf(-a.x * d), expf(-a.y * d), expf(-a.z * d));
}

  在追踪的过程中，将最终的结果再乘上这个透射率，这样就能实现透明的有色水晶。透明水晶呈现不同的颜色是因为光透光水晶时，一些波长的光被吸收，剩下的光波形成颜色，从而呈现水晶有颜色一样。下图10展示了实现的几个水晶宝石，非常漂亮。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
glm::vec3 Renderer::trace(float ox, float oy, float dx, float dy, int depth)
{
	float step = 1e-3f;
	float sign = scene(ox, oy).sdf > 0.0f ? 1.0f : -1.0f;
	for (int i = 0; i < MAXITER && step < MAXDIST; ++i)
	{
		float x = ox + dx * step;
		float y = oy + dy * step;
		Result ret = scene(x, y);
		// reach the egde(==0) or inside(<0)
		if (ret.sdf * sign < EPSILON)
		{
            // reflect and refract.
			....
            
            // beer-lambert law.
			return sum * beerLambert(ret.absorption, step);
		}
		step += ret.sdf * sign;
	}
	return glm::vec3(0.0f);
}

图10 几种水晶宝石

四、实现效果

参考资料：

$[1]$ 用 C 语言画光（一）：基础

$[2]$ 用 C 语言画光（二）：构造实体几何

$[3]$ 用 C 语言画光（三）：形状

$[4]$ 用 C 语言画光（七）：比尔-朗伯定律

 上一页

Computer Graphics Fluid Simulation

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 ， 总访问量为 次 。
载入天数...载入时分秒...