流体渲染Fluid Rendering：基于屏幕空间的液体渲染

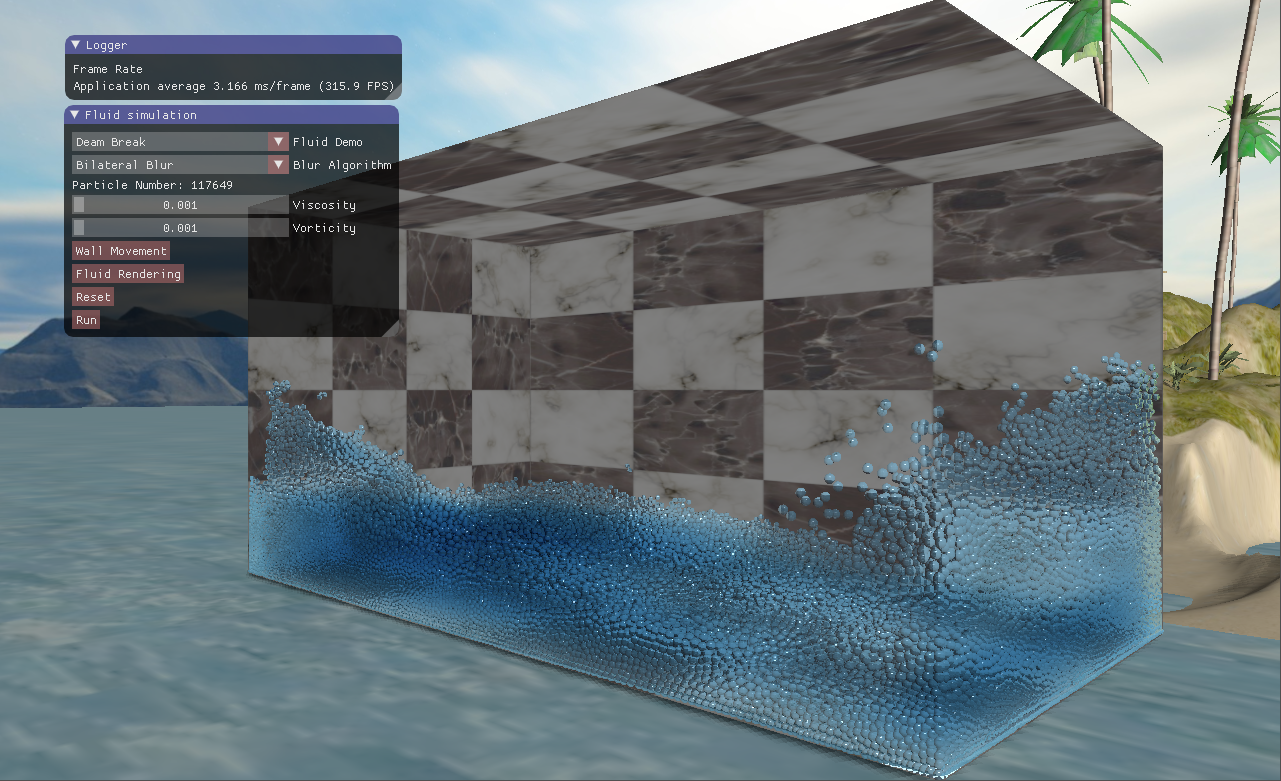
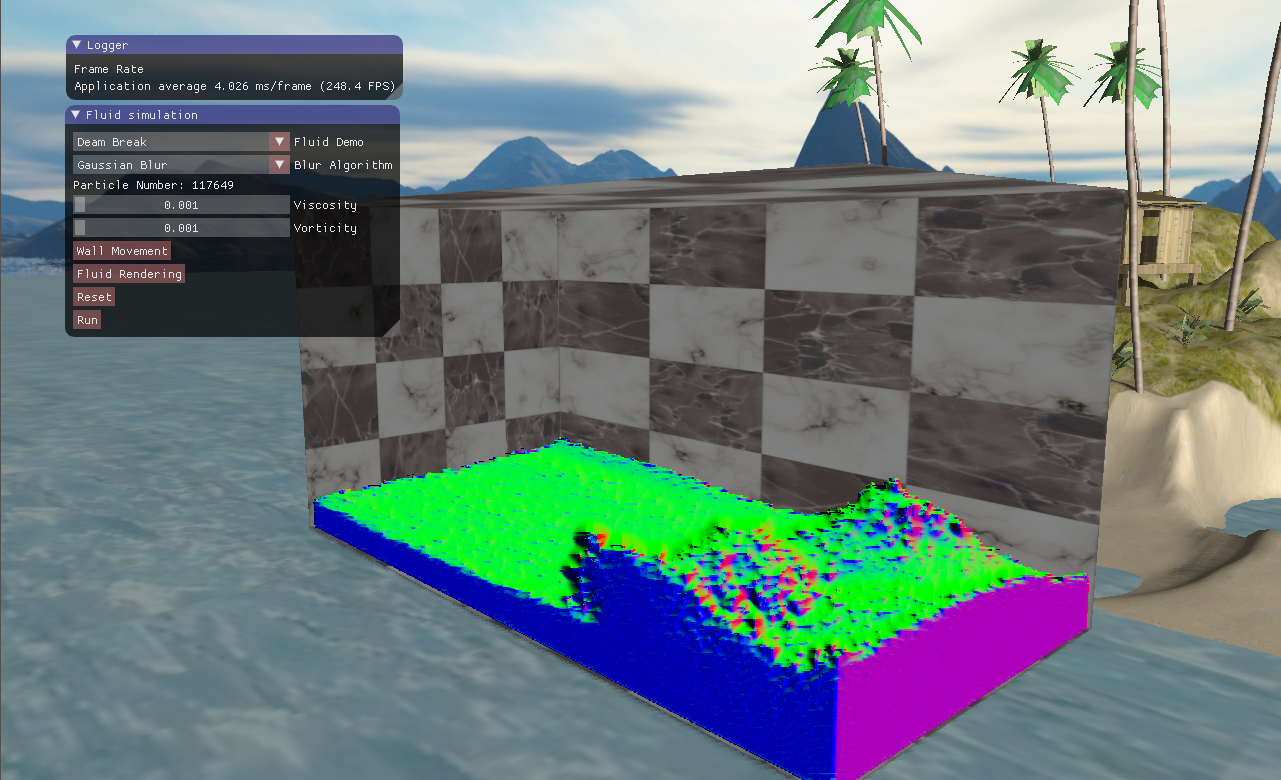
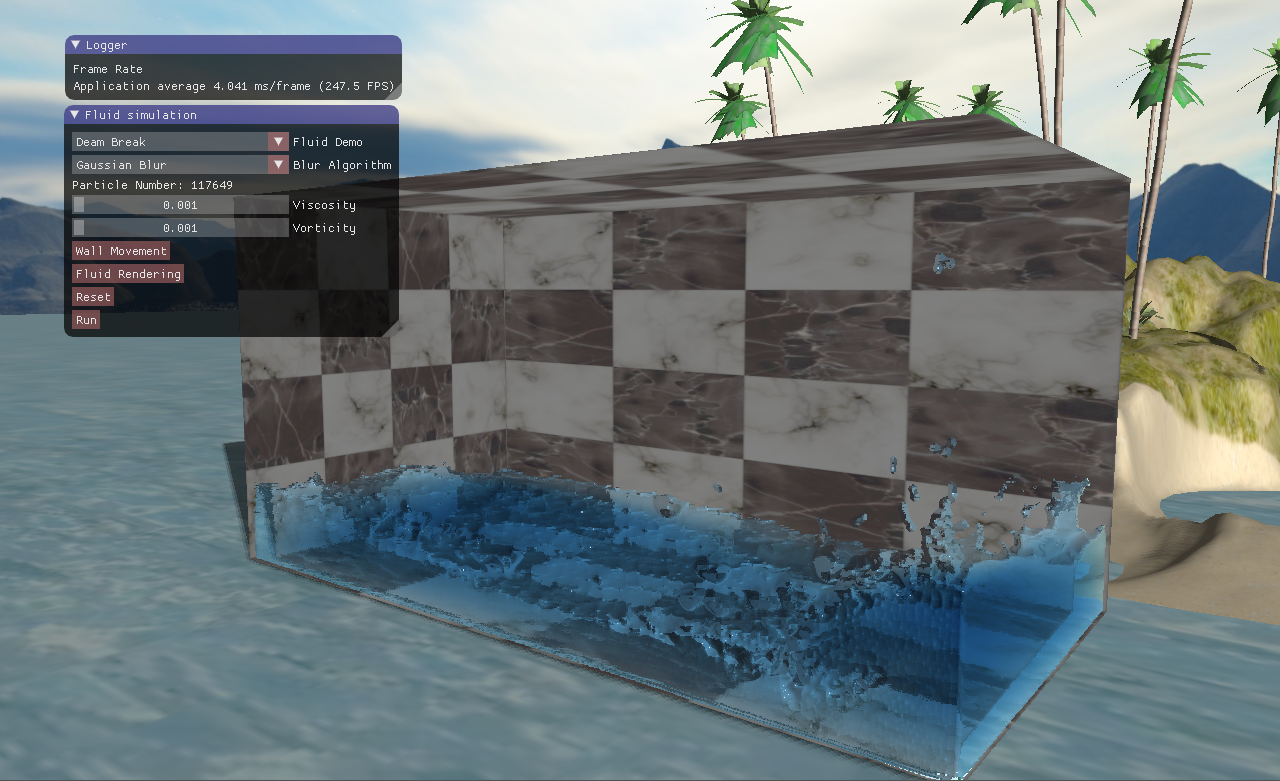
本文主要是关于屏幕空间的液体渲染算法，分别介绍了高斯滤波、双边滤波和曲率流方法平滑流体深度的方法。

• 基于屏幕空间的流体渲染
• 水体的光照计算
• 流体深度贴图的平滑处理
• 实现效果
• 参考资料

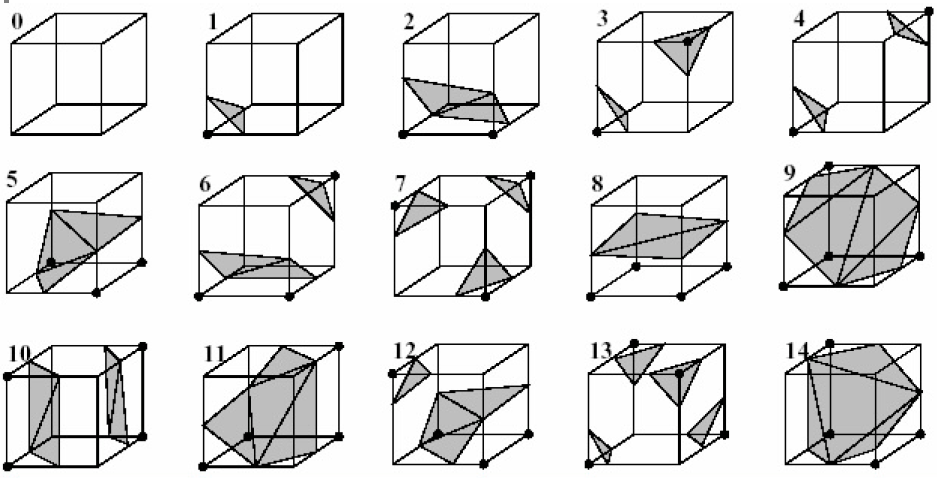
基于屏幕空间的流体渲染

  在计算机图形学中，我们最后都要把模拟的物体渲染出来，这是图形学的最终目的。而目前对于流体渲染，无论是基于拉格朗日视角的还是基于欧拉视角的流体模拟都要经过流体表面重建这一步，然后再做进一步的光照着色计算。流体表面重建有个非常经典的算法——Marching Cubes$^{[2]}$，该方法采用水平集（Level Set），首先将空间划分称均匀的立方体网格，然后计算每个网格上8个顶点的密度。对于每一个立方体，如果立方体上的一条边两个端点的密度值大于给定的一个阈值$\rho_{boundary}$，则这条边上存在着一个流体表面上的顶点。最后将每个立方体构造的多边形拼接，即可得到流体的表面网格。该方法基于这样的一个事实：流体表面处的密度应该等于某个固定的值，流体表面是一个三维的密度等高面，密度值为$\rho_{boundary}$，这就是水平集的思想。

图1 Marching Cube的15种模式

  Marching Cube是流体表面重建的传统做法，实现效果非常不错，但是算法的时间复杂度大，重建一次需要花费不少的时间。对于流动的流体来说，需要每帧构建流体表面，因而很难保证实时性。除了Marching Cube这类传统的流体表面重建方法，还有一些技巧性比较强的方法适合实时性应用，基于屏幕空间的流体渲染方法就是这一类。基于屏幕空间的流体渲染以一种新的思路角度展开流体的渲染，这种方法对并行友好，不涉及到直接对液体表面网格的重建，实现也相对简单。

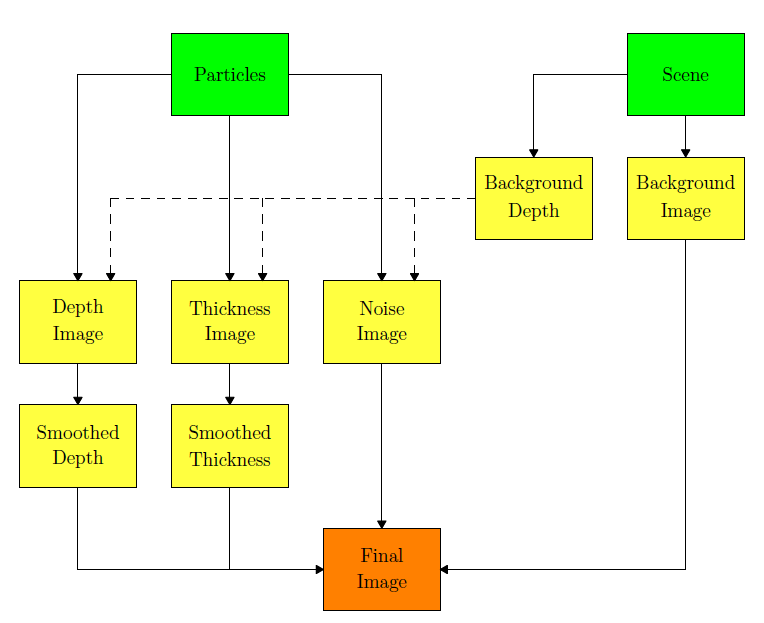
一、基于屏幕空间的流体渲染

  首先介绍一些基于屏幕空间的流体渲染算法纵览。与在世界空间构建流体表面网格的思路不同，基于屏幕空间的流体渲染算法直接在屏幕空间做流体表面的复原工作，操作维度从三维降到了二维。这是一种与图形处理紧密结合的渲染算法。算法分为两个步骤，重点在于第一个步骤。第一个步骤是屏幕空间流体处理步骤，首先将流体粒子按照当前的投影矩阵和视图矩阵渲染到屏幕空间，获取流体粒子的深度轮廓信息、流体厚度信息，这些信息存储到纹理中，紧接着我们对存储深度信息的纹理做一些后处理操作，模糊掉球形粒子的坑坑洼洼，使得深度信息更为平滑，最后我们根据深度纹理和厚度纹理做流体的光照计算。

图2 Screen Space Fluid Rendering算法总览

  算法的总流程如图2所示，其中的噪声图像生成不是必须的，实际上我觉得加上这个噪声处理反而是个败笔。对于水体来说，它的表面通常是比较光滑的而不是坑坑洼洼。背景图用于处理流体的折射计算，因此流体通常应该放到最后渲染。该算法可以看成是针对流体的延迟渲染，流体的表面法线信息并不能直接获得，需要从深度贴图中重建法线，而在这之前深度贴图也要经过一些特殊的处理。基于屏幕空间的流体渲染步骤中，如何对深度贴图做处理使之能真实反映流体的特性是算法的核心，剩下的光照部分直接采用Blin-Phong光照模型，并综合考虑水体的折射和反射，上面提到的厚度贴图用于水体的折射计算，因为越厚的流体其透光率越低。

二、水体的光照计算

  首先我们先实现一个不对深度贴图和厚度贴图做处理的Naive版的流体渲染算法，这有利于我们弄清整个算法的思路，而且使得实现的过程更加清晰、有条理、便于调试。去掉对深度贴图和厚度贴图的处理部分（噪声部分我们不考虑），剩下的算法流程就分为：渲染不包含流体的场景纹理、渲染粒子深度信息、渲染粒子厚度信息、光照着色计算。这里我们采用OpenGL的render to target，将场景、深度贴图、厚度贴图都渲染到纹理当中，供最后的光照着色计算使用。

  一开始我们为了获取流体的深度信息和厚度信息，需要流体以球形粒子的形态进行绘制，这里我们采用OpenGL的点精灵Point Sprite做粒子绘制。在OpenGL中，点精灵Point Sprite就是一个内建的始终朝向摄像机视角的正方形，我们可以指定它的大小，但是它的大小是定义在屏幕空间的。因此，在利用点精灵绘制流体粒子时，一方面我们要根据世界空间的流体粒子大小设置点精灵的大小，另一方面要以将四边形变成圆形。

  首先根据世界空间的流体粒子大小设置点精灵的大小，上面说了，点精灵的大小是定义在屏幕空间的，而通常我们设置的流体粒子大小是世界空间的。为了正确设置点精灵的大小，使之符合透视原理，需要计算世界空间的长度投影到屏幕空间的长度，这个比较基础，根据三角形相似的原理即可。

// calculate particle size scale factor.
float aspect = camera->getAspect();
float fovy = camera->getFovy();
float pointScale = 1.0f * m_screenWidth / aspect * (1.0f / tanf(glm::radians(fovy) * 0.5f));

......
shader->setFloat("pointScale", pointScale);
shader->setFloat("pointSize", m_particleRadius);

......
#version 430 core
layout (location = 0) in vec4 position;

uniform mat4 modelMatrix;
uniform mat4 viewMatrix;
uniform mat4 projectMatrix;
uniform float pointScale;
uniform float pointSize;

out vec3 eyeSpacePos;

void main(){
	eyeSpacePos = (viewMatrix * modelMatrix * vec4(position.xyz, 1.0f)).xyz;
	gl_PointSize = -pointScale * pointSize / eyeSpacePos.z;
	gl_Position = projectMatrix * viewMatrix * modelMatrix * vec4(position.xyz, 1.0f);
}

  然后就是让正方形的点精灵变成一个圆形。在片元着色器中，点精灵提供了一个gl_PointCoord变量，这是一个内建的专用于点精灵的纹理坐标，已经经过光栅化插值之后的点精灵纹理坐标。我们根据这个坐标来获取每一个点精灵的像素所在的相对位置，gl_PointCoord纹理坐标以左上角为原点，我们需要将其变换到点精灵中心。接着获取每个像素的法线信息，并计算半径长度，半径超过1.0的像素我们给它discard掉。

#version 430 core

uniform float pointSize;
uniform mat4 projectMatrix;

in vec3 eyeSpacePos;

void main(){	
	vec3 normal;
	normal.xy = gl_PointCoord.xy * vec2(2.0, -2.0) + vec2(-1.0,1.0);
	float mag = dot(normal.xy, normal.xy);
	if(mag > 1.0) discard;
	normal.z = sqrt(1.0 - mag);

	......
}

  点精灵给我们提供一个非常方便的球心粒子绘制方法，这种方法绘制的球体是基于解析解的，精度非常高，球体非常光滑，而如果采用球体网格则需要绘制很多个网格，球体精度受限于网格的精度，速度也慢。现在知道如何根据点精灵绘制，接下来我们需要从流体粒子中获取深度贴图和厚度贴图。

1、流体深度贴图

  绘制流体深度贴图需要开启深度测试，并创建一个帧缓冲，深度的信息绘制到给定帧缓冲的深度缓冲当中。

void LiquidDrawable::drawLiquidDepth(Camera3D::ptr camera, Light::ptr sunLight,
	Camera3D::ptr lightCamera, Shader::ptr shader)
{
	m_framebuffer->bind();

	// calculate particle size scale factor.
	float aspect = camera->getAspect();
	float fovy = camera->getFovy();
	float pointScale = 1.0f * m_screenWidth / aspect * (1.0f / tanf(glm::radians(fovy) * 0.5f));

	// render state.
	glEnable(GL_DEPTH_TEST);
	glDisable(GL_BLEND);
	glClear(GL_DEPTH_BUFFER_BIT);
	glEnable(GL_PROGRAM_POINT_SIZE);
	glEnable(GL_VERTEX_PROGRAM_POINT_SIZE);

	// shader.
	shader = m_shaderMgr->getShader("liquidDepth");
	shader->bind();
	shader->setFloat("farPlane", camera->getFar());
	shader->setFloat("nearPlane", camera->getNear());
	shader->setFloat("pointScale", pointScale);
	shader->setFloat("pointSize", m_particleRadius);
	shader->setFloat("densityLowerBound", m_densityLowerBound);
	shader->setMat4("modelMatrix", m_transformation.getWorldMatrix());
	shader->setMat4("viewMatrix", camera->getViewMatrix());
	shader->setMat4("projectMatrix", camera->getProjectMatrix());

	// draw
	glBindVertexArray(m_particleVAO);
	glDrawArrays(GL_POINTS, 0, m_numParticles);
	glBindVertexArray(0);

	// restore.
	m_shaderMgr->unBindShader();
	glDisable(GL_PROGRAM_POINT_SIZE);
	m_framebuffer->unBind();

}

  在片元着色器，我们需要计算像素的深度信息，为了还原出粒子的深度信息，我们首先将粒子在摄像机空间的位置传到片元着色器中，这个其实就是点精灵在摄像机空间的中心点。然后计算每个像素的法线，每个像素在摄像机空间的点就等于$eyeSpacePos + normal * pointSize$，其中$pointSize$就是流体粒子的半径大小。得到每个像素在摄像机空间的点，我们再将其乘上投影矩阵，并做透视除法，得到标准化设备空间$[-1,+1]$的深度值。

============vertex   shader================
#version 430 core
layout (location = 0) in vec4 position;

uniform mat4 modelMatrix;
uniform mat4 viewMatrix;
uniform mat4 projectMatrix;
uniform float pointScale;
uniform float pointSize;
uniform float densityLowerBound;

out vec3 eyeSpacePos;

void main(){
	eyeSpacePos = (viewMatrix * modelMatrix * vec4(position.xyz, 1.0f)).xyz;
	gl_PointSize = -pointScale * pointSize / eyeSpacePos.z;
	// to prevent single or a few particles.
	if(position.w < densityLowerBound) 
		gl_PointSize = 0.0f;
	gl_Position = projectMatrix * viewMatrix * modelMatrix * vec4(position.xyz, 1.0f);
}
    
============fragment shader================
#version 430 core

uniform float pointSize;
uniform mat4 projectMatrix;

in vec3 eyeSpacePos;

void main(){	
	vec3 normal;
	normal.xy = gl_PointCoord.xy * vec2(2.0, -2.0) + vec2(-1.0,1.0);
	float mag = dot(normal.xy, normal.xy);
	if(mag > 1.0) discard;
	normal.z = sqrt(1.0 - mag);

	vec4 pixelEyePos = vec4(eyeSpacePos + normal * pointSize, 1.0f);
	vec4 pixelClipPos = projectMatrix * pixelEyePos;
	float ndcZ = pixelClipPos.z / pixelClipPos.w;
	gl_FragDepth = ndcZ;
}

  经过上面的一个pass，我们得到了流体的深度信息。下面是一张近看的流体粒子深度贴图，为什么要近看？因为投影矩阵对深度信息做了一个非线性变换，这个非线性变换使得深度值密度在靠近1.0这一端，稍微远一点，就全白看不见了。（所以如果渲染出来一张全白的深度贴图，不要着急，拉近看看）

图3 流体深度贴图

2、流体厚度贴图

  然后我们需要获取流体的厚度贴图，获取厚度贴图不是必须的，这是因为厚度贴图是为了流体折射计算服务。有些流体并不透光（如牛奶），所以也不存在折射。与渲染流体深度贴图一样，我们以将流体粒子以球形的点精灵形态进行绘制。给定一个方向，流体厚度衡量在这个方向上有多少流体粒子，越多越厚。因此，为了计算流体的厚度，我们采用了OpenGL的blending技巧，也就是透明融合，每个流体粒子计算各自贡献的厚度值，然后将其输出到颜色缓冲中，借助OpenGL的透明融合，将厚度值累积起来，这样就能得到从摄像机方向看去的流体厚度信息。此外，由于我们是采用球形点精灵绘制一个流体粒子，一个流体粒子，其厚度贡献值从中心到边缘应该逐渐减少，为此我们采用计算得到的normal的z分量作为厚度值，并乘上一个缩放系数。具体如下所示：

#version 430 core

uniform float pointSize;
uniform mat4 projectMatrix;

layout(location = 0) out vec4 fragColor;

void main(){	
	vec3 normal;
	normal.xy = gl_PointCoord.xy * vec2(2.0, -2.0) + vec2(-1.0,1.0);
	float mag = dot(normal.xy, normal.xy);
	if(mag > 1.0) discard;
	normal.z = sqrt(1.0 - mag);
	fragColor = vec4(normal.z*0.005, 0.0, 0.0, 1.0);
}

  在CPU端，我们关闭深度测试，开启透明融合，并设置融合函数为additive blending，即加法融合。所谓加法融合，就是原像素值和目标像素值直接相加，不乘上任何的缩放系数。在OpenGL的加法融合就是设置glBlendFunc的参数均为GL_ONE、GL_ONE。这样不同流体粒子之间的厚度值直接叠加，达到我们所需的效果。同时为了凸显厚度，我们设当地设大一点粒子的大小。

void LiquidDrawable::drawLiquidThick(Camera3D::ptr camera, Light::ptr sunLight,
	Camera3D::ptr lightCamera, Shader::ptr shader)
{
	m_framebuffer->bind();

	// calculate particle size scale factor.
	float aspect = camera->getAspect();
	float fovy = camera->getFovy();
	float pointScale = m_screenWidth / aspect * (1.0f / tanf(glm::radians(fovy) * 0.5f));

	// render state.
	glEnable(GL_BLEND);
	glBlendFunc(GL_ONE, GL_ONE);
	glDepthMask(GL_FALSE);
	glEnable(GL_DEPTH_TEST);
	glDisable(GL_DEPTH_TEST);
	glEnable(GL_PROGRAM_POINT_SIZE);
	glEnable(GL_VERTEX_PROGRAM_POINT_SIZE);
	glClearColor(0.0, 0.0, 0.0, 1.0);
	glClear(GL_COLOR_BUFFER_BIT);

	// shader.
	shader = m_shaderMgr->getShader("liquidThick");
	shader->bind();
	shader->setFloat("pointScale", pointScale);
	shader->setFloat("pointSize", 4.0f * m_particleRadius);
	shader->setMat4("modelMatrix", m_transformation.getWorldMatrix());
	shader->setMat4("viewMatrix", camera->getViewMatrix());
	shader->setMat4("projectMatrix", camera->getProjectMatrix());

	// draw
	glBindVertexArray(m_particleVAO);
	glDrawArrays(GL_POINTS, 0, m_numParticles);
	glBindVertexArray(0);

	// restore.
	glDepthMask(GL_TRUE);
	glDisable(GL_BLEND);
	glDisable(GL_PROGRAM_POINT_SIZE);
	m_shaderMgr->unBindShader();
	m_framebuffer->unBind();
}

图4 流体厚度贴图

  图4就是渲染出来的流体厚度贴图，越红的地方越厚。

3、水体折射、Blin-Phong光照

  在前面的步骤我们获取了两张纹理贴图：流体深度纹理、流体厚度纹理。然后我们需要根据这两张纹理计算水体的光照效果。前面已经提到过，这是一种类似于延迟渲染的技术，光照计算都是在屏幕空间的四边形上进行。我们首先要根据流体的深度纹理信息重建流体表面的法线向量。在屏幕空间中，我们已知当前像素的纹理坐标，和对应的流体深度信息，那么如何根据这些信息重建法线向量呢？这就涉及到了如何从设备标准空间ndc顶点转换到摄像机空间$^{[1]}$。

  设摄像机空间的顶点坐标为$(vx,vy,vz,vw)$，其中$vw=1.0$，ndc空间的顶点坐标为$(nx,ny,nz)$，其中$x、y、z\in[-1,+1]$。我们知道从摄像机空间变换到ndc空间，需要经过投影变换、透视除法这两个步骤：

$$clip=projectMatrix \cdot (vx,vy,vz,1.0)\\ (nx,ny,nz) = clip.xyz/clip.w \tag {1}$$

  其中的clip就是裁剪空间的顶点坐标。所以我们的问题就是，已知ndc空间的$(nx,ny,nz)$、摄像机空间的$vw=1.0$以及投影变换矩阵，如何计算得到摄像机空间的$(vx,vy,vz)$顶点坐标。根据公式$(1)$，我们有：

$$(vx,vy,vz,1.0)=(projectMatrix)^{-1}\cdot clip \tag {2}$$

  而根据ndc顶点坐标$(nx,ny,nz)$与裁剪空间顶点坐标$clip$的关系，我们又有：

$$clip=(clip.xyz,clip.w)=((nx,ny,nz)\cdot clip.w, clip.w)=clip.w \cdot (nx,ny,nz,1.0) \tag {3}$$

  联立公式$(2)$与公式$(3)$，我们有：

$$(vx,vy,vz,1.0)=clip.w \cdot (projectMatrix)^{-1}\cdot (nx,ny,nz,1.0) \tag {4}$$

  公式$(4)$直接表明了摄像机空间顶点坐标与ndc空间坐标之间的关系，其中只有$clip.w$是未知，这是一个关键点。我们注意到$vw=1.0$，也就是在摄像机空间，顶点的分量为1.0。这一点可以利用起来：

$$clip.w\cdot[(projectMatrix)^{-1}\cdot (nx,ny,nz,1.0)].w = 1.0 \\ \to\\ clip.w=\frac{1.0}{[(projectMatrix)^{-1}\cdot (nx,ny,nz,1.0)].w} \tag {5}$$

  公式$(5)$意思就是$clip.w$等于ndc空间的坐标$(nx,ny,nz,1.0)$右乘逆投影矩阵所得向量的$w$分量的倒数。将其代入公式$(4)$中，我们可得：

$$(vx,vy,vz,1.0)=\frac{1.0}{[(projectMatrix)^{-1}\cdot (nx,ny,nz,1.0)].w} \cdot (projectMatrix)^{-1}\cdot (nx,ny,nz,1.0)$$

  因此，从ndc空间的坐标到摄像机空间的坐标，我们首先计算$(projectMatrix)^{-1}\cdot (nx,ny,nz,1.0)$，然后再将其$xyz$分量除以$w$分量即可。

vec3 uvToEye(vec2 coord, float z)
{
	vec2 pos = coord * 2.0f - 1.0f;
	vec4 clipPos = vec4(pos, z, 1.0f);
	vec4 viewPos = invProjectMatrix * clipPos;
	return viewPos.xyz / viewPos.w;
}

  知道了摄像机空间的顶点坐标，紧接着我们需要根据顶点坐标重建顶点法线。法线向量可以根据沿着x方向和沿着y方向的偏导数做叉乘得到，这里的x方向和y方向均为屏幕空间中的纹理坐标方向。求偏导数可以根据有限差分法：

$$\frac{\partial f}{\partial s}\approx\frac{f(s+\Delta s)-f(s)}{\Delta s} \tag {6}$$

  这里我们采用了单向差分法（前向差分法、后向差分法），没有采用中心差分法。为了避免计算出错误的法线向量，我们综合考虑前向差分法和后向差分法，取较小的那个差分值（差分值较大的很可能是在边界处与背景或距离比较远的流体深度值做了一个差分，这个时候得到的法线是错误的，因为深度值不连续）。我们对深度纹理图的周围四个像素分别做x方向和y方向的差分，$\Delta s=1$。最后根据得到的偏导向量做叉乘得到法线。

// -----------------reconstruct normal----------------------------
vec2 depthTexelSize = 1.0 / textureSize(depthTex, 0);
// calculate eye space position.
vec3 eyeSpacePos = uvToEye(Texcoord, depth);
// finite difference.
vec3 ddxLeft   = eyeSpacePos - uvToEye(Texcoord - vec2(depthTexelSize.x,0.0f),
				texture(depthTex, Texcoord - vec2(depthTexelSize.x,0.0f)).r);
vec3 ddxRight  = uvToEye(Texcoord + vec2(depthTexelSize.x,0.0f),
				texture(depthTex, Texcoord + vec2(depthTexelSize.x,0.0f)).r) - eyeSpacePos;
vec3 ddyTop    = uvToEye(Texcoord + vec2(0.0f,depthTexelSize.y),
				texture(depthTex, Texcoord + vec2(0.0f,depthTexelSize.y)).r) - eyeSpacePos;
vec3 ddyBottom = eyeSpacePos - uvToEye(Texcoord - vec2(0.0f,depthTexelSize.y),
				texture(depthTex, Texcoord - vec2(0.0f,depthTexelSize.y)).r);
vec3 dx = ddxLeft;
vec3 dy = ddyTop;
if(abs(ddxRight.z) < abs(ddxLeft.z))
	dx = ddxRight;
if(abs(ddyBottom.z) < abs(ddyTop.z))
	dy = ddyBottom;
vec3 normal = normalize(cross(dx, dy));
vec3 worldPos = (invViewMatrix * vec4(eyeSpacePos, 1.0f)).xyz;

  下图5显示了重建得到的法线情况，需要特别注意的是，这里我们重建得到的法线是在摄像机空间而非世界空间，这是因为我们还原的顶点也是摄像机空间的，因此计算光照时需要将光线向量变换到摄像机空间。

图5 重建的法线

  有了法线向量，接下来我们就计算水体折射、Blin-Phong光照。我这里只考虑水体折射，反射不考虑，因为一般清澈的水很少有反射现象。Beer-Lambert定律揭示了液体的光吸收现象。根据Beer-Lambert定律，液体的透光率随着液体的厚度增加呈指数衰减：

$$I(d)=I_0\cdot e^{-kd} \tag {7}$$

  公式$(7)$中，$d$是液体的厚度值，$I_0$是光照强度rgb向量，$k$是液体的光能衰减因子向量，通常等于$1.0-liquidColor$。液体的透光率计算如下所示，厚度值从之前渲染得到的贴图中直接采样得到。

float thickness = max(texture(thicknessTex, Texcoord).r, 0.3f);
vec3 transmission = exp(-(vec3(1.0f) - liquidColor.xyz) * thickness);

  然后，我们还需要从背景纹理图中采样，因为我们要实现折射的效果。为了实现折射的效果，我们需要对采样的纹理坐标做一个偏移，使之产生折射的效果。

float refractScale = 1.33 * 0.025;	// refracted index.
refractScale *= smoothstep(0.1, 0.4, worldPos.y);
vec2 refractCoord = Texcoord + normal.xy * refractScale;
vec3 refractedColor = texture(backgroundTex, refractCoord).xyz * transmission;

  最后就是关于Blin-Phong光照部分，比较简单，不再赘述。唯一需要注意的是我们获取的法线是在摄像机空间的，需要将光的方向也变换到摄像机空间。

// -----------------Phong lighting----------------------------
vec3 viewDir = -normalize(eyeSpacePos);
vec3 lightDir = normalize((viewMatrix * vec4(dirLight.direction, 0.0f)).xyz);
vec3 halfVec = normalize(viewDir + lightDir);
vec3 specular = vec3(dirLight.specular * pow(max(dot(halfVec, normal), 0.0f), 400.0f));
vec3 diffuse = liquidColor.xyz * max(dot(lightDir, normal), 0.0f) * dirLight.diffuse * liquidColor.w;

// -----------------Merge all effect----------------------------
fragColor.rgb = diffuse + specular + refractedColor;
fragColor.a = 1.0f;

  实现出来的效果如下图6所示。可以看到，渲染的效果很差，液体看起来像是由很多粒果冻组成，流体的粒子感非常明显，这并不是我们想要的。产生果冻壮流体的根本原因是因为我们的法线向量并不平滑，仔细观察图5，我们重建后的法线还是原来的球面上的法线，这造成光照效果的失真。

图6 实现的果冻壮流体

  因此，为了进一步提升渲染效果，我们要想办法使得流体表面得法线平滑。而法线来源于深度贴图，因为我们追溯到源头就是使得深度贴图尽可能地平滑。接下来我们将讨论在屏幕空间对深度贴图做的一些平滑后处理方案。

三、流体深度贴图的平滑处理

  我们现在需要对深度贴图做平滑处理，这其实属于图像处理的范畴。

1、采用高斯滤波平滑深度贴图

  首先是高斯模糊的平滑方案，我们把深度纹理当场一张图片，采用高斯权重做一个滤波操作。为了性能，同样我们将二维的高斯模糊分成水平方向和垂直方向两个pass。在之前实现辉光效果时已经介绍过，不再赘述。

	unsigned int DepthGaussianBlurFilter::blurTexture(unsigned int targetTexIndex, const glm::mat4 &projectMat)
	{
		m_framebuffer->bind();
		glDepthMask(GL_TRUE);
		glEnable(GL_DEPTH_TEST);
		glClear(GL_DEPTH_BUFFER_BIT);

		Shader::ptr blurShader = ShaderMgr::getSingleton()->getShader(m_blurShaderIndex);
		blurShader->bind();
		blurShader->setInt("image", 0);
		TextureMgr::getSingleton()->bindTexture(targetTexIndex, 0);
		
		for (unsigned int index = 0; index < 5; ++index) {
			// horizontal blur.
			blurShader->setInt("horizontal", 1);
			MeshMgr::getSingleton()->drawMesh(m_screenQuadIndex, false, 0);

			// copy to target texture.
			glCopyTexSubImage2D(GL_TEXTURE_2D, 0, 0, 0, 0, 0, m_width, m_height);

			// vertical blur.
			blurShader->setInt("horizontal", 0);
			MeshMgr::getSingleton()->drawMesh(m_screenQuadIndex, false, 0);

			// copy to target texture.
			glCopyTexSubImage2D(GL_TEXTURE_2D, 0, 0, 0, 0, 0, m_width, m_height);
		}

		TextureMgr::getSingleton()->unBindTexture(targetTexIndex);
		blurShader->unBind();
		m_framebuffer->unBind();
		return targetTexIndex;
	}

==============Fragment Shader==================
#version 330 core

in vec2 Texcoord;

uniform int horizontal;
uniform sampler2D image;

const float weight[8] = float[] (0.197448, 0.174697, 0.120999, 0.065602, 0.02784, 0.009246, 0.002403, 0.000489);

void main(){
	// gets size of single texel.
    vec2 tex_offset = 1.0 / textureSize(image, 0);
    float result = texture(image, Texcoord).r * weight[0];

	result += texture(image, Texcoord + vec2(tex_offset.x * 1 * horizontal, tex_offset.y * 1 * (1-horizontal))).r * weight[1];
    result += texture(image, Texcoord - vec2(tex_offset.x * 1 * horizontal, tex_offset.y * 1 * (1-horizontal))).r * weight[1];

	result += texture(image, Texcoord + vec2(tex_offset.x * 2 * horizontal, tex_offset.y * 2 * (1-horizontal))).r * weight[2];
    result += texture(image, Texcoord - vec2(tex_offset.x * 2 * horizontal, tex_offset.y * 2 * (1-horizontal))).r * weight[2];

	result += texture(image, Texcoord + vec2(tex_offset.x * 3 * horizontal, tex_offset.y * 3 * (1-horizontal))).r * weight[3];
    result += texture(image, Texcoord - vec2(tex_offset.x * 3 * horizontal, tex_offset.y * 3 * (1-horizontal))).r * weight[3];

	result += texture(image, Texcoord + vec2(tex_offset.x * 4 * horizontal, tex_offset.y * 4 * (1-horizontal))).r * weight[4];
    result += texture(image, Texcoord - vec2(tex_offset.x * 4 * horizontal, tex_offset.y * 4 * (1-horizontal))).r * weight[4];

	result += texture(image, Texcoord + vec2(tex_offset.x * 5 * horizontal, tex_offset.y * 5 * (1-horizontal))).r * weight[5];
    result += texture(image, Texcoord - vec2(tex_offset.x * 5 * horizontal, tex_offset.y * 5 * (1-horizontal))).r * weight[5];

	result += texture(image, Texcoord + vec2(tex_offset.x * 6 * horizontal, tex_offset.y * 6 * (1-horizontal))).r * weight[6];
    result += texture(image, Texcoord - vec2(tex_offset.x * 6 * horizontal, tex_offset.y * 6 * (1-horizontal))).r * weight[6];

	result += texture(image, Texcoord + vec2(tex_offset.x * 7 * horizontal, tex_offset.y * 7 * (1-horizontal))).r * weight[7];
    result += texture(image, Texcoord - vec2(tex_offset.x * 7 * horizontal, tex_offset.y * 7 * (1-horizontal))).r * weight[7];

	gl_FragDepth = result;
}

  经过高斯模糊之后的，重建得到的法线向量平滑了一下如下所示。

图7 高斯模糊平滑得到的法线

  然后用高斯模糊平滑得到法线向量做光照着色，得到下面的效果。渲染得到的效果看起来明显比图6的果冻壮好很多了。

图8 高斯模糊-光照着色

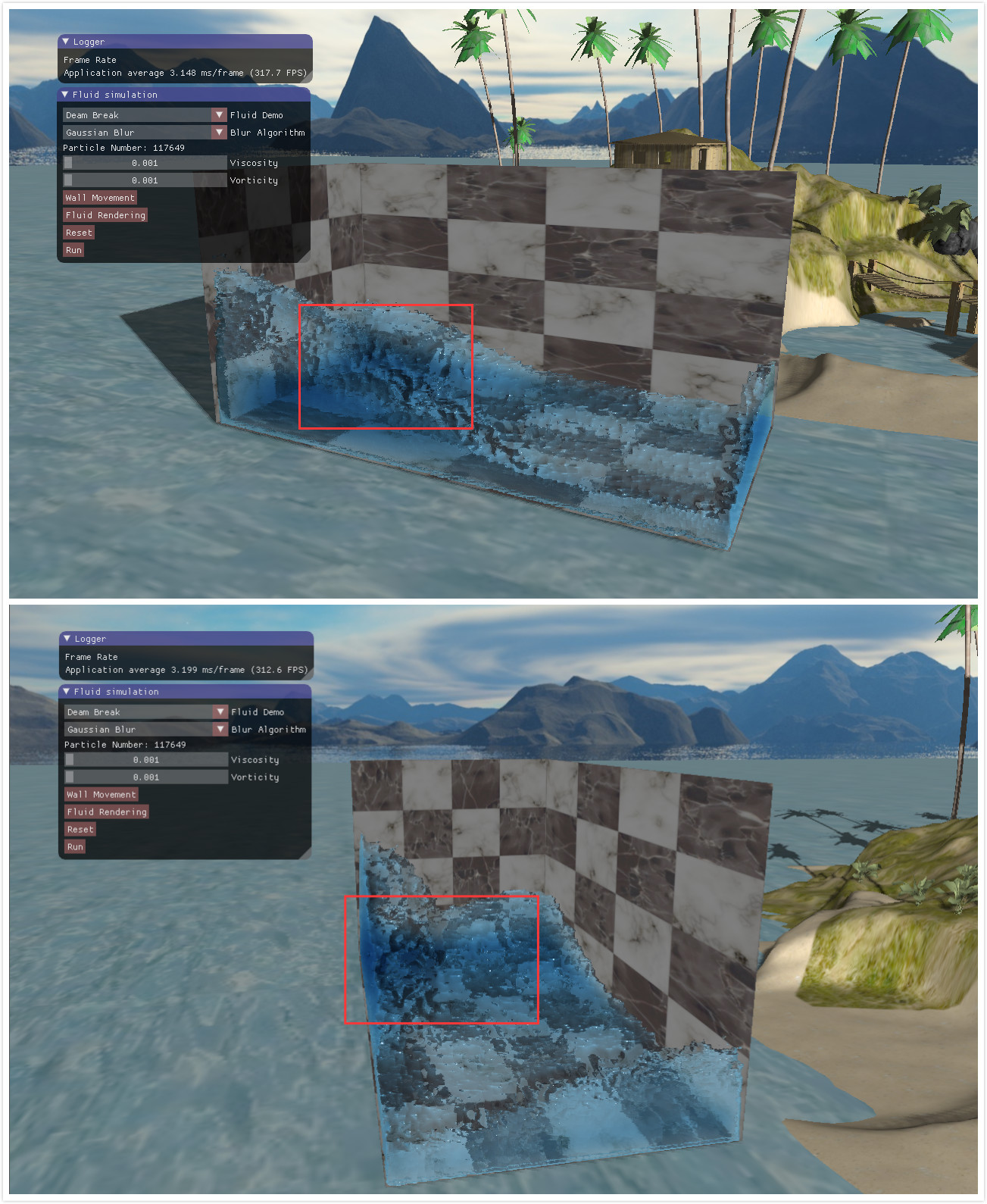
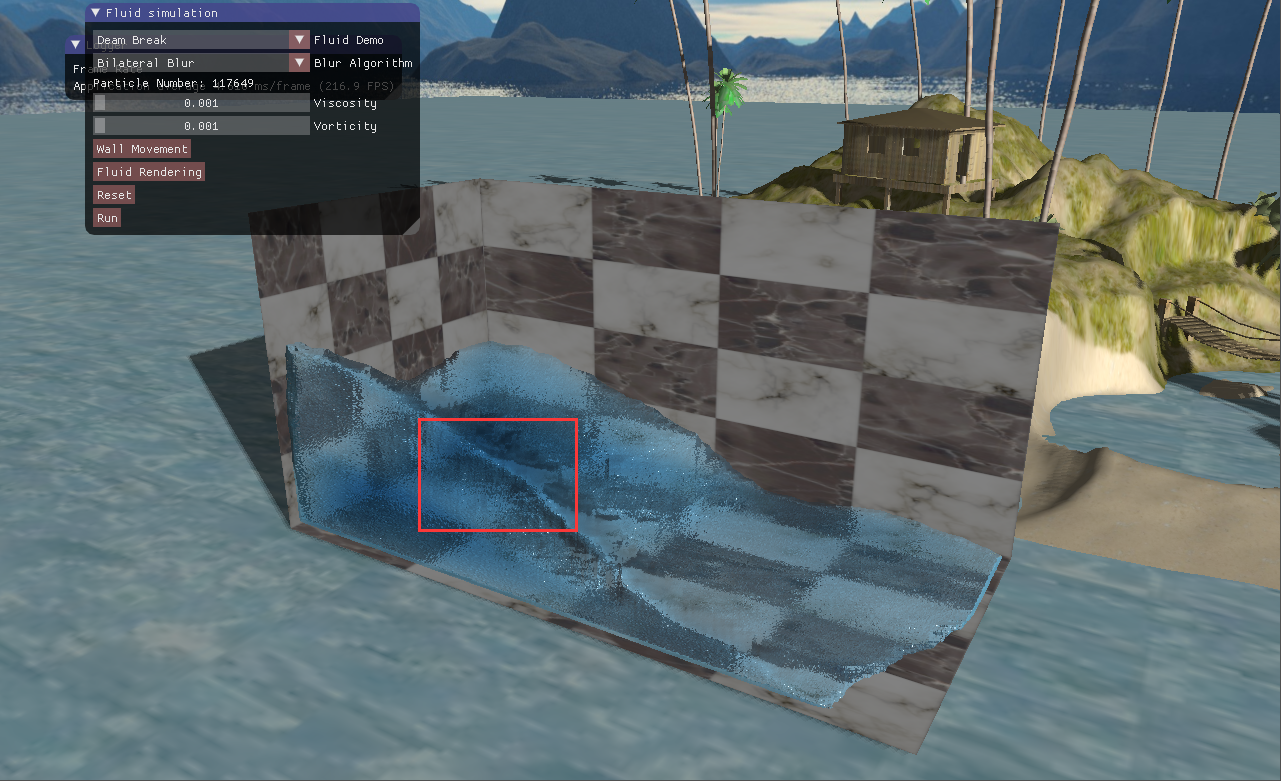
  然后高斯模糊的平滑方法存在一个问题，高斯模糊没有考虑深度值，它仅仅考虑当前像素到中心像素的距离。这就导致了高斯模糊会明显地模糊掉边界，使得边界与背景或较远处的流体看起来融合在一起了。如下图9所示，上面的这张图红框部分，流体的边界于后面的流体融合在了一起，看不出有一个边界在那里。下面这张图可以看到，流体是分开的，但是从上面的这个视角看起又是连在一起的。

图9 高斯滤波模糊掉了边界

3、采用双边滤波平滑深度贴图

  既然高斯模糊没有良好地保留边界，我们就选取一个能够保边去噪的滤波器，高斯双边滤波算法就是这样的一个滤波器。高斯模糊仅仅考虑了像素的空间分布，权重从中间向周边降低。而双边滤波则进一步考虑了图像的像素值，从而保证边缘部分不会被过滤掉。根据维基百科$^{[3]}$，一个双边滤波器定义为：

$$I^{filtered}(x)=\frac{1}{W_p}\Sigma_{x_i\in \Omega}I(x_i)f_r(||I(x_i)-I(x)||)g_s(||x_i-x||) \tag {8}$$

  其中，$I_{filtered}(x)$是过滤后的图像，$x$是被过滤的像素坐标，$\Omega$是像素$x$的滤波核领域，$I(x)$是初始未被过滤的图像。然后$f_r$是域值权重函数，$g_r$是空间权重函数。而$W_p$是归一化因子，其计算方式如下：

$$W_p=\Sigma_{x_i\in \Omega}f_r(||I(x_i)-I(x)||)g_s(||x_i-x||) \tag {9}$$

  可以看到$f_r$函数输入的是两个像素之间的差，而$g_s$输入的是两个像素坐标之间的差。考虑一个像素，其坐标为$(i,j)$，而其邻域像素的坐标为$(k,l)$，则计算与邻域像素$(k,l)$的滤波核函数为：

$$w(i,j,k,l)=exp(-\frac{(i-k)^2+(j-l)^2}{2\sigma_d^2}-\frac{||I(i,j)-I(k,l)||^2}{2\sigma_r^2}) \tag {10}$$

  公式$(10)$给出的核函数包含了$f_r$和$g_s$，其中左边部分就是$g_s$，而右边部分则为$f_r$。在片元着色器中，我实现的双边滤波函数如下所示。这是一个暴力的两重循环，因为图像的邻域是二维的。

#version 330 core

in vec2 Texcoord;

uniform sampler2D image;
uniform float filterRadius;

const float blurScale = 0.05f;
const float blurDepthFalloff = 500.0f;

void main(){
	// gets size of single texel.
    vec2 tex_offset = 1.0 / textureSize(image, 0);
	float sum = 0.0f;
	float wsum = 0.0f;
	float value = texture(image, Texcoord).r;
	for(float y = -filterRadius;y <= filterRadius;y += 1.0f)
	{
		for(float x = -filterRadius;x <= filterRadius;x += 1.0f)
		{
			float sample = texture(image, Texcoord + vec2(x, y) * tex_offset).r;
			// spatial domain.
			float r = length(vec2(x, y)) * blurScale;
			float w = exp(-r * r);
			// range domain.
			float r2 = (sample - value) * blurDepthFalloff;
			float g = exp(-r2 * r2);
			sum += sample * w * g;
			wsum += w * g;
		}
	}
	if(wsum >= 0.0f)
		sum /= wsum;
	gl_FragDepth = sum;
}

  然后根据双边滤波平滑后的深度图重建的法线如下图10所示。

图10 双边滤波平滑深度重建的法线

  由双边滤波平滑得到的法线做流体渲染如下图11，可以看到流体边界部分的保持得非常良好。

图11 双边滤波-保边良好

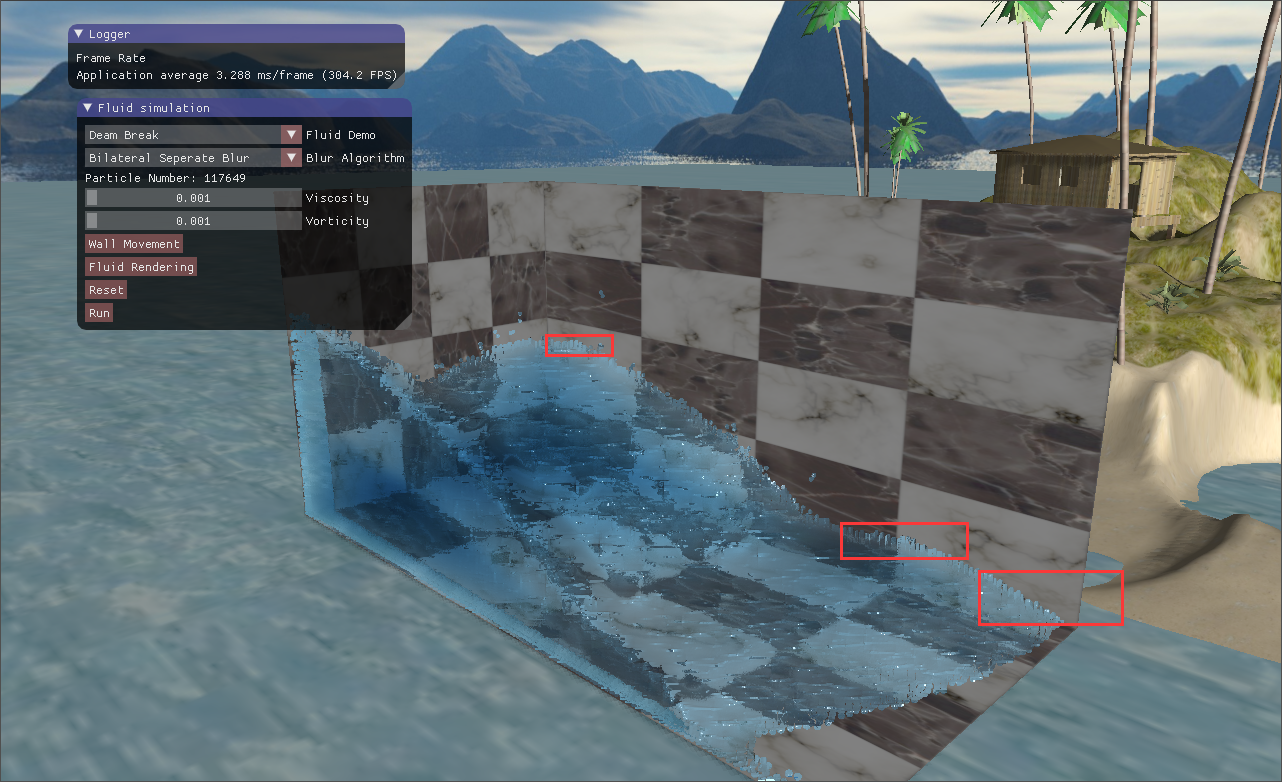
  但是这里又出现了一个性能方面的问题。双边滤波并不能像高斯模糊一样，拆分成水平方向依次、垂直方向一次，这是因为双边滤波考虑了图像的像素内容。一个核直径为20的双边滤波，每个像素要处理$20\times20=400$个邻域像素，这对于我的rtx2070显卡来说还好，但是在其他一些不那么好的显卡上会严重地拖慢渲染速度。Nvidia$^{[5]}$指出，可以强行将双边滤波分成两个pass，将$O(n^2)$的时间复杂度降到$O(n)$，一些失真可以勉强接受。然后我就尝试了将双边滤波分割成两个pass，水平方向和垂直方向各一次。效果如下图12所示，并不是非常好，在流体的一些边缘部分出现了拉伸的失真。

图12 双边分离滤波-边缘失真

4、采用曲率流平滑深度贴图

  由于双边滤波的不可分割性，Wladimir等人转向了另外一个不同的思路$^{[4]}$。我们的目标是寻转一个算法，能够平滑掉不同流体粒子之间的曲率突变，构建一个平滑、连续的流体表面。因此，一种思路就是最小化流体的曲率，这也跟流体的自然物理属性-流体表面张力相对应。我们称这个过程为曲率流（curvature flow）。

  曲率流沿着表面法线方向扩展，其速度取决于表面平均曲率。在我们的这个流体渲染中，我们仅仅处理的是流体表面的深度。在一帧当中，视角固定了，我们同样可以通过沿着曲率修改深度值达到平滑的效果：

$$\frac{\partial z}{\partial t} = H \tag {11}$$

  其中$t$是平滑时间步长，$z$就是我们的深度值，$H$就是流体表面的平均曲率，公式$(11)$意思是在每一次的平滑迭代中，深度值的变化梯度为流体表面的平均曲率。因此，我们首先要求流体表面的平均曲率，平均曲率的定义为表面单位法线的散度：

$$2H=\nabla\cdot \overline n \tag {12}$$

  给定屏幕空间的坐标以及深度值，视口宽高$V_x$、$V_y$，以及投影的x和y方向的焦距长（就是投影矩阵的mat[0][0]、mat[1][1]），我们得到摄像机空间顶点坐标与屏幕空间的x和y的关系：

$$P(x,y)= \left( \begin{matrix} \frac{\frac{2x}{V_x}-1.0}{F_x}\\ \frac{\frac{2y}{V_y}-1.0}{F_y}\\ 1.0 \end{matrix} \right)z(x,y) = \left( \begin{matrix} W_x\\ W_y\\ 1.0 \end{matrix} \right)z(x,y) \tag {13}$$

  然后法线向量由两个偏导叉乘得到：

$$n(x,y)=\frac{\partial P}{\partial x}\times \frac{\partial P}{\partial y} \\= \left( \begin{matrix} C_xz+W_x\frac{\partial z}{\partial x}\\ W_y\frac{\partial z}{\partial x}\\ \frac{\partial z}{\partial x} \end{matrix} \right) \times \left( \begin{matrix} W_x\frac{\partial z}{\partial y}\\ C_yz+W_y\frac{\partial z}{\partial y}\\ \frac{\partial z}{\partial y} \end{matrix} \right)\\ \approx \left( \begin{matrix} C_xz\\ 0\\ \frac{\partial z}{\partial x} \end{matrix} \right) \times \left( \begin{matrix} 0\\ C_yz\\ \frac{\partial z}{\partial y} \end{matrix} \right) = \left( \begin{matrix} -C_y\frac{\partial z}{\partial x}\\ -C_x\frac{\partial z}{\partial y}\\ C_xC_yz \end{matrix} \right)z \tag {14}$$

  其中$C_x=\frac{2}{V_xF_x}$，$C_y=\frac{2}{V_yF_y}$，公式$(14)$中我们忽略$W_x$和$W_y$是因为能够大大简化计算，且其贡献非常小。然后单位法线向量则为：

$$\overline n=\frac{n(x,y)}{|n(x,y)|}=\frac{(-C_y\frac{\partial z}{\partial x},-C_x\frac{\partial z}{\partial y},C_xC_yz)^T}{\sqrt{D}} \tag {15}$$ $$D=C_y^2(\frac{\partial z}{\partial x})^2+C_x^2(\frac{\partial z}{\partial y})^2+C_x^2C_y^2z^2 \tag {16}$$

  单位法线公式有了，现在回过头来看平均曲率的计算公式$(12)$，我们要求单位法线的散度。由于深度值z是关于屏幕空间坐标x和y的函数，因此$\frac{\partial \overline n}{\partial z}=0$，因为求偏导时x和y定为常数。故：

$$2H=\frac{\partial \overline n_x}{\partial x}+\frac{\partial \overline n_y}{\partial y} =\frac{C_yE_x+C_xE_y}{D^{\frac32}} \tag {17}$$ $$E_x=\frac12\frac{\partial z}{\partial x}\frac{\partial D}{\partial x}-\frac{\partial^2z}{\partial x^2}D \tag {18}$$ $$E_y=\frac12\frac{\partial z}{\partial y}\frac{\partial D}{\partial y}-\frac{\partial^2z}{\partial y^2}D \tag {19}$$

  求得了平均曲率之后，我们就根据公式$(11)$采用简单的欧拉差分法修改深度值。

#version 330 core

in vec2 Texcoord;

uniform float step;
uniform sampler2D image;
uniform mat4 projectMatrix;

void main(){
	float depth = texture(image, Texcoord).r;
	if(depth >= 1.0f || depth <= -1.0f)
	{
		gl_FragDepth = depth;
		return;
	}

	vec2 imageDim = textureSize(image, 0);
	vec2 texelSize = 1.0 / imageDim;
	
	// central differences.
	float depthRight = texture(image, Texcoord + vec2(texelSize.x, 0)).r;
	float depthLeft = texture(image, Texcoord - vec2(texelSize.x, 0)).r;
	float zdx = 0.5f * (depthRight - depthLeft);
	if(depthRight == 0.0f || depthLeft == 0.0f)
		zdx = 0.0f;
	
	float depthUp = texture(image, Texcoord + vec2(0, texelSize.y)).r;
	float depthDown = texture(image, Texcoord - vec2(0, texelSize.y)).r;
	float zdy = 0.5f * (depthUp - depthDown);
	if(depthUp == 0.0f || depthDown == 0.0f)
		zdy = 0.0f;

	float zdxx = depthRight + depthLeft - 2.0f * depth;
	float zdyy = depthUp + depthDown - 2.0f * depth;

	float depthFalloff = 0.00005f;
	if(abs(depth - depthRight) > depthFalloff || abs(depth - depthLeft) > depthFalloff)
		zdx = zdxx = 0.0f;
	if(abs(depth - depthDown) > depthFalloff || abs(depth - depthUp) > depthFalloff)
		zdy = zdyy = 0.0f;

	float Fx = projectMatrix[0][0];
	float Fy = projectMatrix[1][1];
	
	float Cx = -2.0f/(imageDim.x * Fx);
	float Cy = -2.0f/(imageDim.y * Fy);

	float D = Cy * Cy * zdx * zdx + Cx * Cx * zdy * zdy + Cx * Cx * Cy * Cy * depth;
	
	float Ex = 0.5f * zdx * dFdx(D) - zdxx * D;
	float Ey = 0.5f * zdy * dFdy(D) - zdyy * D;

	// curvature flow.
	float curvature = 0.5f * (Cy * Ex + Cx * Ey)/ pow(D, 1.5);
	if(curvature > 1.0f)
		curvature = 1.0f;

	gl_FragDepth = depth + curvature * step;
}

  然后在CPU端设置迭代多次，注意平滑的时间步长不能设置得太长。

unsigned int DepthCurvatureFlowBlurFilter::blurTexture(unsigned int targetTexIndex, const glm::mat4 &projectMat)
{
	m_framebuffer->bind();
	glDepthMask(GL_TRUE);
	glEnable(GL_DEPTH_TEST);
	glClear(GL_DEPTH_BUFFER_BIT);

	// blur.
	Shader::ptr blurShader = ShaderMgr::getSingleton()->getShader(m_blurShaderIndex);
	blurShader->bind();
	blurShader->setInt("image", 0);
	blurShader->setFloat("step", 0.00070f);
	blurShader->setMat4("projectMatrix", projectMat);
	TextureMgr::getSingleton()->bindTexture(targetTexIndex, 0);

	for (unsigned int iter = 0; iter < m_iterations; ++iter)
	{
		// blur.
		MeshMgr::getSingleton()->drawMesh(m_screenQuadIndex, false, 0);

		// copy to target texture.
		glCopyTexSubImage2D(GL_TEXTURE_2D, 0, 0, 0, 0, 0, m_width, m_height);
	}

	TextureMgr::getSingleton()->unBindTexture(targetTexIndex);
	blurShader->unBind();
	m_framebuffer->unBind();
	return targetTexIndex;
}

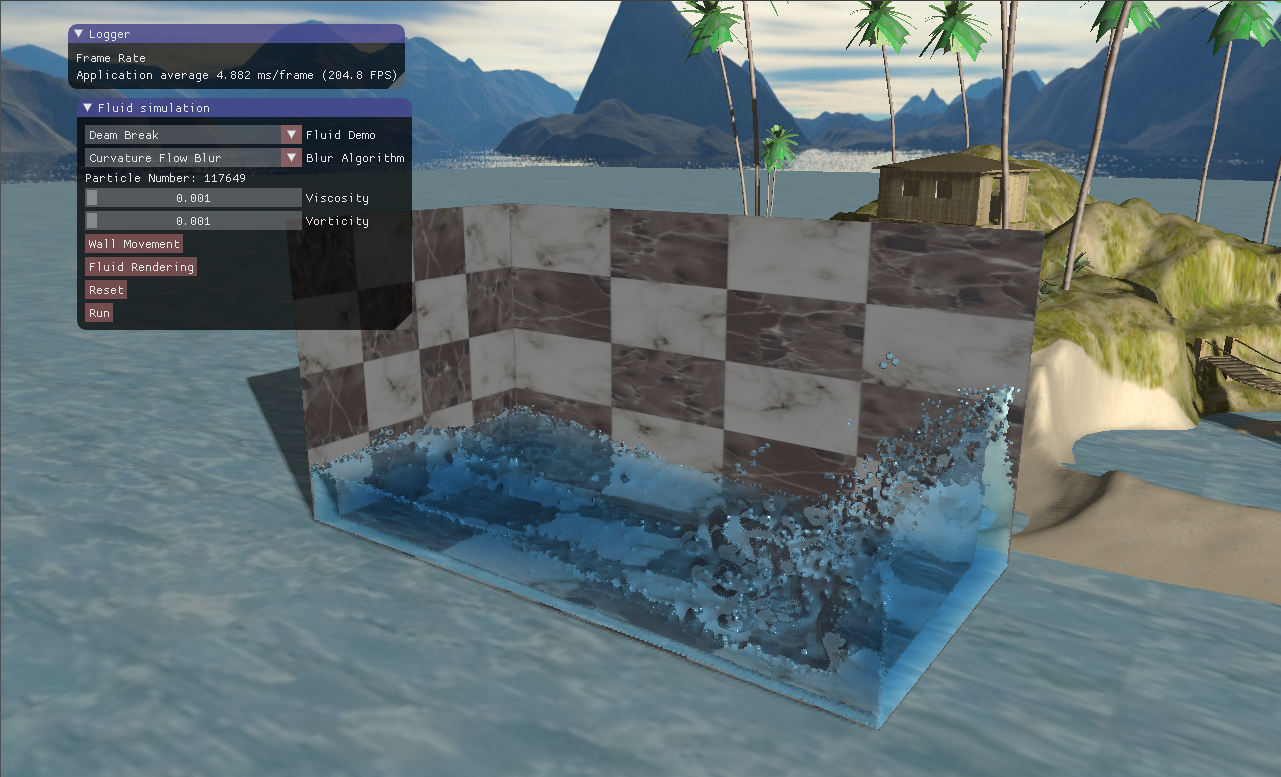
  然而采用曲率流得方法我实现的效果并不是想象中的那么好，总体上不如采用双边滤波的方法，颗粒感较强。而且不知道为什么，流体的表面有一些抖动，看起来很奇怪，大概这就是买家秀跟买家秀的区别吧。

图13 采用曲率流的平滑效果

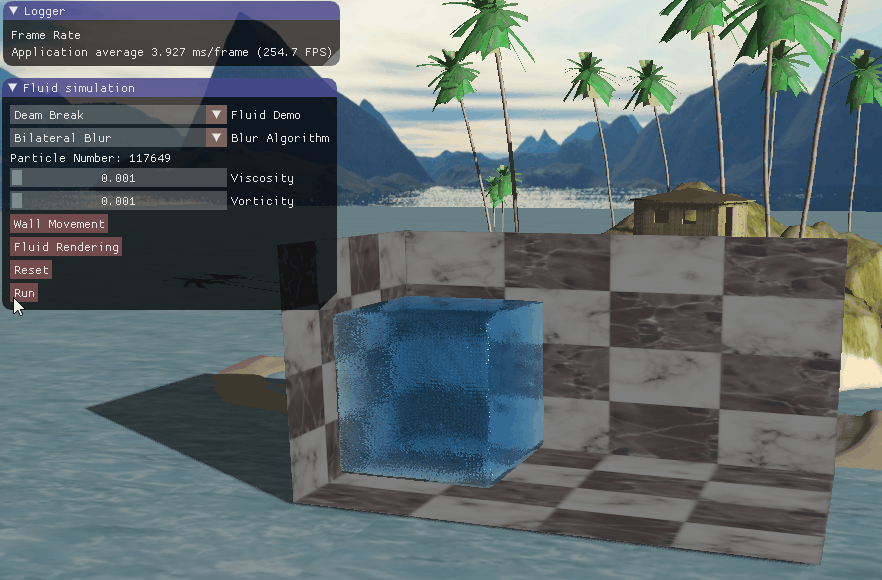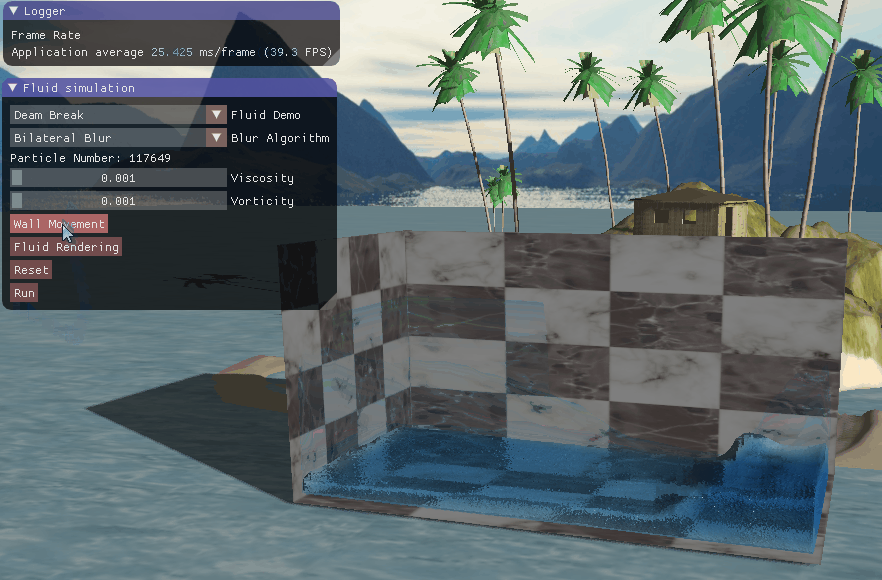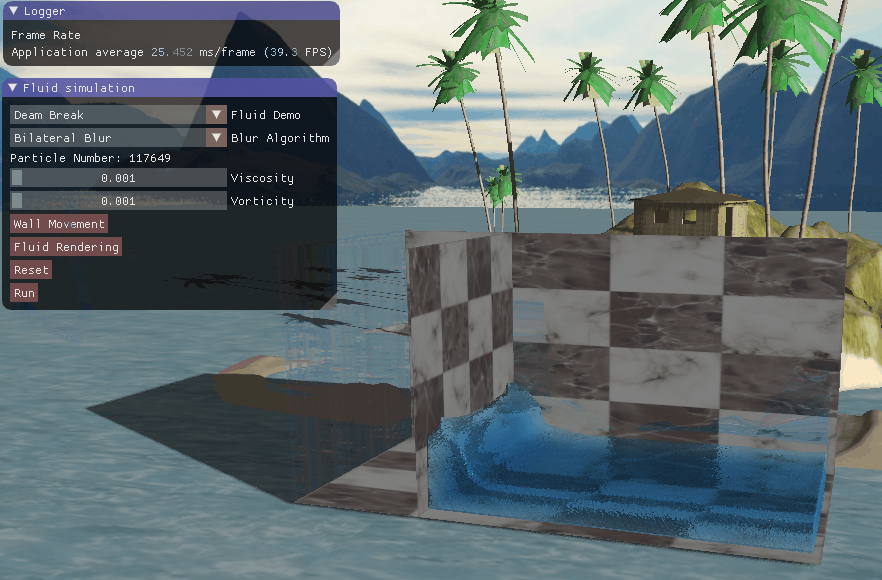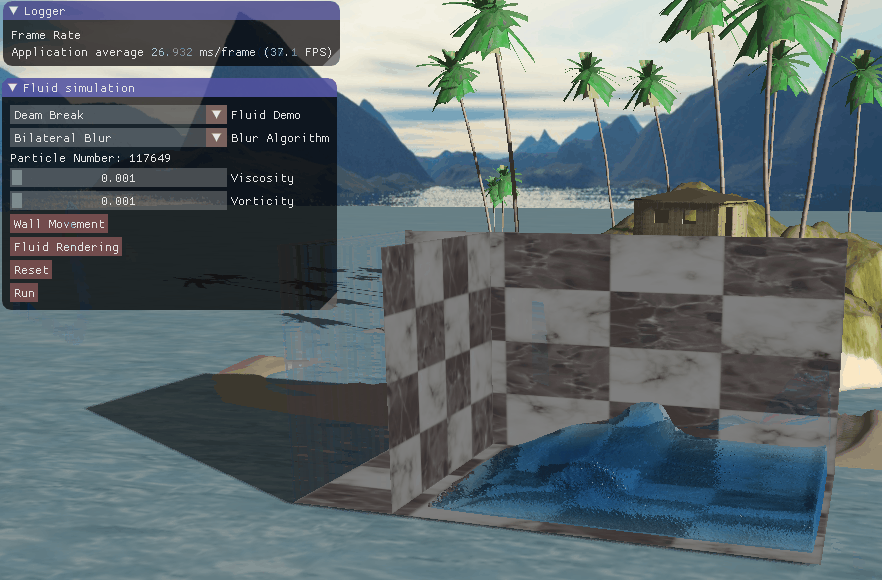
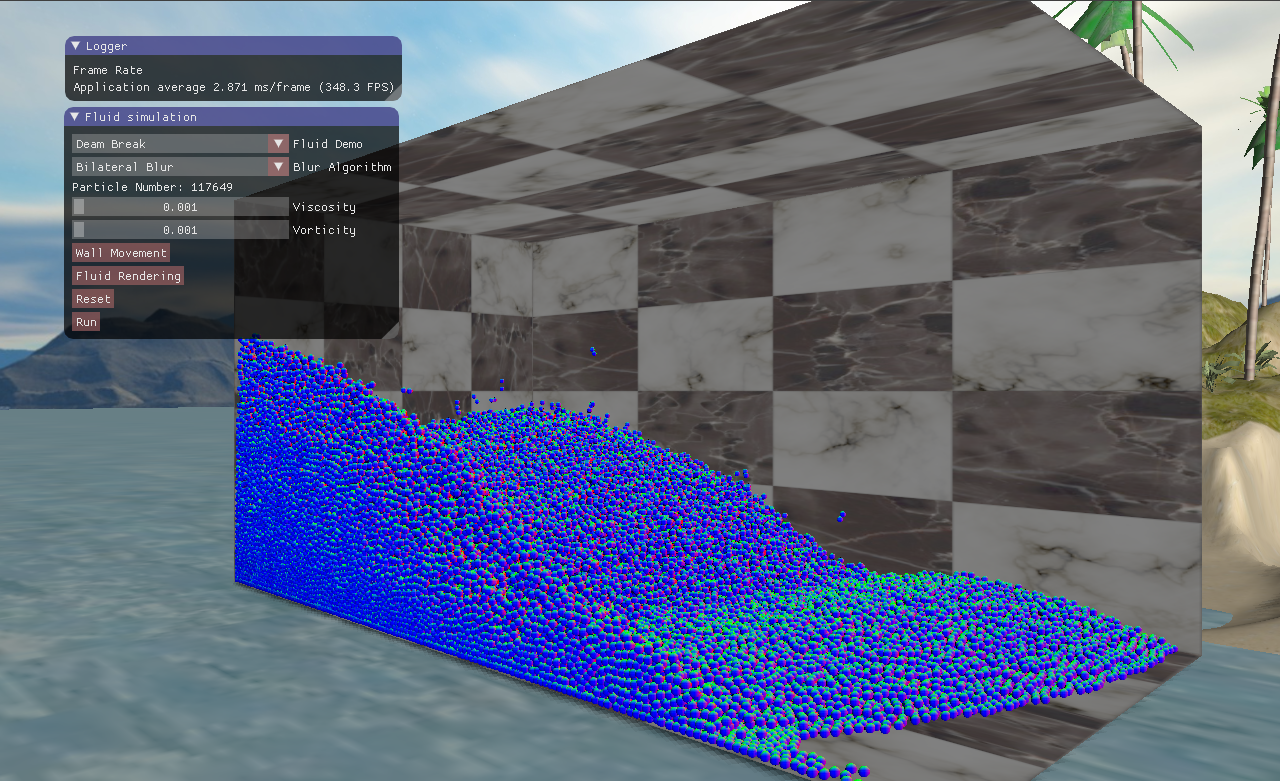
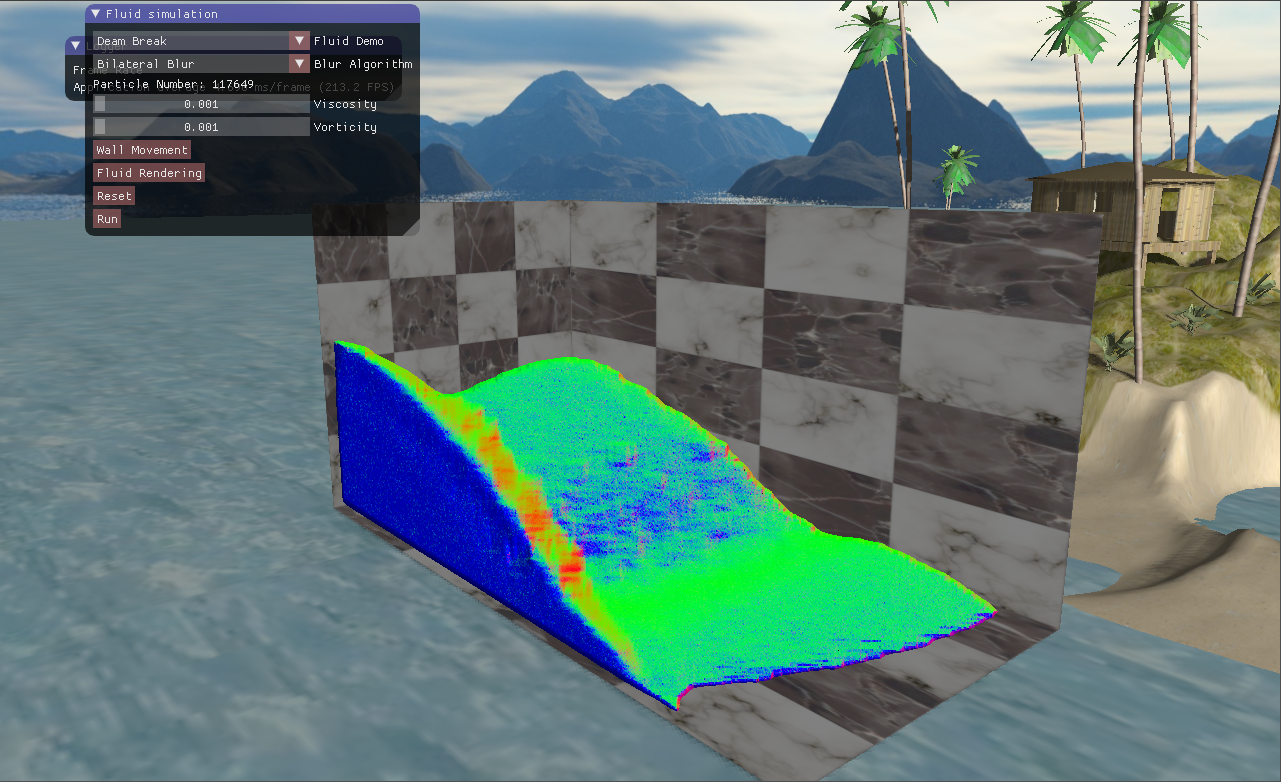
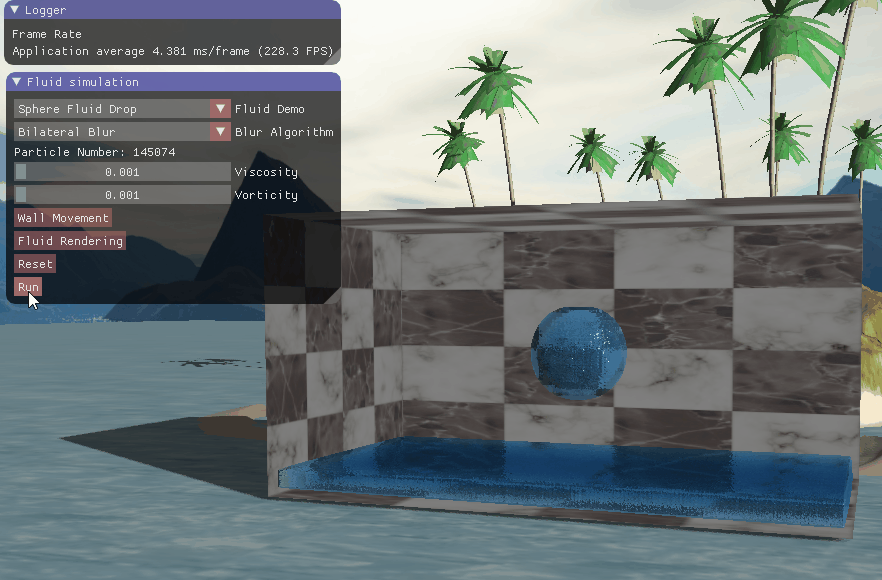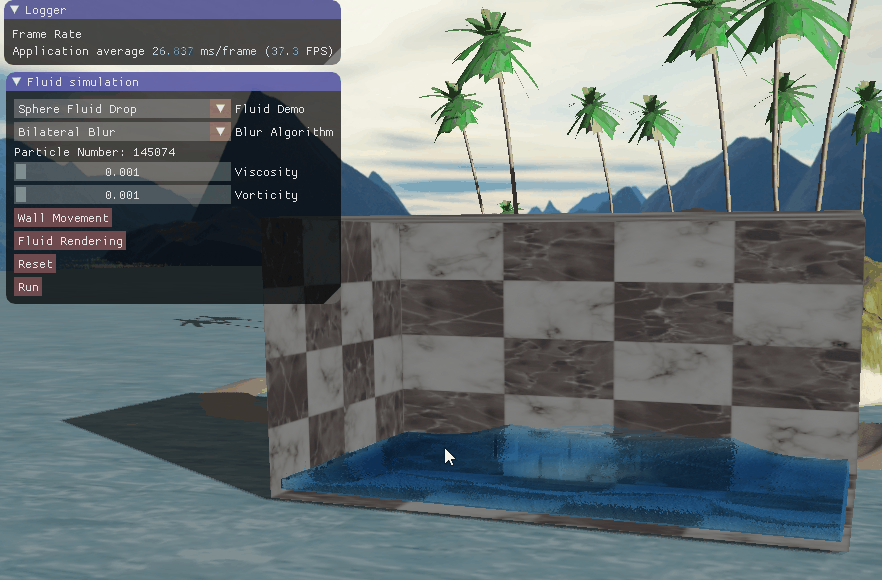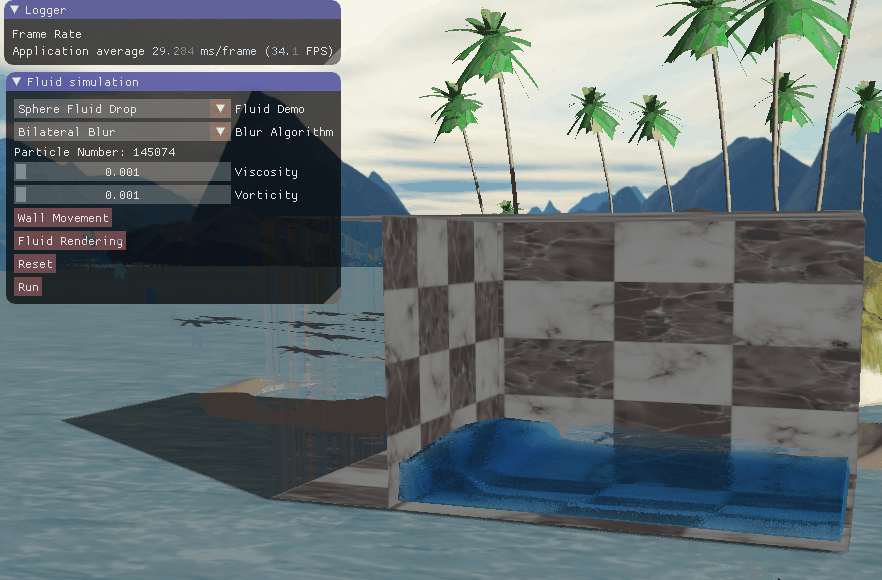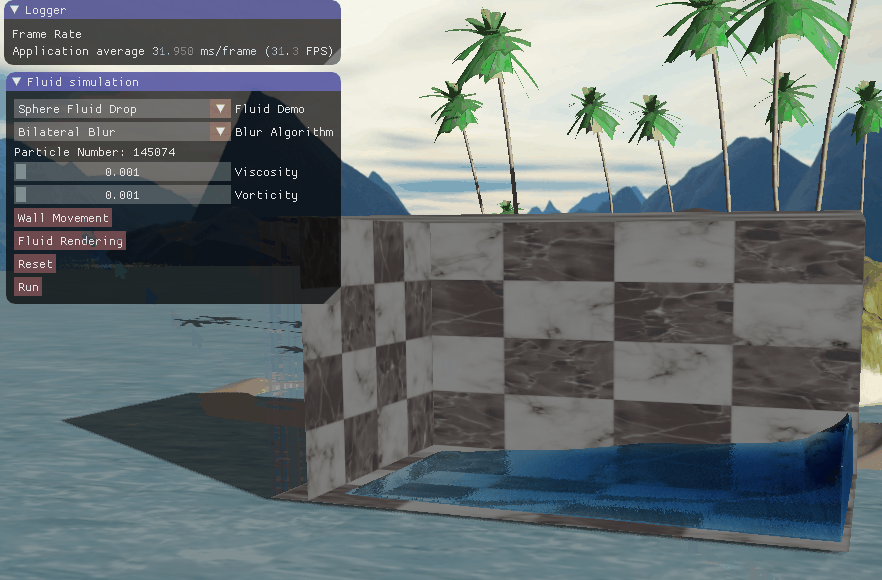
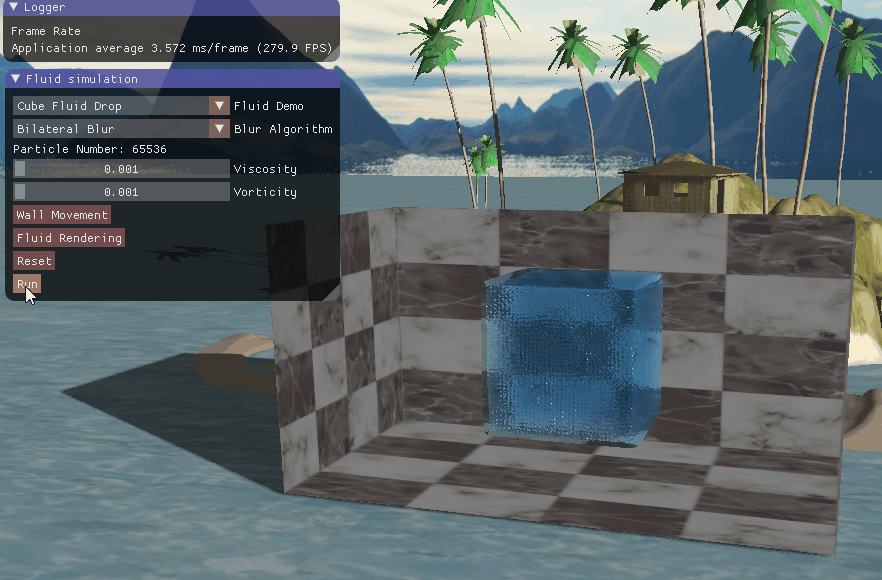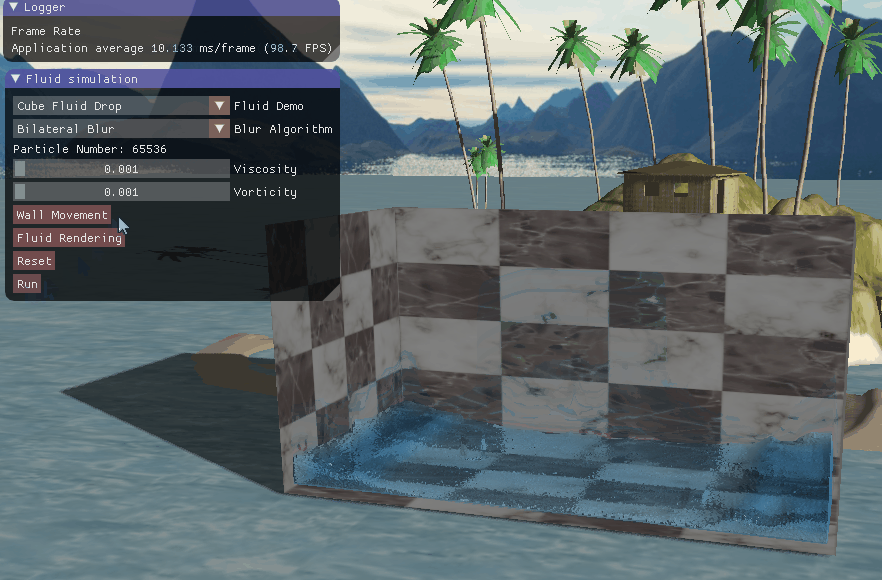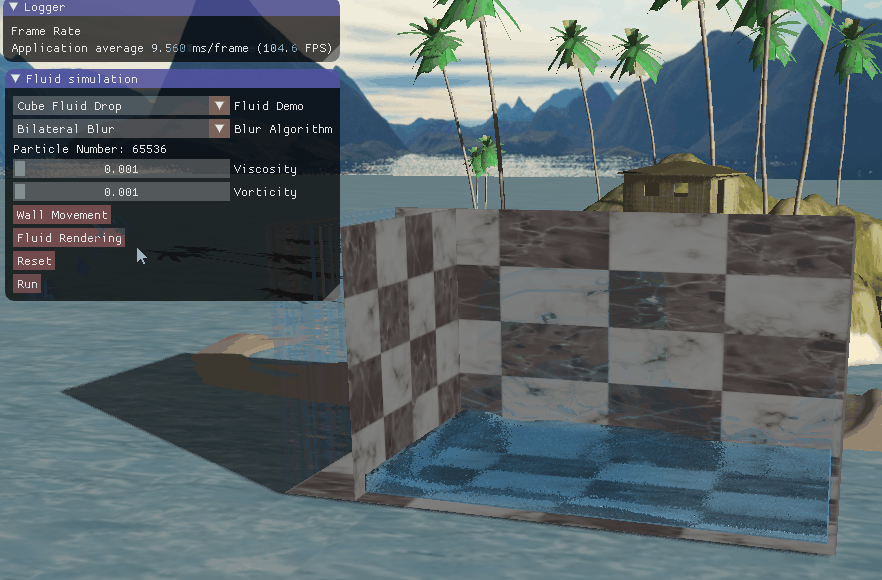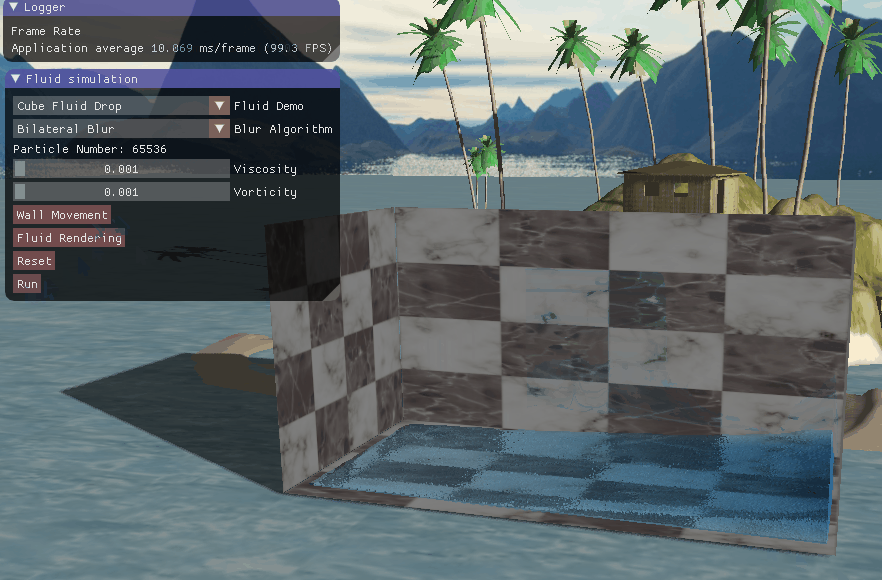
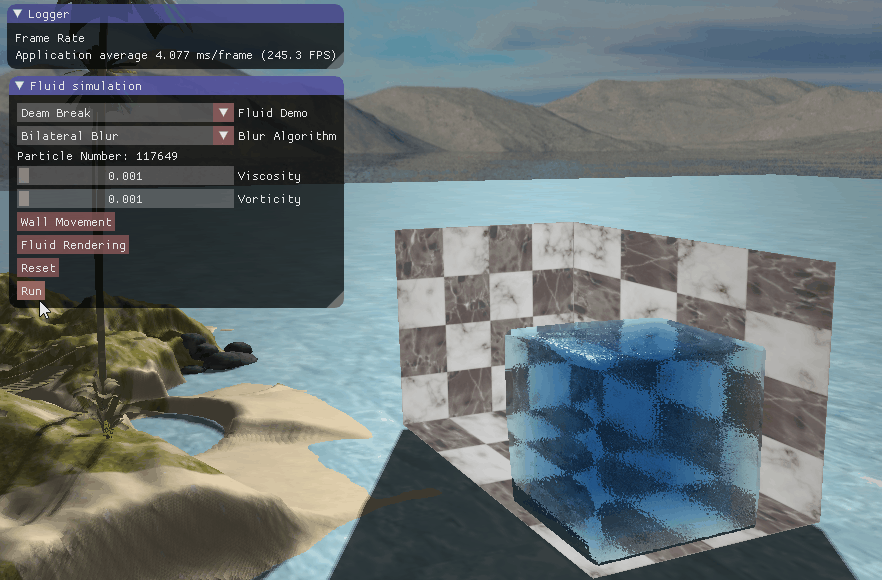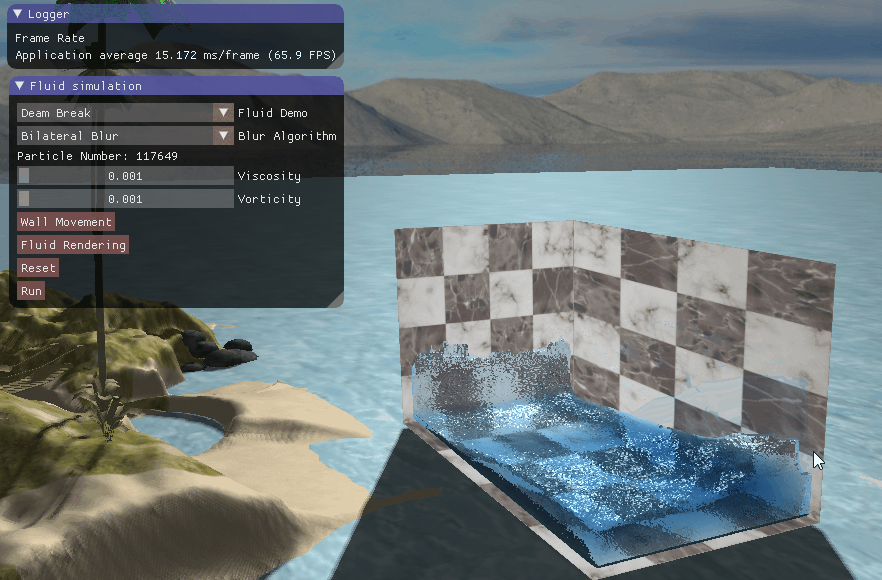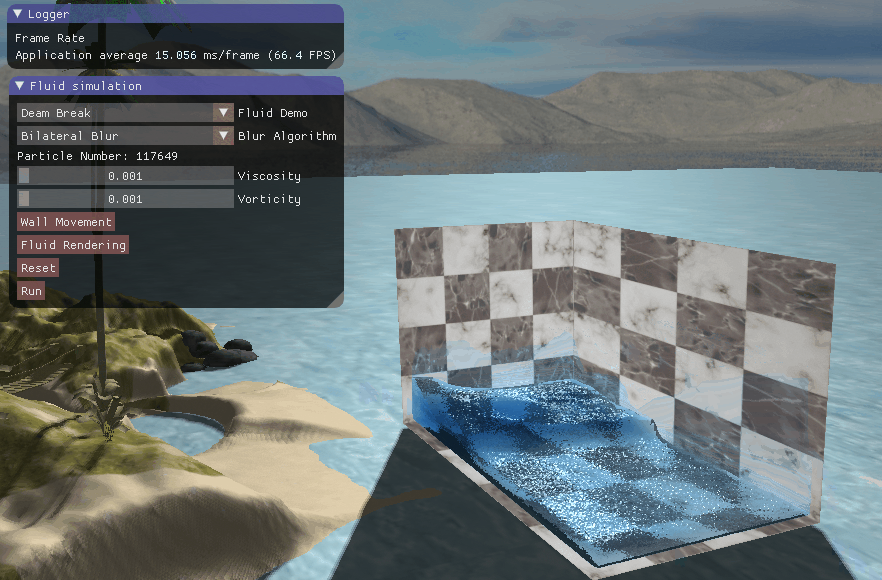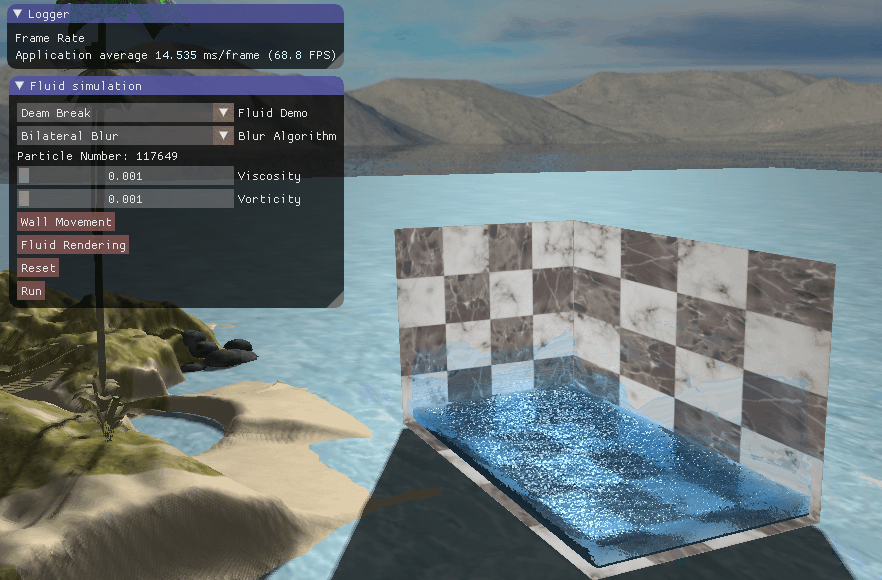
四、实现效果

参考资料：

$[1]$ How to go from device coordinates back to worldspace in OpenGL

$[2]$ W. E. Lorensen and H. E. Cline, “Marching cubes: A high resolution 3D surface construction algorithm,” in Proceedings of the 14th annual conference on Computer graphics and interactive techniques - SIGGRAPH ’87, 1987, pp. 163–169.

$[3]$ Bilateral filter. From Wikipedia, the free encyclopedia

$[4]$ W. J. van der Laan, S. Green, and M. Sainz, “Screen space fluid rendering with curvature flow” in Proceedings of the 2009 symposium on Interactive 3D graphics and games - I3D ’09, 2009, p. 91.

$[5]$ Screen Space Fluid Rendering for Games - Nvidia