N-body问题(或者说N体问题),是一个常见的物理模拟问题。在N-body系统中,每个粒子体都会与剩下的其他粒子产生交互作用(交互作用因具体问题而异),从而产生相应的物理现象。天体模拟就是一个非常经典的N-body系统,根据牛顿的万有引力定律,宇宙中的不同天体之间会产生相互作用的吸引力,吸引力根据两个天体之间的质量和距离的不同而各不相同,一个天体的运动轨迹最终取决于剩下的所有的天体对该天体的引力的合力。除了天体系统之外,N-body模拟在其他计算学科中也是常客。例如模拟蛋白质折叠现象就是通过计算N-body之间的静电和范德华力,**计算机图形学中的湍流流体的流动模拟和全局光照明计算都涉及到N-body问题的求解**。
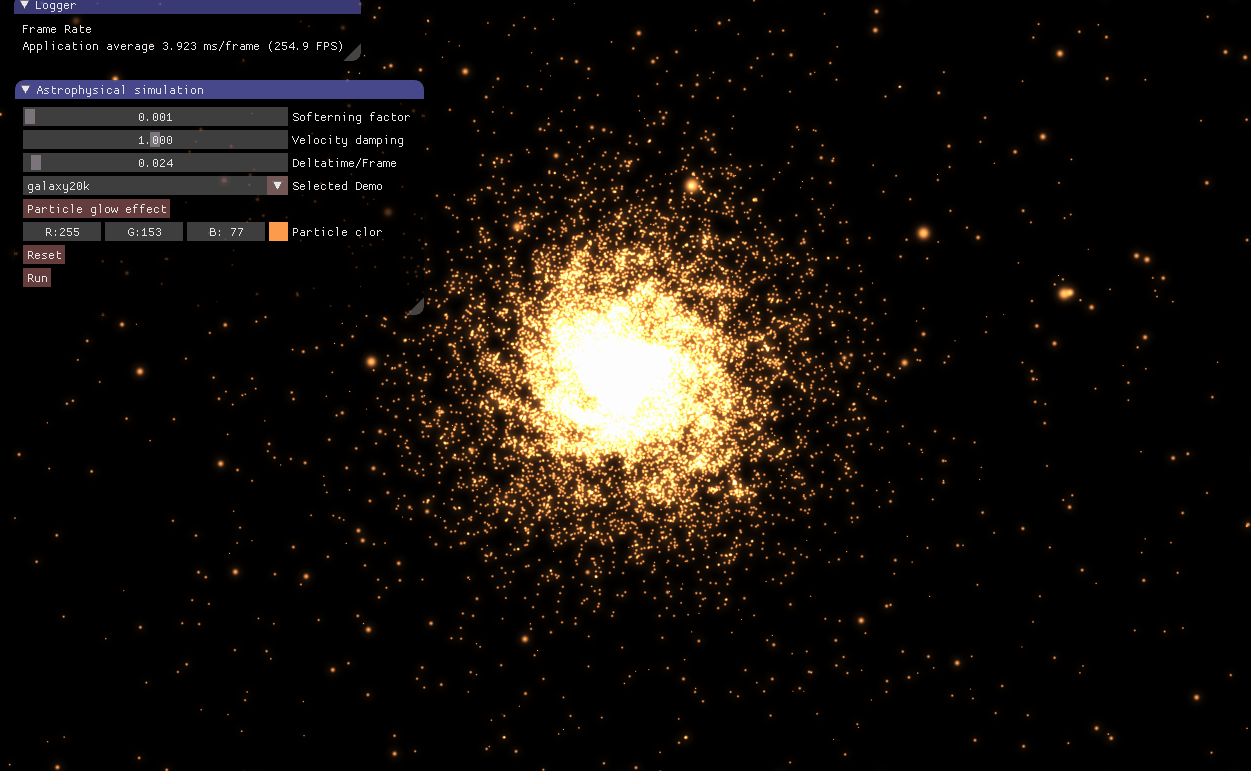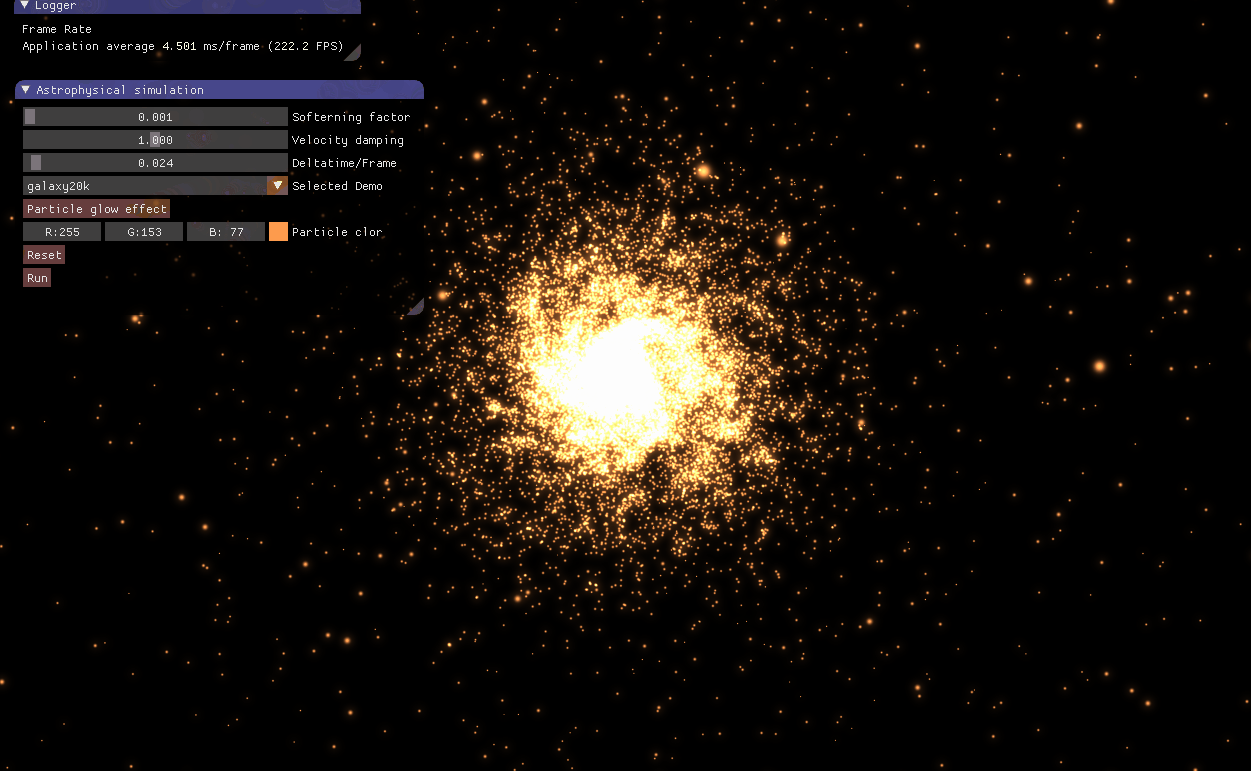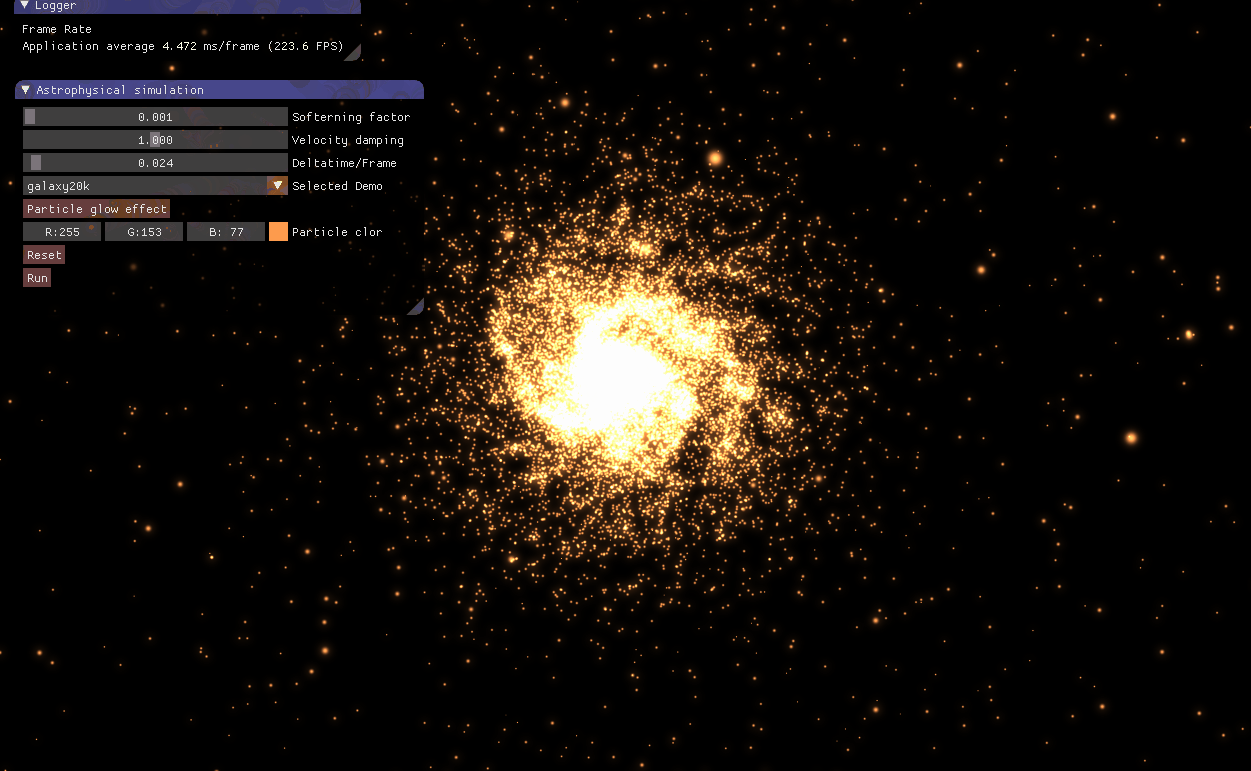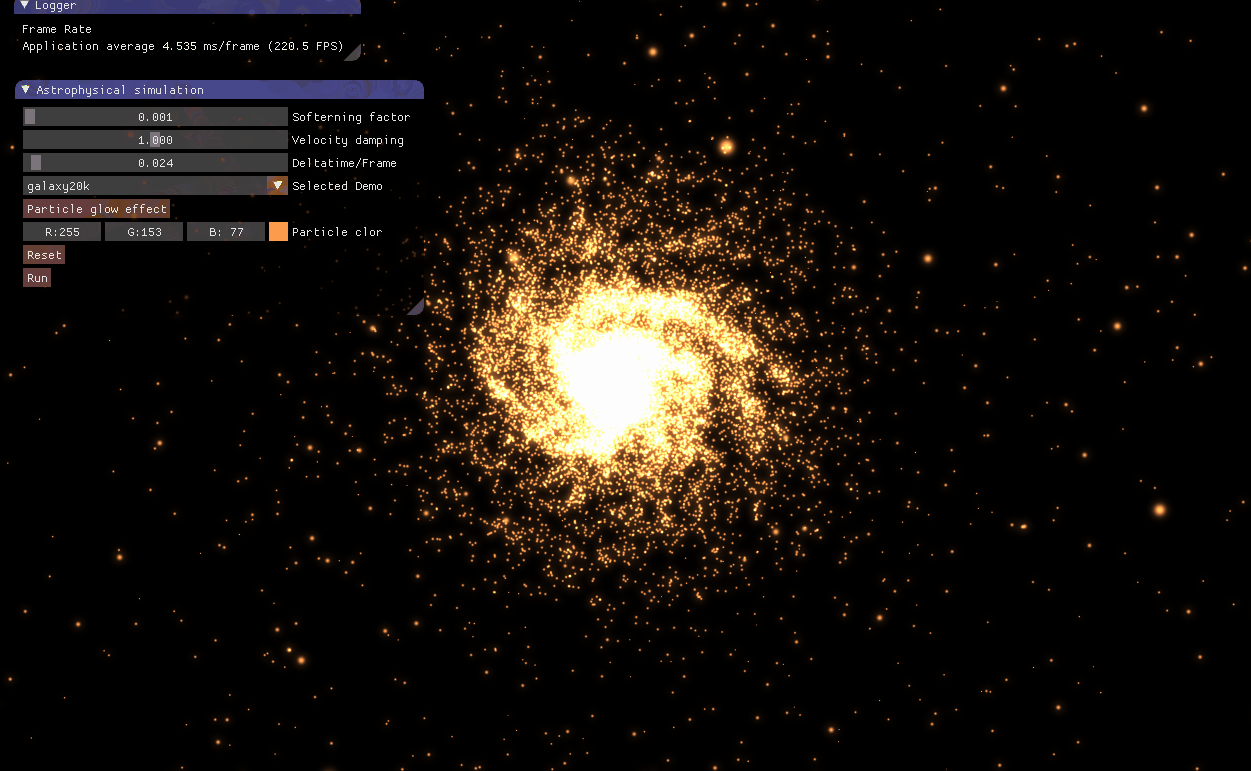
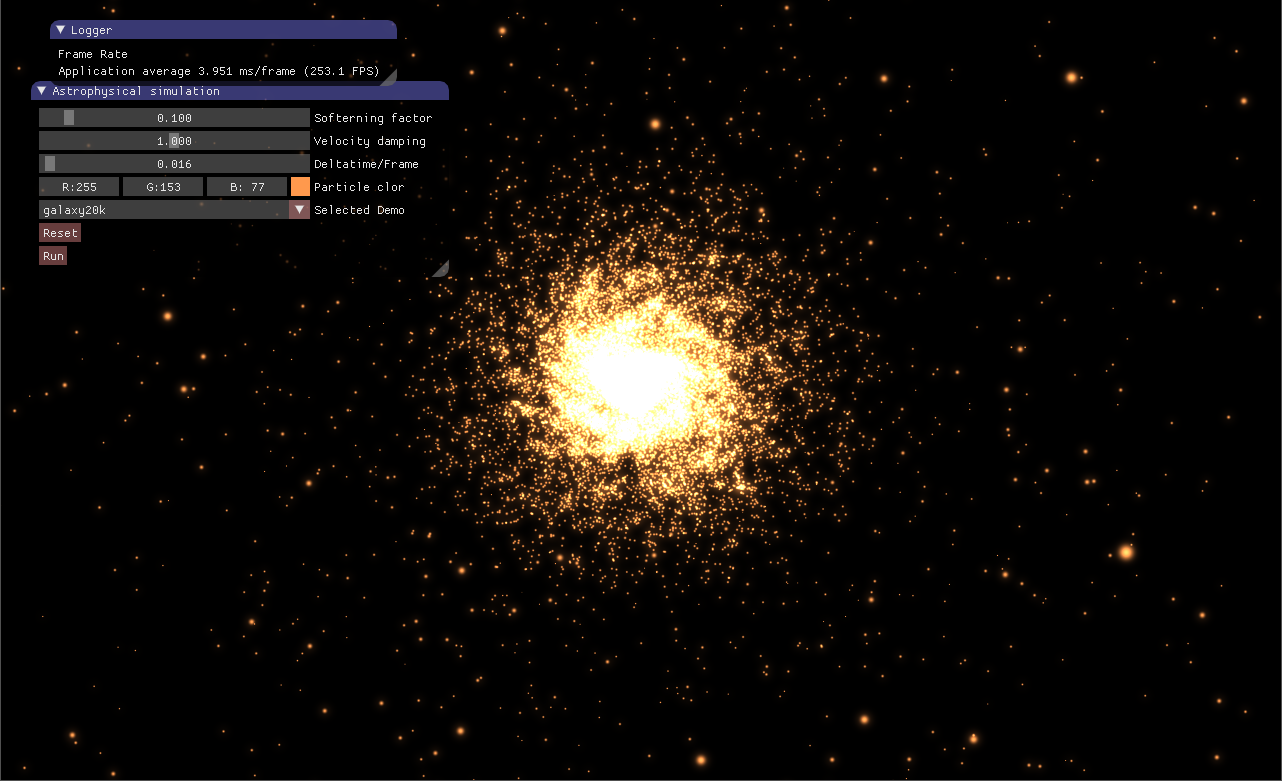
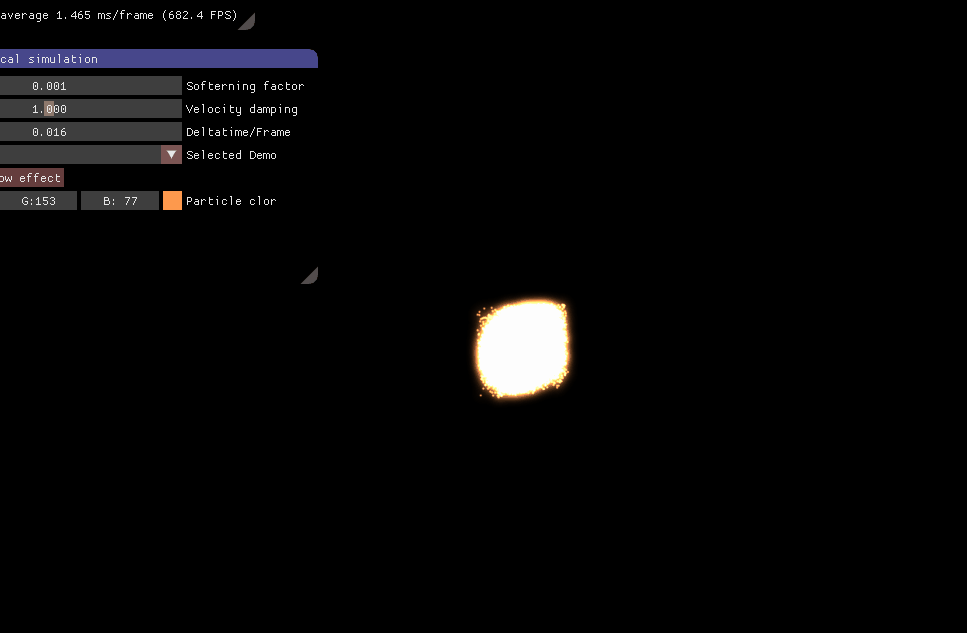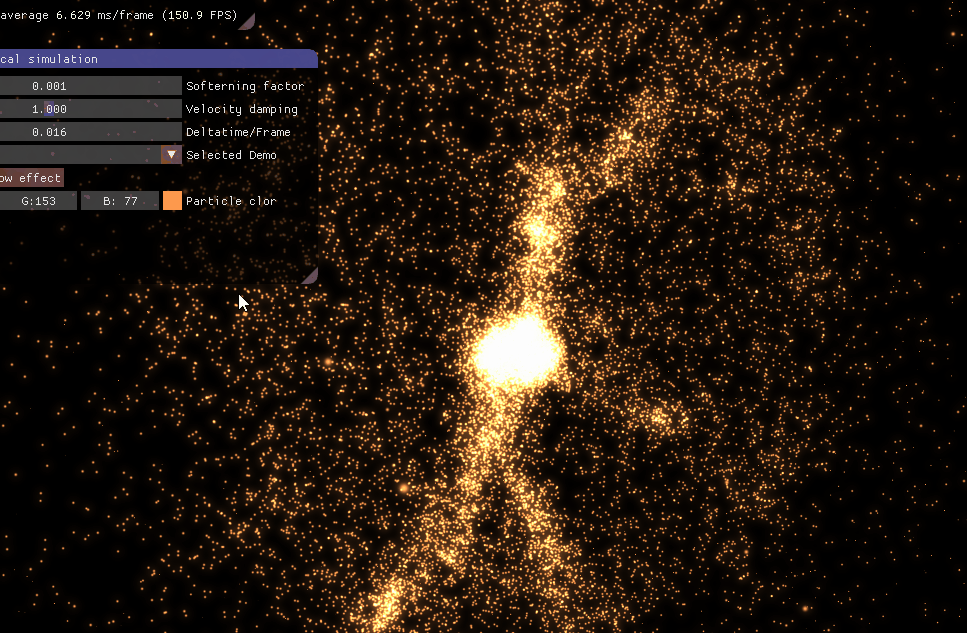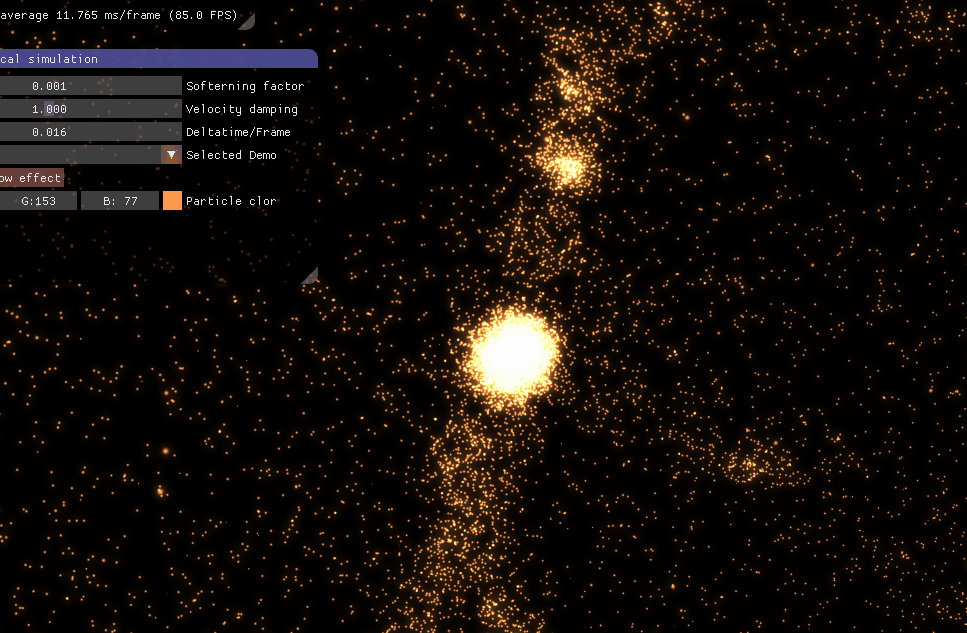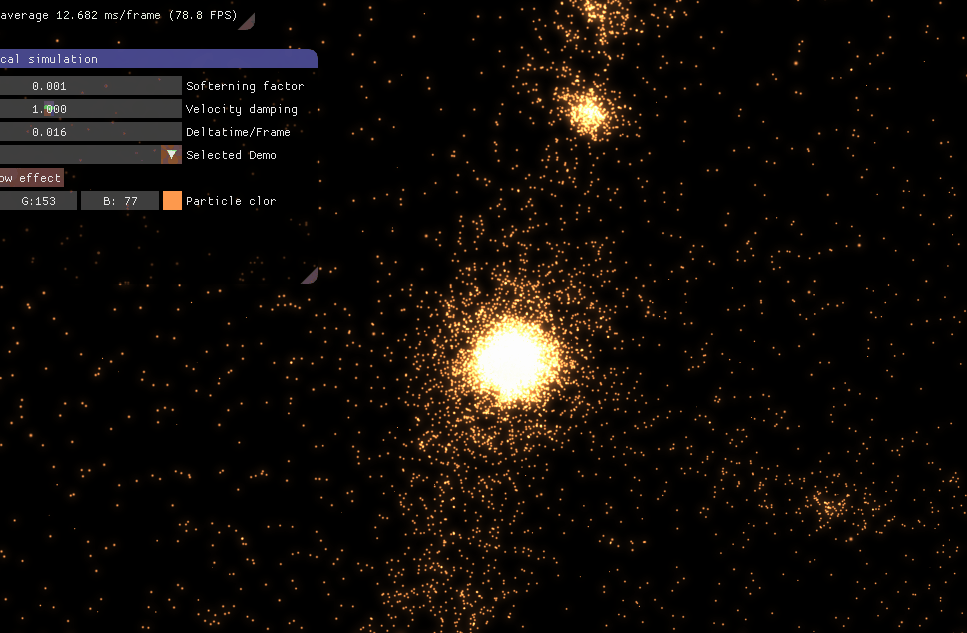
这周主要学习CUDA(全称为Computer Unified Device Architecture),它是一个NVIDIA的GPU编程模型,搞图形学不免常要与GPU打交道,所以非常有必要学习这个统一的GPU编程框架。N-body问题是计算机图形学中物理模拟的常见问题,在此我采用CUDA实现了一个天体星系的N-body模拟系统,充分利用GPU的并行能力去加速N-body的巨额计算过程。下面这张图就是我实现的天体星系模拟效果。
图1 天体星系的N-body模拟
1、天体的N-body系统 一种最简单的求解N-body的方法就是暴力法,被称为all-pairs法,它直接计算一个粒子体与剩下的所有粒子体的相互作用,对每一个粒子都做类似的处理,这样可以确保每个粒子体都与剩下的所有粒子体都产生交互作用,这种方法简单、暴力,但是算法的复杂度非常高,达到了$O(N^2)$量级,当模拟的N-body系统有$N=10000$个粒子时,算法就需要处理1亿次的相互作用计算。显然对于非常庞大的N-body系统,直接使用暴力法将非常耗时,因而通常不是简单地采用该算法。all-pairs法通常与一种基于长距离力的远场近似法结合,目前此类形式的算法包括Barnes-Hut法$^{[1]}$、快速多极法$^{[2]}$和粒子网格法$^{[3]}$等等。
上面提到的几种加速方法最耗时的部分依旧是all-pairs部分,因此这是一个非常关键的部分,如果能够加速这一部分,那么模拟的速度将大大提升。因此,目前我们只关注all-pairs算法部分,而且不是在CPU上实现该算法的串行,而是接用CUDA编程模型实行一个GPU并行的快速版本。接下来先介绍一下天体星系的N-body系统。
天体星系模拟主要考虑的是万有引力。给定$N$个天体,我们记每个天体$0\leq i<N$的位置向量为$x_i$、速度向量为$v_i$、质量为$m_i$,根据牛顿的万有引力定律,任意两个不同天体$i$和$j$之间的万有引力计算公式如下所示:
公式$(1)$中的$r_{ij}=x_j-x_i$为从天体$i$到$j$的一个方向向量,故其模长为两者之间的距离。$G$是万有引力常数。上面这个公式可能看起来跟我们高中时学的万有引力公式略有不同,这是因为高中时还没有将力是一个矢量这个概念显示地表达出来,公式$(1)$中的$\frac{r_{ij}}{||r_{ij}||}$是一个从$i$到$j$的单位方向向量。上述公式描述的是天体$j$对天体$i$的引力,那么除$i$之外的所有天体对天体$i$的引力合力的计算公式为:
公式$(2)$有个潜在的不稳定问题,当两个粒子之间的距离向量$r_{ij}\to0$时,$||r_{ij}||$取值为$0$,从而导致除零错误,在计算机系统中这将导致程序崩溃。因此,为了避免这种情况,我们在公式$(2)$的基础上给它的分母再加上一个软化因子(softening factor)$ε^2>0$,从而万有引力近似计算公式为:
公式$(3)$中,当$ε$取0时,就是原来的公式$(2)$。除此之外,注意公式$(3)$中还去掉了公式$(2)$中的条件判断$i\neq j$,这样带来的另外一个好处就是免去了条件判断语句,这对GPU非常友好,因为GPU擅长的是算术运算,逻辑运算会或多或少地拖慢GPU的并行速度。根据公式$(3)$我们现在得到了某一个天体的引力合力,我们还要根据这个合力计算天体的加速度,接着根据加速度计算天体的速度,最后得到天体的位置向量。由牛顿定律可知,天体加速度$a_i=F_i/m_i$,结合公式$(3)$消去$m_i$,我们可得下面的加速度计算公式$(4)$:
对于天体的N-body模拟,我们实际上要计算的就是公式$(4)$。
2、基于CUDA的N-body实现 N-body模拟的all-pairs算法复杂度为$O(N^2)$,这是相对于串行来说的,但是在GPU上我们可以通过并行来消减算法所需的时间,即通过空间上的并行来降低时间上的复杂度。我们要在CUDA上解决一个问题,首先要分析问题,发现该问题潜在的并行性。对于一个天体系统,我们通过分析发现任两个天体$i$和$j$之间的万有引力$f_{ij}$计算不涉及到其他天体的计算结果,即计算是独立的。$N$个天体的星系需要计算的就是$N\times N$大小的矩阵,第$i$行、$j$列的矩阵项为$f_{ij}$。所以一个非常自然的想法就是,通过并行计算每个矩阵项$f_{ij}$,这样看起来理论上花费的时间就是计算一个矩阵项$f_{ij}$的时间,算法的复杂度降为$O(1)$。但是在GPU上实现并行算法时,我们还要考虑内存访问的时间。上面我们提到的想法需要耗费$O(N^2)$量级的内存空间,这是一个非常大的空间复杂度,很可能我们的显卡上并没有这么大的显存,除此之外显存的访问也将明显拖慢我们的并行速度。
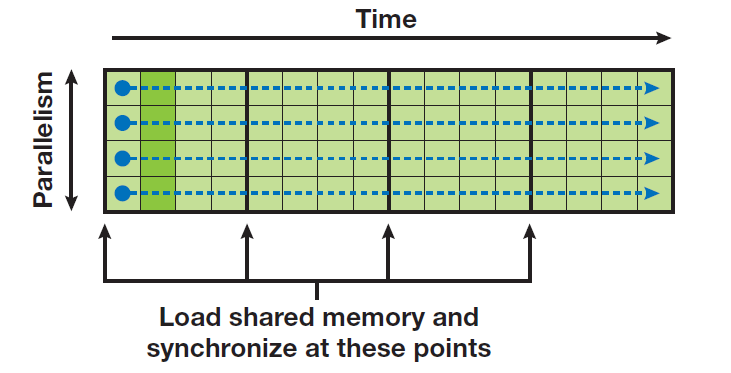
因此,为了同时考虑时间和空间的开销,我们需要在两者之间做一个平衡。一个非常不错的做法就是给时间和空间各自分配一个$O(N)$的复杂度,相对于$O(N^2)$,$O(N)$是一个极大的算法复杂度提升。我们知道,对于每一个天体,都要遍历$N$个天体计算加速度。因此,我们采用这样的一个策略:对于每个天体,我们串行地计算它的加速度,不同天体之间的加速度并行计算。这个策略不难理解,如下图2所示,横向是时间轴、纵向是空间轴,在时间轴方向上,每个天体的加速度串行计算;在空间轴方向上,不同天体之间独立地并行。
图2 GPU上纵向并行、横向加速
接下来就考虑如何在CUDA上实现该策略。首先是每一对天体之间引力的加速度计算,我们直接套用前面提到的公式即可,这里需要注意距离向量的计算。因为万有引力是吸引力,因此天体$j$对天体$i$的引力方向是从$i$到$j$的。CUDA的kernel代码如下所示,可以看到一对天体之间的引力计算需要耗费20次的浮点数运算。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 __device__ float3 bodyPairInteraction (float4 pi, float4 pj, float3 ai) float3 distVector = { 0.0f , 0.0f , 0.0f }; distVector.x = pj.x - pi.x; distVector.y = pj.y - pi.y; distVector.z = pj.z - pi.z; float distSquared = distVector.x * distVector.x + distVector.y * distVector.y + distVector.z * distVector.z; distSquared += getSofteningSquared(); float invDist = rsqrtf(distSquared); float invDistCubic = invDist * invDist * invDist; float coff = pj.w * invDistCubic; ai.x += distVector.x * coff; ai.y += distVector.y * coff; ai.z += distVector.z * coff; return ai; }
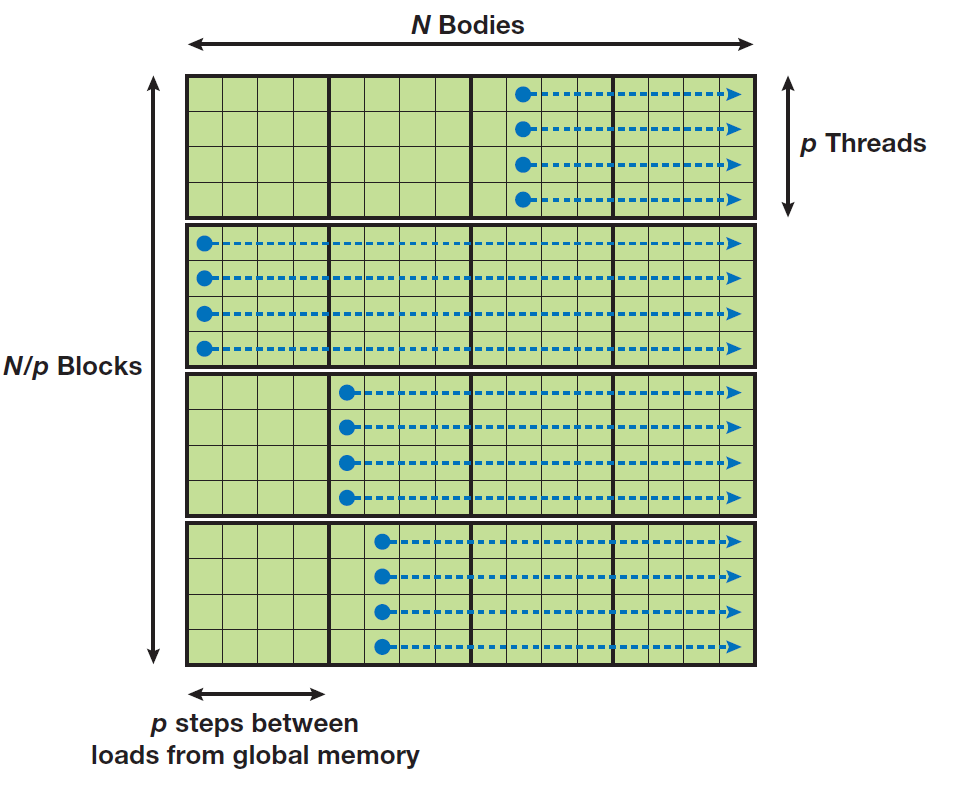
一个天体占据一个GPU线程,串行地调用上面的bodyPairInteraction函数。这里我们需要考虑内存的访问。CUDA的内存分为三大类:全局内存、共享内存、寄存器内存,访问速度从左到右越来快。寄存器内存就是单个线程占据的局部内存,这里我们仅仅考虑全局内存和共享内存。全局内存的访问速度非常慢,为了性能我们必须考虑这一点。共享内存仅限于同一个线程块内,不同线程块之间的线程没有共享内存这一概念。既然共享内存仅限于同一个线程块,我们就采用一个分块的策略,不同天体计算各自的加速度之间是有数据重用的,先将天体数据预先加载到共享内存,同一个线程块的线程访问这个共享内存做相应的数值计算。但是又引入一个问题,共享内存是有限的,所以对于一个线程块的共享内存,我们不是一次性地将所有天体数据从全局内存加载到共享内存,而是分批次地加载、计算。如下图3所示,设一个线程块有$p$个线程,那么$N$个天体的引力计算被分到$N/p$个线程块,每个线程块分配p个天体数据大小的共享内存,分$N/P$批次串行计算。每次计算前,在同一个线程块内,各个线程相应地从全局内存加载各自对应的天体数据(通过线程id和线程块id、size计算索引)到共享内存,加载完毕之后各自迭代$p$次计算当前批次的天体引力,如下进行下去。
图3 同一个线程块分批次加载、计算
注意需要在内存加载和引力计算之后插入同步原语,保证需要计算的数据全部已经加载完毕。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 __device__ float3 calcGravitationForce (float4 bodyPos, float4 *positions, int numTiles, thread_block cta) extern __shared__ float4 sharedPos[]; float3 acc = { 0.0f , 0.0f , 0.0f }; for (unsigned int tile = 0 ; tile < numTiles; ++tile) { sharedPos[threadIdx.x] = positions[tile * blockDim.x + threadIdx.x]; sync(cta); #pragma unroll 128 for (unsigned int index = 0 ; index < blockDim.x; ++index) { acc = bodyPairInteraction(bodyPos, sharedPos[index], acc); } sync(cta); } return acc; }
通过上面的计算我们最终得到了引力的加速度数据,然后我们需要根据这个加速度更新天体的速度、位置,最后写入保存相关的数据的内存当中,比较简单,见如下CUDA的kernel代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 __global__ void integrateBodies ( float4 * newPos, float4 * oldPos, float4 *velocity, float deltaTime, float damping, unsigned int numTiles, unsigned int numBodies) thread_block cta = this_thread_block(); int index = blockIdx.x * blockDim.x + threadIdx.x; float4 pos = oldPos[index]; float3 accel = calcGravitationForce(pos, oldPos, numTiles, cta); float4 vel = velocity[index]; vel.x += accel.x * deltaTime; vel.y += accel.y * deltaTime; vel.z += accel.z * deltaTime; vel.x *= damping; vel.y *= damping; vel.z *= damping; pos.x += vel.x * deltaTime; pos.y += vel.y * deltaTime; pos.z += vel.z * deltaTime; newPos[index] = pos; velocity[index] = vel; }
最后我们需要在CPU端做一些内存映射,完成CPU与GPU的交互。这里我才用了双缓冲,即一个缓冲用于写、一个缓冲用于读,因为设置显存缓冲为只读、只写会稍微带来一些性能的提升。此外由于在CUDA模拟之后需要调用OpenGL进行渲染,我这里就采用了OpenGL与CUDA的混合编程,OpenGL和CUDA共享天体数据,这样中间不再需要经过CPU完成数据的传送,而是直接在GPU上模拟、在GPU上读取进行渲染,剩下了不少的内存传输时间。最后千万不要忘了加上cudaDeviceSynchronize语句,确保在CUDA上模拟完,否则因为一般GPU与CPU是不同步,CPU上调用完CUDA的kernel程序之后,会继续执行自己的语句序列,可能导致后面的OpenGL渲染与CUDA的访存冲突,产生一些意外的结果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 void integrateNBodySystem ( real **devicePosition, real *deviceVelocity, cudaGraphicsResource **pGRes, volatile unsigned int currentRead, float deltaTime, float damping, unsigned int numBodies, int blockSize) cudaGraphicsResourceSetMapFlags(pGRes[currentRead], cudaGraphicsMapFlagsReadOnly); cudaGraphicsResourceSetMapFlags(pGRes[1 - currentRead], cudaGraphicsMapFlagsWriteDiscard); cudaGraphicsMapResources(2 , &pGRes[0 ], 0 ); size_t bytes; cudaError_t err = cudaGetLastError(); err = cudaGraphicsResourceGetMappedPointer((void **)&devicePosition[currentRead], &bytes, pGRes[currentRead]); err = cudaGraphicsResourceGetMappedPointer((void **)&devicePosition[1 - currentRead], &bytes, pGRes[1 - currentRead]); int numBlocks = (numBodies + blockSize - 1 ) / blockSize; int sharedMemSize = blockSize * 4 * sizeof (real); integrateBodies << <numBlocks, blockSize, sharedMemSize >> > ( (float4*)devicePosition[1 - currentRead], (float4*)devicePosition[currentRead], (float4*)deviceVelocity, deltaTime, damping, numBlocks, numBodies); cudaGraphicsUnmapResources(2 , &pGRes[0 ], 0 ); } void NBodySystem::simulate(real deltaTime){ integrateNBodySystem( m_devicePosition, m_deviceVelocity, m_pGRes, m_currentRead, deltaTime, m_damping, m_numBodies, m_blockSize); cudaDeviceSynchronize(); getLastCudaError("Kernel execution failed" ); std ::swap(m_currentRead, m_currentWrite); }
3、粒子渲染-辉光特效 在天体模拟之后,我们需要把这些数据都渲染出来。对于每一个天体,我们都把它当成一个粒子,因而采用OpenGL的点精灵绘制,相关的内容比较简单,不再赘述。这里我要讲的是计算机图形学和图形处理结合实现的一种辉光特效技术,这种技术能够带来非常炫酷的渲染效果。这里说的辉光就是明亮区域产生的光晕效果,实际上是因为光线与空气中的介质相互作用,发生了散射。辉光最直接的例子就是太阳周围的光晕效果,这里我们将通过采用图像处理来实现辉光特效。
图4 无辉光、有辉光的对比
我们将在OpenGL的着色器做相关的后处理,首先需要将场景的全部渲染到两张纹理中,一张是存储正常场景渲染结果,另外一张纹理存储场面渲染结果中的亮色,可以看成是亮度图 。这里采用OpenGL的multi render target,将场景渲染到多张纹理当中。我们通过像素的rgb与权重向量$(0.2126, 0.7152, 0.0722)$做点乘得到像素的亮度值,以此来衡量一个像素点的亮度,若亮度超过给定的阈值,我们就把该像素存储到亮度图中,供后面的图像处理用。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #version 430 core uniform sampler2D image; uniform vec3 baseColor; layout(location = 0 ) out vec4 fragColor; layout(location = 1 ) out vec4 brightColor; in vec3 test; void main () fragColor = vec4(baseColor, 1.0f ); fragColor = texture(image, gl_PointCoord) * fragColor; float brightness = dot(fragColor.rgb, vec3(0.2126 , 0.7152 , 0.0722 )); if (brightness > 0.3f ) brightColor = vec4(fragColor.rgb, 1.0f ); }
接下来我们就对亮度图做一个高斯模糊处理,这属于图形处理的范畴。对于纹理的每一个像素,我们采样周围的像素,采样的范围取决于我们给定的模糊kernel半径,然后将所有采样得到的像素值根据高斯函数的做一个加权和,这样就完成了整个高斯模糊的过程。高斯函数其实就是我们熟悉的正太分布函数,它的特点就是中间的函数值大,然后向两端减少,两端是对称的。对于一个二维的图像,我们需要采用二维的高斯函数来做一个卷积处理。二维的高斯函数如下所示:
这个 网站提供了一个简单易用的高斯核函数计算工具。直接做二维的卷积非常简单,然而这里又需要考虑一个性能的问题,对于离线的图形处理来说,可能直接采样二维的邻域像素然后做加权和没什么太大的关系。但是对于实时渲染来说,这点很关键。因为$O(N^2)$和$O(N)$的差别是很大的,例如高斯模糊的kernel大小为$32\times 32$,那么对于每个像素,我们必须从周围区域采样$1024$个像素值,这仅仅针对于一个像素而言。
高斯方程有个非常巧妙的特性,它允许我们把二维方程分解为两个更小的方程:一个描述水平权重,另一个描述垂直权重。我们首先用水平权重在整个纹理上进行水平模糊,然后在经改变的纹理上进行垂直模糊,最后得到结果与原来是一样的,但是可以大大提升算法的性能,因为我们现在只需做32+32次采样了。这种方法叫做两步高斯模糊,整个算法的过程如下图5所示。
图5 两步高斯模糊
这里我实现的高斯模糊卷积核大小为$15\times 15$,采用两步模糊,只需采样30次。同时为了避免在GPU上做for循环,这里我直接将循环做一个展开。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #version 330 core in vec2 Texcoord; layout(location = 0 ) out vec4 fragColor; layout(location = 1 ) out vec4 brightColor; uniform int horizontal; uniform sampler2D Color; uniform sampler2D Bright; const float weight[8 ] = float [] (0.197448 , 0.174697 , 0.120999 , 0.065602 , 0.02784 , 0.009246 , 0.002403 , 0.000489 );void main () vec2 tex_offset = 1.0 / textureSize(Bright, 0 ); vec3 result = texture(Bright, Texcoord).rgb * weight[0 ]; result += texture(Bright, Texcoord + vec2(tex_offset.x * 1 * horizontal, tex_offset.y * 1 * (1 -horizontal))).rgb * weight[1 ]; result += texture(Bright, Texcoord - vec2(tex_offset.x * 1 * horizontal, tex_offset.y * 1 * (1 -horizontal))).rgb * weight[1 ]; result += texture(Bright, Texcoord + vec2(tex_offset.x * 2 * horizontal, tex_offset.y * 2 * (1 -horizontal))).rgb * weight[2 ]; result += texture(Bright, Texcoord - vec2(tex_offset.x * 2 * horizontal, tex_offset.y * 2 * (1 -horizontal))).rgb * weight[2 ]; result += texture(Bright, Texcoord + vec2(tex_offset.x * 3 * horizontal, tex_offset.y * 3 * (1 -horizontal))).rgb * weight[3 ]; result += texture(Bright, Texcoord - vec2(tex_offset.x * 3 * horizontal, tex_offset.y * 3 * (1 -horizontal))).rgb * weight[3 ]; result += texture(Bright, Texcoord + vec2(tex_offset.x * 4 * horizontal, tex_offset.y * 4 * (1 -horizontal))).rgb * weight[4 ]; result += texture(Bright, Texcoord - vec2(tex_offset.x * 4 * horizontal, tex_offset.y * 4 * (1 -horizontal))).rgb * weight[4 ]; result += texture(Bright, Texcoord + vec2(tex_offset.x * 5 * horizontal, tex_offset.y * 5 * (1 -horizontal))).rgb * weight[5 ]; result += texture(Bright, Texcoord - vec2(tex_offset.x * 5 * horizontal, tex_offset.y * 5 * (1 -horizontal))).rgb * weight[5 ]; result += texture(Bright, Texcoord + vec2(tex_offset.x * 6 * horizontal, tex_offset.y * 6 * (1 -horizontal))).rgb * weight[6 ]; result += texture(Bright, Texcoord - vec2(tex_offset.x * 6 * horizontal, tex_offset.y * 6 * (1 -horizontal))).rgb * weight[6 ]; result += texture(Bright, Texcoord + vec2(tex_offset.x * 7 * horizontal, tex_offset.y * 7 * (1 -horizontal))).rgb * weight[7 ]; result += texture(Bright, Texcoord - vec2(tex_offset.x * 7 * horizontal, tex_offset.y * 7 * (1 -horizontal))).rgb * weight[7 ]; brightColor = vec4(result, 1.0 ); fragColor = texture(Color, Texcoord); }
采用了两步高斯模糊之后,我们需要模糊多次,一个比较好得模糊次数是10,水平方向和垂直方向各模糊5次。为了实现两步高斯交替模糊,这里又再一次地采用了双缓冲机制,这是因为OpenGL只支持对uniform纹理的读取。具体代码见下面所示。通过以上步骤我们就得到了一张模拟的亮度图。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 bool horizontal = true ;Shader::ptr blurShader = ShaderMgr::getSingleton()->getShader(m_gaussianShaderIndex); blurShader->bind(); std ::string texStr;for (unsigned int i = 0 ; i < m_blurTimes; ++i){ m_framebuffer[m_writeIndex]->bind(); glDisable(GL_CULL_FACE); glDisable(GL_DEPTH_TEST); glDisable(GL_BLEND); glClearColor(0.0 , 0.0 , 1.0 , 1.0 ); glClear(GL_COLOR_BUFFER_BIT); blurShader->setInt("Color" , 0 ); blurShader->setInt("Bright" , 1 ); blurShader->setInt("horizontal" , horizontal); std ::stringstream iss; iss << m_readIndex; TextureMgr::getSingleton()->bindTexture("Color" + iss.str(), 0 ); TextureMgr::getSingleton()->bindTexture("BrightColor" + iss.str(), 1 ); MeshMgr::getSingleton()->drawMesh(m_screenQuadIndex, false , 0 ); std ::swap(m_readIndex, m_writeIndex); horizontal = !horizontal; } blurShader->unBind();
最后为了实现辉光效果,我们需要将模糊的亮度图叠加到场景渲染结果上,这样辉光特效就制作好了。
1 2 3 4 5 6 7 8 9 10 11 12 13 #version 330 core in vec2 Texcoord; out vec4 fragColor; uniform sampler2D Color; uniform sampler2D BrightColor; void main () vec3 hdrColor = (texture(Color, Texcoord).rgb + texture(BrightColor, Texcoord).rgb); fragColor = vec4(hdrColor, 1.0f ); }
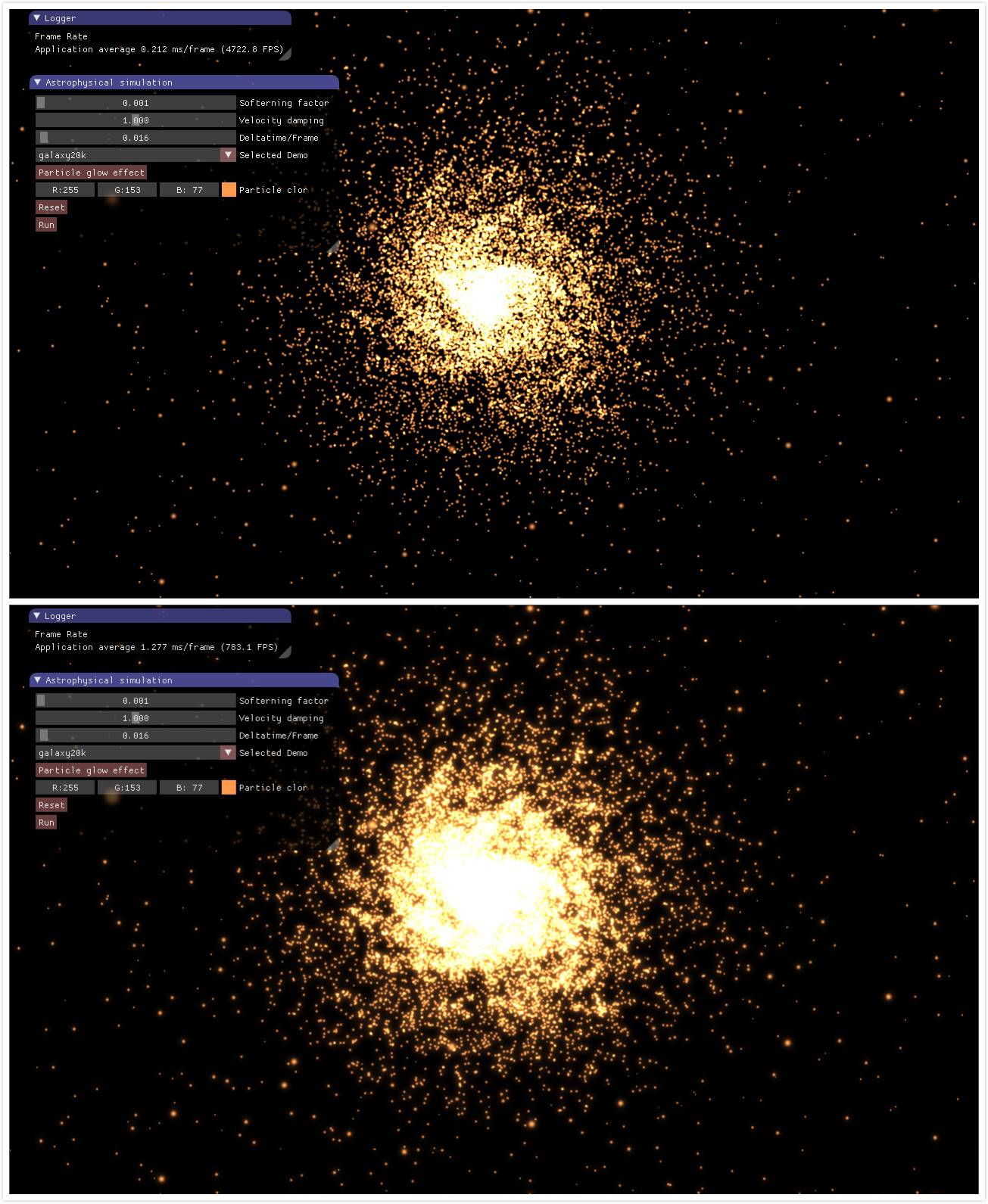
下面是无辉光特效、有辉光特效的一个对比图,可以看到差别非常明显,辉光效果可以极大地提升场景中的效果。
图6 无辉光(上)、有辉光(下)对比
4、模拟效果 文章开头模拟的是银河星系。下面这个是银河星系与仙女座星系碰撞。
星系膨胀。
参考资料: $[1]$ Aarseth, S. 2003. Gravitational N-Body Simulations. Cambridge University Press. Barnes, J., and P. Hut. 1986. “A Hierarchical O(n log n) Force Calculation Algorithm.” Nature 324.
$[2]$ Greengard, Leslie F., and Jingfang Huang. 2002. “A New Version of the Fast Multipole Method for Screened Coulomb Interactions in Three Dimensions.” Journal of Computational Physics 180(2), pp. 642–658.
$[3]$ Darden, T., D. York, and L. Pederson. 1993. “Particle Mesh Ewald: An N log(N) Method for Ewald Sums in Large Systems.” Journal of Chemical Physics 98(12), p. 10089.
$[4]$ CUDA C Programming Guide
$[5]$ N-Body Data Archive
$[6]$ Lars Nyland, Mark Harris, Jan Prins.《GPU Germ3》 Chapter 31: Fast N-Body Simulation with CUDA.