本篇文章主要是关于三维网格模型的基于GPU并行的体素化算法,这个算法我是偶然从NVIDIA官网上看到的。基于GPU的体素化算法巧妙地借助了渲染流程的光栅化处理,将整个体素化的过程并行化,速度极快,缺点就是占用的内存较高。相关的完整代码请看这个链接 中的Renderer目录下的Voxelization.h文件和Voxelization.cpp文件。
在基于位置动力学的物理模拟中,所有要模拟的物体都由一组粒子来表示,每个粒子都是一个给定半径大小的球体,对于固体这类的物体,粒子通常是紧密相连的。为此,为了实现基于位置动力学的物理模拟,我们需要采用一种算法将网格物体的三角网格模型用一个个粒子表示 ,这个并不是简单地取网格模型的所有顶点就行,因为我们需要紧密连接的粒子,面片网格模型的顶点通常是稀疏的。这个过程其实就是体素化,三维体素是二维像素的三维扩展,体素的基本单元不再是二维的正方形,而是三维的立方体,立方体的边长决定了体素化的分辨率,通常边长越长,则分辨率越低。将网格体素化后我们得到了一组体素的中心顶点位置,可将其用于后续的基于位置动力学的物理模拟当中。
目前常用的体素化方法大都是基于CPU的,这类方法通常是将射线与物体求交,根据是奇数个交点还是偶数个交点来判断当前的体素是否在物体的内部。在没有采用特殊的数据结构时,每次求交都要遍历一次网格模型的所有三角形,效率非常低。在采用了八叉树加速之后,速度有所提升,但随着模型的三角形面片数增加,串行的体素化算法耗费的时间越来越长。我没有采用CPU串行的体素化方法,而是采用了基于GPU并行的体素化算法,这个算法我是偶然从NVIDIA官网上看到的。基于GPU的体素化算法巧妙地借助了渲染流程的光栅化处理,将整个体素化的过程并行化,速度极快,缺点就是占用的内存较高。
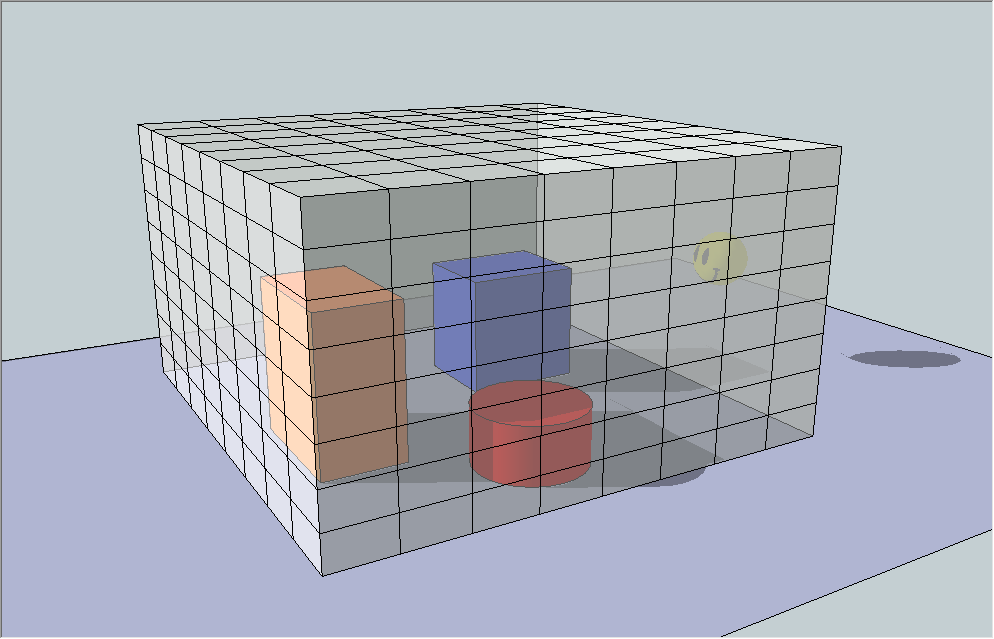
图1 三维体素模型 一、体素化 基于GPU的三维体素化大致思想就是:首先计算出需要体素化模型的AABB包围盒,然后将模型投影到AABB包围盒的某个平面上,经过渲染管线的光栅化插值操作,我们可以在片元着色器得到每个像素点对应的世界空间的顶点坐标,根据这个顶点坐标标记三维空间数组(这个三维空间数组就是根据体素划分的空间序列)的相应位置,最后在CPU端读出这个三维空间数组,若当前的数组位置有标记,则将该数组位置对应的立方体作为一个体素。可以看到,整个流程思路非常清晰,但是还需要借助一些手段修正算法存在的缺陷,这个在后面会提到。
首先就是计算网格模型的AABB包围盒,在导入模型时获取$x$、$y$、$z$轴分量的最大值和最小值,从而得到包围盒的最大顶点和最小顶点。这个比较简单,不再赘述:
1 2 3 4 5 6 7 8 9 10 11 12 13 if (mesh->mVertices[x].x < m_min.x) m_min.x = mesh->mVertices[x].x; if (mesh->mVertices[x].y < m_min.y) m_min.y = mesh->mVertices[x].y; if (mesh->mVertices[x].z < m_min.z) m_min.z = mesh->mVertices[x].z; if (mesh->mVertices[x].x > m_max.x) m_max.x = mesh->mVertices[x].x; if (mesh->mVertices[x].y > m_max.y) m_max.y = mesh->mVertices[x].y; if (mesh->mVertices[x].z > m_max.z) m_max.z = mesh->mVertices[x].z;
图2 模型包围盒
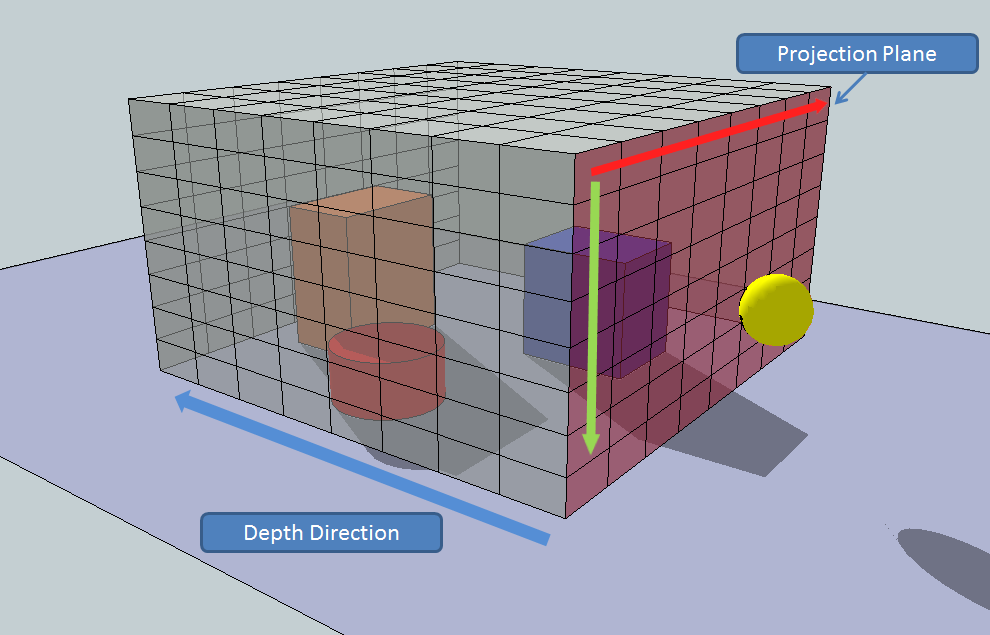
获取了模型的包围盒之后,我们就需要根据这个包围盒设置我们的观察角度和投影平面,这关系到后面的体素化结果。同时为了保证正确地体素化模型,我们采用的投影方式是正交投影 。首先我们要选择一个观察方向和投影平面,AABB包围盒有六个面,其中前和后、上和下、左和右的投影结果是一样的,因此实际的选择只有三个平面,分别是前、上、右(或者后、下、左)。显然一个物体投影到这个三个平面上的结果都不一样,目前我们暂时先选择投影到前面这个平面上,摄像机的视线朝向z轴的负方向。注意正确地设置摄像机的位置,否则什么看不到。既然我们选择投影到前面这个平面上,我们就设置摄像机的位置在包围盒前面这个平面的中心再往前一点。同时了为了确保模型全部投影到屏幕上,我们设置的正交投影平面比选定的包围盒平面稍微大一点点。具体代码如下所示:
图3 三个面上的投影结果
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 glm::vec3 min, max; glm::ivec3 resolution; target->getAABB(min, max); glm::vec3 range (max.x - min.x, max.y - min.y, max.z - min.z) ; resolution.x = static_cast <int >(range.x / step); resolution.y = static_cast <int >(range.y / step); resolution.z = static_cast <int >(range.z / step); int length = static_cast <int >(resolution.x * resolution.y * resolution.z);glm::vec3 cameraPos; cameraPos.x = (min.x + max.x) * 0.5f ; cameraPos.y = (min.y + max.y) * 0.5f ; cameraPos.z = max.z + 0.2f ; FPSCamera::ptr camera (new FPSCamera(cameraPos)) ; camera->lookAt(glm::vec3(0.0f , 0.0f , -1.0f )); camera->setOrthographicProject(-range.x * 0.51 , +range.x * 0.51 , -range.y * 0.51 , +range.y * 0.51 , 0.1 , range.z * 1.2f + 0.2f );
图4 包围盒投影平面
设置好投影矩阵和视图矩阵之后,我们需要申请一个着色器可写的缓冲,这个缓冲的大小等于AABB包围盒的分辨率,在片元着色器阶段我们需要根据当前片元的世界空间位置对这个缓冲做标记,表示该缓冲位置上有一个体素。我们采用OpenGL的GL_SHADER_STORAGE_BUFFER,这是一个着色器可读写的缓冲类型。申请缓冲之后,将缓冲全部初始化为0。然后将需要体素化的网格模型送入渲染管线进行渲染。在片元着色器中,将每个片元的世界空间位置对应的缓冲位置加1。最后在CPU端读出缓冲内容,缓冲值大于0时,则表示该位置有一个体素。CPU端的整个流程代码如下所示。这里需要特别注意的是,我们应该关闭深度测试和背面剔除,保证模型的全面三角形都进入片元着色器,确保所有的三角形不被剔除,从而使得全部的三角形都被处理,最后得到正确的体素化结果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 bool Voxelization::voxelize(Drawable* target, const float & step, std ::vector <glm::vec3>& ret){ ShaderMgr::ptr shaderMgr = ShaderMgr::getSingleton(); unsigned int voxelizeCount = shaderMgr->loadShader("voxelizeCount" , "./glsl/voxelizeCount.vert" , "./glsl/voxelizeCount.frag" ); Shader::ptr shader = shaderMgr->getShader(voxelizeCount); glm::vec3 min, max; glm::ivec3 resolution; target->getAABB(min, max); glm::vec3 range (max.x - min.x, max.y - min.y, max.z - min.z) ; resolution.x = static_cast <int >(range.x / step) + 1 ; resolution.y = static_cast <int >(range.y / step) + 1 ; resolution.z = static_cast <int >(range.z / step) + 1 ; int length = static_cast <int >(resolution.x * resolution.y * resolution.z); glm::vec3 cameraPos; cameraPos.x = (min.x + max.x) * 0.5f ; cameraPos.y = (min.y + max.y) * 0.5f ; cameraPos.z = max.z + 0.2f ; FPSCamera::ptr camera (new FPSCamera(cameraPos)) ; camera->lookAt(glm::vec3(0.0f , 0.0f , -1.0f )); camera->setOrthographicProject(-range.x * 0.51 , +range.x * 0.51 , -range.y * 0.51 , +range.y * 0.51 , 0.1 , range.z * 1.2f + 0.2f ); glPolygonMode(GL_FRONT_AND_BACK, GL_FILL); glDisable(GL_CULL_FACE); glDisable(GL_DEPTH_TEST); glClearColor(1.0f , 0.0f , 0.0f , 1.0f ); glClear(GL_COLOR_BUFFER_BIT); glGenBuffers(1 , &m_cntBuffer); glBindBuffer(GL_SHADER_STORAGE_BUFFER, m_cntBuffer); glBufferData(GL_SHADER_STORAGE_BUFFER, length * sizeof (int ), nullptr , GL_STATIC_DRAW); glBindBufferBase(GL_SHADER_STORAGE_BUFFER, 0 , m_cntBuffer); shader->bind(); shader->setVec3("boxMin" , min); shader->setFloat("step" , step); shader->setVec3("resolution" , resolution); int *writePtr = reinterpret_cast <int *>(glMapBuffer(GL_SHADER_STORAGE_BUFFER, GL_WRITE_ONLY)); for (int x = 0 ; x < length; ++x) { writePtr[x] = 0 ; } if (!glUnmapBuffer(GL_SHADER_STORAGE_BUFFER)) std ::cout << "unMap error\n" << std ::endl ; target->render(camera, nullptr , nullptr , shader); glMemoryBarrier(GL_SHADER_STORAGE_BARRIER_BIT); glBindBuffer(GL_SHADER_STORAGE_BUFFER, m_cntBuffer); int *readPtr = reinterpret_cast <int *>(glMapBuffer(GL_SHADER_STORAGE_BUFFER, GL_READ_ONLY)); if (readPtr != nullptr ) { for (int x = 0 ; x < length; ++x) { if (*(readPtr + x) != 0 ) { int iy = x / (resolution.x * resolution.z); int iz = (x - iy * resolution.x * resolution.z) / (resolution.x); int ix = x - iy * resolution.x * resolution.z - iz * resolution.x; ret.push_back(min + glm::vec3(ix * step, iy * step, iz * step)); } } } else { std ::cout << "nullptr error!\n" ; } glUnmapBuffer(m_cntBuffer); glBindBuffer(GL_SHADER_STORAGE_BUFFER, 0 ); glDeleteBuffers(1 , &m_cntBuffer); return false ; }
接下来就需要在着色器中做一些操作。首先是顶点着色器,在顶点着色器中并没有什么复杂的操作,我们需要将当前的顶点位置传到片元着色器,借助渲染管线的光栅化功能,从而在片元着色器中得到每个片元对应的世界空间位置。下面顶点着色器的代码,其余部分乘上视图矩阵和投影矩阵就不说了。
1 2 3 4 5 6 7 8 9 10 11 12 #version 430 core layout (location = 0 ) in vec3 position; out vec3 FragPos; uniform mat4 viewMatrix; uniform mat4 projectMatrix; void main () FragPos = position; gl_Position = projectMatrix * viewMatrix * vec4(position,1.0f ); }
中间经过光栅化处理,我们在片元着色器得到每个片元的世界空间坐标。根据这个世界空间的坐标去索引计数缓冲,注意这里采用了GLSL的原子操作函数atmoicAdd,避免GPU线程之间的写冲突。缓冲下标索引的计算基本就是根据体素的大小和包围盒来确定。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 #version 430 core in vec3 FragPos; layout (std430, binding = 0 ) buffer CountBuffer{ int cnts[]; }; uniform float step; uniform vec3 boxMin; uniform vec3 resolution; out vec4 color; void main () int x = int ((FragPos.x - boxMin.x)/step); int y = int ((FragPos.y - boxMin.y)/step); int z = int ((FragPos.z - boxMin.z)/step); int index = int (y * (resolution.z * resolution.x) + z * resolution.x + x); atomicAdd(cnts[index], 1 ); color = vec4(0.0 ,1.0 ,0.0 ,1.0 ); }
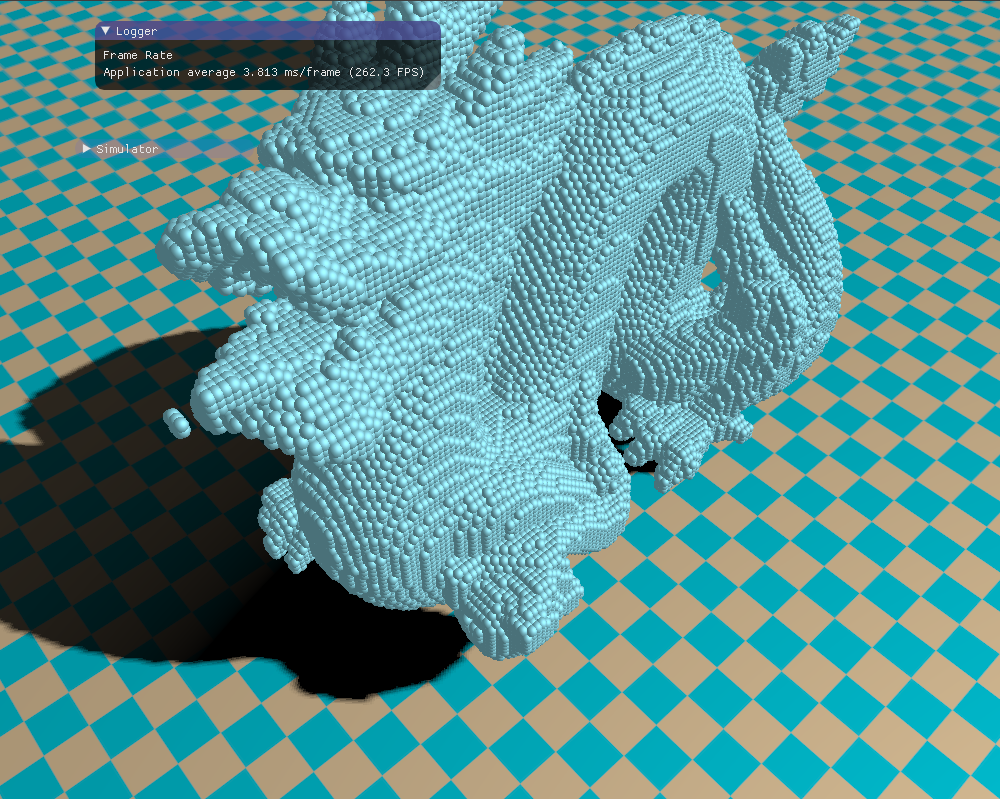
然后下面就是我实现的体素化效果,每个体素用一个立方体绘制,当然也可以用球体绘制。看起来颇有游戏《我的世界》的风格。
二、修补裂缝 上面的实现效果看起来貌似非常不错,但是却存在一个非常严重的问题。前面我们在选择投影平面的时候固定投影在了z轴方向的包围盒平面,这是问题产生的根源。因为模型的每个三角形面片在每个包围盒投影面上的投影结果都不同,若当前的三角形与选取的投影面垂直,那么三角形投影到平面上的将是一条直线,这丢失了很多信息,从而导致裂缝的产生。
图5 不同投影平面的体素化结果
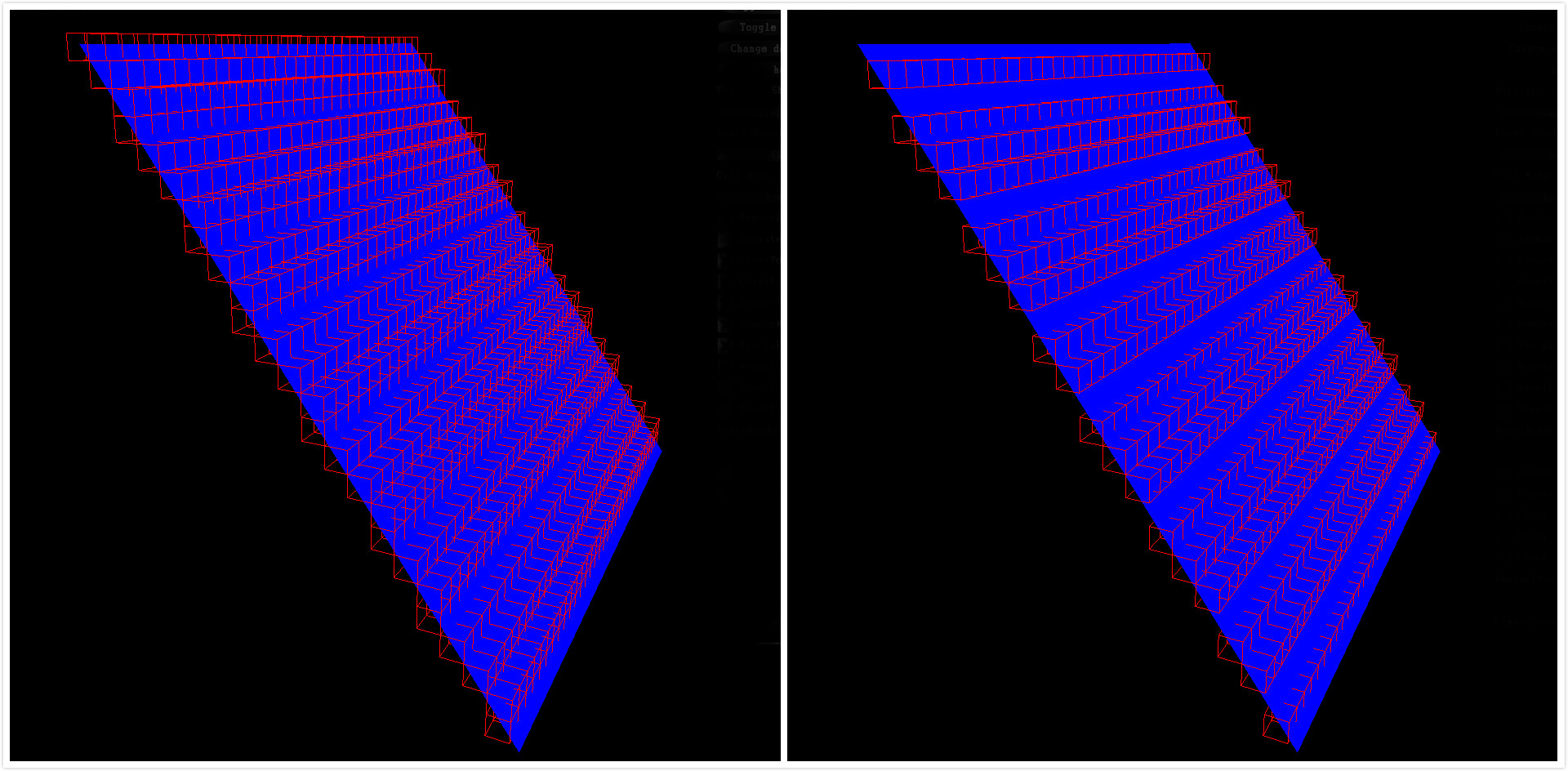
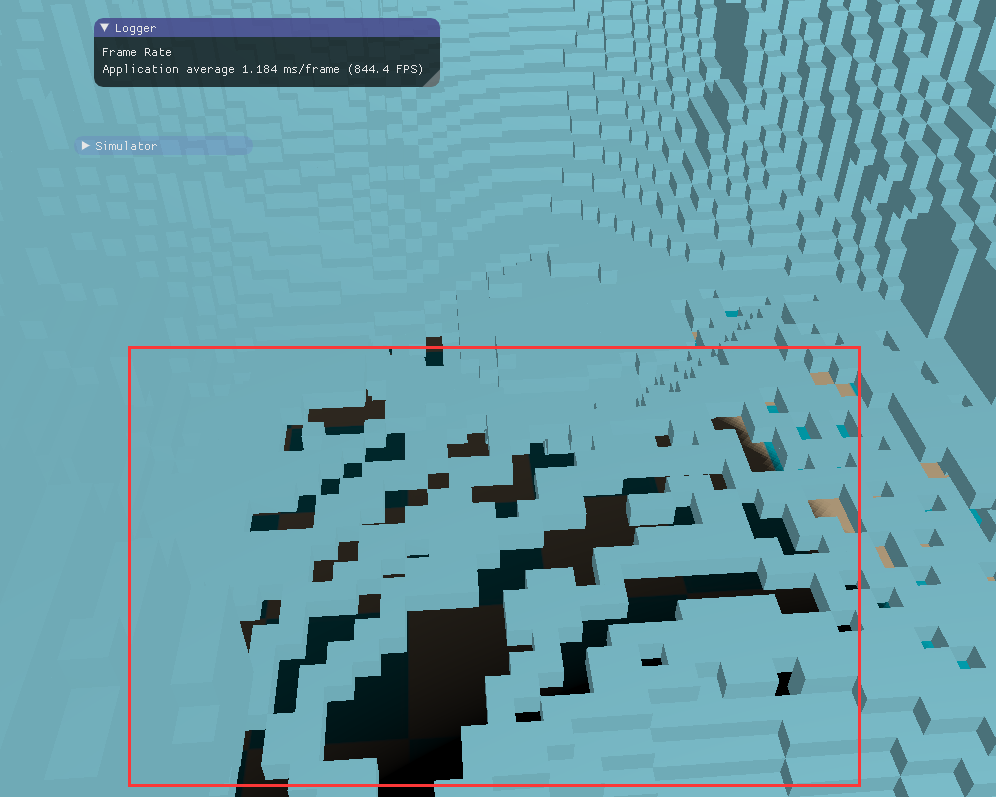
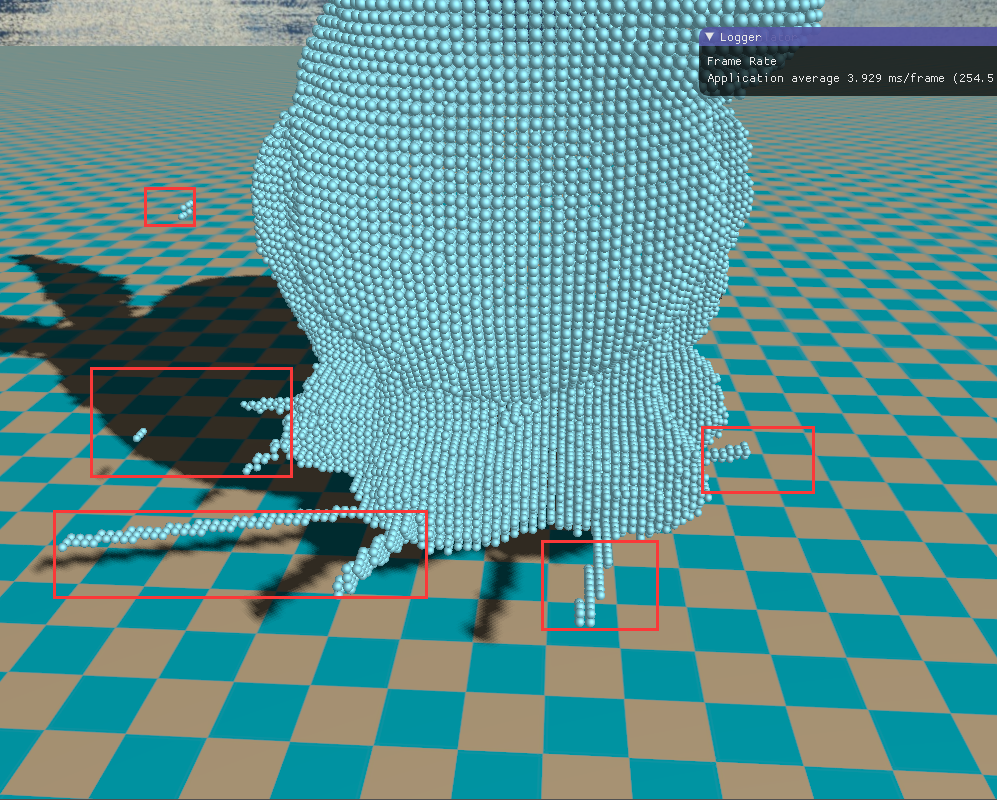
图5中,左图选取的投影面是摄像机在右边,朝向坐标,这时光栅化得到的结果很好,因而体素化的结果也很好。但是右边的这张图选取的投影面是摄像机在上面,朝向下边,这时光栅化得到的几何面片较少,很多相邻的位置都被投影到了一个片元像素,一些地方没有被体素化,从而导致了裂缝的产生!下面是我实现的程序产生的裂缝,选取的投影方向是z轴方向,下图中的红框部分的几何面片几乎平行于xz平面,从而导致投影光栅化产生的是一个被“压缩“的结果。由于裂缝非常明显且几乎必然会产生(因为通常模型都很复杂,三角形面片朝向很随机),因此有必要采取一些措施来修补这些裂缝。
图6 根据前面步骤产生的裂缝
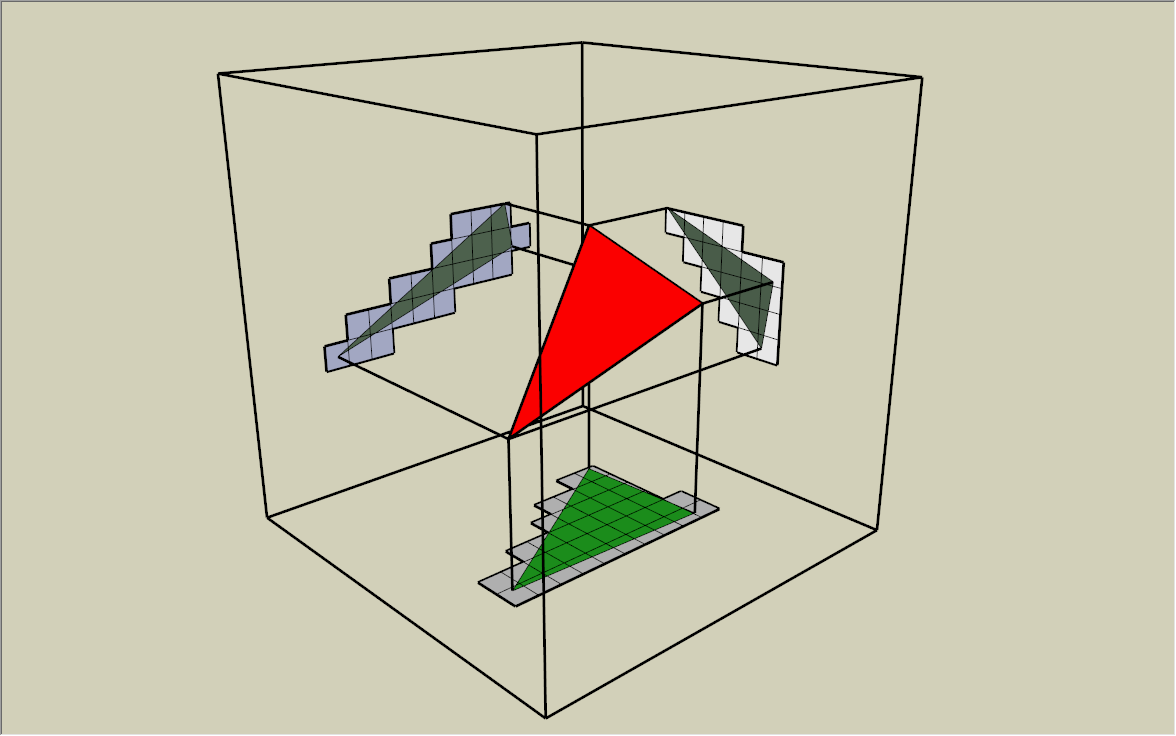
如前面的图3所示,每个三角形面片在不同包围盒投影面上的投影结果不同,根据三角形的朝向不同,投影到平面上的三角形大小也各不相同。裂缝产生的原因就是因为投影到平面上的三角形面积被”压缩“了,因此我们需要选取一个投影方向,在该投影方向上三角形的投影面积最大,这样就能够确保所有的三角形面片被充分地体素化,从而使得裂缝小时。
图7 分别投影到包围盒的右、上、前平面上
因此,我们首先创建三个投影摄像机,将物体分别投影到沿着$x$、$y$、$z$轴的平面上,如图7所示,用以后面着色器中根据三角形的投影面积做选择。代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 float offset = 0.2f ;glm::vec3 cameraPosZ, cameraPosX, cameraPosY; cameraPosZ.x = (min.x + max.x) * 0.5f ; cameraPosZ.y = (min.y + max.y) * 0.5f ; cameraPosZ.z = max.z + offset; FPSCamera::ptr cameraZ (new FPSCamera(cameraPosZ)) ; cameraZ->lookAt(glm::vec3(0.0f , 0.0f , -1.0f ), Camera3D::LocalUp); cameraZ->setOrthographicProject(-range.x * 0.51 , +range.x * 0.51 , -range.y * 0.51 , +range.y * 0.51 , 0.1 , range.z * 1.2f + offset); cameraPosX.x = max.x + offset; cameraPosX.y = (min.y + max.y) * 0.5f ; cameraPosX.z = (min.z + max.z) * 0.5f ; FPSCamera::ptr cameraX (new FPSCamera(cameraPosX)) ; cameraX->lookAt(glm::vec3(-1.0f , 0.0f , 0.0f ), Camera3D::LocalUp); cameraX->setOrthographicProject(-range.z * 0.51 , +range.z * 0.51 , -range.y * 0.51 , +range.y * 0.51 , 0.1 , range.x * 1.2f + offset); cameraPosY.x = (min.x + max.x) * 0.5f ; cameraPosY.y = max.y + offset; cameraPosY.z = (min.z + max.z) * 0.5f ; FPSCamera::ptr cameraY (new FPSCamera(cameraPosY)) ; cameraY->lookAt(glm::vec3(0.0f , -1.0f , 0.0f ), glm::vec3(0 , 1.0 , 0.001 )); cameraY->setOrthographicProject(-range.x * 0.51 , +range.x * 0.51 , -range.z * 0.51 , +range.z * 0.51 , 0.1 , range.y * 1.2f + offset); ...... shader->setMat4("viewProject[0]" , cameraX->getProjectMatrix() * cameraX->getViewMatrix()); shader->setMat4("viewProject[1]" , cameraY->getProjectMatrix() * cameraY->getViewMatrix()); shader->setMat4("viewProject[2]" , cameraZ->getProjectMatrix() * cameraZ->getViewMatrix());
接下来我们将用到几何着色器 ,几何着色器阶段在顶点着色器之后、光栅化之前,它根据给定的输入图元和输出图元进行相关的几何图元操作,正好我们可以接用它来根据三角形的投影面积选择采用哪一个投影相机。这里有一个技巧,直观上我们说是根据三角形的投影面积来渲染采用哪个投影相机,实际上没有必要真正地去计算三角形的投影面积,我们可以直接根据当前三角形的世界空间法线朝向来决定投影方向 。举个例子,当法线向量的x分量比其余两个分量大时,则当前的三角形肯定投影到x轴方向的投影平面上的面积更大。更深入的理解:设法线向量为$n=(nx,ny,nz)$,我们将法线向量$n$与$(1,0,0)$、$(0,1,0)$、$(0,0,1)$分别做点乘,结果为$nx$、$ny$、$nz$,而法线向量分别与该三个基向量点乘的意义为法线向量在$x$、$y$、$z$轴上的投影值,该值越大则三角形投影到该平面上的面积也越大。所以,我们直接根据最大的法线分量来选择采用哪个投影相机 。如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 uint selectViewProject () vec3 p1 = gl_in[1 ].gl_Position.xyz - gl_in[0 ].gl_Position.xyz; vec3 p2 = gl_in[2 ].gl_Position.xyz - gl_in[0 ].gl_Position.xyz; vec3 faceNormal = cross(p1, p2); float nDX = abs (faceNormal.x); float nDY = abs (faceNormal.y); float nDZ = abs (faceNormal.z); if ( nDX > nDY && nDX > nDZ ) { return 0 ; } else if ( nDY > nDX && nDY > nDZ ) { return 1 ; } else { return 2 ; } }
然后我们将上述的代码应用到我们的几何着色器中,因为视图投影过程挪到了几何着色器阶段,所以顶点着色器直接输入顶点的位置,不做任何变换。几何着色器设置输入图元为三角形,输出图元为最大顶点数为3的三角形带,设置一个viewProject的uniform数组。通过几何着色器,我们对模型的每个三角形面片都做了一个投影选择的处理。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 #version 430 core layout (location = 0 ) in vec3 position; void main () gl_Position = vec4(position, 1.0f ); } #version 430 core layout (triangles) in; layout (triangle_strip, max_vertices = 3 ) out; out vec3 FragPos; uniform mat4 viewProject[3 ]; uint selectViewProject () vec3 p1 = gl_in[1 ].gl_Position.xyz - gl_in[0 ].gl_Position.xyz; vec3 p2 = gl_in[2 ].gl_Position.xyz - gl_in[0 ].gl_Position.xyz; vec3 faceNormal = cross(p1, p2); float nDX = abs (faceNormal.x); float nDY = abs (faceNormal.y); float nDZ = abs (faceNormal.z); if ( nDX > nDY && nDX > nDZ ) { return 0 ; } else if ( nDY > nDX && nDY > nDZ ) { return 1 ; } else { return 2 ; } } void main () uint projectIndex = selectViewProject(); FragPos = gl_in[0 ].gl_Position.xyz; gl_Position = viewProject[projectIndex] * gl_in[0 ].gl_Position; EmitVertex(); FragPos = gl_in[1 ].gl_Position.xyz; gl_Position = viewProject[projectIndex] * gl_in[1 ].gl_Position; EmitVertex(); FragPos = gl_in[2 ].gl_Position.xyz; gl_Position = viewProject[projectIndex] * gl_in[2 ].gl_Position; EmitVertex(); EndPrimitive(); }
最终,我们成功的修补了体素的裂缝,如下图所示,先前的裂缝已经填上了体素。
图8 成功修补裂缝
三、修补孔洞 然而,通过前面2部分的处理,另外一个问题出现了。由于模型的每个三角形都是各自根据在每个平面上的投影面积来选择投影相机,这意味着两个相邻的三角形片面可能选取了不同投影相机,使得三角形面片之间因为体素化投影平面的不同而产生过渡问题,从而出现孔洞,即有些部分没有被体素化到。如下图9所示。
图9 体素孔洞
孔洞的产生根源于光栅化处理,一个像素是否作为当前图元的光栅片元,是通过判断当前图元是否覆盖了该像素中心来完成的。对于那些没有覆盖像素中心的片元,不作为该图元的光栅片元送入片元着色器做进一步的处理,因而模型的一些部分可能会被丢失,从而造成孔洞。为了解决这个问题,我们将在几何着色器中实现一种被称为保守光栅化 (Conservative Rasterization)的算法,依旧在几何着色器中实现。
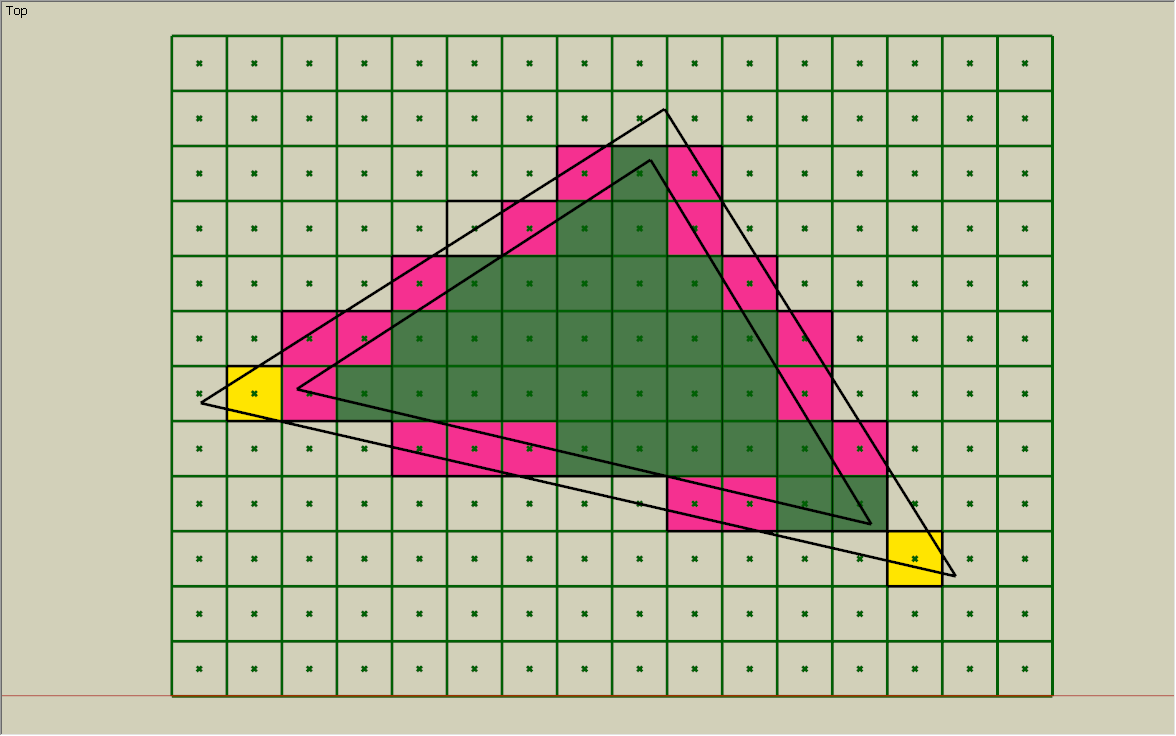
通常的硬件光栅化,都是默认只取那些中心被图元覆盖的像素单元。而保守光栅化则将所有被图元覆盖(无论是否覆盖到像素单元的中心点)的像素单元都作为光栅化的片元,从而确保图元覆盖的所有区域都被光栅化,故名思意,这就是“保守”一词的由来。如下图10所示,通常情况下硬件默认的光栅片元是绿色部分,边缘红色部分的片元没有被光栅化,导致我们的体素化结果出现孔洞。为了修补体素化的孔洞,我们必须使得被图元哪怕一点点覆盖到的像素(就是下图中的红色部分)都作为当前图元的光栅化结果,这个过程就是保守光栅化算法。
图10 保守光栅化
那么怎么实现保守光栅化算法,使得上面的红色部分也被光栅化到呢?一个简单直观的思路就是手动扩充三角形图元面片。如上图10所示,里面的三角形是最初的我们要光栅化的三角形,为了使得边缘红色的像素也包含进来,我们扩张最初的三角形得到外面的那个三角形,这个三角形比原来的三角形稍微大一点,此时若将该扩大的三角形送入硬件默认的光栅化单元进行处理,则红色像素也被当作光栅片元,从而达到了我们的目的。 注意,这里三角形的扩大程度非常关键,上面的扩大的三角形将我们不需要的像素单元也包含了进来,即黄色像素部分,我们将通过计算三角形的包围盒来剔除那些黄色像素单元,剔除像素部分我们将在片元着色器中实现。下图11是我实现的保守光栅化(图右)效果,图左是默认光栅化的效果。
图11 默认的光栅化和保守光栅化对比
扩大三角形和剔除像素整个过程都是在裁剪空间中进行的,也就是经过摄像机空间变换和投影变换之后。故而三角形的包围盒只需二维即可,然后需要适当地扩大一点,以免剔除红色的像素片元。一个裁剪空间的三角形包围盒计算如下所示,我们采用GLSL的vec4存储包围盒的最小顶点和最大顶点。
1 2 3 4 5 6 7 8 9 10 vec4 calcAABB (vec4 pos[3 ], vec2 pixelDiagonal) vec4 aabb; aabb.xy = min(pos[2 ].xy, min(pos[1 ].xy, pos[0 ].xy)); aabb.zw = max(pos[2 ].xy, max(pos[1 ].xy, pos[0 ].xy)); aabb.xy -= pixelDiagonal; aabb.zw += pixelDiagonal; return aabb; }
接下来对于给定的三角形的三个顶点,我们要适当地扩大三角形。总体的思路就是:首先计算三角形的三条边与原点构成的齐次空间的平面,然后适当挪动这三个平面,接着就计算偏移后的这三个齐次平面的交线,最后计算三条交线与三角形平面的交点,从而得到扩大后的三角形的三个顶点。 整个计算过程都是在裁剪空间中进行的,所以我们忽略顶点的$z$分量,但是上面又提到了齐次平面一词,我们采用一个齐次平面来描述三角形边的线段。所谓齐次平面,就是我们把顶点的齐次分量$w$和$x$、$y$分量合并一起来表示一条线段,直观来看,这就是一个齐次空间的平面,但实际上就是一段二维空间的直线。如下所示:
公式$(1)$就是一个齐次空间的过原点的平面方程,但是它实际上就是一个二维空间的直线方程。这是因为我们采用的都是正交投影,正交投影并没有透视除法之类的处理,因为正交投影都是线性变换,故而$w_c=1$,所以公式$(1)$表示的过原点的齐次空间的平面方程就是如下所示的二维直线方程:
之所以采用齐次空间的平面方程,是为了方便我们的计算。首先我们根据三角形的三条边计算三个齐次空间的平面,我们已知该齐次空间的平面过原点,平面方程的$(A,B,C)$就是该平面的法线向量,我们直接做叉乘计算可得平面的法线,如下所示:
1 2 3 4 vec3 edgePlanes[3 ]; edgePlanes[0 ] = cross(pos[0 ].xyw - pos[2 ].xyw, pos[2 ].xyw); edgePlanes[1 ] = cross(pos[1 ].xyw - pos[0 ].xyw, pos[0 ].xyw); edgePlanes[2 ] = cross(pos[2 ].xyw - pos[1 ].xyw, pos[1 ].xyw);
然后对这三个平面分别进行偏移。直观上来说,我们分别令三角形的三条边在其法线的方向上挪一段距离,这个距离由像素单元格的大小(即下面的halfPixel)在法线方向的投影决定,如下所示:
1 2 3 edgePlanes[0 ].z -= dot(halfPixel[projectIndex], abs (edgePlanes[0 ].xy)); edgePlanes[1 ].z -= dot(halfPixel[projectIndex], abs (edgePlanes[1 ].xy)); edgePlanes[2 ].z -= dot(halfPixel[projectIndex], abs (edgePlanes[2 ].xy));
接着计算三个齐次平面的交线向量,这个不难理解,两个平面的交线必然垂直于这两个平面的法线向量,因而交线向量可由这两个平面的法线向量做叉乘得到:
1 2 3 4 5 6 7 vec3 intersection[3 ]; intersection[0 ] = cross(edgePlanes[0 ], edgePlanes[1 ]); intersection[1 ] = cross(edgePlanes[1 ], edgePlanes[2 ]); intersection[2 ] = cross(edgePlanes[2 ], edgePlanes[0 ]); intersection[0 ] /= intersection[0 ].z; intersection[1 ] /= intersection[1 ].z; intersection[2 ] /= intersection[2 ].z;
最后我们根据上面的三条射线向量与初试三角形所在的平面求交点,从而得到最终扩大后的三角形的三个顶点。由于我们是正交投影,所以上面求到的三条射线向量的$x$分量和$y$分量就是扩大三角形顶点的$x$分量和$y$分量,即交点的$x$、$y$已知,需要求$z$值。一个三维平面方程如下所示,从直观的几何意义上来说,$(A,B,C)$就是平面的法线向量,$D$就是原点到平面的直线距离。
已知初始三角形的三个点,我们可以求出它的法线向量,然后原点到平面的直线距离就等于平面上的点在法线向量方向上的投影长度,这里要特别注意符号,具体看下面的代码:
1 2 3 vec4 trianglePlane; trianglePlane.xyz = normalize(cross(pos[1 ].xyz - pos[0 ].xyz, pos[2 ].xyz-pos[0 ].xyz)); trianglePlane.w = -dot(pos[0 ].xyz, trianglePlane.xyz);
然后还需要提一点的是,我们要确保输入的三角形的顶点环绕顺序都是逆时针方向,这个逆时针方向是针对当前的相机投影方向。对于背向的面片,我们要做一个纠正的过程。判断是否是背向面片很简单,只需通过计算三角形法线向量与$(0,0,1)$做点乘,判断其符号即可。
1 2 3 4 5 6 7 if (dot(trianglePlane.xyz, vec3(0.0 , 0.0 , 1.0 )) < 0.0 ){ vec4 vertexTemp = pos[2 ]; pos[2 ] = pos[1 ]; pos[1 ] = vertexTemp; }
已知交点的$x$和$y$,我们代入平面方程$(3)$求得$z$值。
1 2 3 4 5 6 7 8 float z[3 ];z[0 ] = -(intersection[0 ].x * trianglePlane.x + intersection[0 ].y * trianglePlane.y + trianglePlane.w) / trianglePlane.z; z[1 ] = -(intersection[1 ].x * trianglePlane.x + intersection[1 ].y * trianglePlane.y + trianglePlane.w) / trianglePlane.z; z[2 ] = -(intersection[2 ].x * trianglePlane.x + intersection[2 ].y * trianglePlane.y + trianglePlane.w) / trianglePlane.z; pos[0 ].xyz = vec3(intersection[0 ].xy, z[0 ]); pos[1 ].xyz = vec3(intersection[1 ].xy, z[1 ]); pos[2 ].xyz = vec3(intersection[2 ].xy, z[2 ]);
最终,我们求得到扩大后的三角形的三个顶点,我们还需要对三个顶点做逆视图投影变换,将裁剪空间的顶点变换到世界空间,得到扩大后的三角形的世界坐标,因为我们最终目的是根据世界空间坐标做体素化的处理。与此同时,我们还将在裁剪空间的扩大三角形的顶点传到片元着色器,因为我们要剔除不必要的片元。以下是保守光栅化算法的几何着色器代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 #version 430 core layout (triangles) in; layout (triangle_strip, max_vertices = 3 ) out; out vec3 FragPos; out vec3 ProjectPos; out vec4 BoundingBox; uniform vec2 halfPixel[3 ]; uniform mat4 viewProject[3 ]; uniform mat4 viewProjectInverse[3 ]; uint selectViewProject () vec3 p1 = gl_in[1 ].gl_Position.xyz - gl_in[0 ].gl_Position.xyz; vec3 p2 = gl_in[2 ].gl_Position.xyz - gl_in[0 ].gl_Position.xyz; vec3 faceNormal = cross(p1, p2); float nDX = abs (faceNormal.x); float nDY = abs (faceNormal.y); float nDZ = abs (faceNormal.z); if ( nDX > nDY && nDX > nDZ ) { return 0 ; } else if ( nDY > nDX && nDY > nDZ ) { return 1 ; } else { return 2 ; } } vec4 calcAABB (vec4 pos[3 ], vec2 pixelDiagonal) vec4 aabb; aabb.xy = min(pos[2 ].xy, min(pos[1 ].xy, pos[0 ].xy)); aabb.zw = max(pos[2 ].xy, max(pos[1 ].xy, pos[0 ].xy)); aabb.xy -= pixelDiagonal; aabb.zw += pixelDiagonal; return aabb; } void main () uint projectIndex = selectViewProject(); vec4 pos[3 ] = vec4[3 ] ( viewProject[projectIndex] * gl_in[0 ].gl_Position, viewProject[projectIndex] * gl_in[1 ].gl_Position, viewProject[projectIndex] * gl_in[2 ].gl_Position ); vec4 trianglePlane; trianglePlane.xyz = normalize(cross(pos[1 ].xyz - pos[0 ].xyz, pos[2 ].xyz - pos[0 ].xyz)); trianglePlane.w = -dot(pos[0 ].xyz, trianglePlane.xyz); if (dot(trianglePlane.xyz, vec3(0.0 , 0.0 , 1.0 )) < 0.0 ) { vec4 vertexTemp = pos[2 ]; pos[2 ] = pos[1 ]; pos[1 ] = vertexTemp; } if (trianglePlane.z == 0.0f ) return ; BoundingBox = calcAABB(pos, halfPixel[projectIndex]); vec3 edgePlanes[3 ]; edgePlanes[0 ] = cross(pos[0 ].xyw - pos[2 ].xyw, pos[2 ].xyw); edgePlanes[1 ] = cross(pos[1 ].xyw - pos[0 ].xyw, pos[0 ].xyw); edgePlanes[2 ] = cross(pos[2 ].xyw - pos[1 ].xyw, pos[1 ].xyw); edgePlanes[0 ].z -= dot(halfPixel[projectIndex], abs (edgePlanes[0 ].xy)); edgePlanes[1 ].z -= dot(halfPixel[projectIndex], abs (edgePlanes[1 ].xy)); edgePlanes[2 ].z -= dot(halfPixel[projectIndex], abs (edgePlanes[2 ].xy)); vec3 intersection[3 ]; intersection[0 ] = cross(edgePlanes[0 ], edgePlanes[1 ]); intersection[1 ] = cross(edgePlanes[1 ], edgePlanes[2 ]); intersection[2 ] = cross(edgePlanes[2 ], edgePlanes[0 ]); intersection[0 ] /= intersection[0 ].z; intersection[1 ] /= intersection[1 ].z; intersection[2 ] /= intersection[2 ].z; float z[3 ]; z[0 ] = -(intersection[0 ].x * trianglePlane.x + intersection[0 ].y * trianglePlane.y + trianglePlane.w) / trianglePlane.z; z[1 ] = -(intersection[1 ].x * trianglePlane.x + intersection[1 ].y * trianglePlane.y + trianglePlane.w) / trianglePlane.z; z[2 ] = -(intersection[2 ].x * trianglePlane.x + intersection[2 ].y * trianglePlane.y + trianglePlane.w) / trianglePlane.z; pos[0 ].xyz = vec3(intersection[0 ].xy, z[0 ]); pos[1 ].xyz = vec3(intersection[1 ].xy, z[1 ]); pos[2 ].xyz = vec3(intersection[2 ].xy, z[2 ]); vec4 voxelPos; ProjectPos = pos[0 ].xyz; gl_Position = pos[0 ]; voxelPos = viewProjectInverse[projectIndex] * gl_Position; FragPos = voxelPos.xyz; EmitVertex(); ProjectPos = pos[1 ].xyz; gl_Position = pos[1 ]; voxelPos = viewProjectInverse[projectIndex] * gl_Position; FragPos = voxelPos.xyz; EmitVertex(); ProjectPos = pos[2 ].xyz; gl_Position = pos[2 ]; voxelPos = viewProjectInverse[projectIndex] * gl_Position; FragPos = voxelPos.xyz; EmitVertex(); EndPrimitive(); }
最后的最后,我们还需要在片元着色器剔除无关的片元,具体原因我已经在前面说了,如果不做这一步的剔除操作,将出现如下图12所示的情况。在片元着色器中,我们根据传入的三角形包围盒与当前的片元位置判断是否需要丢弃该片元。具体看下面代码的第19行、第20行。
图12 保守光栅化出现的边边角角
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #version 430 core in vec3 FragPos; in vec3 ProjectPos; in vec4 BoundingBox; layout (std430, binding = 0 ) buffer CountBuffer{ int cnts[]; }; uniform bool conservate; uniform float step; uniform vec3 boxMin; uniform vec3 resolution; out vec4 color; void main () if (ProjectPos.x < BoundingBox.x || ProjectPos.y < BoundingBox.y || ProjectPos.x > BoundingBox.z || ProjectPos.y > BoundingBox.w) discard; uint x = uint((FragPos.x - boxMin.x)/step); uint y = uint((FragPos.y - boxMin.y)/step); uint z = uint((FragPos.z - boxMin.z)/step); uint index = uint(y * (resolution.z * resolution.x) + z * resolution.x + x); atomicAdd(cnts[index], 1 ); color = vec4(0.0 ,1.0 ,0.0 ,1.0 ); }
最终,修复了孔洞的效果的如下图,可以看到,对比前面的图9,孔洞基本都被“补”上了。
图13 保守光栅化出现的边边角角
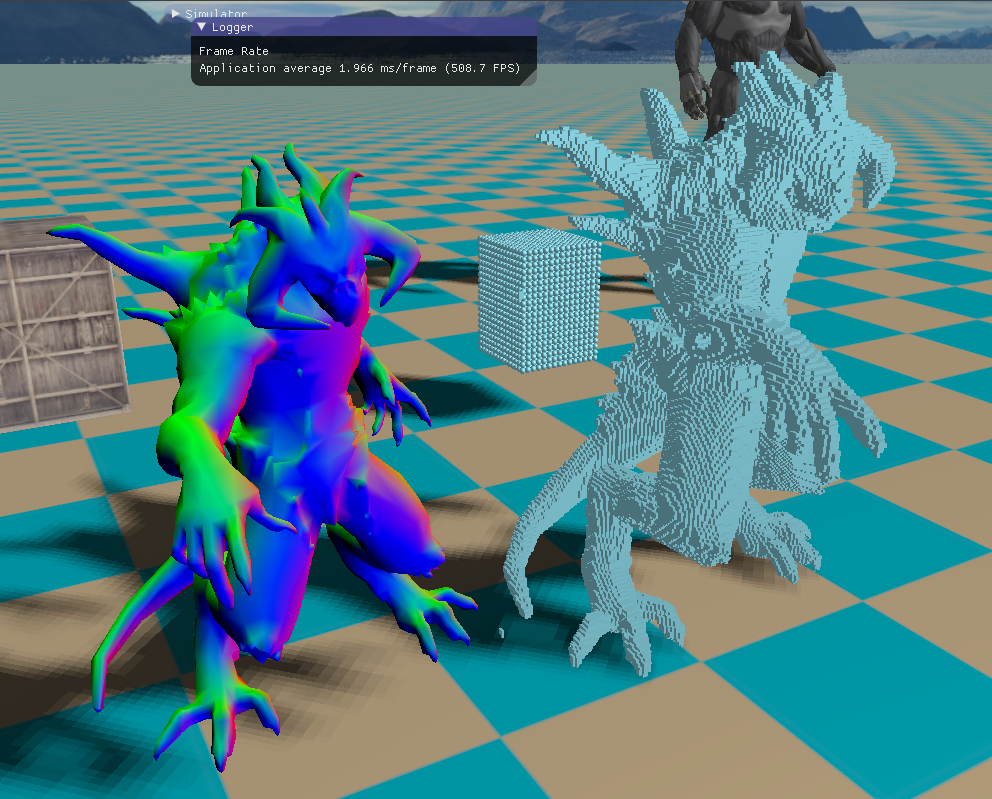
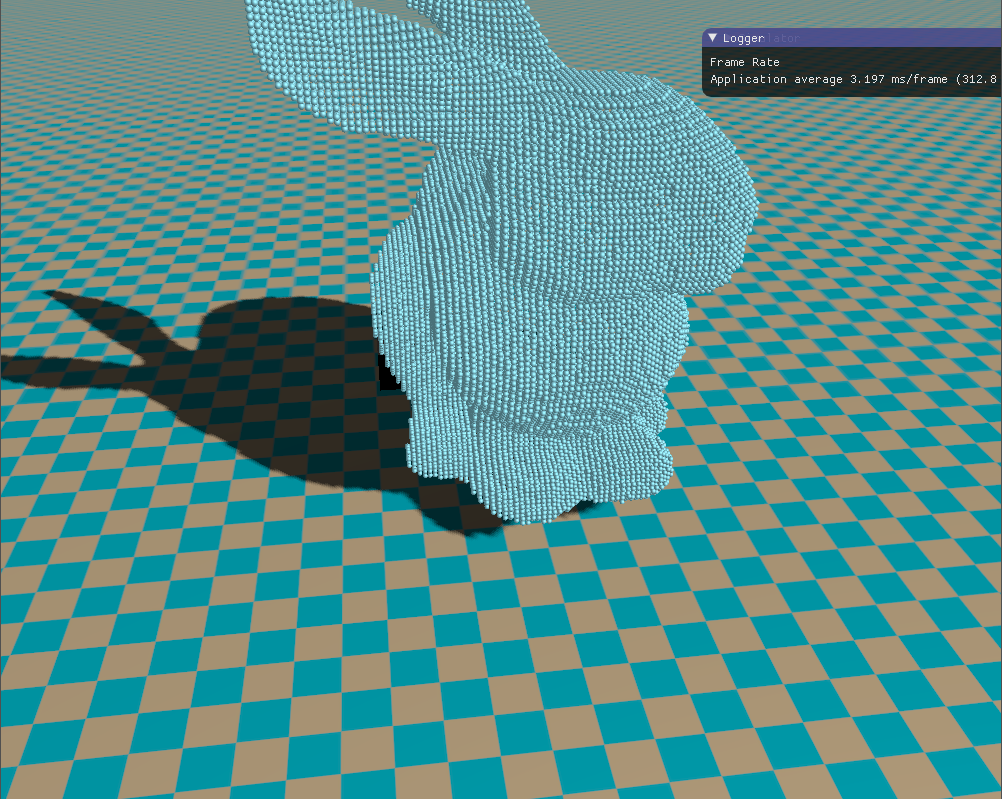
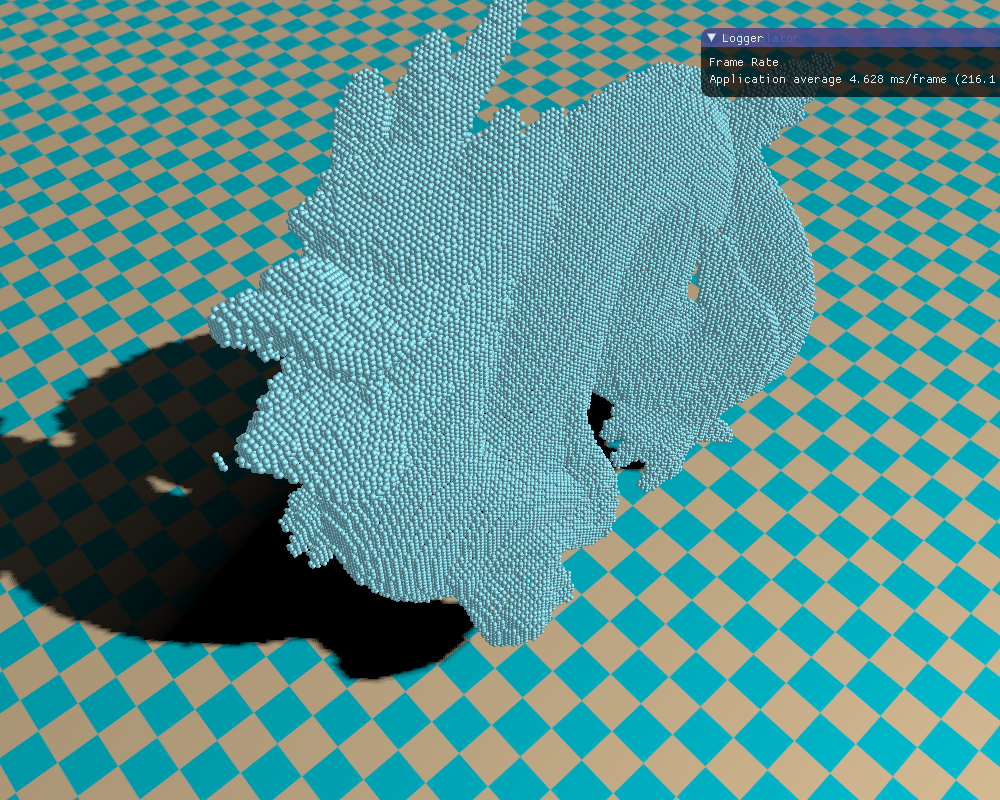
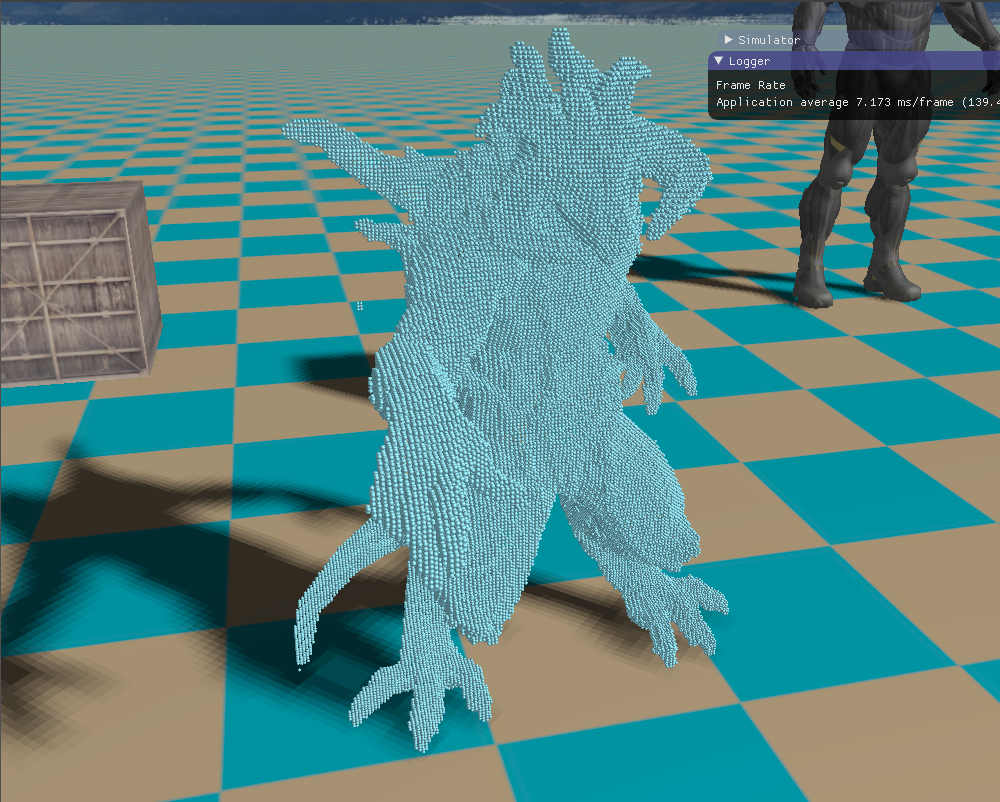
下面就是一些模型的体素化效果。
参考资料: $[1]$ The Basics of GPU Voxelization
$[2]$ 《GPU Gems 2》: Chapter 42. Conservative Rasterization
$[3]$ https://blog.csdn.net/xiewenzhao123/article/details/79875855