本章开始博主将手动搭建一个渲染管线，深入理解3D渲染的整个流程。线性代数中的向量和矩阵是计算机图形学的常客，深入理解和掌握对于图形渲染有着非常重要的意义，本节主要是关于3D数学库的内容。

  • 向量
  • 矩阵

一、向量

  $n$维向量本质就是一个$n$元组，从几何意义上来说，向量是有大小和方向的有向线段。向量的大小就是向量的长度（模）向量有非负的长度，而向量的方向描述了空间中向量的指向。向量的相关内容高中就已涉及，因此不再赘述。若想要重新深入了解相关内容，可以查看这个地址。

  图形渲染中通常使用的向量为$2$到$4$维，如下分别是$2$维、$3$维、$4$维向量类的常用方法，主要是运算操作符重载以及点乘、叉乘、模、标准化、线性插值等基本操作。向量的内容简单，没什么要特别说明的。

1、2D向量类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Vector2D
{
public:
    float x,y;

    // constructors
    Vector2D():x(0.0f), y(0.0f) {}
    Vector2D(float newX, float newY):x(newX), y(newY){}
    Vector2D(const float * rhs):x(*rhs), y((*rhs)+1) {}
    Vector2D(const Vector2D & rhs):x(rhs.x), y(rhs.y){}
    ~Vector2D() = default;

    // setter,getter
    void set(float newX, float newY){x=newX;y=newY;	}
    void setX(float newX) {x = newX;}
    void setY(float newY) {y = newY;}
    float getX() const {return x;}
    float getY() const {return y;}

    // normalization
    void normalize();
    Vector2D getNormalize()const;

    // length
    float getLength() const { return static_cast<float>(sqrt(x*x + y*y));}
    float getSquaredLength()const{return static_cast<float>(x*x + y*y);}

    // overloaded operators
    Vector2D operator+(const Vector2D &rhs) const {return Vector2D(x + rhs.x, y + rhs.y);}
    Vector2D operator-(const Vector2D &rhs) const {return Vector2D(x - rhs.x, y - rhs.y);}
    Vector2D operator*(const float rhs) const {return Vector2D(x*rhs, y*rhs);}
    Vector2D operator/(const float rhs) const {return (rhs==0) ? Vector2D(0.0f, 0.0f) : Vector2D(x / rhs, y / rhs);}

    bool operator==(const Vector2D &rhs) const {return (equal(x,rhs.x) && equal(y,rhs.y));}
    bool operator!=(const Vector2D &rhs) const {return !((*this)==rhs);}

    void operator+=(const Vector2D &rhs){x+=rhs.x;	y+=rhs.y;}
    void operator-=(const Vector2D &rhs){x-=rhs.x;	y-=rhs.y;}
    void operator*=(const float rhs){x*=rhs;y*=rhs;}
    void operator/=(const float rhs){if(!equal(rhs, 0.0)){x/=rhs;y/=rhs;}}

    Vector2D operator-() const {return Vector2D(-x, -y);}
    Vector2D operator+() const {return *this;}

    // interpolation
    Vector2D lerp(const Vector2D &v2,const float factor)const {return (*this)*(1.0f - factor) + v2*factor;}
    Vector2D quadraticInterpolate(const Vector2D & v2, const Vector2D & v3, const float factor) const
    {return (*this)*(1.0f-factor)*(1.0f-factor) + v2*2.0f*factor*(1.0f-factor) + v3*factor*factor;}

};

2、3D向量类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Vector3D
{
public:
    float x,y,z;

    // constructors
    Vector3D():x(0.0f), y(0.0f), z(0.0f){}
    Vector3D(float newX, float newY, float newZ):x(newX), y(newY), z(newZ){}
    Vector3D(const float * rhs):x(*rhs), y(*(rhs+1)), z(*(rhs+2)){}
    Vector3D(const Vector3D &rhs):x(rhs.x), y(rhs.y), z(rhs.z){}
    ~Vector3D() = default;

    // setter,getter
    void set(float newX, float newY, float newZ){x=newX;y=newY;z=newZ;}
    void setX(float newX) {x = newX;}
    void setY(float newY) {y = newY;}
    void setZ(float newZ) {z = newZ;}
    float getX() const {return x;}
    float getY() const {return y;}
    float getZ() const {return z;}

    // normalization
    void normalize();
    Vector3D getNormalized() const;

    // length caculation
    float getLength() const {return static_cast<float>(sqrt(x*x+y*y+z*z));}
    float getSquaredLength() const {return x*x+y*y+z*z;}

    // product
    float dotProduct(const Vector3D &rhs) const {return x*rhs.x + y*rhs.y + z*rhs.z;}
    Vector3D crossProduct(const Vector3D &rhs) const
    {return Vector3D(y*rhs.z - z*rhs.y, z*rhs.x - x*rhs.z, x*rhs.y - y*rhs.x);}

    // linear interpolation
    Vector3D lerp(const Vector3D &v2, float factor) const {return (*this)*(1.0f-factor) + v2*factor;}
    Vector3D QuadraticInterpolate(const Vector3D &v2, const Vector3D &v3, float factor) const
    {return (*this)*(1.0f-factor)*(1.0f-factor) + v2*2.0f*factor*(1.0f-factor) + v3*factor*factor;}

    // overloaded operators
    Vector3D operator+(const Vector3D &rhs) const {return Vector3D(x + rhs.x, y + rhs.y, z + rhs.z);}
    Vector3D operator-(const Vector3D &rhs) const {return Vector3D(x - rhs.x, y - rhs.y, z - rhs.z);}
    Vector3D operator*(const float rhs) const {return Vector3D(x*rhs, y*rhs, z*rhs);}
    Vector3D operator/(const float rhs) const {return (equal(rhs,0.0f))?Vector3D(0.0f, 0.0f, 0.0f):Vector3D(x/rhs, y/rhs, z/rhs);}

    bool operator==(const Vector3D &rhs) const {return (equal(x,rhs.x) && equal(y,rhs.y) && equal(z,rhs.z));}
    bool operator!=(const Vector3D &rhs) const {return !((*this)==rhs);}

    void operator+=(const Vector3D &rhs) {x+=rhs.x;y+=rhs.y;z+=rhs.z;}
    void operator-=(const Vector3D & rhs) {x-=rhs.x;y-=rhs.y;z-=rhs.z;}
    void operator*=(const float rhs){x*=rhs;y*=rhs;z*=rhs;}
    void operator/=(const float rhs){if(!equal(rhs,0.0f)){x/=rhs; y/=rhs; z/=rhs;}}

    Vector3D operator-() const {return Vector3D(-x, -y, -z);}
    Vector3D operator+() const {return *this;}
};

3、4D向量类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Vector4D
{
public:
    float x,y,z,w;

    // constructors
    Vector4D():x(0.0f), y(0.0f), z(0.0f), w(0.0f){}
    Vector4D(float newX, float newY, float newZ, float newW):x(newX), y(newY), z(newZ), w(newW){}
    Vector4D(const float * rhs):x(*rhs), y(*(rhs+1)), z(*(rhs+2)), w(*(rhs+3)){}
    Vector4D(const Vector4D &rhs):x(rhs.x), y(rhs.y), z(rhs.z), w(rhs.w){}
    Vector4D(const Vector3D & rhs):	x(rhs.x), y(rhs.y), z(rhs.z), w(1.0f){}
    ~Vector4D() = default;

    // setter,getter
    void set(float newX, float newY, float newZ, float newW){x=newX;y=newY;z=newZ;w=newW;}
    void setX(float newX) {x = newX;}
    void setY(float newY) {y = newY;}
    void setZ(float newZ) {z = newZ;}
    void setW(float newW) {w = newW;}
    float getX() const {return x;}
    float getY() const {return y;}
    float getZ() const {return z;}
    float getW() const {return w;}

    // product
    float dotProduct(const Vector4D &rhs) const {return x*rhs.x + y*rhs.y + z*rhs.z + w*rhs.w;}

    // linear interpolation
    Vector4D lerp(const Vector4D &v2, float factor) const {return (*this)*(1.0f-factor) + v2*factor;}
    Vector4D QuadraticInterpolate(const Vector4D &v2, const Vector4D &v3, float factor) const
    {return (*this)*(1.0f-factor)*(1.0f-factor)+v2*2.0f*factor*(1.0f-factor)+v3*factor*factor;}

    // overloaded operators
    Vector4D operator+(const Vector4D &rhs) const {return Vector4D(x+rhs.x, y+rhs.y, z+rhs.z, w+rhs.w);}
    Vector4D operator-(const Vector4D &rhs) const {return Vector4D(x-rhs.x, y-rhs.y, z-rhs.z, w-rhs.w);}
    Vector4D operator*(const float rhs) const {return Vector4D(x*rhs, y*rhs, z*rhs, w*rhs);}
    Vector4D operator/(const float rhs) const
    {return (equal(rhs,0.0f))?Vector4D(0.0f, 0.0f, 0.0f, 0.0f):Vector4D(x/rhs, y/rhs, z/rhs, w/rhs);}

    bool operator==(const Vector4D &rhs) const {return (equal(x,rhs.x)&&equal(y,rhs.y)&&equal(z,rhs.z)&&equal(w,rhs.w));}
    bool operator!=(const Vector4D &rhs) const {return !((*this)==rhs);}

    void operator+=(const Vector4D &rhs) {x+=rhs.x;y+=rhs.y;z+=rhs.z;w+=rhs.w;}
    void operator-=(const Vector4D & rhs) {x-=rhs.x;y-=rhs.y;z-=rhs.z;w-=rhs.w;}
    void operator*=(const float rhs){x*=rhs;y*=rhs;z*=rhs;w*=rhs;}
    void operator/=(const float rhs){if(!equal(rhs,0.0f)){x/=rhs; y/=rhs; z/=rhs; w/=rhs;}}

    Vector4D operator-() const {return Vector4D(-x, -y, -z, -w);}
    Vector4D operator+() const {return *this;}
};

二、矩阵

  矩阵本质就是向量的进一步扩展的，一个$n\times m$的矩阵可看成$n$个$m$维行向量组成或者$m$个$n$维列向量组成，关于矩阵的基本概念、操作请看这里。通常我们采用方阵来描述线性变换。所谓线性变换，即变换之后保留了直线而不被弯曲，平行线依然平行，原点没有变化，但其他的几何性质如长度、角度、面积和体积可能被变换改变了。直观来说，线性变换可能“拉伸”坐标系，但不会“弯曲”或“卷折”坐标系。

  矩阵在计算机中有行主序存储、列主序存储两种方式，行主序存储即按照顺序逐行存储，列主序存储则按照顺序逐列存储。图形学渲染中我们通常采用的是列主序的方式，以下的讨论都是列主序的矩阵存储方式。那么矩阵是如何变换向量的？

  向量在几何上能被解释成一系列与轴平行的位移，一般来说，任意向量$\vec v$都能写成如下的形式：

  公式$(1)$右边的单位向量就是$x$、$y$、$z$轴方向的向量，向量的每个坐标都表明了平行于相应坐标轴的有向位移。我们记$\vec p$、$\vec q$、$\vec r$分别为公式$(1)$中右边的$x$、$y$、$z$轴的单位列向量，则有：

  向量$\vec v$就变成了向量$\vec p$、$\vec q$、$\vec r$的线性表示，向量$\vec p$、$\vec q$、$\vec r$称作基向量。以上仅仅讨论的是笛卡尔坐标系，但更通用的情况是，一个$3$维坐标系能用任意$3$个线性无关的基向量表示，以列向量$\vec p$、$\vec q$、$\vec r$构建$3\times 3$的矩阵$M$：

  结合公式$(2)$和公式$(3)$，即有：

  坐标系变换矩阵的每一列（如果是行主序，就是每一行）都是该坐标系的基向量，一个点$v$右乘该矩阵就相当于执行了一次坐标系转换。求解线性变换矩阵的关键就是根据当前的坐标系求解变换之后的坐标系的基向量，然后将基向量填入向量位置！

  一个矩阵类通常有如下方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Matrix4x4
{
public:
    float entries[16];

    // constructors
    Matrix4x4(){loadIdentity();}
    Matrix4x4(float e0, float e1, float e2, float e3,
              float e4, float e5, float e6, float e7,
              float e8, float e9, float e10,float e11,
              float e12,float e13,float e14,float e15);
    Matrix4x4(const float *rhs);
    Matrix4x4(const Matrix4x4 &rhs);
    ~Matrix4x4() = default;

    // setter,getter
    void setEntry(int position, float value);
    float getEntry(int position) const;
    Vector4D getRow(int position) const;
    Vector4D getColumn(int position) const;
    void loadIdentity();
    void loadZero();

    // overloaded operators
    Matrix4x4 operator+(const Matrix4x4 & rhs) const;
    Matrix4x4 operator-(const Matrix4x4 & rhs) const;
    Matrix4x4 operator*(const Matrix4x4 & rhs) const;
    Matrix4x4 operator*(const float rhs) const;
    Matrix4x4 operator/(const float rhs) const;

    bool operator==(const Matrix4x4 & rhs) const;
    bool operator!=(const Matrix4x4 & rhs) const;

    void operator+=(const Matrix4x4 & rhs);
    void operator-=(const Matrix4x4 & rhs);
    void operator*=(const Matrix4x4 & rhs);
    void operator*=(const float rhs);
    void operator/=(const float rhs);

    Matrix4x4 operator-() const;
    Matrix4x4 operator+() const {return (*this);}
    Vector4D operator*(const Vector4D rhs) const;

    // inverse, transpose
    void inverted();
    Matrix4x4 getInverse() const;
    void transpose();
    Matrix4x4 getTranspose() const;
    void invertTranspose();
    Matrix4x4 getInverseTranspose() const;

    // operation on space
    void setTranslation(const Vector3D & translation);
    void setScale(const Vector3D & scaleFactor);
    void setRotationAxis(const double angle, const Vector3D & axis);
    void setRotationX(const double angle);
    void setRotationY(const double angle);
    void setRotationZ(const double angle);
    void setRotationEuler(const double angleX, const double angleY, const double angleZ);
    void setPerspective(float fovy, float aspect, float near, float far);
    void setPerspective(float left, float right, float bottom, float top, float near, float far);
    void setOrtho(float left, float right, float bottom, float top, float near, float far);
};

1、线性变换、仿射变换

  满足$F(a+b)=F(a)+F(b)$和$F(ka)=kF(a)$的映射$F(a)$就是线性的。对于映射$F(a)=Ma$，当$M$为任意方阵时，也可以说明$F$映射是一个线性变换。在计算机图形学中，缩放、旋转的变换操作都是线性的，但是平移不是线性变换。

  具有$v’=Mv’+b$形式的变换都是仿射变换。平移作为最常用的变换之一，然而却不是线性变换；所以为了包括平移变换提出了仿射变换。仿射变换是指线性变换后接着平移。因此，仿射变换的集合是线性变换的超集，任何线性变换都是仿射变换，但不是所有的仿射变换都是线性变换。为了统一用矩阵表示低维度的仿射变换，我们可以通过高维度的线性变换来完成，为此引入了$4$维齐次坐标。（当然引入第$4$维$w$还有其他的用途，如当$w=0$时，可解释为无穷远的“点”，其意义是描述方向）。

  从而，对于高维度来说只是经历了一次切变+投影变换就可以实现低维度的平移，在$3D$渲染中，我们采用$4\times 4$的矩阵做相应的变换。关于平移和缩放不再赘述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void Matrix4x4::setTranslation(const Vector3D &translation)
{
    loadIdentity();
    entries[12] = translation.x;
    entries[13] = translation.y;
    entries[14] = translation.z;
}

void Matrix4x4::setScale(const Vector3D &scaleFactor)
{
    loadIdentity();
    entries[0]  = scaleFactor.x;
    entries[5]  = scaleFactor.y;
    entries[10] = scaleFactor.z;
}

2、绕任意轴旋转

  在3D中，绕坐标轴旋转，而不是绕点旋转，此时首先需要定义的是何为旋转正方向： 左手坐标系中定义此方向的规则为左手法则。首先，要明确旋转轴指向哪个方向。当然，旋转轴在理论上是无限延伸的，但我们还是要认为它有正端点和负端点。与笛卡尔坐标轴定义坐标系相同，左手法则是这样的:伸出左手，大拇指向上，其余手指弯曲。大拇指指向旋转轴的正方向，此时，四指弯曲的方向就是旋转的正方向。右手坐标系则根据右手法则利用右手判断旋转正方向，本文讨论的是常见的右手坐标系。

  在旋转变换中，一个常见的特殊情况就是绕$x$轴、绕$y$轴、绕$z$轴旋转，这类的旋转矩阵求解比较简单，只需牢牢记住列主序矩阵的列向量就是变换后的坐标系的基向量即可快速推导出相应的旋转矩阵：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void Matrix4x4::setRotationX(const double angle)
{
    loadIdentity();
    entries[5]  =  static_cast<float>(cos(M_PI*angle/180));
    entries[6]  =  static_cast<float>(sin(M_PI*angle/180));
    entries[9]  = -entries[6];
    entries[10] =  entries[5];
}

void Matrix4x4::setRotationY(const double angle)
{
    loadIdentity();
    entries[0]  =  static_cast<float>(cos(M_PI*angle/180));
    entries[2]  = -static_cast<float>(sin(M_PI*angle/180));
    entries[8]  = -entries[2];
    entries[10] =  entries[0];
}

void Matrix4x4::setRotationZ(const double angle)
{
    loadIdentity();
    entries[0]  =  static_cast<float>(cos(M_PI*angle/180));
    entries[1]  =  static_cast<float>(sin(M_PI*angle/180));
    entries[4]  = -entries[1];
    entries[5]  =  entries[0];
}

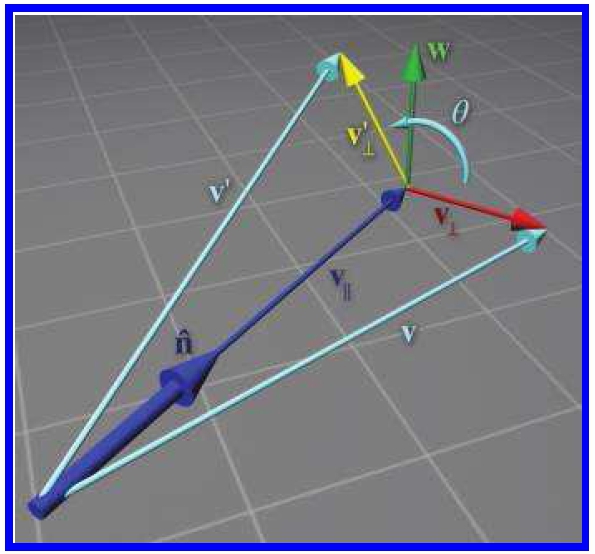
  但是更一般的情况是绕任意轴进行旋转，构建这样的矩阵稍微有点麻烦，我们接下来就做一些绕任意轴旋转的矩阵构建推到。在这里我们不考虑平移，因而围绕旋转的轴一定是通过原点的。如下图1所示，将$\vec v$旋转到$\vec v ‘$，任意轴用单位向量$\vec n$表示，绕$\vec n$旋转$\theta$角度的矩阵记为$R(\vec n, \theta)$，$\vec v’$是向量绕轴$\vec n$旋转后的向量，即$\vec v’=R(\vec n,\theta)\vec v$。

图1 绕任意轴旋转

  我们的目标就是用$\vec v$、$\vec n$和$\theta$来表示$\vec v’$，从而构造出$R(\vec n, \theta)$。首先将$\vec v$分解成平行于$\vec n$的向量$\vec v_{||}$和垂直于$\vec n$的分量$\vec v_{⊥}$，而$\vec v’_{⊥}$是垂直于$\vec n$的分向量。注意，$\vec n$是单位向量，但$\vec v$不是单位向量，可得$\vec v$在$\vec n$方向的投影向量$\vec v_{||}$为：

  从而根据$\vec v_{||}$和$\vec v$可知$\vec v_{⊥}$和$w$，$w$是垂直于$\vec n$和$\vec v_{⊥}$的向量：

  $\vec w$和$\vec v_{⊥}$相互垂直，$\vec w$、$\vec v_{⊥}$和$\vec v’_{⊥}$在同一个平面上，$\vec v’_{⊥}$和$\vec v_{⊥}$的夹角为$\theta$，从而$\vec v’_{⊥}$可由$\vec w$和$\vec v_{⊥}$线性表示为：

  最后，根据公式$(6)$和公式$(9)$我们已知$\vec v_{||}$和$\vec v’_{⊥}$，从而可以得出$\vec v’$：

  由公式$(10)$可知，我们已经用$\vec v$、$\vec n$和$\theta$表示$\vec v’$，那如何根据上述的公式$(10)$构建旋转矩阵$R(\vec n, \theta)$？还是那个思路：列主序变换矩阵的列向量就是变换后的坐标系的基向量。我们只需求出笛卡尔坐标系的$\vec x$、$\vec y$、$\vec z$三个轴方向上的基向量按照公式$(10)$旋转之后的基向量$\vec x’$、$\vec y’$、$\vec z’$，然后填入矩阵$R(\vec n, \theta)$即可，以$\vec x=[1\ \ 0 \ \ 0]^T$为例：

  $\vec y=[0\ \ 1\ \ 0]^T$和$\vec z=[0\ \ 0\ \ 1]^T$同理：

  将$\vec x’$、$\vec y’$、$\vec z’$合并到$R(\vec n, \theta)$中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void Matrix4x4::setRotationAxis(const double angle, const Vector3D &axis)
{
    Vector3D u = axis.getNormalized();

    float sinAngle = static_cast<float>(sin(M_PI*angle/180));
    float cosAngle = static_cast<float>(cos(M_PI*angle/180));
    float oneMinusCosAngle = 1.0f - cosAngle;

    loadIdentity();

    entries[0]  = (u.x)*(u.x) + cosAngle*(1-(u.x)*(u.x));
    entries[4]  = (u.x)*(u.y)*(oneMinusCosAngle) - sinAngle*u.z;
    entries[8]  = (u.x)*(u.z)*(oneMinusCosAngle) + sinAngle*u.y;

    entries[1]  = (u.x)*(u.y)*(oneMinusCosAngle) + sinAngle*u.z;
    entries[5]  = (u.y)*(u.y) + cosAngle*(1-(u.y)*(u.y));
    entries[9]  = (u.y)*(u.z)*(oneMinusCosAngle) - sinAngle*u.x;

    entries[2]  = (u.x)*(u.z)*(oneMinusCosAngle) - sinAngle*u.y;
    entries[6]  = (u.y)*(u.z)*(oneMinusCosAngle) + sinAngle*u.x;
    entries[10] = (u.z)*(u.z) + cosAngle*(1-(u.z)*(u.z));
}

3、透视投影、正交投影

  $3D$空间中的物体最终都要通过投影显示到$2D$的屏幕上，这一过程就是投影变换。投影变换矩阵将视图空间中的顶点数据变换到裁剪空间，裁剪空间中的顶点最后通过透视除法被变换到标准化设备坐标（$NDC$）。通常由两类投影：透视投影、正交投影。

透视投影矩阵

  关于透视投影矩阵的前世今生我不过多说，直接上透视投影矩阵的推导过程。一个视锥体我们目前用六个参数表示：$left$，$right$，$bottom$，$top$，$near$，$far$，简写为$l$、$r$、$b$、$t$、$n$和$f$，即视锥体的六个面。我们的目标就是将视图空间中在视锥体内的点变换到标准化设备坐标中的立方体内。即$x$轴方向从$[l,r]$映射到$[-1,1]$，$y$轴方向从$[b,t]$映射到$[-1,1]$，$z$轴方向从$[-n,-f]$映射到$[-1,1]$。

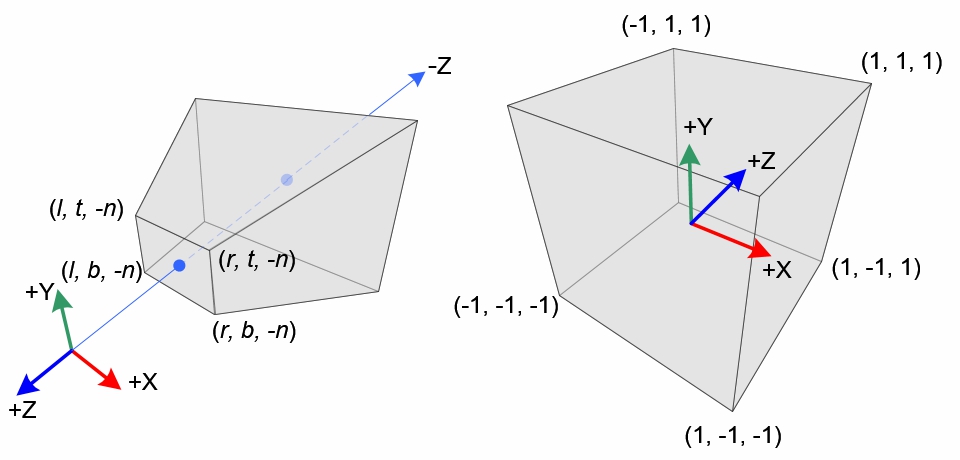
  可能你会觉得奇怪，$z$轴方向为什么是从$[-n,-f]$映射到$[-1,1]$？这是因为摄像机空间的坐标系是右手坐标系，在视图空间中摄像机是朝向视图坐标系的$z$轴的负方向，如下图左边所示，$+Y$、$+Z$、$+X$标准摄像机坐标系的三个轴，而摄像机的观察视锥体是朝向$-Z$方向的。而$NDC$又是左手坐标系，朝向$+Z$方向，所以我们要取负。

图2 透视投影视锥和标准化设备坐标

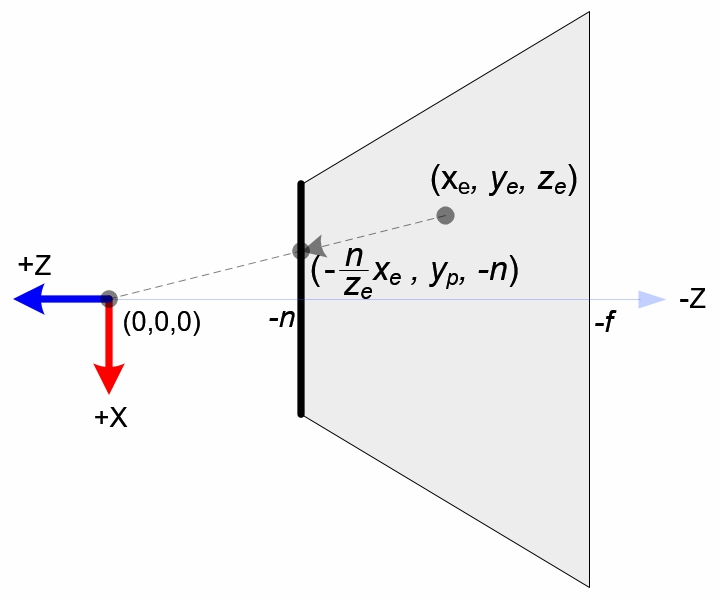
图3 从-Y方向看去的视锥横截面

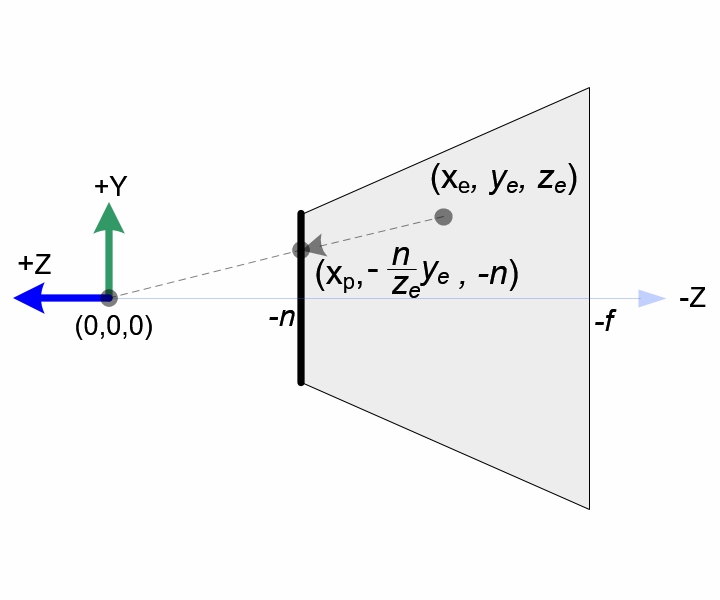
图4 从-X方向看去的视锥横截面

  在视锥体中的顶点$(x_e,y_e,z_e)$被投影到视锥体的近平面，近平面上的点我们记为$(x_p,y_p,-n)$。如图3和图4所示，根据三角形相似的原理，我们有：

  注意到公式$(15)$和$(16)$中分母都是一个$-z_e$，这与我们将裁剪空间中的顶点做透视除法相对应，透视投影然后做透视除法如下公式$(17)$、$(18)$所示：

  为了便于构建矩阵（$x_e$和$y_e$均与$-z_e$相除，不好构建矩阵），我们令裁剪空间中的$w_{clip}$为$-z_e$，将除以$-z_e$的这一步挪到了透视除法去做。故目前的透视矩阵就变为：

  其中”$.$”均表示未知。得到在近平面的$x_p$和$y_p$之后，我们还要将$x_p$映射到$[-1,1]$范围，同理$y_p$也是。以$x_p$为例，我们知道其值域为$[l,r]$。为了将$x_p$其映射到$[-1,1]$，我们首先将其映射到$[0,1]$，不难得到如下式子：

  式$(20)$乘上一个$2$再减去$1$就映射到了$[-1,1]$，映射之后记为$x_n$：

  同理$y_p$到$y_n$的映射：

  然后将公式$(15)$中的$x_p$带入公式$(21)$，将公式$(16)$中的$y_p$带入公式$(22)$，以$x_p$为例：

  其中$x_c$即公式$(19)$中的裁剪空间中的$x$轴坐标值。$y_p$同理可得$y_c$:

  现在我们已经知道了$x_c$和$y_c$分辨关于$x_e$、$y_e$以及$z_e$的表达形式，我们可以填充式$(19)$中的投影矩阵第一行与第二行：

  现在我们还剩下投影矩阵的第三行还不知道。因为我们知道$z$的投影与$x_e$和$y_e$无关，只与$z_e$、$w_e$有关，故可以假设投影矩阵的第三行如上式$(25)$所示，$A$和$B$就是我们假设的要求解的未知表达式。此外，在视图空间中的$w_e$是等于$1$的，$w_c$即前面提到的$-z_e$，从而有：

  为了求出公式$(26)$中的$A$和$B$，我们取两个极端的例子：在$-n$处的$z$值被映射到$-1$，在$-f$处的$z$值被映射到$1$，将$(z_n,z_e)=(-1,-n)$和$(z_n,z_e)=(1,-f)$带入式$(26)$中，可得方程组：

  求解方程$(27)$，可得$A$与$B$如下所示：

  将公式$(28)$带入公式$(26)$中：

  我们最终得到了$z_c$关于$z_e$的表达式，将$A$与$B$填入式$(25)$的投影矩阵即可，$M_{projection}$就是我们一直在寻求的透视投影矩阵：

  公式$(30)$中的透视投影矩阵只是一个通用的形式，在视图空间中的视锥体通常都是关于$x$轴和$y$轴对称的，从而有$r=-l$、$t=-b$，将式$(30)$简化成如下形式：

   但是通常我们传入构建透视矩阵函数的参数是$fovy$（$y$轴方向的视域角）、$aspect$（屏幕的宽高比）、$near$（近平面）以及$far$（远平面），如何根据这些参数构造式$(31)$的透视投影矩阵呢？注意到$r-l=width$即近平面宽度，$t-b=height$即近平面的高度，我们可以根据$fovy$和$aspect$得出$width$和$height$，具体细节不再赘述：

1
2
3
4
5
6
7
8
9
10
11
12
void Matrix4x4::setPerspective(float fovy, float aspect, float near, float far)
{
    loadZero();
    // convert fov from degrees to radians
    float rFovy = fovy*M_PI/180;
    const float tanHalfFovy = tanf(static_cast<float>(rFovy*0.5f));
    entries[0]         = 1.0f/(aspect*tanHalfFovy);
    entries[5]         = 1.0f/(tanHalfFovy);
    entries[10]        = -(far+near)/(far-near);
    entries[11]        = -1.0f;
    entries[14]        = (-2.0f*near*far)/(far-near);
}

正交投影矩阵

  理解了透视投影矩阵的构造之后，正交投影就简单太多了，正交投影只需做简单的线性映射就行了。只需将$x$轴方向从$[l,r]$映射到$[-1,1]$，$y$轴方向从$[b,t]$映射到$[-1,1]$，$z$轴方向从$[-n,-f]$映射到$[-1,1]$，而这个映射的过程很简单，正如前面公式$(20)$和$(21)$那样，先映射到$[0,1]$，再映射到$[0,2]$，最后映射到$[-1,1]$，这个过程我也不细说了，直接上结果：

  然后又因为视锥体关于$x$轴、$y$轴对称，简化的正交投影矩阵就为：

1
2
3
4
5
6
7
8
9
10
void Matrix4x4::setOrtho(float left, float right, float bottom, float top, float near, float far)
{
    loadIdentity();
    entries[0]     =  2.0f/(right-left);
    entries[5]     =  2.0f/(top-bottom);
    entries[10]    = -2.0f/(far-near);
    entries[12]    = -(right+left)/(right-left);
    entries[13]    = -(top+bottom)/(top-bottom);
    entries[14]    = -(far+near)/(far-near);
}

4、lookAt函数构造视图矩阵

  视图矩阵的工作目标是将世界坐标系中的所有物体的顶点的坐标从世界坐标系转换到摄像机坐标系。这是因为摄像机坐标系的原点不一定与世界坐标系重合，同时由于自身的旋转，坐标轴也一定不与世界坐标系的坐标轴平行。为完成工作任务，需要分为两步走：首先整体平移，将摄像机平移至世界坐标系原点，然后将顶点从世界坐标系变换至摄像机坐标系。

  lookAt函数的输入参数分别为：$eye$摄像机的位置，$target$摄像机目标点，$up$世界空间的上向量,。首先我们要根据这些参数确定摄像机坐标系的三个轴向量，其中需要非常注意的就是变换到视图空间中时摄像机是朝向视图空间的$-Z$方向的，所以求视图空间中的$Z$轴时是摄像机的位置减去目标点的位置：

  通过以上的方式我们就求出了视图空间的三条轴向量，再加上摄像机的位置我们就可以求出将世界坐标变换到与视图坐标重合的矩阵了，记为$M=T\cdot R$，其中$T$是平移到摄像机位置$eye$的变换矩阵，$R$是旋转到摄像机坐标轴方向的旋转矩阵：

  然而公式$(34)$并不是我们要求的视图矩阵，上式中的矩阵$M$仅仅是将世界坐标轴变换到摄像机坐标轴。摄像机只是一个虚拟的物品，我们不能将上述的矩阵$M$作用于摄像机，因为摄像机根本不存在！我们视图矩阵最终作用的世界空间中的物体，这就涉及到了一个相对运动的概念！

  当我们向前移动摄像机的时候，可以看成是摄像机不动，而物体朝着与摄像机朝向相反的方向移动。当我们向右旋转摄像机时，相当于摄像机不动而物体朝着摄像机的左边移动。摄像机的构造得益于相对于运动的理论，计算机图形学中的虚拟$3D$摄像机实际上是通过物体的移动来实现的，所以我们要构造的视图矩阵是公式$(34)$中的逆矩阵。

  由上式可知，构造视图矩阵涉及到$R$和$T$的求逆，其中的平移矩阵$T$的求逆则是直接取平移量的相反数即可：

  至于旋转矩阵$R$，我们知道旋转矩阵都是正交矩阵，正交矩阵的一个特点就是它的逆等于它的转置：

  最后，我们得到视图矩阵：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void Matrix4x4::setLookAt(Vector3D cameraPos, Vector3D target, Vector3D worldUp)
{
    Vector3D zAxis = cameraPos - target;
    zAxis.normalize();
    Vector3D xAxis = worldUp.crossProduct(zAxis);
    xAxis.normalize();
    Vector3D yAxis = zAxis.crossProduct(xAxis);
    yAxis.normalize();

    loadIdentity();
    entries[0] = xAxis.x;
    entries[4] = xAxis.y;
    entries[8] = xAxis.z;

    entries[1] = yAxis.x;
    entries[5] = yAxis.y;
    entries[9] = yAxis.z;

    entries[2] = zAxis.x;
    entries[6] = zAxis.y;
    entries[10] = zAxis.z;

    entries[12] = -(xAxis.dotProduct(cameraPos));
    entries[13] = -(yAxis.dotProduct(cameraPos));
    entries[14] = -(zAxis.dotProduct(cameraPos));
}

参考资料

$[1]$ http://www.songho.ca/opengl/gl_projectionmatrix.html

$[2]$ https://blog.csdn.net/zsq306650083/article/details/8773996

$[3]$ https://blog.csdn.net/y1196645376/article/details/78463248

$[4]$ https://www.cnblogs.com/J1ac/p/9340622.html

$[5]$ https://learnopengl-cn.github.io/01%20Getting%20started/08%20Coordinate%20Systems/

 上一页

Computer Graphics Soft Renderer Rasterization

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 ， 总访问量为 次 。
载入天数...载入时分秒...