高质量实时渲染：实时光线追踪

本文是闫令琪老师GAMES202高质量实时渲染课程的学习笔记和总结，本次主题是该课程的最后一部分内容——实时光线追踪，这方面的内容主要是关于低采样率下实时光线追踪的时间域降噪算法和空间域降噪算法。

  在计算机图形学领域，光线追踪算法是渲染的核心算法，但因其耗时长、计算量大等致命的性能缺陷一直不被实时渲染领域采纳（最多仅用于离线烘焙阶段）。自2018年NVIDIA正式发布了图灵架构的RTX硬件光追显卡起，实时渲染领域才算正式迈出了实时光追（Real-time Ray Tracing，简称RTRT）从零到一的关键一步。对于越来越追求极致渲染的当下来说，实时光线追踪才是未来。

一、实时光线追踪

  实时光线追踪并没有新的算法理论内容，它本质上就是离线渲染领域已经发展得非常成熟的路径追踪光路传输算法，并在此基础上做了简化。因此本文这里不会再对路径追踪的算法原理进行赘述。

图1 RTX实时光追

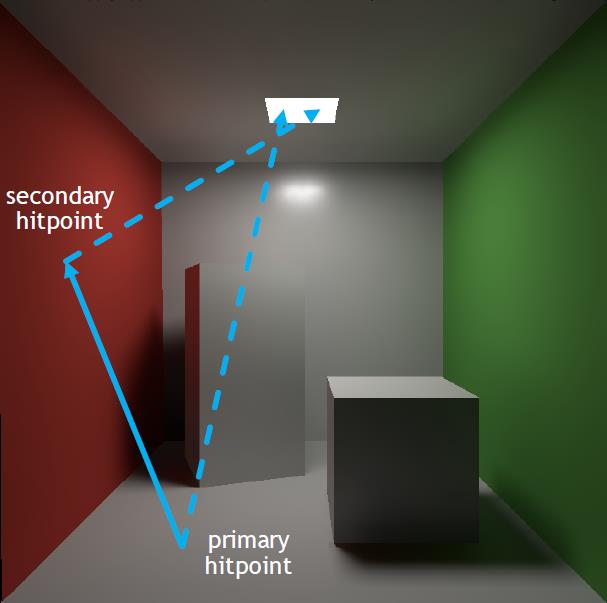
  RTX实时光追实际上只做了至多弹射两次的光路追踪。如上图1所示，有两个弹射点。第一个点是射线从摄像机出发打到场景中交点，称之为primary hitpoint；第二个点是从primary hitpoint出发投射追踪光线击中的点，称之为secondary hitpoint。这两个点就是RTX实时光追的路径追踪点。

  目前显卡为每个像素分配的采样点数为1（即1 Sample Per Pixel，简称1SPP），因此概括起来RTX实时光追做的其实就是1 SPP的Path Tracing，其追踪的路径包含：1 rasterization（primary）+ 1 ray（primary visibility） + 1 ray（secondary bounce） + 1 ray（secondary visibility）。

  其中visibility是Shadow Ray，用于计算采样点到光源之间的可见性。primary hitpoint不需要像离线渲染那样投射光线找到当前像素对应的世界空间下的交点，而是可以直接通过光栅化得到。综合来看，目前RTX实时光追还是非常简陋的，无论是采样数量还是采样路径长度都远远不够（低到令人发指），这种程度的光追必然会产生非常明显的噪声点，正如下图2所示。

图2 1SPP RTX实时光追的渲染结果

  因此，当前的实时光追最为关键的反而不是光追算法本身，而是降噪算法，其目的是通过降噪技术来消除渲染结果中的噪声点，使得渲染的结果真正能为人眼所接受。当然引入降噪算法同样需要考量降噪带来的额外性能开销，实时渲染对此有非常严格和明确的性能要求（例如<2ms），因此很多计算量大的降噪算法都被直接被Pass了。目前的实时降噪算法主要从时间域和空间域两个方面展开，以下是这两方面降噪算法的一个简述。

二、时间域（Temporal）降噪算法

  降噪的终极方法就是增大采样率，根据奈奎斯特定理可知，当采样频率高于信号最高频率的两倍时，采样的信号能够完美地重建出原始信号。但这样带来的代价就是计算性能急剧下降（离线渲染都不敢设置太高的SPP数，因为计算量实在太大了）。时间域降噪算法本质上也是期望增大每个像素的SPP数，但是它并非直接暴力地在空间中增大采样数，而是把目光投向渲染帧之间的时间轴。

  时间域降噪算法基于以下的核心思路：

• 前一帧已经被降噪好了，并且可以被复用；
• 通过运动矢量（motion vectors）找到当前帧的像素点对应到上一帧所在的位置
• 通过时间轴的累积来隐式地增大采样SPP数。

  寻找第$i$帧的像素$x$在第$i-1$帧的世界空间位置，我们称之为后向投影（Back Projection）。后向投影可以分成如下的几个步骤：

• 获取像素$x$的世界空间坐标点$s$，如果有G-buffer，那么可以直接根据像素坐标$x$获取其世界坐标$s$；而如果没有G-buffer，则可以通过逆向变换得到$s$，即有$s=V^{-1}P^{-1}E^{-1}x$，$E$是视口变换矩阵，$x$包含深度值$z$。
• 设前一帧$s$点在$s^{prev}$处，若物体没有在世界空间移动，那么motion vector就是零向量；而若物体移动了，设变换矩阵为$T$（即$s=Ts^{prev}$），则有$s^{prev}=T^{-1}s$；
• 最后把前一帧的$s^{prev}$通过前一帧的MVP矩阵投影回屏幕空间，得到$x^{prev}=P^{prev}V^{prev}s^{prev}$，从而得到$x$对应前一帧所在的屏幕位置$x^{prev}$。

  通过上述的后向投影就可以找到前一帧的采样值$C^{(i-1)}$，然后以一定的权重$\alpha$将其与当前帧的采样值$C^{(i)}$进行线性混合，从而得到时间域滤波的结果。即滤波后的结果为$\overline C$，未滤波的结果为$\tilde C$。在时间域滤波之前，通常会对其进行空间域的滤波

$$\overline C^{(i)}=Filter[\tilde C^{(i)}]$$

  最终的滤波结果为：

$$\overline C^{(i)}=\alpha \overline C^{(i)}+(1-\alpha)C^{(i-1)}$$

  滤波混合权重通常取$0.1-0.2$，即$80\%$到$90\%$的滤波值来源于前一帧的结果。这种基于时间域的降噪采样方法计算量小、性能高效，而且滤波的结果非常令人惊艳，下图3给出了前面图2的降噪结果，可以看到，降噪滤波后的渲染结果显得非常明亮干净。

图3 前面图2的时间域滤波降噪结果

  当然，这种依赖于时间轴连续帧的降噪算法也有自己的弱点，当后向投影超出屏幕空间之外时，也就是说当前帧的内容上一帧还没有，这个时候算法就尴尬了。这个弱点通常暴露在以下三个常见的场景：

• 渲染场景的瞬间切换，即相邻两帧之间渲染了完全不同的内容；
• 在一个狭长通道（例如走廊），镜头不断往后移动，画面不断涌现通道两边的新内容；
• 背景原先被遮挡的地方突然出现（例如前景物体突然消失或光速飞走）。

  后向投影超出屏幕之外直接不进行时域滤波处理。而对于未超出屏幕之外的情况，如果不对上述的情况做进一步的处理，那么就会出现明显的Artifact——拖影现象（Lagging）。这种拖影现象不仅会出现在场景中移动的物体上，而且也会出现在光照着色发生变化的地方（例如场景中的光源发生了变化，那么场景不同区域的阴影、光照反射均会发生变化，这些变化也会产生拖影现象）。

  一种解决拖影现象的方案是基于物体检测的方法。对于场景中的物体，我们都给他一个ID值（这个ID信息可以通过光栅化映射到每个像素上），在后向投影时通过比较当前帧当前像素的ID与上一帧像素的ID是否一致来判断是否投影到了其他区域上。如果不一致，那么就可以对混合权重$\alpha$进行调整（相应地增大空间域滤波的比重），但这种方法会在相应的区域重新引入噪声。

三、空间域（Spatial）降噪算法

  噪声在图像中通常表现为高频信号（或亮或暗），因此降噪算法本质上就是设计一个低通滤波器（low-pass filter）来去除这些高频噪声。我们记噪声图像为$\tilde C$，空间域滤波核为$K$（滤波核并非一定要固定不变，可针对每个像素使用不同的滤波核），滤波降噪后的图像为$\overline C$。

  空间域滤波本质就是卷积，即对每个像素的周围邻域的像素做一个加权平均的过程，非常简单（伪代码如下所示）。权重之和sum_of_weights是为了最后的归一化，防止能量不守恒。

For each pixel i
	sum_of_weights = sum_of_weighted_values = 0.0
	For each pixel j around i
		Calculate the weight w_ij = G(|i - j|, sigma)
		sum_of_weighted_values += w_ij * C^{input}[j]
		sum_of_weights += w_ij
	C^{output}[I] = sum_of_weighted_values / sum_of_weights

  在低通滤波器中，传统的高斯滤波器是一种常见的滤波器。虽然能够显著地去除高频噪声，但该滤波器带来的过度模糊的效应使得其在降噪领域并不是太受欢迎。对于高频的信号，高斯滤波器一视同仁，导致滤波的结果亦丢失了其他非噪声的高频信息，表现为图像中的物体边界被平滑掉了。

  相比之下，一种更为好用的降噪滤波器是双边滤波器（Bilateral filtering）。不难观察到，物体的边界处颜色会产生剧烈的变化。为了保持边界，双边滤波器利用了这个信息。双边滤波器的滤波核计算公式为：

$$w(i,j,k,l)=\exp (-\frac{(i-k)^2+(j-l)^2}{2\sigma^2_d}-\frac{||I(i,j)-I(k,l)||^2}{2\sigma^2_r})$$

  其中，$(i,j)$是滤波中心坐标，$(k,l)$是邻域像素坐标，$I(i,j)$是指$(i,j)$处的像素取值。可以看到，双边滤波器综合考虑了像素坐标的空间距离和像素颜色的差距，比高斯滤波器考虑了更多的因素，这也正是双边滤波器能够滤波保边的原因。下图4给出了双边滤波的滤波效果对比，滤波后图像中物体的边缘能够保持得非常不错。

图4 双边滤波前后对比

  无论是高斯滤波器还是双边滤波器，他们都是一种纯粹的图像处理方法。其中高斯滤波器考虑了像素坐标的空间距离，双边滤波器在此基础上进一步引入了像素颜色差距的考量指标（metric），使得降噪的效果更上一层。受此启发，我们可以利用更多的因素来设计更好的降噪滤波核。图形渲染比之于图像处理，其最大的不同就是图形渲染是已知物体的三维空间信息的，因此一种利用更多三维信息的滤波器——联合双边滤波器（Joint/Cross Bilateral filtering）被提出并应用到路径追踪渲染的降噪实现中。

  所谓的联合双边滤波器，其实就是在双边滤波器的基础上，引入了更多的考量指标，这些指标包括法线向量、深度值、世界空间坐标甚至物体表面的Albeo等三维几何信息。在图形渲染中，这些三维几何信息可以很容易地通过光栅化的方式获取，然后用G-buffer将这些信息缓存下来，需要时可以直接根据像素坐标进行读取。这是图形渲染特有的优势！而且值得一提的是，这些G-buffer信息本身不会有任何噪声点，因此可以放心地使用。

  联合双边滤波器不难理解。例如深度值指标，我们可以在滤波器公式中加入两个像素之间的深度值差异来使得滤波核在深度变化剧烈的地方取值较小（因为深度差异大意味着很有可能这两个像素在不同的物体上，因此为了保持边缘，需要消减滤波权重）。其他的考量指标例如法线向量（法线向量的差异可以通过点乘来度量）、物体Albeo等亦是以类似的方式融入到滤波核公式中。

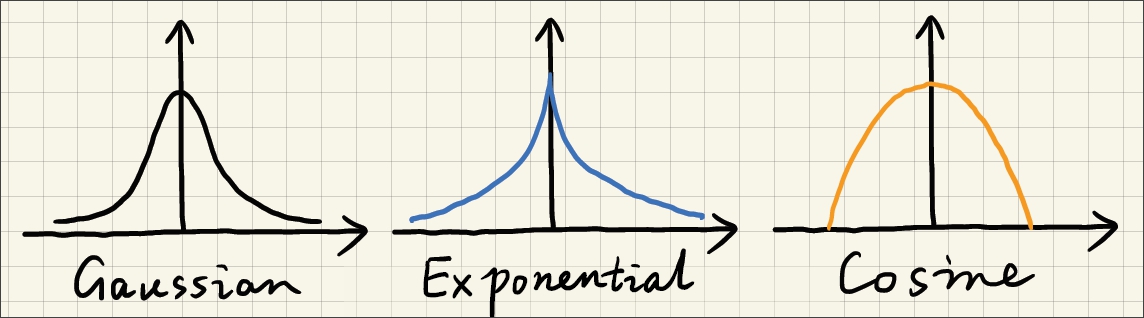
  值得注意的是，高斯形状的滤波核分布并非是唯一的选择，类似的指数分布和余弦分布也是可选的分布函数。他们的区别在于中心向周围过渡时的变化剧烈程度，指数分布变化剧烈，而余弦分布变化较缓。关于联合双边滤波器的更多细节可移步到参考资料$^{[1]}$。

  滤波通常需要对周围邻域的纹素进行采样，采样的数量取决于滤波核的大小。纹理采样是一个非常耗时的操作，因此对于大滤波器，实时渲染领域通常会用一些技巧来降低滤波所需的纹理采样数量。一种技巧就是将二维的滤波拆分为两个一维的滤波过程，从而使得滤波采样的数量从$N^2$降低到$2N$（其中$N$是滤波核大小）。以高斯滤波器为例，一个二维的高斯滤波器可以被拆分成水平方向和垂直方向的一维高斯滤波器：

$$G_{2D}(x,y)=G_{1D}(x)\cdot G_{1D}(y)$$

  上述公式成立是因为：

$$\int \int F(x_0,y_0)G_{2D}(x_0-x,y_0-y)dxdy =\int(\int F(x_0,y_0)G_{1D}(x_0-x)dx)G_{1D}(y_0-y)dy$$

  即高斯滤波器是可拆分的，左右两边是完全等价的。但对于双边滤波器，理论上其并没有可拆分的良好性质，但实际上工业界会强行拆分从而提升滤波效率，强行拆分的代价就是产生了一些Artifacts。这些Artifacts一定程度上可以接受，这种trade-off技巧在工业界很常见。

  除了二维拆分成一维的方法，另一种技巧就是以固定大小的滤波器多次滤波、依次逐渐增大滤波器的滤波范围来实现超大滤波器的滤波过程。例如，假设我们固定滤波器大小为$5\times 5$，而真正想要实现的滤波范围是$64\times 64$，那么用$5\times 5$大小的滤波器滤波$5$次，每次滤波采样之间间隔为$2^i$（其中$i$是迭代次数，从$0$开始）。

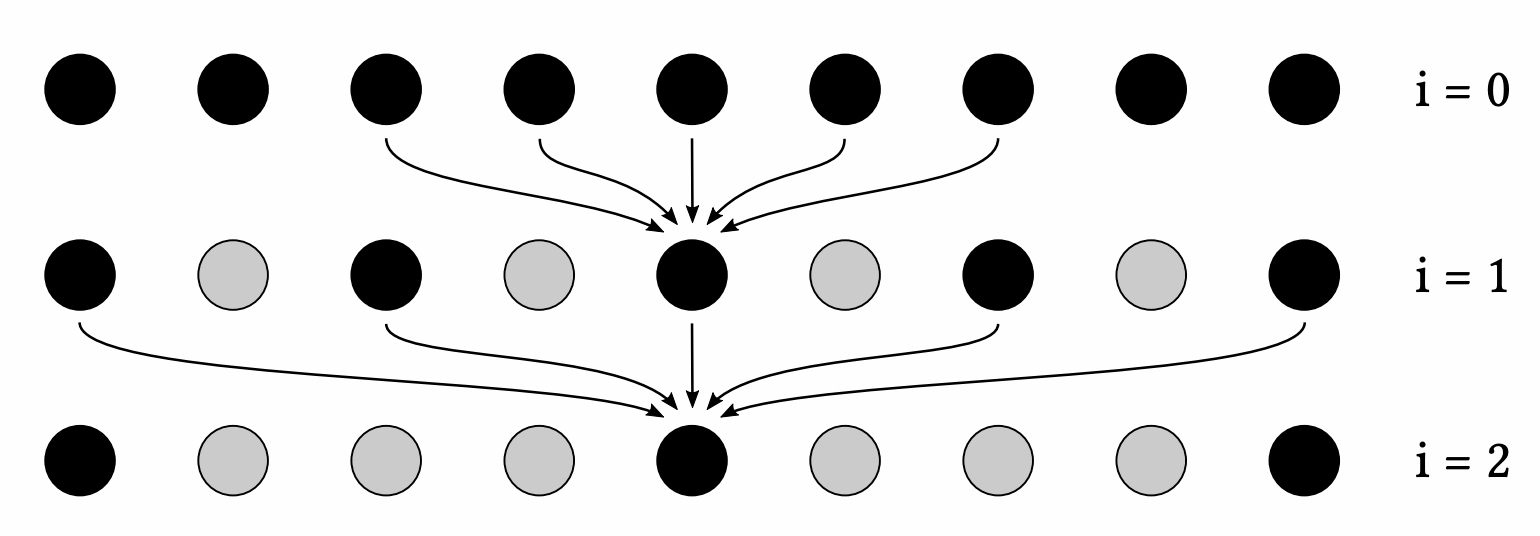
  上图展示了一维情况下的多次滤波过程。每次采样的点固定为$5$个，但采样点的间隔会随着迭代次数的增加而增大（上图中黑色的点就是采样点）。通过这种方式来近似实现$64\times 64$滤波器，而实际的开销仅为$5^2\times 5$，这是一个非常明显的采样开销优化。

  关于空间域滤波就简单总结到这里，而空间域滤波SOTA方法SVGF（Spatiotemporal Variance-Guided Filter）以后涉及到了再详细总结一下。

四、Outlier噪点去除

  大部分情况下，降噪滤波的效果非常明显，图像变得非常干净。但有时滤波之后图像依旧存在一些噪声点，这些噪声点表现为强烈明亮的白色，如下图5所示。这是因为这些噪点的取值已经远远超过像素常见的取值，滤波降噪的加权平均在绝对大的取值面前也显得无能为力。这种噪声点被称为Outlier。

图5 滤波后图像依旧存在Outlier噪点

  Outlier噪点不能通过滤波器去掉，必须要通过一些手段识别出这些噪点，然后再针对性地去除。识别检测的算法很简单，其核心的思路可以总结为：对于每个像素$(x,y)$，对以该像素$(x,y)$为中心的邻域（例如$7\times 7$大小的邻域范围）统计像素的均值$\mu$和方差$\sigma$，像素取值$I(x,y)$超出$[\mu-k\sigma,\mu+k\sigma]$范围的就是Outlier噪点！其中$k$是可调整的参数，可以通过该参数来调整区间范围。

  对于超过$[\mu-k\sigma,\mu+k\sigma]$范围的像素，直接令像素值Clamp到$[\mu-k\sigma,\mu+k\sigma]$范围内即可（例如大于$\mu+k\sigma$，那么令像素取值为$\mu+k\sigma$）。这种Clamp方法在也被应用到时间域降噪算法中解决拖影问题。在时间域滤波中，滤波公式为：

$$\overline C^{(i)}=\alpha \overline C^{(i)}+(1-\alpha)C^{(i-1)}$$

  拖影现象产生的根源来自于$C^{(i-1)}$与$C^{(i)}$并非是同一个着色点，因此Clamp方法就是对$C^{(i-1)}$做限制：

$$\mathbf{clamp}(C^{(i-1)},\mu-k\sigma,\mu+k\sigma)$$

  其中$\mu$和$\sigma$是当前帧$C^{(i)}$邻域范围内的像素均值和方差。这种方法使得$C^{(i-1)}$和$C^{(i)}$不至于差距过大，一定程度上解决了时间域滤波的拖影问题。

Reference

$[1]$ Johannes Kopf, Michael F. Cohen, Dani Lischinski, and Matt Uyttendaele. 2007. Joint bilateral upsampling. ACM Trans. Graph. 26, 3 (July 2007), 96–es.

$[2]$ GAMES202: 高质量实时渲染