高质量实时渲染：基于物理的BRDF材质

本文是闫令琪老师GAMES202高质量实时渲染课程的学习笔记和总结，这一节的主题为基于物理的BRDF材质模型，涉及的内容有基于微表面理论的BRDF材质模型、迪士尼原则的BRDF材质模型、Kulla-Conty近似以及基于LTC的实时面光源光照着色算法。

  在实时渲染领域，所谓的基于物理的材质模型实际上也并非真正的物理准确，只是相对于传统的基于经验的材质模型更具物理特性，渲染的效果更为真实一些。这里提到的材质模型均为物体表面材质模型，对于介质散射的材质模型这里不作介绍。当前基于物理的表面材质模型可以分为两大类，分别是基于微表面的材质模型和迪士尼原则的材质模型。其中迪士尼原则的材质模型对艺术家根据参数调整材质效果更为友好，因而得到了广泛的应用。

一、基于微表面的BRDF模型

  基于微表面的BRDF模型本质上通过宏观的概率分布来描述微观层面下的微平面朝向等属性。基于微表面的BRDF模型将物体表面建模为许多个不同朝向的微平面（Microfacet）组成，正如下图1所示：

图1 微表面模型

  基于微表面的Cook-Torrance BRDF模型核心公式如下：

$$f(\omega_i, \omega_o)=\frac{\mathbf{F}(\omega_i,h)\mathbf{G}(\omega_i,\omega_o,h)\mathbf{D}(h)}{4(n\cdot \omega_i)(n\cdot \omega_o)} \tag {1}$$

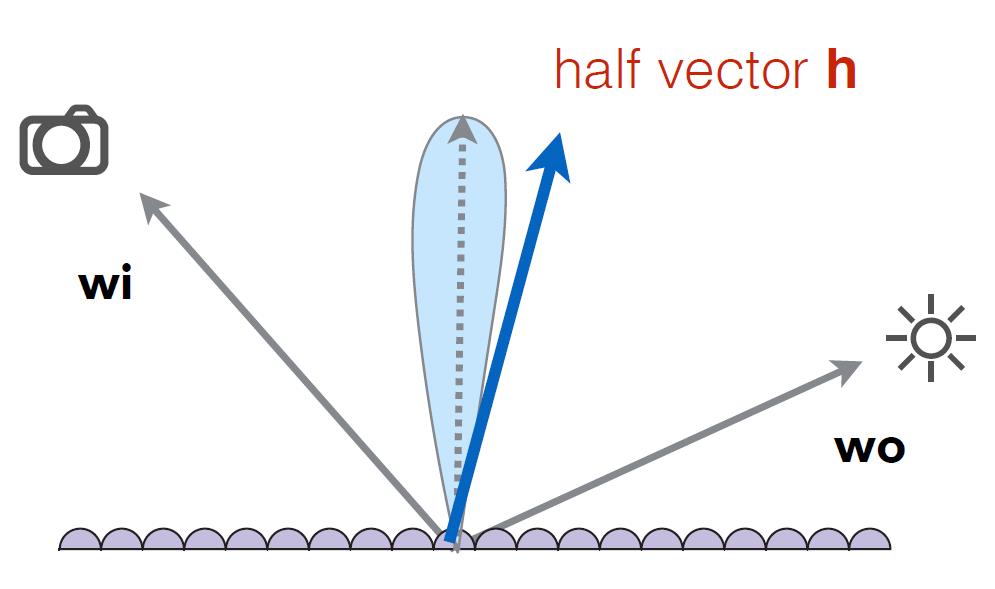
  其中$\omega_i$、$\omega_o$和$n$分别是观察方向、入射方向以及法线方向，而$h$是介于$\omega_i$和$\omega_o$之间的半角向量（half vector），这些均是归一化之后的单位向量（如下图2所示）。而公式中的$\mathbf{F}(\omega_i,h)$、$\mathbf{G}(\omega_i,\omega_o,h)$和$\mathbf{D}(h)$分别是菲涅尔反射方程、几何函数和法线分布函数。菲涅尔方程描述的是在不同的观察角度下表面反射的光线比率，几何函数描述微平面自我遮挡的属性，而法线分布函数估算在给定粗糙程度下的微平面朝向与半角向量一致的数量。

图2 BRDF输入参数

  下面分别对$\mathbf{F}(\omega_i,h)$、$\mathbf{G}(\omega_i,\omega_o,h)$和$\mathbf{D}(h)$做一个总结。

1、菲涅尔反射方程

  菲涅尔反射方程计算给定观察角度下的反射率（reflectance）。如下图3所示，从左到右，观察视角$\omega_i$与桌面法线的夹角越来越大（特别是Grazing angle，即夹角接近于$90$度，姑且称之为“擦边视角”吧），桌面上反射的内容越来越多，即反射率越来越大。若视角垂直地观察桌面（即观察视角$\omega_i$与法线同向平行了），则可以观察到桌面反射的内容最少，此时只有一个最基础的反射率。

图3 不同观察角度下的桌面反射程度

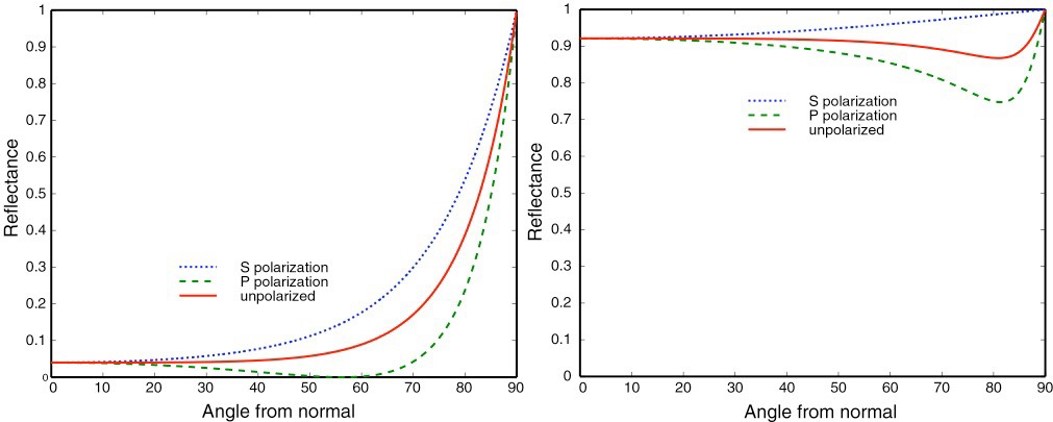
  对于绝缘体（Dielectric），其菲涅尔反射率变化符合本文上面提到的情况（即夹角越大，反射率越高）。而对于导体（Conductor），其菲涅尔反射率基本不会发生太大的变化，均保持一个比较高的反射率。下图4分别给出了绝缘体（图左）和导体（图右）随着与法线夹角增大时的反射率变化曲线。

图4 绝缘体（左）、导体（右）反射率随与法线夹角增大的变化曲线

  物理准确的菲涅尔项需要考虑光线极化（polarization），其公式比较复杂：

$$\begin{align} R_s=&|\frac{\eta_1 cos\theta_i-\eta_2cos\theta_t}{\eta_1cos\theta_i+\eta_2cos\theta_t}|^2 =|\frac{\eta_1 cos\theta_i-\eta_2\sqrt{1-(\frac{\eta_1}{\eta_2}sin\theta_i)^2}}{\eta_1cos\theta_i+\eta_2\sqrt{1-(\frac{\eta_1}{\eta_2}sin\theta_i)^2}}|^2\\ R_p=&|\frac{\eta_1 cos\theta_t-\eta_2cos\theta_i}{\eta_1cos\theta_t+\eta_2cos\theta_i}|^2 =|\frac{\eta_1 \sqrt{1-(\frac{\eta_1}{\eta_2}sin\theta_i)^2}-\eta_2cos\theta_i}{\eta_1\sqrt{1-(\frac{\eta_1}{\eta_2}sin\theta_i)^2}+\eta_2cos\theta_i}|^2\\ R_{eff}=&\frac12(R_s+R_p) \end{align} \tag {2}$$

  其中$\eta_1$和$\eta_2$分别是入射介质（例如空气）和折射介质的折射系数，$\theta_i$和$\theta_t$是入射角和折射角。在实时渲染领域，一种常见的、更为简单的菲涅尔项近似公式如下所示（注：这里的$\omega_i$是观察方向）：

$$\mathbf{F}(\omega_i,h)=\mathbf{R}_0+(1-\mathbf{R}_0)(1-(\omega_i\cdot h))^5 \tag {3}$$

  上述公式中的$\mathbf{R}_0$是基础反射率，它通过入射介质和折射介质的折射系数计算给出：

$$\mathbf{R}_0=(\frac{\eta_1-\eta_2}{\eta_1+\eta_2})^2 \tag {4}$$

  公式$(3)$本质上就是对基础反射率做一个非线性插值。关于BRDF的菲涅尔项就总结到这里。

2、法线分布函数

  法线分布函数$\mathbf{D}(h)$（简称NDF）可以看成一个概率分布函数：输入半角向量$h$，它返回$[0,1]$的概率值，表示该表面的所有微平面中，有多少比例的微平面法线朝向$h$。故此，若微平面朝向越一致、越集中，则物体表面材质越倾向于glossy甚至是specular；反之微平面朝向越分散、越混乱，则物体表面材质越倾向于diffuse。在此，基于微表面的BRDF采用粗糙度（roughness）系数来衡量表面的粗糙程度，它的取值为$[0,1]$，在此我们记为$\alpha$。

  Beckmann的NDF是一个比较有名的法线分布函数，其公式为：

$$\mathbf{D}(h)=\frac{e^{\frac{(n\cdot h)^2-1}{\alpha^2(n\cdot h)^2}}}{\pi\alpha^2(n\cdot h)^4} \tag {5}$$

  其中$n$是表面的宏观法线。事实上，在各种实时渲染引擎中，现在更为常用和流行的NDF是GGX（Trowbridge-Reitz）法线分布函数。其公式为：

$$\mathbf{D}(h)=\frac{\alpha^2}{\pi((n\cdot h)^2(\alpha^2-1)+1)^2} \tag {6}$$

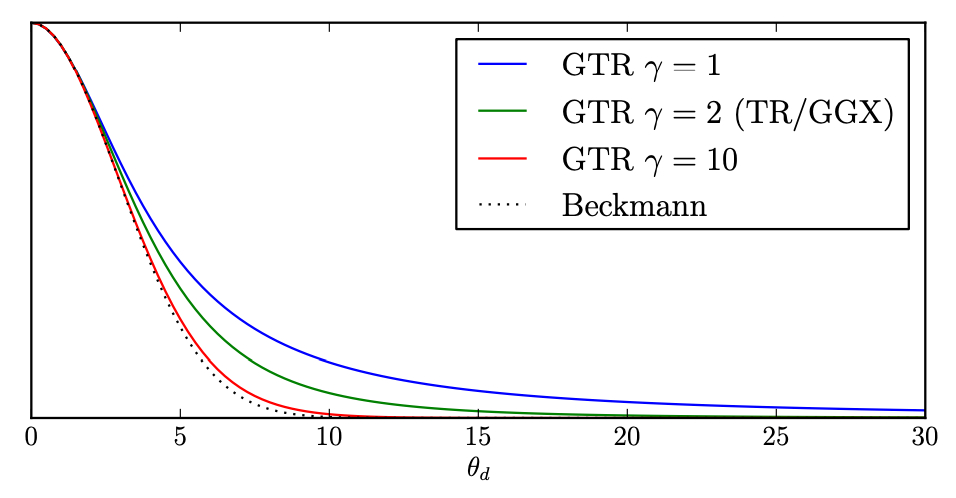
  相较于Beckmann等其他分布函数，GGX分布的特点就是具有最长的高光尾部（long tail），如下图5所示。这个特点表现为高光边缘的光晕效果，看起来更为炫酷和真实。这种效果本质上是因为GGX分布在高光边缘部分衰减得比较慢。

图5 Beckmann分布和GGX分布的光照结果比较

  图6给出了GGX分布和Beckmann分布函数曲线图，这两种分布函数形状均与高斯分布类似，该图的横坐标为宏观法线$n$和半角向量$h$的夹角。Beckmann分布在接近$\pi /2$（或者$-\pi/2$）时剧烈衰减到零，而GGX分布变化较缓，而且在$\pi/2$时始终保持一定的值。这就解释了GGX的长高光尾部的原因。

图6 Beckmann分布和GGX分布曲线图

  继GGX之后，Brent Burley将其扩展到了一个更为通用的NDF模型——GTR分布（Generalized Trowbridge-Reitz，简称GTR）。GTR分布允许通过参数来主动调整高光的尾部长度，其未归一化的计算公式为：

$$\mathbf{D}(h)=\frac{1}{(1+(n\cdot h)^2(\alpha^2-1))^{\gamma}} \tag {7}$$

  GTR分布的归一化因子计算公式为：

$$k(\alpha,\gamma)=\frac{(\gamma -1)(\alpha^2-1)}{\pi (1-\alpha^{2(1-\gamma)})} \tag {8}$$

  该归一化因子函数在$\alpha=1$或者$\gamma=1$时有奇异点，但根据极限逼近原理可将这些奇异点去除$^{[1]}$：

$$\begin{align} k(\alpha,1.0)=&\frac{(\alpha^2-1)}{\pi \mathbf{ln}(\alpha^2)}\\ k(1.0,\gamma)=&\frac{1}{\pi} \end{align}$$

  因此实际使用的归一化GTR分布计算公式$^{[1]}$为：

$$\mathbf{D}(h)=\frac{k(\alpha,\gamma)}{(1+(n\cdot h)^2(\alpha^2-1))^{\gamma}} \tag {10}$$

  GTR分布公式中的$\gamma$用于控制NDF的形状（特别是高光尾部）。如下图7所示，当$\gamma=2$时，GTR分布就是GGX分布；而当$\gamma=10$时，GTR分布非常接近于Beckmann分布。

图7 GTR分布

3、几何函数

  几何函数项$\mathbf{G}(\omega_i,\omega_o,h)$考虑微平面之间的相互遮挡现象。如下图8所示，光线打到某个微平面之前可能被其他的微平面遮挡，从而产生Shadowing现象（图左）；同样地，微平面反射光线到视角之前亦可能被其他的平面遮挡，从而产生Masking现象（图右）。因此几何函数项又被称为Shadowing-Masking项。这两种现象在”擦边视角”（即前面提到的Grazing Angle）下更容易产生。

图8 Shadowing现象（左）和Masking现象（右）

  因此，Shadowing和Masking现象会导致光照的结果变暗，特别是在”擦边视角”下。一种常用的几何函数是GGX分布与Schlick-Beckmann近似的结合体，其计算公式为：

$$\mathbf{G_{SchlickGGX}}(n,v)=\frac{n\cdot v}{(n\cdot v)(1-\kappa)+\kappa} \tag {11}$$

  其中，$n$是给定的法线向量，$v$指定的观察方向（可以是观察视角$\omega_i$，也可以是光线视角$\omega_o$）。$\kappa$是粗糙度重映射因子，根据是直接光照还是IBL光照进行调整：

$$\begin{align} \kappa_{direct}=&\frac{(\alpha+1)^2}{8}\\ \kappa_{IBL}=&\frac{\alpha^2}{2} \end{align}$$

  为了综合考虑Shadowing现象和Masking现象，因此Smith几何函数项采用公式$(11)$合并而成：

$$\mathbf{G}(\omega_i,\omega_o,h)=\mathbf{G_{SchlickGGX}}(h,\omega_i)\cdot \mathbf{G_{SchlickGGX}}(h,\omega_o) \tag {12}$$

  下图9展示了不同粗糙度下的几何遮蔽效果。几何函数的值域亦为$[0,1]$。当物体表面较为粗糙时，在”擦边视角”光照边缘部分，会有一个明显的光照衰减效果，这就是Shadowing-Masking项的作用。

图9 不同粗糙度下的几何函数遮蔽效果

二、迪士尼原则的BRDF模型

  前面提到的Cook-Torrance BRDF模型对不了解其中基础原理的艺术家们并不友好（例如复数的折射系数），而且该BRDF模型不能表示一些日常生活常见的材质（例如一个diffuse物体表面刷上一层清漆）。针对这些问题，迪士尼原则的BRDF模型应运而生。迪士尼原则有如下几点：

• 材质的可调整参数要求尽可能地直观，而非直接使用具备物理涵义的参数；
• 材质可调整的参数应该尽可能地少；
• 将材质可调整的参数在合理的取值范围内重新调整映射为$[0,1]$的值域；
• 当艺术们认为有意义时，材质可调整的参数允许被设置为超出正常范围之外的取值；
• 所有可调整的材质参数组合起来的效果应该尽可能地鲁棒和合理。

  迪士尼原则的BRDF模型总的来说可以分成三层，分别是漫反射层、镜面高光层和表面清漆层。诸如车漆、木质地板等材料可以通过一个两层模型来渲染：上面是一层透明材料，通常比较光滑，下面则是漫反射或金属等其他材料。如果要仔细地渲染这一模型，我们需要考虑两层间的多次反射和折射，并用fresnel公式来分配每次反射/折射的比例。Disney BRDF采用的方案要简单粗暴得多——加上一个额外的高光，称为清漆（clearcoat）项。

  迪士尼原则的BRDF核心计算公式如下所示，比较复杂：

$$f(\omega_i,\omega_o)=(1-\sigma_m)(\frac{C}{\pi}\mathbf{mix}(f_d(\omega_i,\omega_o),f_{ss}(\omega_i,\omega_o),\sigma_{ss})+f_{sh}(\omega_i,\omega_o))+\\\frac{\mathbf{F}_s(\theta_d)\mathbf{G}_s(\omega_i,\omega_o)\mathbf{D}_s(h)}{4(n\cdot \omega_i)(n\cdot \omega_o)}+\frac{\sigma_c}{4}\frac{\mathbf{F}_c(\theta_d)\mathbf{G}_c(\omega_i,\omega_o)\mathbf{D}_c(h)}{4(n\cdot\omega_i)(n\cdot \omega_o)} \tag {13}$$

  其中$\theta_d$是$\omega_i$和$\omega_o$之间的夹角，$C$是物体物体表面的基础颜色值。记$\theta_i$和$\theta_o$分别为$\omega_i$和$\omega_o$与法线$n$的夹角。$f_d(\omega_i,\omega_o)$是漫反射项：

$$\begin{align} f_d(\omega_i,\omega_o)=&(1+(F_{D90}-1)(1-cos\theta_i)^5)(1+(F_{D90}-1)(1-cos\theta_o)^5)\\ F_{D90}=&0.5+2\sigma_rcos^2\theta_d \end{align} \tag {14}$$

  公式$(13)$中的$f_{ss}(\omega_i,\omega_o)$是次表面散射项：

$$\begin{align} f_{ss}(\omega_i,\omega_o)=&1.25(F_{ss}(1/(cos\theta_i+cos\theta_o)-0.5)+0.5)\\ F_{ss}=&(1+(F_{ss90}-1)(1-cos\theta_i)^5)(1+(F_{ss90}-1)(1-cos\theta_o)^5)\\ F_{ss90}=&\sigma_rcos^2\theta_d \end{align} \tag {15}$$

  公式$(13)$中的$f_{sh}(\omega_i,\omega_o)$是漫反射sheen项：

$$\begin{align} f_{sh}(\omega_i,\omega_o)=&\mathbf{mix}(1,C_{tint},\sigma_{sht})\sigma_{sh}(1-cos\theta_d)^5\\ C_{tint}=&\frac{C}{\mathbf{lum}(C)} \end{align} \tag {16}$$

  其中$\mathbf{lum}$函数是求相对亮度的函数，对线性RGB颜色空间的表面基础颜色$C$有：

$$\mathbf{lum}(C)\approx 0.2126\cdot C_r+0.7152\cdot C_g+0.0722\cdot C_b$$

  公式$(13)$中的$\mathbf{F}_s(\theta_d)$是镜面高光菲涅尔项，同样是用Schlick公式近似计算，但Schlick公式中的基础反射率$\mathbf{R}_0$是利用金属度参数进行混合插值：

$$\begin{align} \mathbf{F}_s(\theta_d)=&C_s+(1-C_s)(1-cos\theta_d)^5\\ C_s=&\mathbf{mix}(0.08\sigma_s\cdot \mathbf{mix}(\mathbf{1},C_{tint},\sigma_{st}),C,\sigma_m) \end{align} \tag {17}$$

  公式$(13)$中的$\mathbf{G}_s(\omega_i,\omega_o)$镜面高光的几何函数项，这里采用各项异性GGX函数（$\alpha_x$和$\alpha_y$计算见公式$(19)$）：

$$\begin{align} \mathbf{G}_s(\omega_i,\omega_o)=&G_{s1}(\omega_i)\cdot G_{s1}(\omega_o)\\ G_{s1}(\omega)=&\frac{1}{1+\Lambda_s(\omega)}\\ \Lambda_s(\omega)=&\frac12+\frac12\sqrt{1+(\alpha^2_xcos^2\phi+\alpha^2_ysin^2\phi)tan^2\theta} \end{align} \tag {18}$$

  公式$(13)$中的$\mathbf{D}_s(h)$是镜面高光的法线分布函数，采用$\gamma=2$的GTR分布函数：

$$\begin{align} \mathbf{D}_s(h)=&\frac{1}{\pi \alpha_x\alpha_y(sin^2\theta_h\cdot (\frac{cos^2\phi_h}{\alpha^2_x}+\frac{sin^2\phi_h}{\alpha^2_y})+cos^2\theta_h)^2}\\ \alpha_x=&\sigma^2_r/a,\ \alpha_y=\sigma^2_r\cdot a\\ a=&\sqrt{1-0.9\sigma_a} \end{align} \tag {19}$$

  公式$(13)$中的$\mathbf{F}_c(\theta_d)$是表面清漆层的菲涅尔项，采用折射率固定为$1.5$的绝缘体Schlick近似公式：

$$\mathbf{F}_c(\theta_d)=0.04+0.96(1-cos\theta_d)^5 \tag {20}$$

  公式$(13)$中的$\mathbf{G}_c(\omega_i,\omega_o)$是表面清漆层的几何函数项，采用粗糙度（即下式的$\alpha$）为$0.25$的各向同性GGX分布函数：

$$\begin{align} \mathbf{G}_c(\omega_i,\omega_o)=&G_{c1}(\omega_i)\cdot G_{c1}(\omega_o)\\ G_{c1}(\omega)=&\frac{1}{1+\Lambda_c(\omega)}\\ \Lambda_c(\omega)=&-\frac12+\frac12\sqrt{1+\alpha^2tan^2\theta} \end{align} \tag {21}$$

  最后公式$(13)$中的$\mathbf{D}_c(h)$是表面清漆层的法线分布函数，采用各向同性的$\gamma=1$的GTR分布：

$$\begin{align} \mathbf{D}_c(h)=&\frac{\alpha^2-1}{2\pi \mathbf{ln}\alpha(\alpha^2cos^2\theta_h+sin^2\theta_h)}\\ \alpha=&\mathbf{mix}(0.1,0.01,\sigma_{cg}) \end{align} \tag {22}$$

  以上就是Disney BRDF的全部公式，综合考虑的因素比较多，因此公式也比较复杂繁琐。上面公式频繁提及的$\mathbf{mix}$函数就是一个线性混合函数，即$\mathbf{mix}(x,y,a)=x(1-a)+ya$。Disney BRDF总的可调整参数有10个，如下图10所示，因此具备较大的灵活调整空间。

• 次表面散射（subsurface）参数$\sigma_{ss}$：模拟漫反射的次表面散射现象，次表面散射的材质呈现更为平坦的效果（即原本漫反射的立体感被削弱了）；
• 金属度（metallic）参数$\sigma_m$：度量材质的金属特性，$\sigma_m=0$就是绝缘体，$\sigma_m=1$就是纯粹的金属导体；
• 高光度（specular）参数$\sigma_s$：控制镜面高光的反射强度，类似于Blinn-Phong模型的$k_s$参数；
• 高光反射颜色(specularTint）参数$\sigma_{st}$：控制镜面反射的颜色，$\sigma_{st}=0$时为纯白光反射，$\sigma_{st}=1$时为指定的材质颜色反射；
• 粗糙度（roughness）参数$\sigma_r$：控制材质表面的粗糙度，与在Cook-Torrance BRDF的参数含义相同；
• 各向异性度（anisotropic）参数$\sigma_{a}$：反映材质的各向异性程度，用于控制镜面反射高光的纵横比，$\sigma_a=0$代表完全各向同性，反之$\sigma_a=1$代表完全各向异性；
• 光泽度（sheen）参数$\sigma_{sh}$：控制额外的掠射分量（grazing component）的效果，主要用于布料，正如下图所示，它会在“擦边视角”区域产生一种泛白的效果（有点像布料的表面绒毛）；
• 光泽颜色（sheenTint）参数$\sigma_{sht}$：控制sheen效果的颜色，$\sigma_{sht}=0$时为完全白色的绒毛效果，$\sigma_{sht}=1$时为绒毛的颜色是指定的材质颜色；
• 清漆强度（clearcoat）参数$\sigma_{c}$：控制表面上层清漆材质的效果，$\sigma_c=0$时为完全无清漆效果，$\sigma_c=1$时为清漆效果最大化；
• 清漆光泽度（clearcoatGloss）参数$\sigma_{cg}$：控制表面上层清漆材质的光滑程度。

图10 Disney BRDF可调整参数列表

  这里给出了官方实现的Shader代码，可以结合代码做进一步的理解。

三、Kulla-Conty材质多次弹射近似

  这里回到基于微平面理论的Cook-Torrance BRDF模型。基于微平面的BRDF存在这么一个问题：如下图11所示，随着表面粗糙度的增大，物体表面反射的总能量越来越少，这导致渲染出来的物体表面越来越暗，这种现象根源于Cook-Torrance BRDF能量不守恒的致命缺陷。

图11 从左到右，粗糙度逐渐增大，物体反射的能量越来越少（暗）

  这种能量不守恒的背后原因并不难理解，当表面的粗糙度增大时，微平面的朝向排列更为混乱，导致某个微平面的反射光线大概率会被其他微平面遮挡住，因而总的反射能量会缺失这些被遮挡的光线的能量贡献，最终使得入射光的能量（减去物体表面吸收的能量）与表面反射的能量不对等。理论上，这些被遮挡的光线会经过多次弹射然后再反射出来，但Cook-Torrance BRDF并没有考虑这类复杂的多次弹射现象，该BRDF本质上只计算一次弹射贡献的能量。所以，对于光滑的表面，Cook-Torrance BRDF几乎可以实现能量守恒，但对于粗糙的表面则存在明显的能量不守恒现象。

  为了弥补那些被丢失的能量，实时渲染领域的一种方法就是Kulla-Conty近似。首先，Kulla-Conty先计算单次弹射的能量占比（也就是Cook-Torrance BRDF计算出来的能量比例，这个比例是$[0,1]$的某个值）。结合BRDF的定义（反射的辐射率Radiance除以接收的辐照度Irradiance），在给定的出射方向$\mu_0$上，BRDF反射的能量比例为：

$$E(\mu_o)=\int_{0}^{2\pi}\int_{0}^1f(\mu_o,\mu_i,\phi)\mu_i d\mu_i d\phi \tag {23}$$

  其中$\mu_i=sin\theta_i$。上述的公式就是半球方向上的入射角度进行BRDF的积分，从而得出反射到$\mu_o$的总的能量占比。由此，剩余发生弹射多次的能量占比就为（先不考虑物体吸收现象，即假设物体颜色为纯白色）：

$$1-E(\mu_o) \tag {24}$$

  Kulla-Conty近似的核心思路就是想办法把剩余能量$1-E(\mu_o)$以某种公式弥补到初始的BRDF中，从而近似实现能量守恒。因此，Kulla-Conty近似在原本Cook-Torrance BRDF的基础上设计新增了一个新的BRDF函数：

$$\begin{align} f_{ms}(\mu_o,\mu_i)=&\frac{(1-E(\mu_o))(1-E(\mu_i))}{\pi(1-E_{avg})}\\ E_{avg}=&2\int_0^1 E(\mu)\mu d\mu \end{align} \tag {25}$$

  这里不把具体的推导过程放上来。这个BRDF计算涉及到$E(\mu)$和$E_{avg}$的积分公式，可以通过预计算打表来实现快速的计算:

• 对于$E(\mu)$：依赖的参数有粗糙度和$\mu$，因此可以预计算一个二维的表；
• 对于$E_{avg}$：依赖的参数仅有粗糙度，因此可以预计算一个一维的表。

  把公式$(25)$的BRDF加到原本的Cook-Torrance BRDF上，从而弥补了先前缺失的反射能量。下图给出了处理前后的效果比较，当粗糙度比较大时，表面反射的亮度有明显的差距，这才是能量守恒时的渲染结果。

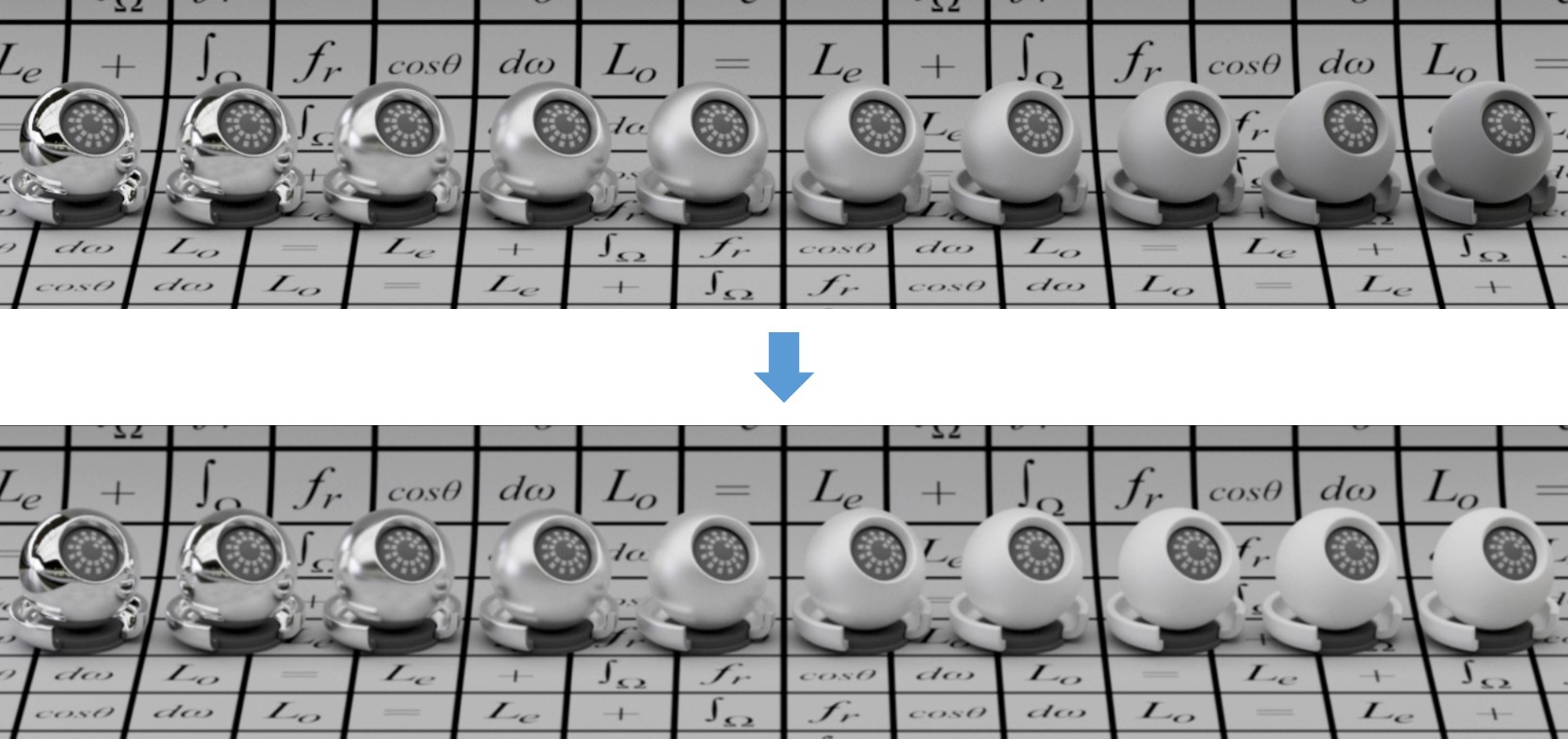
  上面我们不考虑物体吸收能量的现象，即假设了物体表面的颜色均为纯白色。为了支持设定任意的材质Albedo，前面的公式$(25)$需要进一步考虑物体材质的反照率。首先定义一个平均菲涅尔反射率来度量多少能量被反射了：

$$F_{avg}=\frac{\int_0^1 F(\mu)\mu d\mu}{\int_o^1 \mu d\mu}=2\int_0^1 F(\mu)\mu d\mu \tag {26}$$

  菲涅尔项$F(\mu)$的基础反射率$R_0$是RGB向量，因此上面的$F_{avg}$也是一个RGB向量。仔细观察公式$(25)$中$E_{avg}$的计算公式，不难理解$E_{avg}$衡量了单次弹射之后向半球所有方向反射（不会参与后续的多次弹射）的能量比例。因此有如下推理：

• 能够直接观察到的反射能量比例为：$F_{avg}\cdot E_{avg}$（即反射能量乘以反射率）；
• 经过一次弹射之后反射的能量比例：$F_{avg}\cdot (1-E_{avg})\cdot F_{avg}\cdot E_{avg}$；
• ……
• 经过$k$次弹射之后反射的能量比例：$F^k_{avg}\cdot (1-E_{avg})^k\cdot F_{avg}\cdot E_{avg}$；

  把$k=0$到$k\to \infty$的所有能量加起来，可以得到一个级数求和公式，它考虑了物体吸收之后剩余的所有反射的能量比例，该级数最终收敛值为：

$$\frac{F_{avg}\cdot E_{avg}}{1-F_{avg}(1-E_{avg})} \tag {27}$$

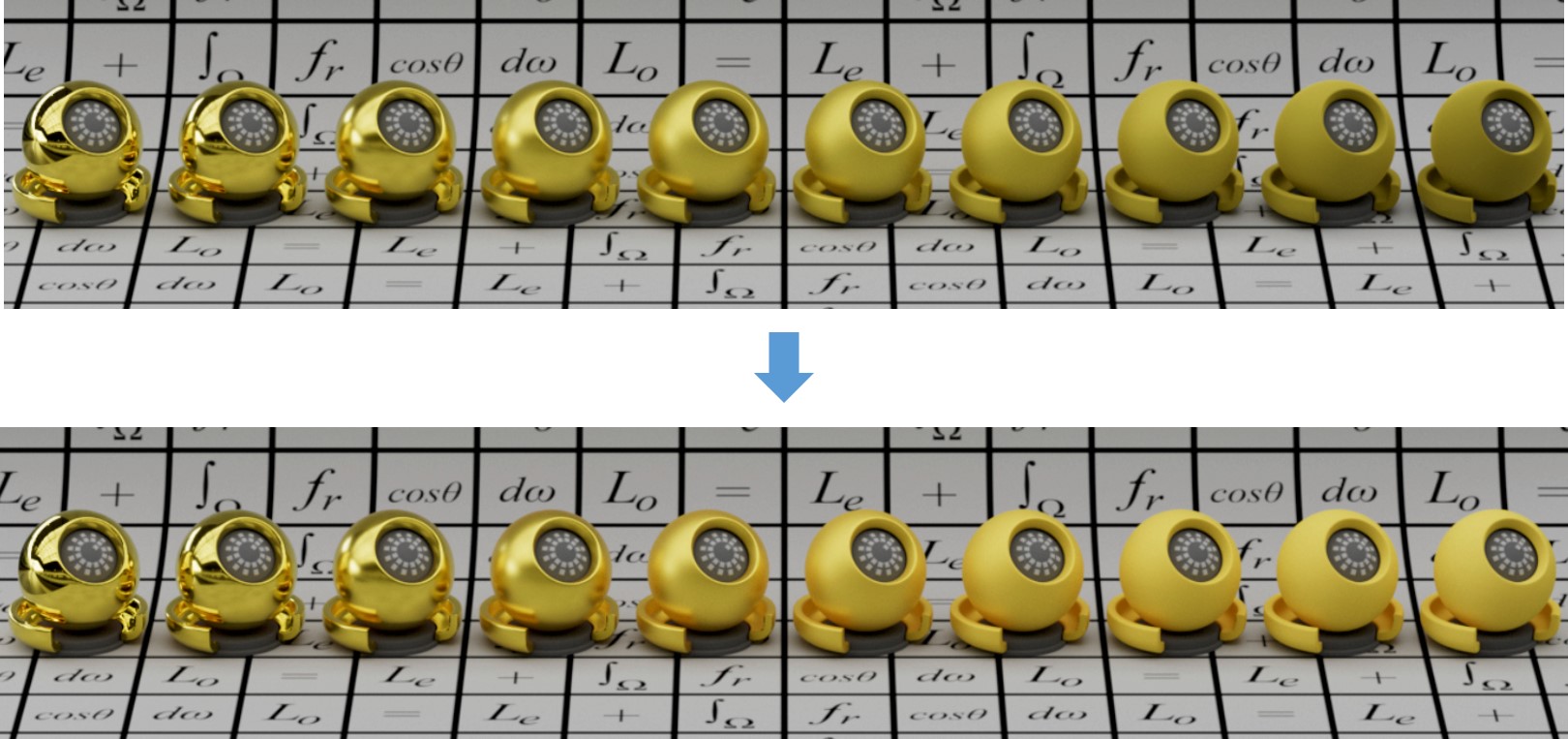
  公式$(27)$就是Kulla Conty的颜色项，最终增加的BRDF计算公式为：

$$f_{ms}(\mu_o,\mu_i)=\frac{F_{avg}\cdot E_{avg}}{1-F_{avg}(1-E_{avg})}\cdot\frac{(1-E(\mu_o))(1-E(\mu_i))}{\pi(1-E_{avg})} \tag {28}$$

  因此，为了考虑物体的能量吸收现象，需要再预计算平均菲涅尔反射$F_{avg}$。下图给出了考虑材质颜色的处理前后结果对比。

四、基于LTC的实时面光源光照

  在真实世界中，面光源是更为常见的光源类型。对于图形渲染来说，实现面光源的着色光照能够极大地增强渲染真实感。然后求解面光源的着色光照理论上需要计算球面上的积分方程，这对于实时渲染来说是一个棘手的难题。由此，论文$^{[2]}$提出了一种基于LTC（Linearly Transformed Cosines）的实时面光源光照算法。

图12 面光源的光照着色积分

  如上图12所示，面光源的着色需要在光源覆盖的球面区域上对BRDF和入射辐射率进行积分计算。因此，对于实时渲染来说，面光源的光照着色主要有以下两个挑战：

• 这是一个球面上的球面分布函数积分，积分的区域随着面光源的不同而变化；
• 基于物理的表面材质是一个比较复杂的函数，很难用简单的分布函数来描述它。

1、球面分布线性变换

  为了将基于物理的材质函数转换成某种简单的分布函数，以便后续的光照积分计算，作者首先提出了球面分布线性变换（Linearly Transformed Spherical Distributions，简称LTSDs）的概念。所谓的球面分布线性变换，其实就是将一个原始的球面分布函数（因此其输入的参数为球面方向，例如$\omega_o$），通过应用某种线性变换的操作将其变换到另一个球面分布函数。

  记$D_o$为原始的球面分布函数，其输入参数为$\omega_o$，$D$为变换后的球面分布函数，变换后的方向参数为$\omega$，变换矩阵为$3\times 3$大小的$M$。虽然这里说的是对球面分布函数进行矩阵$M$的线性变换，但实际上是对输入的方向参数$\omega_o$进行线性变换，因此有如下的关系：

$$\begin{align} \omega=&\frac{M\omega_o}{||M\omega_o||}\\ \omega_o=&\frac{M^{-1}\omega}{||M^{-1}\omega||} \end{align} \tag {29}$$

  $\omega$和$\omega_o$都是单位向量，因此做了归一化。由此，变换后的分布$D$就是原分布$D_o$再乘上$\omega_o$变换到$\omega$的Jacobian：

$$D(\omega)=D_o(\omega_o)\frac{\partial \omega_o}{\partial \omega}=D_o(\frac{M^{-1}\omega}{||M^{-1}\omega||})\frac{|M^{-1}|}{||M^{-1}\omega||^3} \tag {30}$$

  对于方向向量来说，如果$M$是缩放矩阵，那么$M$不会改变$\omega_o$向量的方向，即$\partial \omega_o/\partial\omega=1$，这意味着矩阵$M$的缩放分量不会改变原始的$D_o$分布大小，即该变换具有形状不变性（Shape Invariance）。除此之外，LTSDs变换还具备以下的关键性质：

$$\int_{\Omega}D(\omega)d\omega=\int_{\Omega}D_o(\omega)\frac{\partial \omega_o}{\partial \omega}d\omega=\int_{\Omega}D_o(\omega_o)d\omega_o \tag {31}$$

  即原始分布$D_o$对于球面上的$\omega_o$积分等价于变换后的分布$D$对$\omega$的球面积分。

2、用LTC近似基于物理的BRDF材质

  论文$^{[2]}$中使用的原始球面分布函数$D_o$是clamped cosine分布，即：

$$D_o(\omega_o=(x,y,z))=\frac{1}{\pi}\mathbf{max}(0,z) \tag {32}$$

  而对于基于微平面模型的BRDF材质，作者希望用上述的clamped cosine分布来近似BRDF分布（注：这里的BRDF暂时不考虑菲涅尔项，即菲涅尔项恒为$1$），因此记：

$$D\approx \rho(\omega_v,\omega_l)cos\theta_l \tag {33}$$

  其中$\omega_l$是光照方向，$\omega_v$是观察方向，$\theta_l$是$\omega_l$与法线的夹角。对于各向同性的BRDF，在确定了观察方向$\omega_v=(sin\theta_v,0,cos\theta_v)$和粗糙度系数$\alpha$之后，公式$(33)$的$D$就只依赖于$\omega_l$，因此可以把它看成是一个球面分布函数。对于任意的$(\theta_v,\alpha)$组合，我们寻找一个变换矩阵$M$，使得公式$(32)$的$D_o$分布能够通过该矩阵$M$变换到公式$(33)$的$D$分布。论文$^{[2]}$指出，矩阵$M$应该是如下的形式：

$$M= \left[ \begin{matrix} a & 0 & b\\ 0 & c & 0\\ d & 0 & 1 \end{matrix} \right] \tag {34}$$

  矩阵$M$中有四个参数需要确定，这些参数的计算是通过预先离线计算好并存储到纹理中，在渲染时直接查找获取。当然实际需要的是$M^{-1}$，因此存储的时候$M^{-1}$的四个参数。存储参数的纹理是一个二维纹理，将$\theta_v$和$\alpha$离散化成纹理的$u$和$v$轴。在实际的实现中，纹理的$u$坐标对应$\theta_v$离散化$[0,\frac{\pi}{2}]$的取值，$v$坐标对应$\sqrt \alpha$离散化$[0,1]$的取值。除了上面提到的四个参数之外，我们还会预计算$D$分布的范数：

$$\int_{\Omega}\rho(\omega_v,\omega_l)cos\theta_ld\omega_l$$

  这个范数后面会用到，所以一共五个参数。矩阵$M$四个参数的拟合计算本质上使用了凸优化的策略，这里不再详细展开。

3、基于LTC的面光源着色

  对于diffuse的面光源光照着色，我们需要求解以下的积分公式：

$$I=\int_{P}L(\omega_l)\rho(\omega_v,\omega_l)cos\theta_ld\omega_l \tag {35}$$

  其中$\rho$是BRDF函数，$L(\omega_l)$是面光源从$\omega_l$方向入射进来的辐射率，$P$是面光源区域。在渲染时，我们通过$(\theta_v,\alpha)$去查找预计算的纹理，得到LTC变换的$M^{-1}$矩阵，结合前面的公式$(33)$，我们有如下的近似形式：

$$\begin{align} I=&\int_{P}L(\omega_l)\rho(\omega_v,\omega_l)cos\theta_ld\omega_l\\ \approx &\int_PL(\omega_l)D(\omega_l)d\omega_l \end{align} \tag {36}$$

  这个还不是最终使用的计算公式。根据面光源的发光策略不同，这里又分为两种情况。第一种情况就是面光源的辐射率为某个固定的常量时，即$L(\omega_l)=L$，那么可以直接把$L(\omega_l)$提出积分外面：

$$I=\int_PL(\omega_l)D(\omega_l)d\omega_l=L\int_PD(\omega_l)d\omega_l \tag {37}$$

  剩余的积分公式我们直接利用LTSDs分布的性质（即前面的公式$(31)$）：

$$\int_PD(\omega)d\omega=\int_{P_o}D_o(\omega_o)d\omega_o=E(P_o) \tag {38}$$

  其中$P_o=M^{-1}P$，$D_o(\omega_o)$是前面提到的clamped cosine分布。上述中的$E(P_o)$实际上早在1989年的论文$^{[3]}$中就已经给出了其解析解，其计算公式为：

$$E(p_1,...,p_n)=\frac{1}{2\pi}\Sigma_{i=1}^n\mathbf{acos}(p_i\cdot p_j)(\frac{p_i\times p_j}{||p_i\times p_j||}\cdot \left[ \begin{matrix} 0\\ 0\\ 1 \end{matrix} \right] ) \tag {39}$$

  其中$j=(i+1)\%n$，$p_1$到$p_n$是多边形面光源的顶点。因此只考虑上半球的光照，因此还需要对多边形进行裁剪，将超出上半球的区域给剔除掉，最后再用公式$(39)$进行计算。

  以上是第一种情况即$L(\omega_l)$为固定常量的光照计算。第二种情况则是面光源通过纹理来指定各处发射的辐射率，这种情况稍微麻烦一点，因为$L(\omega_l)$不再是常量。此时我们把公式$(36)$拆成两项：

$$\begin{align} I\approx&\int_P L(\omega_l)D(\omega_l )d\omega_l=I_D I_L\\ I_D =& \int_PD(\omega_l)d\omega_l\\ I_L =& \frac{\int_P L(\omega_l) D(\omega_l)d\omega_l}{\int_P D(\omega_l)d\omega_l} \end{align} \tag {40}$$

  相比于第一种情况，我们多了一项$I_L$需要计算（$I_D$直接用前面的公式$(39)$计算）。仔细体会上面的公式，不难理解，$I_L$的计算公式可以看成是对面光源的入射辐射率进行滤波的操作。因此作者提出一种基于高斯模糊的trick来近似计算$I_L$的值，这方面的更多细节请移步原文。

  综上所述，基于LTC的实时面光源光照可以分成以下几步：

• 预计算$M^{-1}$并存储到LUT纹理中；
• 从LUT问题得到$M^{-1}$，对面光源的各个顶点进行变换；
• 对变换后的面光源进行裁剪，将超出上半球的区域剔除掉；
• 根据公式$(40)$计算光照结果。

  更多实现细节请移步这里，作者给出了相应的demo代码。

Reference

$[1]$ Background: Physics and Math of Shading by Naty Hoffman.

$[2]$ Eric Heitz, Jonathan Dupuy, Stephen Hill, and David Neubelt. 2016. Real-time polygonal-light shading with linearly transformed cosines. ACM Trans. Graph.35, 4, Article 41 (July 2016), 8 pages.

$[3]$ Baum D R, Rushmeier H E, Winget J M. Improving radiosity solutions through the use of analytically determined form-factors[J]. ACM Siggraph Computer Graphics, 1989, 23(3): 325-334.

$[4]$ GAMES202: 高质量实时渲染