高质量实时渲染：实时全局光照

WC Yang

2021-06-12

Computer Graphics / Real-time Rendering

本文是闫令琪老师GAMES202高质量实时渲染课程的学习笔记和总结，这一节的主题为实时全局光照，涉及的技术有RSM（Reflective Shadow Maps）、LPV（Light Propagation Volumes）、VXGI（Voxel Global Illumination）、SSAO（Screen Space Ambient Occlusion）、SSDO（Screen Space Directional Occlusion）以及SSR（Screen Space Reflection/Ray-tracing）。

在实时渲染领域，所谓的全局光照其实就是在直接光照的基础上再加一次bounce的间接光照（如下图1所示）。即便如此，一次bounce的间接光照也能让渲染的光影结果更为真实和炫酷。本次主题涉及的内容较多，相关的技术可以分成两类：一类为基于三维空间的方法（RSM、LPV和VOXGI），而另一类为基于屏幕空间的方法（SSAO、SSDO和SSR）。下面本文按照这个顺序依次对这些技术做一个简单的介绍和总结。

图1 one-bounce的间接光照示意图

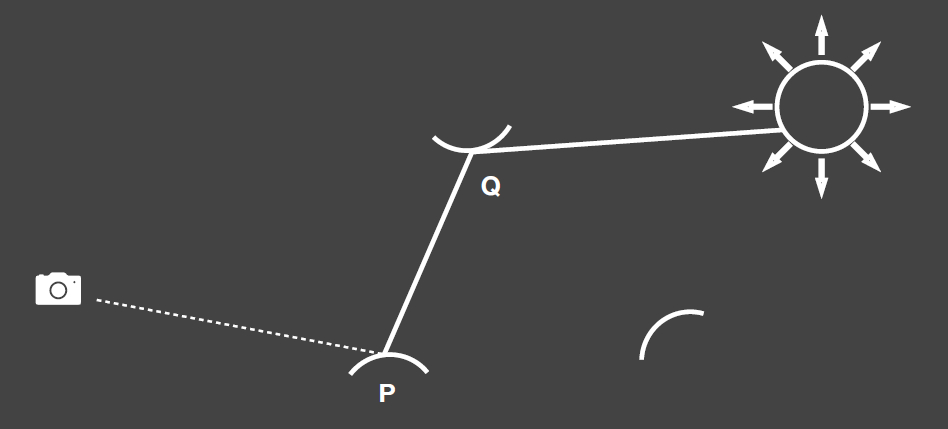
上面提及的实时全局光照算法都是多Pass的方法。这些算法的核心思路基本上都是先计算出直接光照的辐射率，然后再把直接光照的结果当作次级光源进一步计算弹射一次的间接光照效果。如下图2所示，第一个Pass计算Q点的直接光照辐射率，紧接着后续的Pass把Q当作光源并计算Q通过P反射到视点的辐射率值。这个思路贯穿了实时全局光照算法的始终。

图2 把Q点当作次级光源计算Q到P再反射到摄像机的辐射率

具体的效果见如下图3所示。可以看到，加上了一次弹射的间接光照之后，整个渲染的场景明亮了许多，显得更加真实、美观，这就是实时全局光照算法的目的所在。

图3 有无间接光照的前后效果对比

一、RSM

RSM（Reflective Shadow Maps）算法是基于Shadow Map机制的，也是两个Pass的方法。在第一个Pass，RSM算法需要记录哪些场景面元被直接光照照亮，将这些被直接光照照亮的面元几何信息和着色信息存储记录下来；在第二个Pass，根据前面得到的直接光照照亮面元的信息，计算这些面元对其他场景物体的光照。

在第一个Pass，与Shadow Map一样，RSM算法将会从光源的视角来渲染整个场景，这样就能够保证将所有能够被直接光照照亮的面元捕获并存储到贴图中。相比与Shadow Map存储深度值，RSM还会存储其他的一些信息，例如世界空间的顶点坐标、法线向量、反射通量等，如下图4所示，后面会解释为什么需要存储辐射通量。

图4 RSM第一个Pass存储的贴图信息

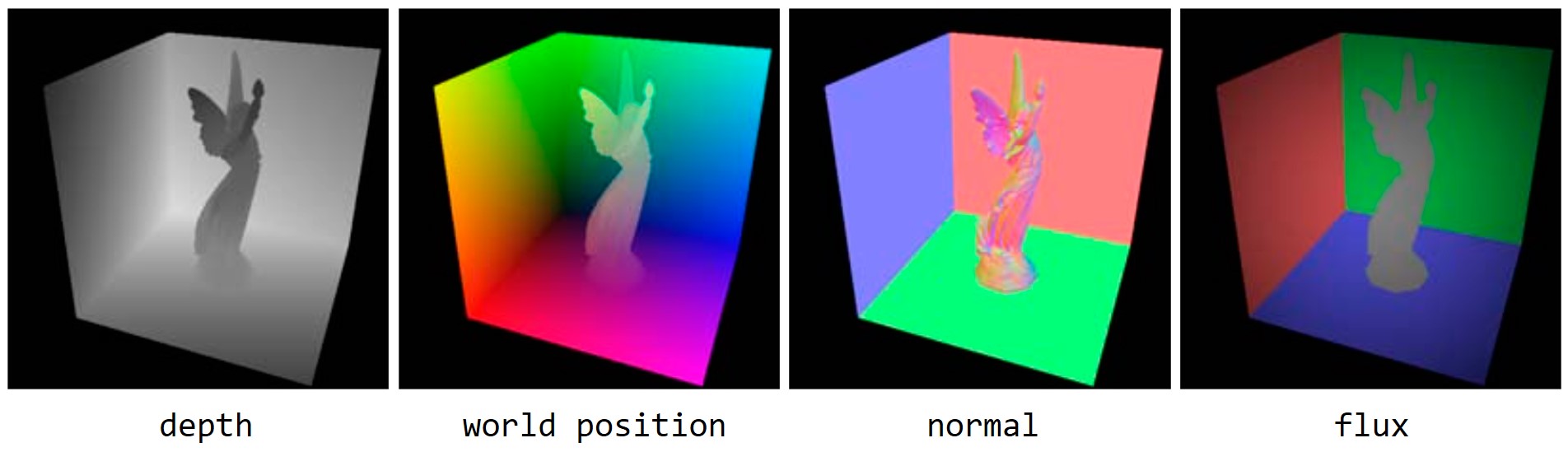
我们把这些贴图上的像素称为surface patch，即当作一个面元。在第二个Pass，RSM算法把这些surface patch当作一个面光源来看待，因此这些面元亦被称为反射物（reflector）。为了便于存储和计算reflector到任意方向的辐射率，RSM算法做了一个假设：reflector即反射物的材质均为漫反射材质，这样reflector到任意方向的反射辐射率是一个某个固定的值。

在第二个Pass，RSM算法会从摄像机的视角渲染整个场景。此时需要根据第一个Pass给定的surface patch信息做一个间接光照的计算。如下图所示，对于场景中的一点$p$，现需要计算reflector点$q$到$p$点的反射辐射率贡献，记为$L_i(q\to p)$。

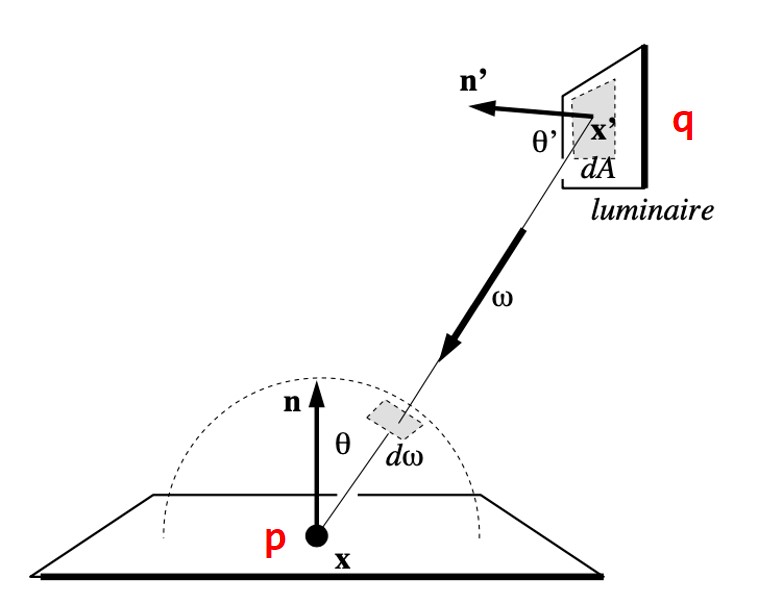
假设我们已经知道了$L_i(q\to p)$，那么$p$点向视点方向$\omega_o$的辐射率$L_o(p,\omega_o)$由以下的渲染方程给出：

$\begin{align} L_o(p,\omega_o)=&\int_{\Omega_{patch}}L_i(p,\omega_i)V(p,\omega_i)f_r(p,\omega_i,\omega_o)cos\theta_id\omega_i\\ =&\int_{A_{patch}}L_i(q\to p)V(p,\omega_i)f_r(p,q\to p,\omega_o)\frac{cos\theta_p cos\theta_q}{||q-p||^2}dA \end{align} \tag {1}$

因为现在的reflector都是以surface patch的形式给出，所以这里把渲染方程转成了对所有的面元做积分的形式。因为RSM假定reflector都是diffuse，因此$L_i(q\to p)$可以写成如下形式（结合BRDF定义）:

$L_i(q\to p)=f_r\cdot \frac{\Phi}{dA}=\frac{\rho}{\pi}\cdot \frac{\Phi}{dA} \tag {2}$

公式$(2)$中的$f_r$、$dA$和$\rho$分别为reflector的BRDF函数、面积以及反照率，而$\Phi$则是直接光源的辐射通量。把公式$(2)$带入到公式$(1)$，可以巧妙地消去$dA$项，从而有$q$点到$p$点的辐照度（Irradiance）公式：

$E_q(p,n)=\Phi_q\frac{max(0,cos\theta_p)\cdot max(0,cos\theta_q)}{||p-q||^2} \tag {3}$

其中，$\Phi_q$就是前面提到的反射通量（即图4的最后一列）。对于平行光源，其计算公式为$\Phi_q=\Phi\cdot \rho/\pi$，$\Phi$是直接光源的辐射通量，$\rho$是反射物$q$点的反照率；对于点光源，还要乘上一个余弦项（光照方向与$q$点法线夹角）。从而，$p$点接收到的所有间接光照辐照度为：

$E(p,n)=\Sigma_{q}E_q(p,n) \tag {4}$

从而，$p$点向视点反射的间接光照辐射率$L_o(p,\omega_o)$为（实际的渲染方程）：

$\begin{align} L_o(p,\omega_o)=&\Sigma_q f_r(p,q\to p,\omega_o)\cdot E_q(p,n)\\ =&\Sigma_q f_r(p,q\to p,\omega_o)\cdot \Phi_q\cdot\frac{max(0,cos\theta_p)\cdot max(0,cos\theta_q)}{||p-q||^2} \end{align} \tag {5}$

这里的$f_r$是$p$点的BRDF（请特别注意，RSM仅假定reflector是diffuse，并没有假定$p$点是diffuse，因此这里的BRDF没有任何限制）。公式$(5)$没有考虑可见性项$V$（做不了，直接不做了），因此会带来一定的artifact，但仍然还可接受。

最后一个需要解决的问题是如何选定公式$(5)$中的求和范围$\Sigma_q$，即如何从第一个Pass的贴图中选定reflector像素集合。RSM算法直接大胆假设空间上相邻的点投影到Shadow Map上也是邻近的，因此RSM采用如下的采样模式。

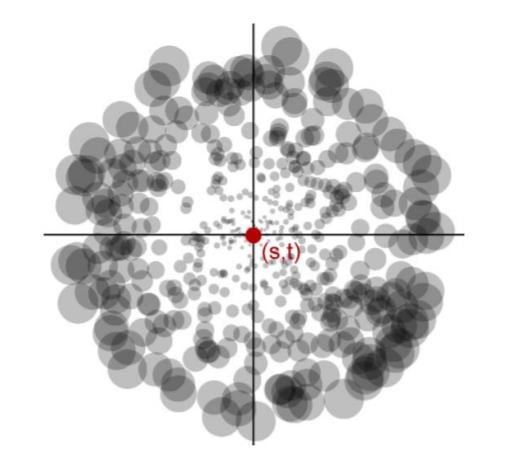
首先把$p$点投影到贴图上，记投影点为$(s,t)$；对以$(s,t)$为中心、以$r_{max}$为半径的圆内像素做一个采样，这里通过极坐标来实现，令$\xi_1$、$\xi_2$为两个均匀随机数，那么采样的像素位置为：

$(s+r_{max}\xi_1sin(2\pi\xi_2),t+r_{max}\xi_1cos(2\pi\xi_2))$

这种采样会导致距离远的地方采样密度比较稀疏，为了补偿这一点，论文$^{[1]}$将采样得到的反射辐照度值再乘上一个值$\xi_1^2$（如上图圆盘大小所示），这样最后需要再做一次归一化操作，防止能量不守恒。论文$^{[1]}$实践指出采样$400$个像素就能够取得非常好的效果。

RSM算法的优点就是实现起来非常简单，但缺点也有不少：

与Shadow Map一样，光源数量等于贴图数量；
不考虑间接光照的相互可见性，因此存在一些artifact；
做了一些大胆的假设和限定，例如要求reflector必须是diffuse;
渲染质量和贴图采样率息息相关，需要在两者之间做一个tradeoff。

关于RSM的算法就总结到这，更多细节请看论文$^{[1]}$。

二、LPV

LPV（Light Propagation Volumes）算法基于这样的一个假设：光照辐射率在三维空间中沿直线传播且传播过程中辐射率保持不变。因此，LPV的核心思路就是将整个场景的三维空间划分成一个均匀的体素网格（注意并不是将场景物体体素化），如下图所示，然后在这些体素格子之间传播光照的辐射率，最后每个着色点根据其三维位置找到相应的体素格子，从中取传播得到的辐射率进行间接光照的计算。

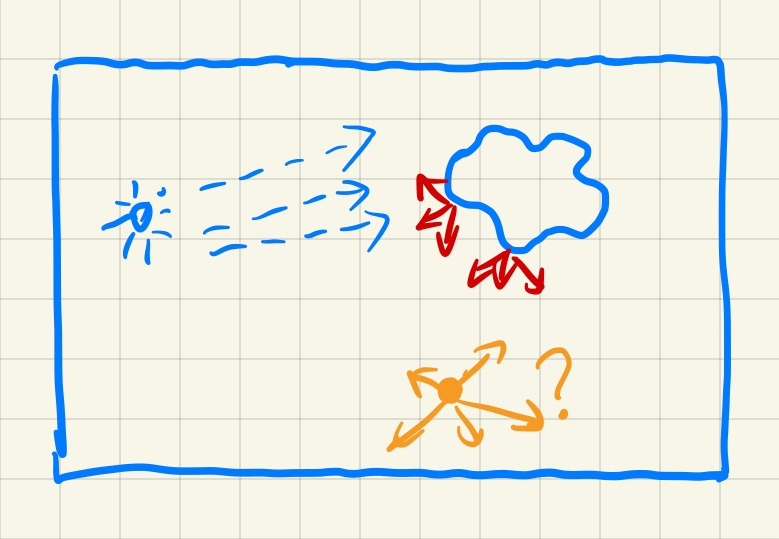
由此，LPV算法可以分成以下的四个步骤：

（1）直接光照的信息生成；
（2）将直接光照得到的虚拟光源注入到三维体素网格中；
（3）体素网格之间的辐射率扩散、传播；
（4）根据传播得到的辐射率进行间接光照的计算。

由于LPV涉及的具体细节比较多，限于篇幅，这里不会展开过多的细节描述。在步骤（1）中，LPV算法借助RSM机制，从光源的角度渲染整个场景，然后将深度信息、顶点位置、法线向量和反射通量保存到贴图纹理当中。然后在步骤$(2)$时，创建一个三维的体素网格（3D纹理），然后根据RSM贴图的信息，将有几何体的贴图像素当作一个虚拟光源，根据贴图上存储的顶点位置找到其对应的体素格子，将反射通量注入保存到这个体素格子中，从而完成虚拟光源注入的过程。

每个体素网格的中心可以看成是一个点光源。但值得注意的是，格子中心的点光源并不是向所有方向均匀辐射的！因为在注入阶段，格子中心仅仅在某些方向被注入了虚拟光源。因此，为了描述格子中心向不同方向的辐射情况，LPV采用了球面谐波函数来描述其球面方向上的辐射率分布情况。

LPV论文$^{[2]}$的作者采用了前两阶（也就是前四个）球面谐波函数来存储格子中心的辐射率分布。因此每个格子存储$4\times 3$个权重系数（乘以$3$是因为辐射率是RGB光谱）。在前一篇博客中我们提到，球面谐波权重的系数的计算公式为：

$c_i=\int_{\Omega}L(\omega)\cdot B_i(\omega)d\omega$

其中积分区域$\Omega$为球面方向，$B_i(\omega)$是第$i$个球面谐波函数，$L(\omega)$是虚拟光源向格子中心发射的辐射率，因此其取值为$L(\omega)=\Phi\cdot max(0,n\cdot \omega)$，其中$\Phi$、$n$分别是RSM贴图上的反射通量和法线向量，$\omega$是从虚拟光源到格子中心的方向向量。这个权重的计算发生在注入阶段（也就是步骤（2））。在实际的渲染场景，我们没有必要做球面的积分。这是因为$L(\omega)$分布是一个狄拉克函数，它仅仅在有虚拟光源的方向不为零，因此可以直接把积分符号去掉，转变成如下的求和公式：

$c_i=\Sigma_p L_p(\omega)\cdot B_i(\omega) \tag {6}$

即对所有落到该体素格子内部的虚拟光源做一个谐波函数权重求和，得到最终的权重系数。$L_p(\omega)$是虚拟光源$p$到格子中心的辐射率。将所有的虚拟光源注入到三维体素格子之后，步骤（3）开始在这些体素格子之间传播光照的辐射率。在此之前，我们需要知道如何复原格子中心向任意方向发射的辐射率信息。公式$(6)$计算了球面谐波的权重系数，那么对于给定的辐射方向$\omega_c$，我们可以用如下的公式复原得到格子中心向$\omega_c$发射的辐射率：

$L_(\omega_c)=\Sigma_i c_i \cdot B_i(\omega_c) \tag {7}$

步骤（3）的体素格子之间的辐射率传播采用迭代扩散的方式进行。在每一次迭代过程中，每个体素格子向与其直接相邻的格子传播辐射率（下图所示，三维情况是6个相邻格子）。依次迭代下去，直到一定的迭代次数，论文$^{[2]}$实践表明$4$次的迭代能够取得不错的效果。

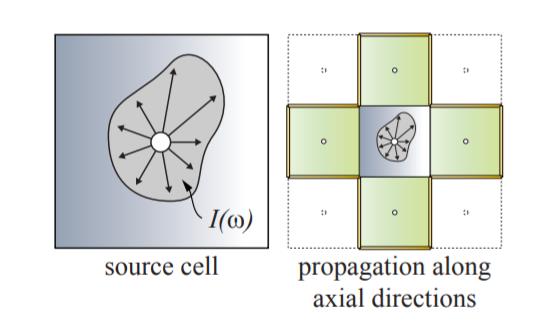
相邻格子是如何传播的呢？这里根据我的理解简单说一下，下图以二维情况为例，从左边的格子传播到右边的格子。首先将体素格子中心的辐射率传播到右边格子的$3$个非临接面上（即不包括直接相接的那个面，三维情况是$5$个面）。

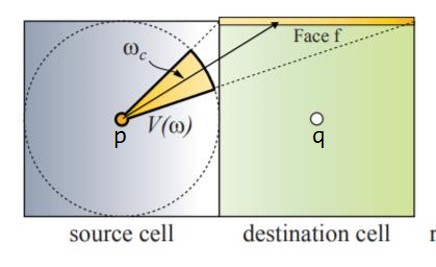
从$p$点辐射到表面$f$的辐射通量为$\Phi_f=\Delta_f/(4\pi )\cdot I(\omega_c)$，其中$\Delta _f$为表面$f$投影到以$p$为中心的立体角值（可以预先计算得到），$\omega_c$是立体角的中心方向，$I(\omega_c)$是点$p$向$\omega_c$方向发射的辐射率值，由前面的公式$(7)$计算得到。然后由表面$f$再向$q$点发射的辐射率则为$\Phi_f/\pi$。再根据前面的公式$(6)$将其展开成球面谐波权重系数，将这些权重系数加到$q$点存储的权重系数上，从而完成了一个面的传播过程。其他面的计算过程类似。对于三维情况，相邻格子需要完成$5$个面的辐射率传播。

最后的步骤（4）其实不言自明。在计算过程的时候，找到着色点对应的体素格子，从中取出球面谐波的权重系数，根据公式$(7)$还原出给定方向上的辐射率，完成间接计算的过程。这里有一个LPV的实现参考代码。LPV的问题主要是会产生漏光的artifact，而且如果三维体素格子如果划分得太过粗糙，那么实现的光照效果会有明显的块状artifact，比较难看。

三、VXGI

VXGI（Voxel Global Illumination）与RSM算法一样，也是两个Pass的方法。目前基于体素的全局光照方法有两类，除了VXGI，还有Sparse Voxel Octree GI（简称SVOGI）。VXGI和SVOGI主要的区别在于使用的存储数据结构不同，SVOGI使用稀疏体素的八叉树结构来管理场景的体素，而VXGI则采用Clipmap机制。对于动态的场景，两种方法都要在物体发生动态变化时重建（或者说调整）场景的数据结构。基于Clipmap的VXGI算法可以看成是SVOGI的优化，它在构建数据结构时更为简单，而且内存效率方面更具优势，因此这里不对SVO做介绍。

VXGI的场景体素化借用了光栅化的渲染机制，将场景物体分别在$x$、$y$和$z$轴三个方向上投影绘制三次，这个我在之前的一篇博客记录过，因此这里不再赘述。VXGI会创建一些3D纹理，场景体素化之后会将场景物体的颜色值、法线向量、自发光信息、阴影遮挡信息、粗糙度等存储到这些3D纹理中。需要注意的是，在体素化时，有可能不同的三角形面片会被体素化到同一个体素格子，因此体素格子的属性信息是所有落在这个体素内的三角形属性的平均值。

生成了3D体素纹理之后，紧接着的步骤是直接光照的Pass。直接光照Pass可以直接借用RSM机制来实现，即从光的视角来渲染整个场景，将直接光照的数据存储到贴图中，然后再将贴图里面的直接光照数据注入到场景体素化的3D纹理当中。然后再为这些3D纹理生成Mipmap，如下图所示（Clipmap本质上就是在Mipmap的基础上加了个裁剪范围，使得显存只需要加载每个Mipmap层次的一部分，这里不细说）。

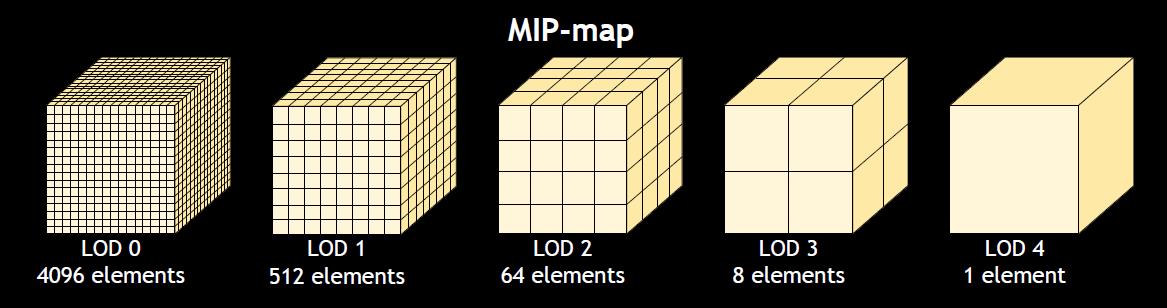
间接光照Pass是从摄像机的角度渲染整个场景，并根据上面的Mipmap结构对场景发射射线进行追踪来计算间接光照部分。这里发射追踪的射线是具有一定角度的圆锥体。但圆锥体也并不是真正意义上的圆锥体，而是由不同level的体素拼接而成的类锥体的形状，如下图所示，从近到远，体素的大小逐渐增大。

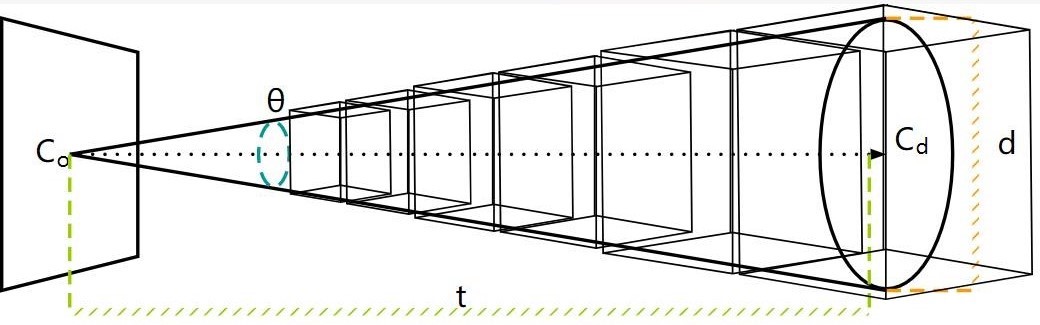
记tracing的圆锥体起始点为$C_0$、方向为$C_d$、圆锥体的角度为$\theta$、当前追踪的长度为$t$，那么可以用以下的公式计算出当前的ray marching点所在体素的边长（仔细观察上图，不难理解）：

$d=2t \cdot tan(\frac{\theta}{2}) \tag {8}$

而后可以通过$d$计算出需要在哪个level的Mipmap上进行采样：

$level=log_2(\frac{d}{V_{size}}) \tag {9}$

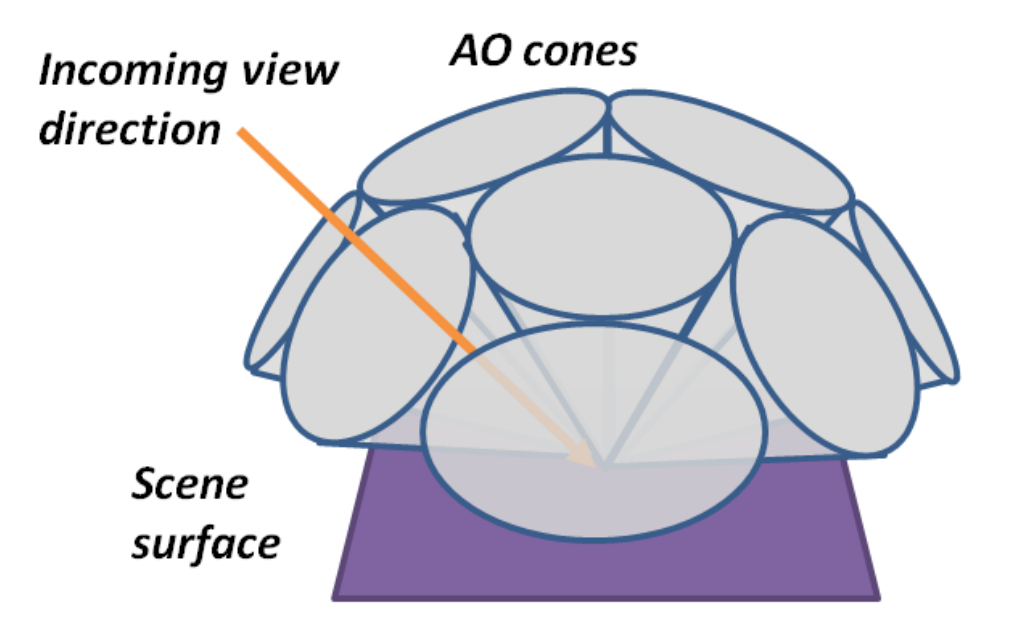
其中，$V_{size}$是Mipmap最高level的大小（即最粗糙层级的Mipmap边长）。以上是一个tracing cone做光线步进。针对不同的材质，VXGI会发射不同数量的tracing cone进行间接光照的计算。对于glossy材质，VXGI只发射一个tracing cone，并通过调整锥形的角度来实现不同粗糙度下的glossy反射效果（越粗糙锥形角度越大）；对于diffuse材质，VXGI发射多个tracing cone（如下图所示），这些tracing cone基本覆盖了法线朝向的半球方向，从而近似实现对半球方向的积分。锥形的数量可以调整，越多越精确，但考虑到效率问题，一般也就$5$到$8$个。

VXGI可以实现非常惊艳的全局光照效果，但是它的缺点也显而易见：3D纹理太过耗费显存，体素化的精度决定了光照精度，而且也存在一些漏光的artifact现象。这里给出了一个非常不错的VXGI实现，可以参考参考。

四、SSAO

SSAO（Screen Space Ambient Occlusion）本质上也是为了实现间接光照导致的光照强弱分明效果（在一些角落、拐角或者隐蔽的地方由于互相遮挡光照强度较弱），这种效果我们称之为环境光遮蔽。这种环境光遮蔽的效果能够大大地增强场景的光影层次感，使得渲染出来的效果更具三维立体感，下图给出了有无AO的效果对比。

SSAO首先做了如下的假设：

场景中所有物体接收到的来自各个方向的间接光照为指定常量值（类似于Phong光照模型里面的ambient项）
在计算场景物体的AO项，把场景中需要计算可见性项的物体的材质当作diffuse来看待

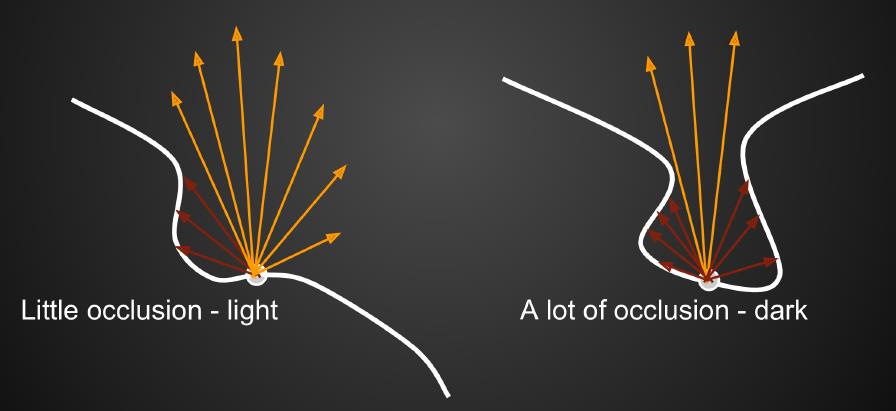
这里的AO（Ambient Occlusion）就是衡量着色点接收到间接光照的量，如下图5所示。在半球方向内，如果存在的遮挡物比较多，那么该着色点接收到间接光照量就少，因而比较暗；反之则比较亮。

图5 Ambient Occlusion

下面简单总结一下SSAO的理论。首先从间接光照的渲染方程出发：

$L_o^{indiect}(p,\omega_o)=\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)V(p,\omega_i)cos\theta_id\omega_i \tag {10}$

结合前面提到的SSAO假设，上式中的$L_i(p,\omega_i)$为指定的某个常量值，BRDF函数$f_r(p,\omega_i,\omega_o)$为diffuse。在RTR领域，有如下的近似公式：

$\int_{\Omega}f(x)g(x)dx\approx \frac{\int_{\Omega_G}f(x)dx}{\int_{\Omega_G}dx}\cdot \int_{\Omega}g(x)dx$

这个近似公式在之前的博客已经提到过，不再赘述。把公式$(10)$按照上面的近似公式进行拆分：

$\begin{align} L^{indirect}_o(p,\omega_o)\approx &\frac{\int_{\Omega^+}V(p,\omega_i)cos\theta_id\omega_i}{\int_{\Omega^+}cos\theta_id\omega_i}\cdot\\ &\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)cos\theta_i d\omega_i \tag {11} \end{align}$

上面的公式把$cos\theta_i d\omega_i$看作一个整体（即看成一个整体的积分变量），把可见性项$V(p,\omega_i)$单独拿出来。又因为$L_i$是指定的常量，$f_r$是diffuse材质的，即$f_r=\frac{\rho}{\pi}$，这两个都可以直接提到积分符号外面，所以上面的公式可以进一步简化为：

$\begin{align} L^{indirect}_o(p,\omega_o)\approx&\frac{\int_{\Omega^+}V(p,\omega_i)cos\theta_id\omega_i}{\pi}\cdot L_i(p,\omega_i)\cdot \frac{\rho}{\pi}\cdot \pi\\ \approx&\frac{\int_{\Omega^+}V(p,\omega_i)cos\theta_id\omega_i}{\pi}\cdot L_i(p,\omega_i)\cdot \rho \end{align} \tag {12}$

其中$\rho$就是着色点的反照率。上面的$\int_{\Omega^+}V(p,\omega_i)cos\theta_id\omega_i/\pi$就是AO项，公式$(12)$就是SSAO的核心公式。现在的关键问题就是如何求解AO项的可见性积分$\int_{\Omega^+}V(p,\omega_i)cos\theta_id\omega_i$。SSAO在屏幕空间对AO项积分近似求解。所谓的基于屏幕空间的方法，其实就是后处理方法，因此也是两个Pass。第一个Pass从摄像机角度渲染场景并存储着色点的属性到G-buffer中（深度、顶点、Albeod等）；第二个Pass渲染屏幕空间大小的四边形，根据G-buffer的信息做进一步的处理，从而得到最终的结果。

在第二个Pass，SSAO获取G-buffer上的顶点$p$，在以$p$点为球心的球体内部播撒一些采样点（这些采样点也是三维的）。对于每一个采样点$q$，可以通过投影矩阵得到其深度值，将该深度值与$q$点对应的深度贴图上的值进行比较，如果采样点的深度值小于深度贴图上的深度值，那么这个采样点就是可见的（如下图6的绿点），反之则是不可见的（如下图6的红点）。

图6 SSAO的计算

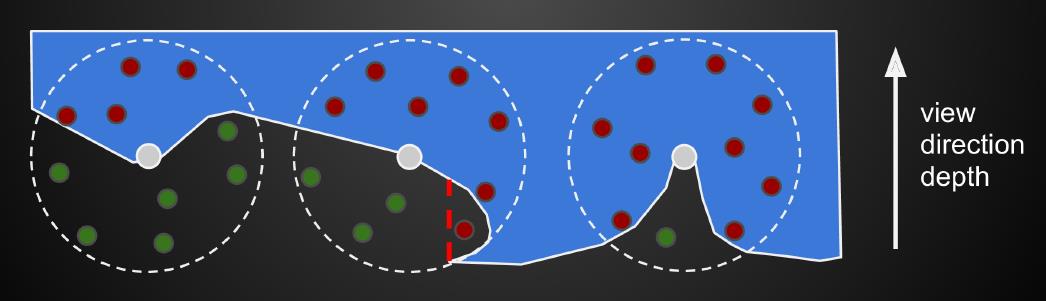
最后的AO值就是绿色点数量除以总的采样点数量。这种方法并非物理准确的，例如上图6中间球体最下面的那个小红点，但无伤大雅。在实际的实践中，仅当红点数量过半的时候，才会考虑AO项，否则不考虑AO，这是为了弥补公式$(12)$积分项的半球积分范围（而非球体范围）。SSAO的缺点主要是它在容易在前后不同物体重叠的地方产生了AO现象，这是一个artifact。针对这个问题，一些学者对SSAO进行了改进——提出了HBAO（Horizon Based Ambient Occlusion），HBAO在采样时结合了法线在半球内进行采样。

五、SSDO

SSDO（Screen Space Directional Occlusion）是SSAO的进一步改进。SSAO假设着色点接收到的$L_i$是某个给定的常量值，因此它的AO效果仅仅是变暗。为了产生间接光照的颜色溅射效果，SSDO算法应运而生。同样的，也是两个Pass，而SSDO也主要是在第二个Pass进行处理。如下图所示，SSDO主要考虑下图中的黑色射线打到间接光照效果（而SSAO反过来，考虑通过黄色射线来计算可见性）。

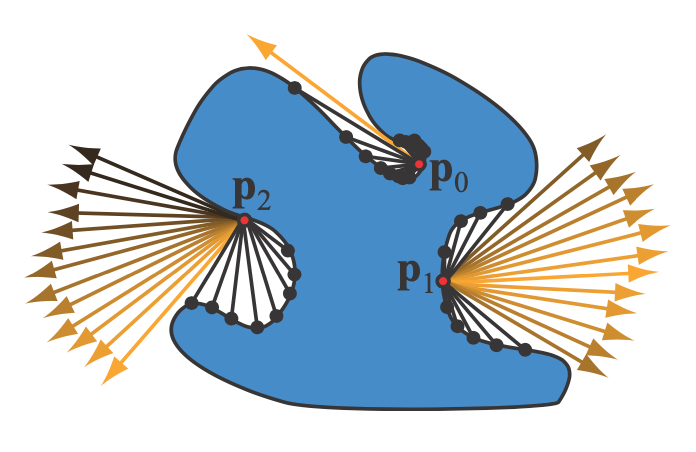
由此，SSDO的核心理论是如下的两个公式：

$\begin{align} L_o^{dir}(p,\omega_o)=&\int_{\Omega^+\ V=1}L_i^{dir}(p,\omega_i)f_r(p,\omega_i,\omega_o)cos\theta_i d\omega_i\\ L_o^{indir}(p,\omega_o)=&\int_{\Omega^+\ V=0}L_i^{indir}(p,\omega_i)f_r(p,\omega_i,\omega_o)cos\theta_id\omega_i \end{align} \tag {13}$

上述公式分为两部分，分别是直接光照和间接光照。其中$V=1$表示射线$\omega_i$击中了场景中的其他物体，反之则没有击中。实际上就是把半球的积分区域分成了两部分，结合上图示例，对于黄色射线部分我们计算直接光照部分（当然一般不需要积分，这里仅仅是为了理论严谨），对于黑色射线部分我们计算间接光照部分。因此重点在于公式$(13)$的第二个公式如何计算。

与SSAO类似，SSDO从G-buffer取出着色点的顶点和法线，然后在在法线朝向半球范围内播撒采样点，如下图7最左边的图片所示的A、B、C和D点。然后对于每一个采样点$p$，对比该采样点的深度与该采样点对应到的深度贴图上的深度，如果采样点被遮挡了（深度值大于贴图上的深度值），那么就计算遮挡位置的直接光照信息，加到$p$点的间接光照上，如下图7的中间图片所示（例如A点对应的橙色点）。这就是SSDO的算法思想。

图7 SSDO的计算

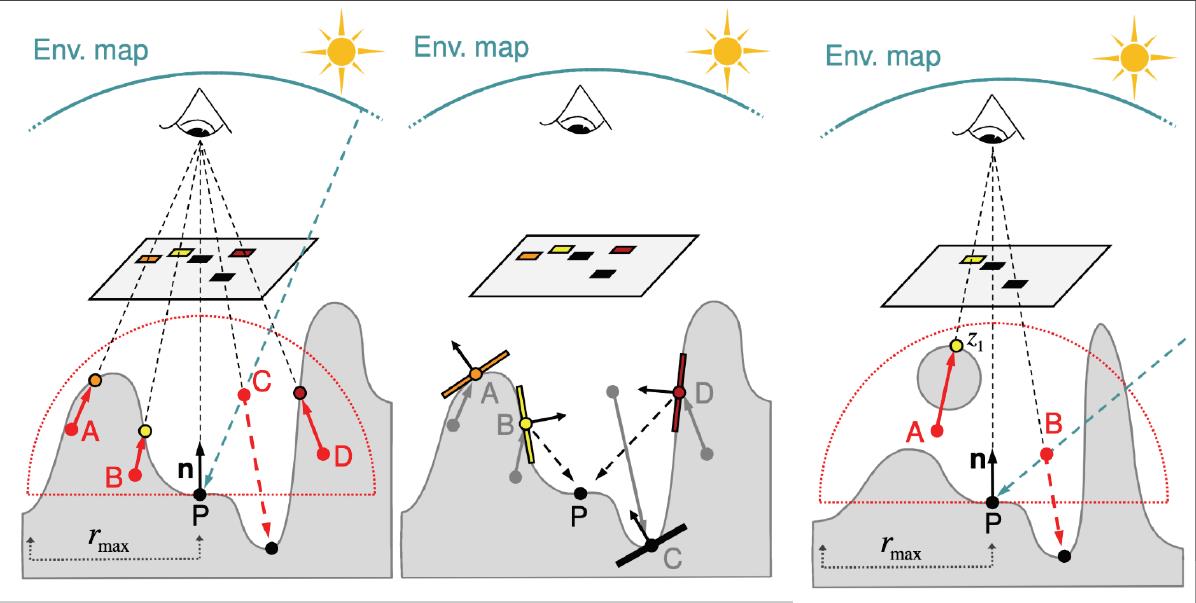
这种近似的求解当然也不是物理准确的，例如上图7的最右边图片所示，A点对应的$z_1$点并不会对$p$点产生间接弹射的贡献。而且值得一提的是，采样的半球半径限制了弹射范围，只有在半球半径范围内的点才会被考虑进来，因此不会渲染超过一定范围内的间接弹射效果。最后需要注意的就是，SSDO是基于屏幕空间的，因此它所有的间接光照信息都来源于当前摄像机能够看到的，对于那些看不到的面元，自然也就不会贡献间接光照的效果。

六、SSR

与前面的SSAO和SSDO，SSR（Screen Space Ray-tracing/Reflection）同样也是基于两个Pass的。在渲染了第一个Pass的G-buffer之后，SSR尝试根据G-buffer提供的信息找到给定着色点接收的间接光照。SSR并不仅仅局限于镜面反射，对于glossy和diffuse，SSR也可以做间接光照的追踪，因此用Screen Space Ray-tracing来命名更为合适。

SSR的核心思路就是追踪当前屏幕空间已有的信息，如上图所示，地面反射的光影效果在当前屏幕上已经存在，因此可以直接进行追踪。事实上，G-buffer存储的深度值可以看成从摄像机角度的SDF（符号距离场），可以近似地当成一种对场景的SDF描述。由此，SSR尝试在屏幕空间上做光线步进（Ray Marching）来找到光线与场景的交点。找到交点之后，根据交点的法线、顶点、反照率等得到交点处的直接光照辐射率，以此作为弹射的间接光照辐射率，从而实现间接光照。

图8 SSR算法

SSR针对不同的材质发射不同数量的追踪光线。对于完美specular的材质，发射一条反射光线；对于glossy的材质，根据glossy材质的粗糙度来计算反射的lobe，在lobe范围内发射一些采样光线；对于diffuse的材质，在半球范围内发射采样的光线。总的来说，对于每一个片元，SSR分为以下三步：

根据当前片元的顶点、法线，计算反射的采样光线；
从片元的顶点出发，沿着采样的光线进行光线步进（通过深度缓冲来判断是否发生了相交）；
如果找到了交点，使用交点处的直接光照效果作为反射颜色；如果步进超过一定的距离（或超出屏幕空间范围）仍没有交点，那么终止步进。

第二步的每一次光线步进，我们都会做一次相交判断。相交判断的逻辑为：将当前的步进点$p$的深度值与$p$点对应的深度贴图上的深度值进行大小判断，如果$p$点的深度值大于深度图贴图上的深度值，那么就说明当前步进的点落到某个场景表面之下，这时就发生了相交。最为Naive的光线步进就是Linear Ray-marching，也就是每次步进一小段固定的距离，如下代码所示：

bool RayMarch(vec3 ori, vec3 dir, out vec3 hitPos) 
{
      const float step = 0.5;
      vec3 p = ori + dir * step;
      for(int i = 0;i <= 50; ++i)
      {
          vec2 uv = GetScreenCoordinate(p);
          //out of range
          if(uv.x < 0.0 || uv.x > 1.0 || uv.y < 0.0 || uv.y > 1.0)
              break;
          float pd = GetDepth(p);
          float dd = GetGBufferDepth(uv);
          if(pd > dd)
          {
              hitPos = p;
              return true;
          }
          p += dir * step;
      }
    return false;
}

上面的光线步进是在三维世界空间做的，所以每一次都要把步进的点投影到屏幕上。但是在三维空间做固定长度的光线步进，投影到屏幕上步进的间隔并非均匀的。如下图9所示，三维空间的Linear Ray-marching会出现两个问题，分别是遗漏采样和重复采样（越红代表重复采样的次数越多）。

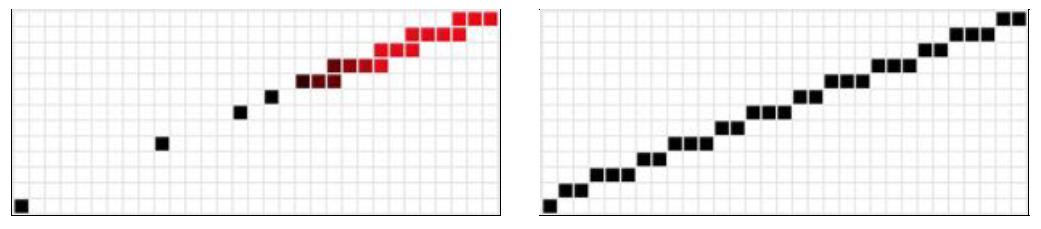
图9 三维空间（左）vs屏幕空间（右）Linear Ray-marching

因此，最为理想的情况下当然希望在屏幕空间上实现Linear Ray-marching，不浪费每一次的纹理采样。论文$^{[3]}$提出了基于DDA画线的屏幕空间Ray-marching方法，其本质上就是把三维空间的射线投影到屏幕上，在屏幕上按照固定的步长进行步进。论文$^{[3]}$借助基于DDA的直线光栅化（如图9右）来实现屏幕空间的固定步长的Ray-marching。屏幕空间的Ray-marching需要解决深度的透视纠正的问题，即每步进一定步长的像素之后，我们需要得到步进点像素对应的三维深度值（不是深度贴图上的深度值），这个其实在光栅化线性插值已经解决了，只需将深度值乘以投影之后的$w$。更多细节阅读原文，这里贴一下代码。

bool RayMarch(vec3 ori, vec3 dir, out vec3 hitPos) 
{
      const float nearPlaneZ = -0.001;
    const float maxSteps = 50.0;
    const float maxRayTraceDistance = 50.0;
    float stride = 3.0 * max(1.0/uWidth, 1.0/uHeight);
    const float jitterFraction = 1.0;
    const float csZThickness = 0.0;

    // Transform into camera space 
    vec3 csOrigin = vec3(vViewMatrix * vec4(ori, 1.0));
    vec3 csDirection = normalize(vec3(vViewMatrix * vec4(dir, 0.0)));

    // Clip ray to a near plane in 3D
    float rayLength = ((csOrigin.z + csDirection.z * maxRayTraceDistance) > nearPlaneZ) ? 
                    (nearPlaneZ - csOrigin.z) / csDirection.z : maxRayTraceDistance;
    vec3 csEndPoint = csOrigin + csDirection * rayLength;

    // Project into screen space
    vec4 H0 = vProjectMatrix * vec4(csOrigin, 1.0);
    vec4 H1 = vProjectMatrix * vec4(csEndPoint, 1.0);
    float k0 = 1.0 / H0.w;
    float k1 = 1.0 / H1.w;

    // Switch the original points to values that interpolate linearly in 2D
    vec3 Q0 = csOrigin * k0; 
    vec3 Q1 = csEndPoint * k1;

    // Screen-space endpoints
    vec2 P0 = vec2(H0.xy * k0) * 0.5 + 0.5;
    vec2 P1 = vec2(H1.xy * k1) * 0.5 + 0.5;

    vec2 hitPixel = vec2(-1.0, -1.0);

    // If the line is degenerate, make it cover at least one pixel
    // to avoid handling zero-pixel extent as a special case later
    P1 += vec2((dot(P0 - P1, P0 - P1) < 0.0001) ? 0.01 : 0.0);

    vec2 delta = P1 - P0;

    // Permute so that the primary iteration is in x to reduce
    // large branches later
    bool permute = false;
	if (abs(delta.x) < abs(delta.y)) 
    {
		// More-vertical line. Create a permutation that swaps x and y in the output
		permute = true;
        // Directly swizzle the inputs
		delta = delta.yx;
		P1 = P1.yx;
		P0 = P0.yx;        
	}

    // From now on, "x" is the primary iteration direction and "y" is the secondary one
    float stepDirection = sign(delta.x);
    float invdx = stepDirection / delta.x;
    vec2 dP = vec2(stepDirection, invdx * delta.y);

    // Track the derivatives of Q and k
    vec3 dQ = (Q1 - Q0) * invdx;
    float dk = (k1 - k0) * invdx;

    // Scale derivatives by the desired pixel stride
	dP *= stride; 
    dQ *= stride; 
    dk *= stride;

    // Offset the starting values by the jitter fraction
	P0 += dP * jitterFraction; 
    Q0 += dQ * jitterFraction; 
    k0 += dk * jitterFraction;

    // Slide P from P0 to P1, (now-homogeneous) Q from Q0 to Q1, and k from k0 to k1
    vec3 Q = Q0;
    float k = k0;

	// We track the ray depth at +/- 1/2 pixel to treat pixels as clip-space solid 
	// voxels. Because the depth at -1/2 for a given pixel will be the same as at 
	// +1/2 for the previous iteration, we actually only have to compute one value 
	// per iteration.
	float prevZMaxEstimate = csOrigin.z;
    float stepCount = 0.0;
    float rayZMax = prevZMaxEstimate, rayZMin = prevZMaxEstimate;
    float sceneZMax = csOrigin.z + 1e4;

    // P1.x is never modified after this point, so pre-scale it by 
    // the step direction for a signed comparison
    float end = P1.x * stepDirection;

    // We only advance the z field of Q in the inner loop, since
    // Q.xy is never used until after the loop terminates.
    vec2 P = P0;
    for(int i = 0;i < int(maxSteps); ++i)
    {
        if(P.x < 0.0 || P.x > 1.0 || P.y < 0.0 || P.y > 1.0)
        {
            break;
        }

        if(!(((P.x * stepDirection) <= end) && 
             ((rayZMax < sceneZMax - csZThickness) ||
              (rayZMin > sceneZMax)) &&
             (sceneZMax != 0.0)))
        {
            break;
        }

        hitPixel = permute ? P.yx : P;
        // The depth range that the ray covers within this loop
        // iteration.  Assume that the ray is moving in increasing z
        // and swap if backwards.  Because one end of the interval is
        // shared between adjacent iterations, we track the previous
        // value and then swap as needed to ensure correct ordering
        rayZMin = prevZMaxEstimate;

        // Compute the value at 1/2 pixel into the future
        rayZMax = (dQ.z * 0.5 + Q.z) / (dk * 0.5 + k);
        prevZMaxEstimate = rayZMax;

        if (rayZMin > rayZMax) 
        { 
            // Swap
            float tmp = rayZMin;
            rayZMin = rayZMax;
            rayZMax = tmp;
        }

        // Camera-space z of the background
        sceneZMax = -texture2D(uGDepth, hitPixel).r;

        P += dP, Q.z += dQ.z, k += dk, stepCount += 1.0;
    }

    Q.xy += dQ.xy * stepCount;
    hitPos = Q * (1.0 / k);

    return (rayZMax >= sceneZMax - csZThickness) && (rayZMin <= sceneZMax);
}

关于Linear Ray-march的优化，闫老师提到了基于深度贴图Mip-map的方法，这里偷懒就不说了。SSR的问题源自于它是基于屏幕空间的，屏幕空间的几何信息并不能完全表示整个场景。因此，SSR反射的间接光照信息都是目前屏幕空间上存在的，超出屏幕之外（或者被遮挡）的间接光照无法捕获。所以仔细观察下图SSR实现的效果，地面反射出来的手是不完整的。（基本上基于屏幕空间的方法，都会有这个问题）

Reference

$[1]$ Carsten Dachsbacher and Marc Stamminger. 2005. Reflective shadow maps. In Proceedings of the 2005 symposium on Interactive 3D graphics and games (I3D ‘05). Association for Computing Machinery, New York, NY, USA, 203–231.

$[2]$ Anton Kaplanyan and Carsten Dachsbacher. 2010. Cascaded light propagation volumes for real-time indirect illumination. In Proceedings of the 2010 ACM SIGGRAPH symposium on Interactive 3D Graphics and Games (I3D ‘10). Association for Computing Machinery, New York, NY, USA, 99–107.

$[3]$ Morgan McGuire and Michael Mara, Efficient GPU Screen-Space Ray Tracing, Journal of Computer Graphics Techniques (JCGT), vol. 3, no. 4, 73-85, 2014

$[4]$ GAMES202: 高质量实时渲染