本文是闫令琪老师GAMES202高质量实时渲染课程的学习笔记和总结，这一节的主题为高质量实时环境光照，内容分为IBL（Imaged Based Lighting）和PRT（Precomputed Radiance Transfer）。

一、前言

  环境光照处理着色点与周围环境的光影交互，对增强物体与周围环境的融入程度有着至关重要的作用。在实时渲染领域，环境光特指由预先生成的环境贴图提供的光照信息（即天空盒），贴图的每个纹素都可以看成是一个光源（注：这些光源我们当成其在无穷远处），因此其覆盖的方向是三维空间的所有方向。

  理论上，准确求解环境光照需要计算如下的半球积分渲染方程：

  其中，我们不考虑可见性遮挡因素，因此上式是去掉了$V(p,\omega_i)$项的。$L_i(p,\omega_i)$项通过用$\omega_i$对环境贴图进行采样获得。公式$(1)$的求解可以采用蒙特卡洛积分的方法结合重要性采样来进行求解，但这是离线渲染的做法，虽然理论上能够收敛到无偏的结果，但其耗费的算力代价和采样数量对于实时渲染来说根本不可接受！

  由此衍生了一些快速的近似求解算法，例如IBL和PRT。这些算法的核心本质，就是预计算，通过某种方法把积分的求解放在预计算阶段，并将结果存储下来，在绘制阶段直接查表来实现快速的环境光渲染。

二、Imaged Based Lighting

  IBL的本质就是Split Sum，把公式$(1)$的渲染方程进行拆解，达到变量降维的目的，实现低量存储、高速查表的性能。回顾上一节实时软阴影，我们提到实时渲染领域非常常用的一个近似公式：

  该公式把两个函数乘积的积分近似为各自积分的乘积（即把乘积符号和积分符号做了个交换）。上次我们也提到，当函数$g(x)$满足以下两个条件时，公式$(2)$的近似是相对比较准确的：

  • 当$g(x)$在积分域$\Omega$内的实际贡献（support）很小，即$g(x)$在$\Omega$内绝大部分取值为零，例如一个脉冲函数，仅在$x=0$不为零，其他地方均为零（即狄拉克函数）；
  • 当$g(x)$在积分域$\Omega$内变化不大，可以理解为低频函数。

  在实时渲染领域，有三种常用的BRDF材质：specular、diffuse和glossy，其中glossy是介于specular和diffuse之间的一种材质。三者的区别在于反射波瓣（lobe）的分布。如下图1所示，glossy的反射波瓣通常比较狭长（而specular则直接是一个方向了，其BRDF函数为狄拉克函数），diffuse反射波瓣在半球方向均匀分布。

图1 glossy（左）和diffuse（右）的反射波瓣分布

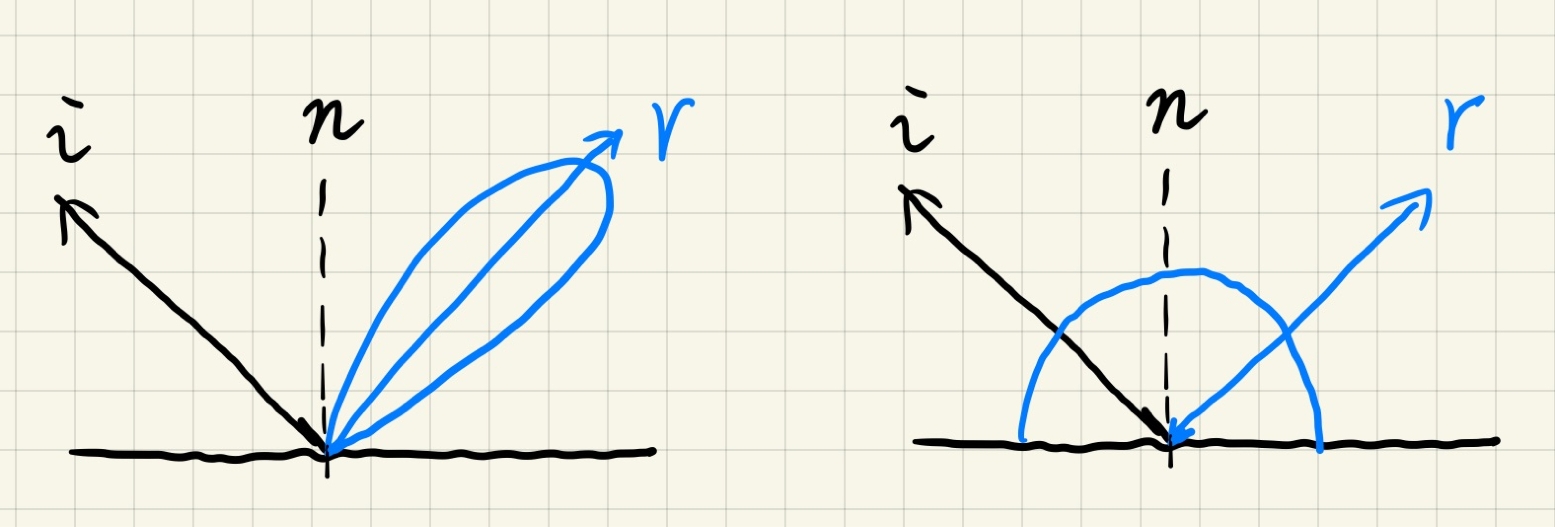
  因此，渲染方程$(1)$中的BRDF函数$f_r$在通常情况下，要么实际贡献范围很小（例如glossy），要么实际变化不大（例如diffuse）。由此可以利用公式$(2)$的近似模式来将渲染方程$(1)$拆解开来：

  近似结果拆解成了如上所示的两项，为了方便论述，我们分别称左右两项为irradiance项和brdf项。由此，IBL的预计算分成两步，分别是irradiance项的预计算和brdf项的预计算。

  irradiance项的预计算核心公式为：

  其中的积分区域$\Omega_{f_r}$为材质BRDF波瓣分布的区域。例如diffuse的话，那么就是整个半球；而对于glossy材质，其表面越粗糙，则$\Omega_{f_r}$越大。上式本质上可以看成为在$\Omega_{f_r}$区域上的对$L_i$做box filtering处理过程，不同的BRDF材质区别仅在于滤波区域$\Omega_{f_r}$的大小，材质越接近diffuse，那么其滤波范围越大，滤波得到的结果越模糊，反射的结果越模糊，反之则越光滑，这与我们的常识相符。

图2 split sum的irradiance项近似

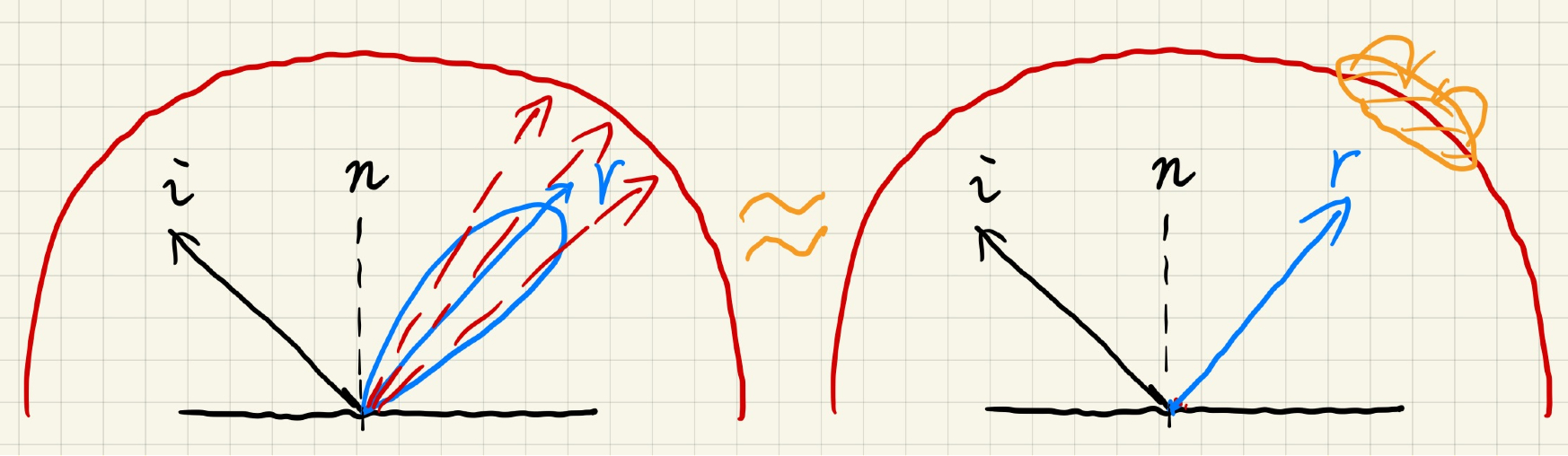
  如上图2所示，对于反射波瓣范围内的radiance采样，可以近似为该反射波瓣投影到球面上的范围内的卷积滤波处理，这就是irradiance预计算的核心本质。实现也很简单，直接用Mipmap为环境贴图生成不同level的降采样结果（降采样本质上就是一个模糊滤波），这一阶段我们称之为Pre-Filterd Evnvironment Map。然后在查表时，根据材质的粗糙度去获取采样相应level的环境贴图，查表输入的采样向量为反射向量（对于diffuse则为表面法线）。粗糙度介于不同的level之间可以再做一次插值。

  brdf项的预计算核心公式为：

  这个项的预计算不太好处理。在PBR材质流程管线，我们通常用如下的基于微表面的BRDF函数：

  其中$F$、$G$和$D$分别是菲涅尔方程、几何遮蔽函数和法线分布函数。其中$h$是介于$\omega_i$和$\omega_o$之间的半角向量（half vector）。菲尼尔方程采用Schlick近似：

  可以看到菲涅尔项依赖的参数有基础反射率$R_0$和$\omega_o\cdot h$。而$G$和$D$函数的可选项有很多，这里不罗列出来，但我们直到这两个函数依赖的参数为表面的粗糙度$\mu$。预计算的公式依赖的参数有三个，这说明我们需要三维的纹理来存储结果，为了降低依赖的维度，这里设法将一些变量提出积分符号外：

  把公式$(5)$带入公式$(6)$，有：

  然后把公式$(7)$得到的结果写成以下的两个部分：

  这样我们就把$R_0$提出积分符号外面，其中下面的$f_r$是去掉了菲涅尔项的BRDF函数。剩下的两个积分项分别依赖于粗糙度$\mu$和$n\cdot \omega_o$，我们构建这样的一个查找表，横坐标$u$为$n\cdot \omega_o$，纵坐标$v$为$\mu$，每个$(n\cdot \omega_o,\mu)$对应的纹素的r通道和g通道分别存储公式$(8)$的左右两个积分项。如下图所示：

图3 brdf积分查找表

  关于IBL的实现详情见之前的博文实时渲染Real-time Rendering：Image Based Lighting，这里不再赘述。IBL缺点在于难以处理阴影遮挡问题，目前工业界主流的方法是为cubemap最亮的区域生成一个主要的阴影。

三、Precomputed Radiance Transfer

  PRT涉及的数学内容较多，这里仅仅就个人理解做一个总结。PRT把渲染方程的辐射率项$L_i$和BRDF项展开成以球面谐波函数为基的系数权重，因此其预计算都是如何将函数投影到球面谐波函数表达的空间。

  在高等数学、数学分析等课程中，我们都曾学习过函数的级数展开（例如泰勒展开）。对于给定的一个函数$f(x)$，我们可以对其进行级数展开，表示成一系列基函数的加权之和：

  其中$B_i(x)$是第$i$个基函数，$c_i$是相应的权重。我们可以类比线性代数，把所有的基函数$B_i(x)$构成的空间看成是一个函数空间，$c_i$相应地就是在$B_i(x)$基底下的投影权重，所有的基底乘上相应的系数权重，线性组合成了原始函数$f(x)$。因此求解权重系数的过程我们称之为投影。

  以傅里叶变换为例。傅里叶变换本质上就是傅里叶级数展开过程中的投影，傅里叶级数用一系列不同频率、振幅的正余弦波的线性组合还原出原始函数$f(x)$。我们透过傅里叶权重可以更加方便地分析原始函数$f(x)$频率分布情况，进行傅里叶分析、滤波等操作。

  卷积定理告诉我们，在空间域的卷积滤波等价于在频率域的乘积。因此，对于两个函数乘积的积分：

  我们可以将上述的公式理解为低通滤波操作。滤波的结果取决于两个函数中比较低频的函数，这样较低频的函数把另一个较高频函数的高频信息过滤掉了！这个公式对于理解PRT非常重要。

  球面谐波（Spherical Harmonics，简称SH）基函数是一组定义在球面上基函数，下图4展示了前4阶的SH基函数分布。第$i$阶SH基函数有$2i+1$个，前$i$阶一共有$(2i+1)^2$个SH基函数。与一维的傅里叶级数类似，越高阶的SH基函数其蕴含的频率信息越高。每个SH基函数由伴随勒让德多项式给出。

图4 前4阶球面谐波基函数

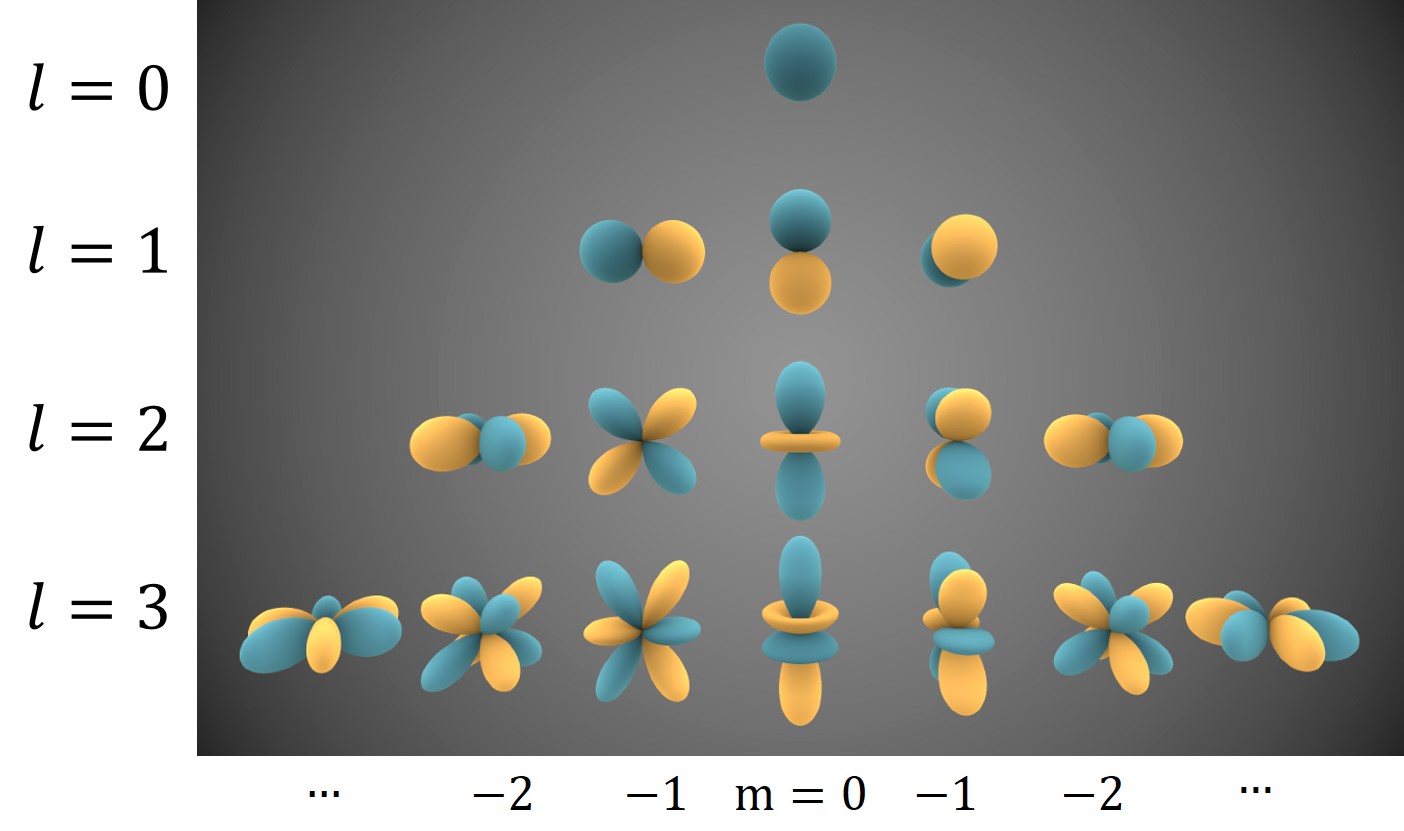
  这个球谐函数表给出了前几阶的SH基函数具体公式，这里不再赘述。这里特别提一点，SH基函数具备一个的良好性质：正交完备性，不同的基函数之间相互正交，即有：

  而上式如果$i=j$，那么：

  我们知道，三维的方向向量可以转换成用球面坐标系下的$(\theta,\phi)$来表示。因此任何一个关于三维方向$\omega$的函数$f(\omega)$都可以转换成球面函数，该函数在SH基函数$B_i(\omega)$下的权重计算（即投影）公式为：

  投影之后，再用$c_i$权重带入公式$(9)$可以对原始函数$f(\omega)$进行复原，这个过程我们称之为重建。当然，由于级数有无穷多个，我们通常也就用前几阶的SH基函数进行重建，相应带来的影响就是去掉了后面SH基函数蕴含的高频信息（频率截断，即低通滤波），结果只是对原函数的近似。

  我们把目光放回到渲染方程上面：

  其中$\rho$是BRDF项，$V(i)$为可见性项。这个方程跟前面提到的形式不太一样，但本质不变，这里懒得改过来了。我们可以把积分里面的函数分成三类，分别是lighting项$L(i)$、visibility项$V(i)$和BRDF项$\rho(i,o)max(0,n\cdot i)$。如果我们直接暴力打表，为场景中的每个点，预计算存储上面的lighting项、visibility项和BRDF项，纹理分辨率为$64\times 64$，那么每个点的存储开销为$6\times 64\times 64$（之所以是$6$，是因为lighting项和BRDF项各占三个数，visibility项占一个数）。而且这仅仅是关于积分内的函数预存储，接下来还需要求解半球的积分方程！

  这种暴力存储的方法并不可取，由此有研究者提出了一种非常精妙的方法来求解上述方程——Precomputed Radiance Transfer，简称PRT。PRT方法不仅极大减小了存储的开销，而且还巧妙地把半球的积分方程转化成SH基函数空间下的向量点乘（或者向量矩阵乘）操作，非常快速地实现了全局光照的效果！

  PRT算法把前面公式$(12)$积分里面的函数分成两部分：$L_(i)$为lighting项，剩余的$V(i)\rho(i,o)max(0,n\cdot i)$被记为light transport项。先假定视角$o$固定不变，那么这两个项都是关于入射方向$i$的球面函数，都可以对其进行SH级数展开。

  对lighting项的展开我们记为：

  对light transport项的展开我们记为：

  其中的$\omega_i$就是我们上面提到的入射方向$i$，$l_p$和$t_q$分别是相应的投影权重。将公式$(13)$和公式$(14)$带入渲染方程$(12)$，我们有如下的近似关系：

  根据我们前面提到的正交完备性，可知当$p\neq q$时，积分结果为$0$；当$p=q$时，积分结果为$1$。故而公式$(15)$可以继续化简为:

  最终的公式直接把积分去掉了！这就是PRT算法的神奇之处。公式$(16)$告诉我们，如果我们能够计算出$l_i$和$t_i$，那么渲染方程结果就是这两个乘积的和。而这所谓的乘积的和实际上就是两个向量的点乘，向量维数取决于采用了多少个SH基函数，如果采用前三阶SH基函数，那么一共有$9$个，$l$和$t$分别是一个$9$维向量，每一个维度是一个rgb向量，即$9\times 3$个数。注意，每个rgb通道各自采用上述的公式$(16)$独立计算（即$l_i\cdot t_i$并非两个rgb向量点乘，特别注意！！！），因此计算结果也是一个rgb向量。

  总而言之，PRT算法的关键之处在于$l$和$t$的计算。$l$是lighting项的SH基函数投影，套用前面的投影公式$(11)$则有：

  其中的积分区域$S$为球面所有方向。而$t$的计算类似，只是将light transport项代入投影公式即可：

  这里的计算有一个比较棘手的地方。前面我们假设$\omega_o$固定不变，但如果$\omega_o$变了呢？对于diffuse的BRDF，其本身与$\omega_o$无关，因此$\omega_o$无论如何变化，在预计算阶段我们都可以直接忽略。但如果是glossy材质，$f_r$是会随着观察视角$\omega_o$的变化而变化的！为此，对于glossy材质的BRDF，我们写成如下形式：

  即对于glossy材质，我们需要增加一个变量$\omega_o$进行打表。遍历$\omega_o$的离散取值，为每一个不同的$\omega_o$生成一个light transport向量$t(\omega_o)$，因此glossy材质的$t$是一个矩阵，矩阵规模为$m\times n$，其中$m$是SH基函数个数，$n$是$\omega_o$离散化个数。对于glossy材质，计算最终的光照辐射率时是$l$向量和$t$矩阵的矩阵向量乘。

  总而言之，对于diffuse材质，我们用公式$(17)$和公式$(18)$预计算$l$向量和$t$向量；对于glossy材质，我们用公式$(17)$和公式$(19)$计算$l$向量和$t$矩阵。最后用公式$(16)$计算光照辐射率。注意预计算阶段，$l$向量只需计算一次，而$t$则需要遍历场景中的所有点（例如网格顶点），为每个点计算一个$t$，然后作为顶点的属性值一起传输到着色器中。这些积分公式的求解，有很多方法，例如最基本的黎曼和亦或者蒙特卡洛积分。

四、diffuse材质的PRT实现

  这里以diffuse材质为例讲一下PRT的实现。PRT的实现分成两个步骤：预计算阶段和实时渲染阶段。对于diffuse材质，其BRDF为以下的lambertian公式：

  其中，$\rho$为材质表面的反照率（diffuse颜色），这里我们假定其取值为$(1,1,1)$。因此，我们可以对前面的公式$(18)$进行简化，有：

  把公式中的$V(\omega_i)$去掉就是不考虑场景自遮挡的情况。在这里我们只用前三阶SH基函数，那么一共有$9$个基函数，因此$p$取值为$0$到$8$。我们先来看lighting项的投影预计算，lighting项的投影公式为：

  我们用黎曼和来对上述的积分公式进行近似：

  在实现时，我们遍历cubemao的所有像素，每个像素构成一个方向$\omega_i$，套用上面的黎曼和公式计算。球谐函数直接调库，这方便的轮子没必要再自己去造。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
constexpr int SHNum = (SHOrder + 1) * (SHOrder + 1);
std::vector<Eigen::Array3f> SHCoeffiecents(SHNum);
for (int i = 0; i < SHNum; i++)
{
    SHCoeffiecents[i] = Eigen::Array3f(0);
}

float sumWeight = 0;
for (int i = 0; i < 6; i++)
{
    for (int y = 0; y < height; y++)
    {
        for (int x = 0; x < width; x++)
        {
            Eigen::Vector3f dir = cubemapDirs[i * width * height + y * width + x];
            int index = (y * width + x) * channel;
            Eigen::Array3f Le(images[i][index + 0], images[i][index + 1],
                images[i][index + 2]);

            float dwi = CalcArea(x, y, width, height);
            Eigen::Vector3d _dir(Eigen::Vector3d(dir[0], dir[1], dir[2]).normalized());
            for (int l = 0; l <= SHOrder; l++)
            {
                for (int m = -l; m <= l; m++)
                {
                    SHCoeffiecents[sh::GetIndex(l, m)] += Le * (float)(sh::EvalSH(l, m, _dir)) * dwi;
                }
            }

        }
    }
}

  对于light transport的预计算，也是对前面的公式$(21)$类似的计算过程。只不过需要为每个顶点都计算一个$t$向量，然后存储到文件中。可见性函数我们用光线与场景的求交来实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
std::unique_ptr<std::vector<double>> ProjectFunction(
    int order, const SphericalFunction& func, int sample_count) 
{
  CHECK(order >= 0, "Order must be at least zero.");
  CHECK(sample_count > 0, "Sample count must be at least one.");

  // This is the approach demonstrated in [1] and is useful for arbitrary
  // functions on the sphere that are represented analytically.
  const int sample_side = static_cast<int>(floor(sqrt(sample_count)));
  std::unique_ptr<std::vector<double>> coeffs(new std::vector<double>());
  coeffs->assign(GetCoefficientCount(order), 0.0);

  // generate sample_side^2 uniformly and stratified samples over the sphere
  std::random_device rd;
  std::mt19937 gen(rd());
  std::uniform_real_distribution<> rng(0.0, 1.0);
  for (int t = 0; t < sample_side; t++) {
    for (int p = 0; p < sample_side; p++) {
      double alpha = (t + rng(gen)) / sample_side;
      double beta = (p + rng(gen)) / sample_side;
      // See http://www.bogotobogo.com/Algorithms/uniform_distribution_sphere.php
      double phi = 2.0 * M_PI * beta;
      double theta = acos(2.0 * alpha - 1.0);

      // evaluate the analytic function for the current spherical coords
      double func_value = func(phi, theta);

      // evaluate the SH basis functions up to band O, scale them by the
      // function's value and accumulate them over all generated samples
      for (int l = 0; l <= order; l++) {
        for (int m = -l; m <= l; m++) {
          double sh = EvalSH(l, m, phi, theta);
          (*coeffs)[GetIndex(l, m)] += func_value * sh;
        }
      }
    }
 }
 
m_TransportSHCoeffs.resize(SHCoeffLength, mesh->getVertexCount());
for (int i = 0; i < mesh->getVertexCount(); i++)
{
    const Point3f& v = mesh->getVertexPositions().col(i);
    const Normal3f& n = mesh->getVertexNormals().col(i);
    auto shFunc = [&](double phi, double theta) -> double
    {
        Eigen::Array3d d = sh::ToVector(phi, theta);
        const Vector3f wi = Vector3f(d.x(), d.y(), d.z());
        float cos_theta = wi.dot(n);
		if (wi.dot(n) > 0.0f)
		{
			if (!scene->rayIntersect(Ray3f(v, wi)))
			{
				return wi.dot(n) / M_PI;
			}
		}
        return 0;
    };

    auto shCoeff = sh::ProjectFunction(SHOrder, shFunc, m_SampleCount);
    for (int j = 0; j < shCoeff->size(); j++)
    {
        m_TransportSHCoeffs.col(i).coeffRef(j) = (*shCoeff)[j];
    }
}

  而如果要考虑多次弹射，那么可以通过迭代的方式计算$t$。在前一次迭代的基础上，从每个顶点发射一条射线，如果射线打中了另一个点，那么通过线性插值得到该点的前一次$t$，再乘以余弦项，最后累加。详情见下面代码（想偷懒了）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
auto tmp = m_TransportSHCoeffs;
auto interrefl = [&](const Point3f& v, const Normal3f& n,
    int order, int sample_count) -> std::unique_ptr<std::vector<double>>
{
    // This is the approach demonstrated in [1] and is useful for arbitrary
    // functions on the sphere that are represented analytically.
    const int sample_side = static_cast<int>(floor(sqrt(sample_count)));
    std::unique_ptr<std::vector<double>> coeffs(new std::vector<double>());
    coeffs->assign(sh::GetCoefficientCount(order), 0.0);

    // generate sample_side^2 uniformly and stratified samples over the sphere
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_real_distribution<> rng(0.0, 1.0);
    for (int t = 0; t < sample_side; t++)
    {
        for (int p = 0; p < sample_side; p++)
        {
            double alpha = (t + rng(gen)) / sample_side;
            double beta = (p + rng(gen)) / sample_side;
            double phi = 2.0 * M_PI * beta;
            double theta = acos(2.0 * alpha - 1.0);

            Eigen::Array3d d = sh::ToVector(phi, theta);
            const Vector3f wi = Vector3f(d.x(), d.y(), d.z());

            Intersection its;
            bool intersected = scene->rayIntersect(Ray3f(v, wi), its);
            float V = (1 - intersected ? 0 : 1) * wi.dot(n);//(1-v)*cos_theta

            if (V > 0.f)
            {
                const Vector3f& bary = its.bary;
                auto vertIndex = its.tri_index;
                for (int l = 0; l <= order; l++)
                {
                    for (int m = -l; m <= l; m++)
                    {
                        //double sh = EvalSH(l, m, phi, theta);
                        int index = sh::GetIndex(l, m);
                        float lastSH =
                            bary.x() * tmp.col(vertIndex.x()).coeff(index) +
                            bary.y() * tmp.col(vertIndex.y()).coeff(index) +
                            bary.z() * tmp.col(vertIndex.z()).coeff(index);
                        (*coeffs)[index] += lastSH * V;
                    }
                }
            }
        }
    }

    // scale by the probability of a particular sample, which is
    // 4pi/sample_side^2. 4pi for the surface area of a unit sphere, and
    // 1/sample_side^2 for the number of samples drawn uniformly.
    double weight = 4.0 * M_PI / (sample_side * sample_side);
    for (unsigned int i = 0; i < coeffs->size(); i++)
    {
        (*coeffs)[i] *= weight;
    }

    return coeffs;
};

for (int b = 1; b <= m_Bounce; ++b)
{
    for (int i = 0; i < mesh->getVertexCount(); i++)
    {
        const Point3f& v = mesh->getVertexPositions().col(i);
        const Normal3f& n = mesh->getVertexNormals().col(i);
        auto inteCoeff = interrefl(v, n, SHOrder, m_SampleCount);
        for (int j = 0; j < inteCoeff->size(); j++)
        {
            m_TransportSHCoeffs.col(i).coeffRef(j) += ((*inteCoeff)[j] / M_PI);
        }
    }
    tmp = m_TransportSHCoeffs;
}

  得到了$l$和$t$，在渲染时我们通过存储的文件将这些数据加载进来，然后传到着色器中。Vertex着色器代码如下（重点关注L和LT），这里实现的是Per-Vertex shading。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
attribute vec3 aVertexPosition;
attribute vec3 aNormalPosition;
attribute vec2 aTextureCoord;
attribute mat3 aPrecomputeLT;

uniform mat4 uModelMatrix;
uniform mat4 uViewMatrix;
uniform mat4 uProjectionMatrix;

uniform mat3 uPrecomputedL[3];

varying highp vec2 vTextureCoord;
varying highp vec3 vFragPos;
varying highp vec3 vNormal;
varying highp vec3 vRadiance;

float dot(mat3 L, mat3 LT)
{
    float ret = 0.0;
    ret = L[0][0] * LT[0][0] + L[0][1] * LT[0][1] + L[0][2] * LT[0][2]
        + L[1][0] * LT[1][0] + L[1][1] * LT[1][1] + L[1][2] * LT[1][2]
        + L[2][0] * LT[2][0] + L[2][1] * LT[2][1] + L[2][2] * LT[2][2];
    return ret;
}

void main(void) {

  vFragPos = (uModelMatrix * vec4(aVertexPosition, 1.0)).xyz;
  vNormal = (uModelMatrix * vec4(aNormalPosition, 0.0)).xyz;

  gl_Position = uProjectionMatrix * uViewMatrix * uModelMatrix *
                vec4(aVertexPosition, 1.0);

  vTextureCoord = aTextureCoord;

  vRadiance = vec3(
      dot(uPrecomputedL[0], aPrecomputeLT),
      dot(uPrecomputedL[1], aPrecomputeLT),
      dot(uPrecomputedL[2], aPrecomputeLT));

}

  Fragment着色器代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#ifdef GL_ES
precision mediump float;
#endif

uniform sampler2D uSampler;

varying highp vec2 vTextureCoord;
varying highp vec3 vFragPos;
varying highp vec3 vNormal;
varying highp vec3 vRadiance;

void main(void) 
{
  gl_FragColor = vec4(vRadiance * 2.0, 1.0);
}

  实现的效果比较见下图。

Reference

$[1]$ Sloan P P, Kautz J, Snyder J. Precomputed radiance transfer for real-time rendering in dynamic, low-frequency lighting environments[C]//Proceedings of the 29th annual conference on Computer graphics and interactive techniques. 2002: 527-536.

$[2]$ GAMES202: 高质量实时渲染

 上一页

Computer Graphics Real-time Rendering

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 ， 总访问量为 次 。
载入天数...载入时分秒...