Physically Based Rendering：体积散射

WC Yang

2020-04-19

Computer Graphics / Ray Tracer

在不考虑空气介质的散射效应时，我们假定光线在真空中传播，故光线的辐射率在传播过程不会发生变化。但真实地球世界却并非真空，大气散射、烟雾散射等丁达尔效应现象对渲染结果至关重要，这类光学效果涉及到散射介质，光线在此类介质中被吸收、散射，最终到达人眼的辐射率与未考虑介质散射的有非常明显的不同。

以下的内容大部分整理自pbrt第三版的第十章——VOLUME SCATTERING。

一、体积散射效应

光线在参与介质（participating media）中传播的辐射率分布主要受以下三个方面的影响：

吸收（Absorption）：光线与介质中的粒子碰撞，直接将光能转换成其它形式的能量，例如热能，因此光线的辐射率被衰减了；
发光（Emission）：介质中的发光粒子产生的辐射率附加到光线上，因此光线的辐射率被增强了；
散射（Scattering）：光线与介质中的粒子碰撞，导致光线的传播方向发生了变化，对于给定的传播方向，既有该方向上的光线向外散射到其他方向（外散射），又有其他方向的光线被散射并融入到该方向上（内散射）。

这些体积散射效应按照介质的类别又可以分为均匀（homogeneous）散射和非均匀（inhomogeneous）散射。均匀散射指参与介质在其分布的空间中是均匀分布的（可以看成参与介质的粒子是均匀散落在空间中），此类介质的散射比较简单；非均匀散射则是指光线在非均匀分布的参与介质中传播，例如地球的大气层，从海平面逐渐升高空气的密度逐渐稀薄。

1、吸收

阳光照射到空气中的烟雾，也会在地面上投射出一个阴影轮廓，这是因为光线经过烟雾介质时一部分的辐射率被吸收了，导致到达地面上的辐射率低了不少，从而形成阴影。烟雾越浓越厚，则阴影越明显。介质的吸收性质通常用介质的吸收截面$\sigma_a$（absorption cross section）来表示，它描述了光透过介质中的单位距离时被吸收的分量，因此这是一个概率密度函数，单位为距离的倒数$m^{-1}$。吸收截面通常与空间中的位置$p$和介质的光谱有关，但在某些特殊情况下也与方向$\omega$有关。值得注意的是，虽然$\sigma_a$是概率密度，但它的取值并没有被限制于$0$到$1$之间，因此需要进一步取自然底数$e$的指数转换成吸收概率密度值（后面会看到）。

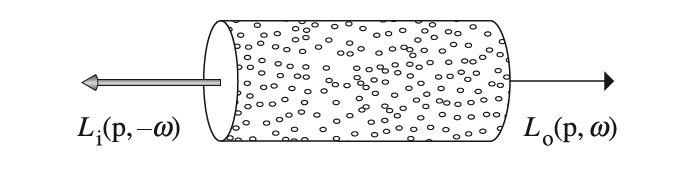
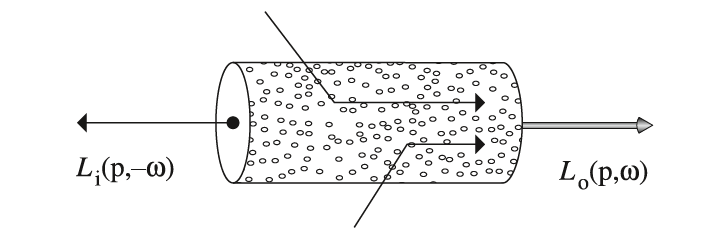
下图展示了光线在介质中经过的一段极短的距离（以$p$点为中心）被吸收的情况，设该极短距离为$dt$。光线从左边入射进来，其辐射率为$L_i(p,-\omega)$，与介质中的粒子碰撞被吸收之后的出射辐射率记为$L_o(p,\omega)$。现给定吸收截面$\sigma_a$，则被吸收的微分辐射率为：

$L_o(p,\omega)-L_i(p,-\omega)=dL_o(p,\omega)=-\sigma_a(p,\omega)L_i(p,-\omega)dt \tag {1.1}$

上式给出了光线被吸收的辐射率值，它表明被吸收的微分辐射率$dL_o$是其初始辐射率$L_i$的线性函数。

因此，给定光线的起始点$p$和入射方向$\omega$，光线在介质中穿过$d$距离时，经过吸收衰减之后，剩余的辐射率占据原来的辐射率比值为如下的指数上的积分形式：

$e^{-\int_0^d \sigma_a(p+\omega t,\omega)dt} \tag {1.2}$

即对$[0,d]$上的吸收截面$\sigma_a$进行积分，得到总的吸收率，再取负就得到剩余的能量比例。

2、发光

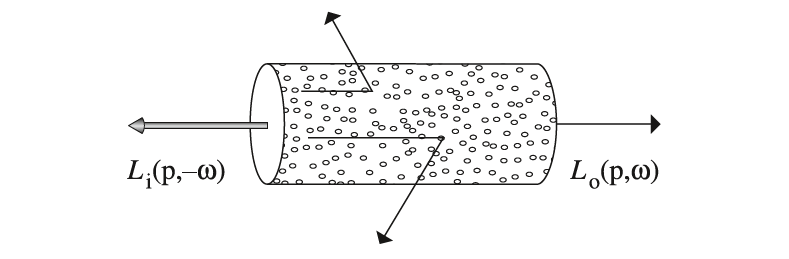
一方面光线透过介质被吸收导致衰减，但另一方面，介质中的发光粒子会产生光能，汇入到传播的光线当中。介质中的发光粒子的产生原因有很多，例如化学反应等。下图依旧以一个微分距离$dt$为例，记介质的发光辐射率为$L_e(p,\omega)$，它是关于位置$p$和方向$\omega$的函数，描述了单位距离上的发光辐射率值。

因此，经过上图的微分距离$dt$，新增的微分辐射率为：

$dL_o(p,\omega)=L_e(p,\omega) dt \tag {1.3}$

在这里，我们假定发光辐射率$L_e(p,\omega)$与入射辐射率$L_i$无关。

3、外散射

对于给定的光线传播方向$\omega$，根据散射方向的不同，可以分成内散射和外散射。对于给定的光线传播方向，因为与介质粒子碰撞导致光线的方向被弹射至其它方向，减弱了原本光线辐射率，这就是外散射；而又因为周围粒子的外散射导致其他方向的光线被弹射到当前的光线传播方向，增加了原本光线辐射率，这就是内散射。内散射源于外散射，两者不是排斥关系。这里先来看外散射效应。

每单位距离的外散射的概率密度用散射系数$\sigma_s$。与吸收类似，外散射导致的减少的微分辐射率为：

$dL_o(p,\omega)=-\sigma_s(p,\omega)L_i(p,-\omega)dt$

通常，对于辐射率的衰减，我们把吸收和外散射两个因素综合起来一起计算，因此总的衰减比例为吸收截面加上散射系数：$\sigma_a+\sigma_s$。光线的吸收和外散射我们统一称为衰减（attenuation）或消光（extinction），用衰减系数$\sigma_t$记为两者之和：

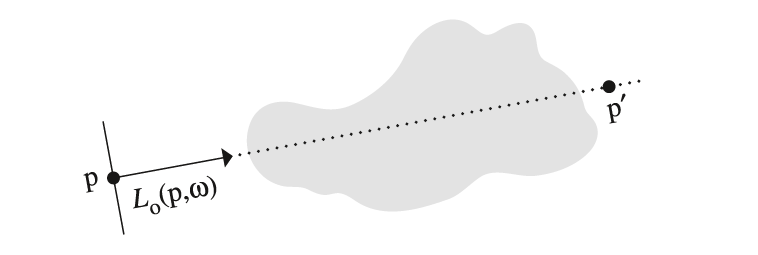
$\sigma_t(p,\omega)=\sigma_a(p,\omega)+\sigma_s(p,\omega) \tag {1.4}$

给定了介质的衰减系数$\sigma_t$，辐射率的衰减速率为$\frac{dL_o(p,\omega)}{dt}=-\sigma_t(p,\omega) L_i(p,\omega)$。给定要通过的路径的两个端点$p$和$p’$（如下图所示），以下的积分公式计算光线通过这条路径时，除去被吸收和被外散射的，剩余的辐射率占比，我们称之为光束透射率（beam transmittance）：

$T_r(p\to p')=e^{-\int_0^d\sigma_t(p+t\omega,\omega)dt} \tag {1.5}$

其中$d=||p-p’||$是$p$和$p’$之间的直线距离，$\omega$是$p\to p’$的单位方向向量。

公式$(1.5)$计算得到的光束透射率取值介于$0$到$1$之间，本质上是个百分比。因此，经过衰减之后到达$p’$点的辐射率就是起始点$p$的辐射率再乘上光束透射率：

$T_r(p\to p')L_o(p,\omega)$

来观察观察一下光束透射率即公式$(1.5)$的一些性质。当介质为真空时，即$\sigma_t=0$，则$T_r=1$；当$p=p’$时，$T_r=1$。符合物理常识。此外，若衰减系数$\sigma_t$是关于方向对称的，即$\sigma_t(\omega)=\sigma_t(-\omega)$，或者$\sigma_t$仅仅是关于位置的函数，则介质中两点之间的透射率亦符合如下的对称性：

$T_r(p\to p')=T_r(p'\to p)$

关于光束透射率的另一个重要的属性就是，对于任意的介质，有如下的性质：

$T_r(p\to p'')=T_r(p\to p')T_r(p'\to p'')$

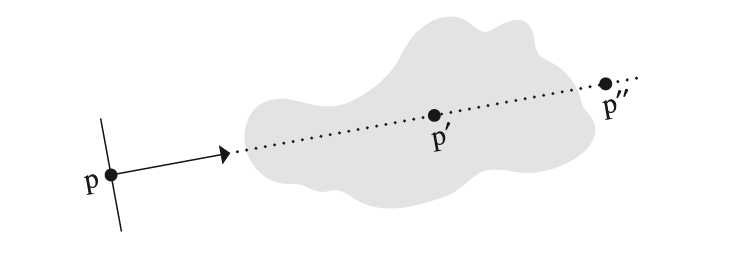
其中，$p’$是介于$p$和$p’’$之间的任意一点，如下图所示。这个性质非常有用，把原本$T_r(p\to p’’)$的求解拆分成两段独立的$T_r(p\to p’)$和$T_r(p’\to p’’)$的求解，最后再通过相乘得到$T_r(p\to p’’)$。

公式$(1.5)$中的指数取反就是两点之间的光学厚度（optical thickness），用符号$\tau$表示：

$\tau(p\to p')=\int_{o}^d \sigma_t(p+t\omega,-\omega)dt \tag {1.6}$

求解公式$(1.5)$的关键就是求解光学厚度$(1.6)$。对于均匀介质，衰减系数$\sigma_t$是一个常量值，因此可以可以直接计算出光学厚度$\tau=\sigma_t d$，从而得出了Beer定律的光束透射率公式：

$T_r(p\to p')=e^{-\sigma_t d} \tag {1.7}$

这里有两个非常重要的与衰减系数相关的概念。一个是参与介质的反照率（albedo），其公式为$\rho=\frac{\sigma_s}{\sigma_t}$，取值为$[0,1]$，它给出了散射比例；另一个是平均自由路径（mean free path），其公式为$1/\sigma_t$，它给出了一束光线在介质中传播过程中与介质粒子碰撞时走过的平均路径。

4、内散射

与外散射相反，内散射是其他方向的光线被弹射到当前的光线传播方向，增加了当前的光照辐射率值。对于内散射，这里做了一个假设，即介质粒子之间的间隔是粒子半径的数倍（即互不接触），因此在描述散射性质时可以忽略粒子之间的交互作用。基于该假设，给定空间中的一点和光线传播方向$\omega$以及另外一个不同的方向$\omega’$，相位函数（phase function）$p(\omega,\omega’)$描述了从$\omega’$方向上的光线被散射到$\omega$方向的概率密度值，类似于BSDF函数。因此相位函数有如下的归一化约束：

$\int_{S^2}p(\omega,\omega')d\omega' = 1$

即对整个球体方向的积分求和值应该为$1$。通过内散射和发光增加的微分辐射率为：

$dL_o(p,\omega)=L_s(p,\omega) dt$

而$L_s(p,\omega)$综合了发光与内散射效应：

$L_s(p,\omega)=L_e(p,\omega)+\sigma_s(p,\omega)\int_{S^2}p(p,\omega_i,\omega) L_i(p,\omega_i)d\omega{i} \tag {1.8}$

二、相位函数

BSDF模型对于给定的入射方向和出射方向，计算出射辐射率占入射辐照度的比值。而在体积散射中，相位函数也是一个类似的模型。在图形学中用到的相位函数中，有些是通过拟合得到的参数化模型，有些是根据介质形状和材质的散射辐射率分布推导出的解析模型。对于大部分的自然介质，其相位函数是关于$\theta$的一维函数，入射方向$\theta$是$\omega_i$和出射方向$\omega_o$的夹角，这些相位函数通常记为$p(cos\theta)$。此类相位函数对应的参与介质是各向同性的，具有关于入射方向的局部旋转不变性。此外，因为$cos(-\theta)=cos(\theta)$，故该各向同性介质的相位函数具有可逆性，即$\omega_i$和$\omega_o$交换，但相位函数取值不变。对于各向异性的介质，其相位函数通常是关于$\omega_i$和$\omega_o$的四维函数，比较复杂。

这里需要注意的一点就是，相位函数本身亦可以是各向同性或者各向同性的，因此各向同性的介质可以有一个各向异性的相位函数。一个各向同性的相位函数描述的是向所有方向均等散射的情况，因此与$\omega$和$\omega’$这两个方向无关，各向同性的相位函数只有如下面的一个：

$p(\omega_o,\omega_i)=\frac{1}{4\pi}$

$\omega_o$是原本的光线传播方向，$\omega_i$是从其他方向弹射过来的入射方向。创建一个PhaseFunction的接口类如下，其中p(const Vector3f &wo, const Vector3f &wi)就是相位函数的接口，它的输入参数为$\omega_i$和$\omega_o$：

class PhaseFunction {
  public:
    // PhaseFunction Interface
    virtual ~PhaseFunction();
    virtual Float p(const Vector3f &wo, const Vector3f &wi) const = 0;
    virtual Float Sample_p(const Vector3f &wo, Vector3f *wi,
                           const Point2f &u) const = 0;
};

在这里，$\omega_i$和$\omega_o$的方向沿用BSDF的惯例，起始点为$p$，如下图所示。

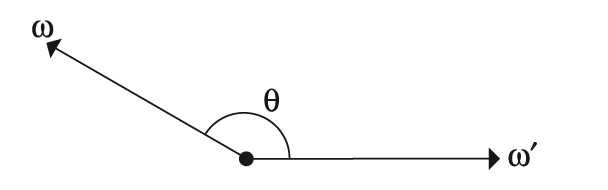
Henyey和Greenstein提出一个现今广泛使用的相位函数，该相位函数的输入参数除了$cos\theta$之外，还有非对称参数$g$。但应用到某个参与介质上时，非对称参数$g$就固定了：

$p_{HG}(cos\theta)=\frac{1}{4\pi}\frac{1-g^2}{(1+g^2+2g(cos\theta))^{3/2}} \tag {2.1}$

非对称参数$g$的取值范围为$[-1,1]$，$g$的不同取值则对应的相位函数分布亦不相同。下图分别展示了$g=-0.35$（实线）和$g=0.67$（虚线）时的Henyey-Greenstein相位函数分布。$g$取$[-1,0]$时光线大部分都从后半球方向散射进来，称之为后向散射（back-scattering）；$g$取$[0,1]$时光线大部分都从前半球方向散射进来，称之为前向散射（forward-scattering）。$g$的绝对值越大，则越偏向于$\omega$（对于前向散射）或者$-\omega$（对于后想散射）方向。

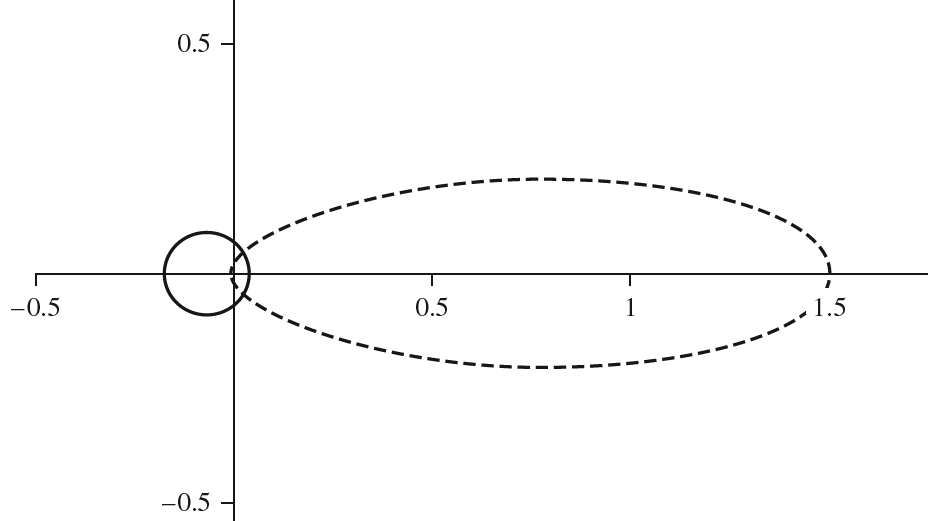
前向散射和后向散射产生的视觉效果差别非常大，下图给出了两者的渲染结果。左边的是后向散射的结果，因此可以模型后面的光线透过模型，抵达人眼，产生透射效果；右边的是前向散射的结果，模型倾向于反射其前方的光线，产生反射效果。

根据公式$(2.1)$，可以实现Henyey-Greenstein相位函数如下：

inline Float PhaseHG(Float cosTheta, Float g) {
    Float denom = 1 + g * g + 2 * g * cosTheta;
    return Inv4Pi * (1 - g * g) / (denom * std::sqrt(denom));
}

class HenyeyGreenstein : public PhaseFunction {
  public:
    // HenyeyGreenstein Public Methods
    HenyeyGreenstein(Float g) : g(g) {}
    Float p(const Vector3f &wo, const Vector3f &wi) const;
    Float Sample_p(const Vector3f &wo, Vector3f *wi,
                   const Point2f &sample) const;
  private:
    const Float g;
};

Float HenyeyGreenstein::p(const Vector3f &wo, const Vector3f &wi) const {
    ProfilePhase _(Prof::PhaseFuncEvaluation);
    return PhaseHG(Dot(wo, wi), g);
}

Henyey-Greenstein模型中的非对称参数$g$实际上有明确的数学意义，是相位函数$p$分布下的$cos\theta$值的数学期望（或者说平均值），这里相位函数是概率密度函数，即：

$g=\int_{S^2}p(-\omega,\omega')(\omega \cdot \omega')d\omega'=2\pi \int_0^\pi p(-cos\theta)cos\theta sin\theta d\theta$

对于各向同性的相位函数（即前面的$\frac{1}{4\pi}$），上面计算得到$g=0$，符合预期结果。更复杂的相位函数可以通过一些简单的相位函数加权叠加得到：

$p(\omega,\omega')=\sum_{i=1}^n \omega_i p_i(\omega\to \omega') \tag {2.2}$

其中，权重的总和$\sum_{i=1}^n\omega_i$应该等于$1$，确保相位函数的归一化性质。pbrt并没有实现该类相位函数。

三、参与介质

自然界中的散射介质形态各异，有些没有明显的物体边界（例如烟雾、大气层），而有些却有明显的物体边界（例如人体的皮肤）。尽管某些参与介质没有明确的边界，但通常拥有一个包围盒或者类似于包围盒的复杂几何体来表示介质涉及的最大范围，然后在渲染的时候并不渲染这个包围几何体即可。关于这方便的设定不再赘述。

有了边界，现在的问题就是如何描述边界之内的参与介质的分布情况。对于均匀的散射介质，介质粒子的密度为常量，根本不需要用额外的数据结构去存储参与介质的分布数据。而对于非均匀的散射介质，则要麻烦一些。这里首先创建一个Medium接口类，函数Tr是计算光束透射率的接口：

class Medium {
  public:
    // Medium Interface
    virtual ~Medium() {}
    virtual Spectrum Tr(const Ray &ray, Sampler &sampler) const = 0;
    virtual Spectrum Sample(const Ray &ray, Sampler &sampler,
                            MemoryArena &arena,
                            MediumInteraction *mi) const = 0;
};

1、均匀介质表示

均匀介质（Homogeneous medium）是一类最简单的参与介质，也是一种最高效的介质模型，在图形领域亦有诸多应用。均匀介质其密度为某个常量值，因此其吸收截面$\sigma_a$和散射系数$\sigma_s$在整个介质区域内亦为常量。因此可以直接省去计算光学深度的积分公式，直接套用前面提到的Beer透射定律公式$(1.7)$，即：

$T_r(p\to p')=e^{-\sigma_t d}$

Spectrum HomogeneousMedium::Tr(const Ray &ray, Sampler &sampler) const {
    ProfilePhase _(Prof::MediumTr);
    return Exp(-sigma_t * std::min(ray.tMax * ray.d.Length(), MaxFloat));
}

2、非均匀介质表示

对于非均匀的散射介质，其密度随着空间位置的变化而变化（例如空气密度从海平面到高空逐渐稀薄），一般很难找到某种显式的数学解析式描述介质密度的空间分布情况。为此，一种表示非均匀介质的方法类似于离散采样，构建一个三维的均匀网格，在每个网格点上记录介质的密度值。则对于空间中的任意一点的密度值，可以通过其所在格子的八个顶点的密度值线性插值得到（三线性插值，当然也可以用B样条插值）。

此种表示方法在连续介质例如流体的物理模拟中使用非常多，思想比较简单，关键是非均匀介质的密度数据的获取，密度数据的获取一般亦是通过物理模拟得到，这里只负责利用这些数据渲染。对于非均匀介质，因其密度分布没有显式的数学公式表达，因此亦只能通过数值方法求解下面的光束透射率：

$T_r(p\to p')=e^{-\int_0^d\sigma_t(p+t\omega,\omega)dt}$

求解的关键是$\int_0^d \sigma_t(p+t\omega,\omega)dt$即光学深度的积分，一种常用的方法就是利用梯度法求解该积分公式，还有一些则是基于随机采样的方法求解该积分（例如蒙特卡洛方法）。光束透射率的求解pbrt这里并没有提，暂时先跳过具体的细节。

四、BSSRDF

类似于BSDF模型，BSSRDF（Bidirectional scattering-surface reflectance distribution function，双向散射表面反射分布函数）模型描述了在出射点$p_o$和出射方向上$\omega_o$的出射辐射率占表面上另一个点$p_i$和入射方向$\omega_i$的入射辐照度的比值，通常记为$S(p_o,\omega_o,p_i,\omega_i)$。由此，次表面散射的反射方程是对物体表面和半球方向的多重积分：

$L_o(p_o,\omega_o)=\int_A \int_{H^2(n)} S(p_o,\omega_o,p_i,\omega_i)L_i(p_i,\omega_i)|cos\theta_i|d\omega_i dA \tag {4.1}$

其中$A$是介质的所有表面，这就是体积散射要求解的渲染方程。该方程虽然是物理准确的，但即便对于离线渲染，直接求解亦是不切实际。BSSRDF是一个高维函数，研究者们已经提出了一系列的简化模型来提高渲染效率。BSSRDF的计算与介质内部和外部的折射系数密切相关，因此通常需要内部和外部的相对折射指数作为其计算的参数。这里先创建一个BSSRDF接口类：

class BSSRDF {
  public:
    // BSSRDF Public Methods
    BSSRDF(const SurfaceInteraction &po, Float eta) : po(po), eta(eta) {}
    virtual ~BSSRDF() {}
    // BSSRDF Interface
    virtual Spectrum S(const SurfaceInteraction &pi, const Vector3f &wi) = 0;
    virtual Spectrum Sample_S(const Scene &scene, Float u1, const Point2f &u2,
                              MemoryArena &arena, SurfaceInteraction *si,
                              Float *pdf) const = 0;
  protected:
    // BSSRDF Protected Data
    const SurfaceInteraction &po;
    Float eta;
};

其中，S就是BSSRDF函数接口。

1、可分离的BSSRDF

相比于BSDF模型，BSSRDF模型复杂了不少，其中一个关键就是其对介质表面的依赖，很难找到一种通用的BSSRDF模型适用于任意形状的物体表面。这里来看一种简化的BSSRDF模型，它将$S(p_o,\omega_o,p_i,\omega_i)$拆分成如下的三种独立函数的乘积形式：

$S(p_o,\omega_o,p_i,\omega_i)\approx (1-F_r(cos\theta_o))S_p(p_o,p_i)S_{\omega}(\omega_i) \tag {4.2}$

其中，$F_r$和$S_\omega$是关于方向的函数，而$S_p$是关于空间的函数。

Spectrum S(const SurfaceInteraction &pi, const Vector3f &wi) {
    ProfilePhase pp(Prof::BSSRDFEvaluation);
    Float Ft = FrDielectric(CosTheta(po.wo), 1, eta);
    return (1 - Ft) * Sp(pi) * Sw(wi);
}

公式$(4.2)$中的$(1-F_r(cos\theta))$不难理解，$F_r(cos\theta)$给出了菲涅尔反射率，故剩余比例的为透射率，它给出了在$p_o$上向$\omega_o$方向透射的光能辐射率的比例，确保符合能量守恒。而$S_\omega(\omega_i)$描述了在$p_i$上向$\omega_i$入射的分布情况，其在菲涅尔方程的基础上再乘上一个缩放系数：

$S_\omega(\omega_i)=\frac{1-F_r(cos\theta_i)}{c\pi} \tag {4.3}$

上式中的缩放系数$c$是一个归一化因子，它使得：

$\int_{H^2}S_\omega(\omega)cos\theta d\omega=1$

也就是说，$c$的计算公式为：

$\begin{align} c=&\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}\frac{1-F_r(\eta,cos\theta)}{\pi}sin\theta cos\theta d\theta d\phi\\ =&1-2\int_o^{\frac{\pi}{2}}F_r(\eta,cos\theta)sin\theta cos\theta d\theta \end{align} \tag {4.4}$

上面计算$c$的积分实际上只是关于菲涅尔方程的一阶矩（first moment），次表面散射中有多阶矩的$c$的应用，其区别在于上面公式中的$cos\theta$的指数$i$，更通用的$i$阶菲涅尔矩的公式为：

$\overline F_{r,i}(\eta)=\int_0^{\frac{\pi}{2}}F_r(\eta,cos\theta)sin\theta cos^i\theta d\theta \tag {4.5}$

但计算积分还是太麻烦了，因此实现的时候实际上用一个近似拟合上述积分公式的多项式去计算：

Float FresnelMoment1(Float eta) {
    Float eta2 = eta * eta, eta3 = eta2 * eta, eta4 = eta3 * eta,
          eta5 = eta4 * eta;
    if (eta < 1)
        return 0.45966f - 1.73965f * eta + 3.37668f * eta2 - 3.904945 * eta3 +
               2.49277f * eta4 - 0.68441f * eta5;
    else
        return -4.61686f + 11.1136f * eta - 10.4646f * eta2 + 5.11455f * eta3 -
               1.27198f * eta4 + 0.12746f * eta5;
}

用公式$(4.4)$计算出缩放系数$c$，然后再代入公式$(4.3)$计算$S_\omega$：

Spectrum Sw(const Vector3f &w) const {
    Float c = 1 - 2 * FresnelMoment1(1 / eta);
    return (1 - FrDielectric(CosTheta(w), 1, eta)) / (c * Pi);
}

最后就是函数$S_p(p_i,p_o)$的计算。这里再次做了近似简化，注意到$p_i$和$p_o$相距越远，则从$p_i$入射进来的辐射率对$p_o$出射的辐射率贡献越小，因此假定物体形状是一个平面，将$S_p(p_i,p_o)$近似逼近成如下的一维公式：

$S_p(p_i,p_o)\approx S_r(||p_o-p_i||) \tag {4.6}$

$||p_o-p_i||$是该两点之间的直线距离。具体的$S_r(||p_o-p_i||)$公式取决于具体的BSSRDF函数，这里暂不展开。值得注意的是，将$S_p(p_i,p_o)$近似成上面的一维函数蕴含了一个假设，就是散射介质是相对比较均匀的。而且如果介质几何体越复杂（越不是一个平面），则上面的近似误差越大。

2、基于查找表的BSSRDF

正如之前提到的傅里叶基下打表的BSDF模型，BSSRDF模型也可以通过真实实验测量的数据得到，并在渲染时查找这些数据并做相应的插值（线性插值或B样条插值）。在可分离的BSSRDF模型上，我们只需要存储前面提到的$S_r(||p_o-p_i||)$函数，其余两个函数均可以快速计算得到。

乍一看$S_r(||p_o-p_i||)$是一个一维函数，但其实不然。这里有隐性的关联，$S_r(||p_o-p_i||)$与散射材质息息相关，不同的散射介质应该有不同的$S_r$函数。因此，$S_r$还有额外的四个参数：折射指数$\eta$、散射非对称系数$g$、反照率$\rho$和衰减系数$\sigma_t$。即$S_r(\eta,g,\rho,\sigma_t,r)$，其中$r=||p_o-p_i||$，这是个五维函数，直接离散打表不太可能，因为这需要非常大的存储空间。因此需要适当地降维。

首先$\sigma_t$和$r$可以合并成一个参数，$r_{optical}=\sigma_t r$，称之为光学半径，这样所有的参数都是无量纲：

$S_r(\eta,g,\rho,\sigma_t,r)=\sigma_t^2S_r(\eta,g,\rho,1,r_{optical})$

转换成右边形式的还要乘上$\sigma_t^2$补偿参数转变的损失。除此之外，令$\eta$和$g$取值固定，最后$S_r$就是关于$\rho$和$r$的二维函数，因此打表的BSSRDF只需存储反照率$\rho$和光学半径$r$的离散值，分别对应下面的rhoSamples和radiusSamples：

struct BSSRDFTable {
    // BSSRDFTable Public Data
    const int nRhoSamples, nRadiusSamples;
    std::unique_ptr<Float[]> rhoSamples, radiusSamples;
    std::unique_ptr<Float[]> profile;
    std::unique_ptr<Float[]> rhoEff;
    std::unique_ptr<Float[]> profileCDF;

    // BSSRDFTable Public Methods
    BSSRDFTable(int nRhoSamples, int nRadiusSamples);
    inline Float EvalProfile(int rhoIndex, int radiusIndex) const {
        return profile[rhoIndex * nRadiusSamples + radiusIndex];
    }
};

有了BSSRDFTable，则在计算$S_r$时就根据$r_{optical}$和$\rho$做适当的B样条插值即可，因为返回的是一个光谱值，因此对光谱的每一个通道都进行插值和计算的过程：

Spectrum TabulatedBSSRDF::Sr(Float r) const {
    Spectrum Sr(0.f);
    for (int ch = 0; ch < Spectrum::nSamples; ++ch) {
        // Convert $r$ into unitless optical radius $r_{\roman{optical}}$
        Float rOptical = r * sigma_t[ch];

        // Compute spline weights to interpolate BSSRDF on channel _ch_
        int rhoOffset, radiusOffset;
        Float rhoWeights[4], radiusWeights[4];
        if (!CatmullRomWeights(table.nRhoSamples, table.rhoSamples.get(),
                               rho[ch], &rhoOffset, rhoWeights) ||
            !CatmullRomWeights(table.nRadiusSamples, table.radiusSamples.get(),
                               rOptical, &radiusOffset, radiusWeights))
            continue;

        // Set BSSRDF value _Sr[ch]_ using tensor spline interpolation
        Float sr = 0;
        for (int i = 0; i < 4; ++i) {
            for (int j = 0; j < 4; ++j) {
                Float weight = rhoWeights[i] * radiusWeights[j];
                if (weight != 0)
                    sr += weight *
                          table.EvalProfile(rhoOffset + i, radiusOffset + j);
            }
        }

        // Cancel marginal PDF factor from tabulated BSSRDF profile
        if (rOptical != 0) sr /= 2 * Pi * rOptical;
        Sr[ch] = sr;
    }
    // Transform BSSRDF value into world space units
    Sr *= sigma_t * sigma_t;
    return Sr.Clamp();
}

这里提到了有效反照率（effective albedo），不是很明白为什么要这样做，先放着。

3、次表面散射材质

pbrt实现了两类次表面散射材质，分别是SubsurfaceMaterial和KdSubsurfaceMaterial。SubsurfaceMaterial材质是一个有明确表面的材质，例如完美镜面透射或者gloosy镜面透射等。因此该材质除了BSSRDF模型，还有BSDF模型。关于BSDF模型，这里不再具体赘述。下面的scale、table、eta、sigma_a和sigma_s用于BSSRDF模型的计算：

class SubsurfaceMaterial : public Material {
  public:
    // SubsurfaceMaterial Public Methods
   	...

  private:
    // SubsurfaceMaterial Private Data
    const Float scale;
    std::shared_ptr<Texture<Spectrum>> Kr, Kt, sigma_a, sigma_s;
    std::shared_ptr<Texture<Float>> uRoughness, vRoughness;
    std::shared_ptr<Texture<Float>> bumpMap;
    const Float eta;
    const bool remapRoughness;
    BSSRDFTable table;
};

scale用于对吸收截面和散射系数的缩放（因此要求单位为$m^{-1}$）。在材质类的ComputeScatteringFunctions函数中初始化相关的bssrdf函数：

void SubsurfaceMaterial::ComputeScatteringFunctions(
    SurfaceInteraction *si, MemoryArena &arena, TransportMode mode,
    bool allowMultipleLobes) const {
    // Perform bump mapping with _bumpMap_, if present
    if (bumpMap) Bump(bumpMap, si);

    // Initialize BSDF for SubsurfaceMaterial
    ...
    
    Spectrum sig_a = scale * sigma_a->Evaluate(*si).Clamp();
    Spectrum sig_s = scale * sigma_s->Evaluate(*si).Clamp();
    si->bssrdf = ARENA_ALLOC(arena, TabulatedBSSRDF)(*si, this, mode, eta,
                                                     sig_a, sig_s, table);
}

直接设置吸收截面和散射系数并不是非常直观，因此pbrt创建了KdSubsurfaceMaterial材质，方便直接根据漫反射反射率和自由平均路径$1/\sigma_t$间接设置吸收截面和散射系数，使得这两个参数的设置变得直观起来。从反射率和自由平均路径计算吸收截面和散射系数SubsurfaceFromDiffuse将在后面实现路径积分时解释。

五、总结

体积散射效果无论是理论上还是实现上相比于普通的表面散射效果复杂了不少，关于体积渲染的实现效果和效率至今仍是图形领域的重要话题。在阅读pbrt时有几个地方不是太理解，先放着等后面回过头再来看看。

Reference

$[1]$ M, Jakob W, Humphreys G. Physically based rendering: From theory to implementation[M]. Morgan Kaufmann, 2016.