Physically Based Rendering：散射模型

光线散射模型描述了光线碰撞到物体表面时以什么方式、什么方向进行反射、折射，在这里暂时不考虑次表面散射现象。光线的反射用BRDF函数描述，而透射则用BTDF函数描述，两者统一起来称为BSDF函数（双线散射分布函数）。

  以下的内容大部分整理自pbrt第三版的第八章——REFLECTION MODELS。

一、相关术语

  物体的表面反射模型主要来源以下几个：

• 测量数据模型：通过真实世界的实验测量得到，以数据库的形式使用；
• 现象学模型：用经验公式来拟合现实世界物体表面的定性特性；
• 模拟：有时候表面组成的底层信息可以获取到，例如我们知道颜料由带颜色的附着于某些介质的粒子组成，每种粒子的反射特性我们可以知道。这种情况下我们可以模拟微观层面的光散射来模拟产生反射数据。这个过程既可以在渲染过程完成也可以作为预处理；
• 波动光学模型：将光当作波来看待，求解麦克斯韦方程；
• 几何光学模型：如果知道了表面的底层散射和几何属性，反射模型可以直接从描述中构造出来。几何光学使得光和表面的交互可追踪，许多情况下都是非常好的选择。

  目前大部分渲染算法都是基于几何光学，波动光学的复杂度相当高，其结果也未必优于几何光学。目前表面反射可以分成下图所示的四大类，从(a)到(d)分别是漫反射（diffuse）、粗糙镜面反射（glossy specular）、完美镜面反射（perfect specular）以及回归反射（retro-reflective）。大部分真实物体是这些反射类型的组合。这几种反射的区别主要在于它们的反射波瓣分布（下图中的网格描述的范围）。漫反射在半球方向上均匀地反射，这是一种理想的漫反射模型；粗糙镜面反射的反射波瓣在完美镜面反射基础上扩大了一些，用于描述金属等没那么光滑表面的反射；完美镜面反射即在非常光滑的表面上发生的反射；回归反射用于描述天鹅绒、月球等向入射方向反射的行为。

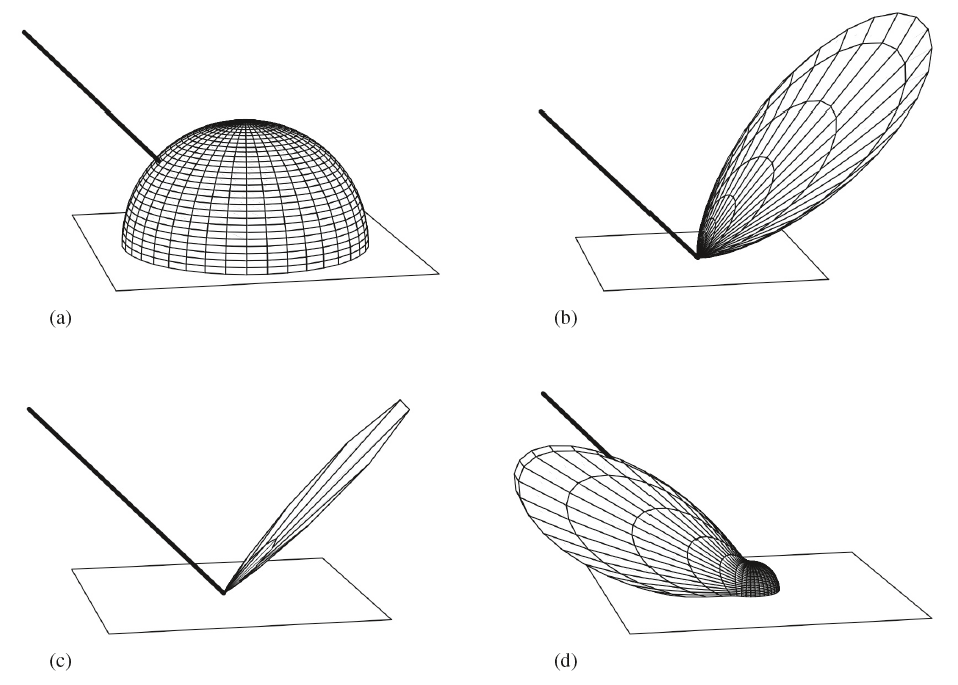
  给定一类特定的反射，反射的分布函数还可以分成各向同性（isotropic）和各向异性（anisotropic）。大部分物体的表面反射都是各项同性的，这里所谓的各向同性就是指：对于物体表面上的一点和该点对应的法线，将表面绕着该法线进行旋转，光线反射的分布情况不变（即反射波瓣保持不变）。而如果反射波瓣发生了改变，则该物体表面就是反射各向异性的，织物、光盘和拉丝金属等都属于各向异性材质。

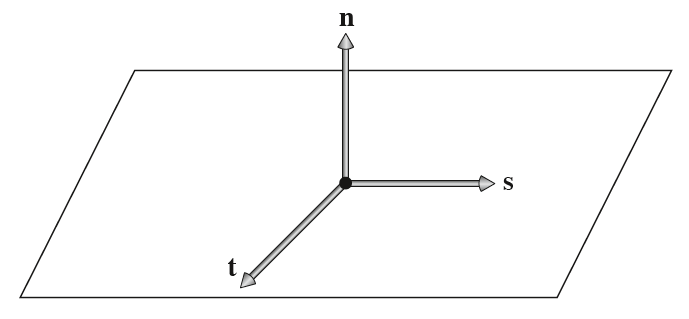
  由于通常是具体到物体表面上的一个点对散射现象进行描述，因此我们的BRDF和BTDF的计算基本上都是在物体表面上的局部坐标系下进行，这个局部坐标系我们称之为着色坐标系。该坐标系如下图所示，以切线、副切线和法线向量分别作为$x$、$y$和$z$轴。

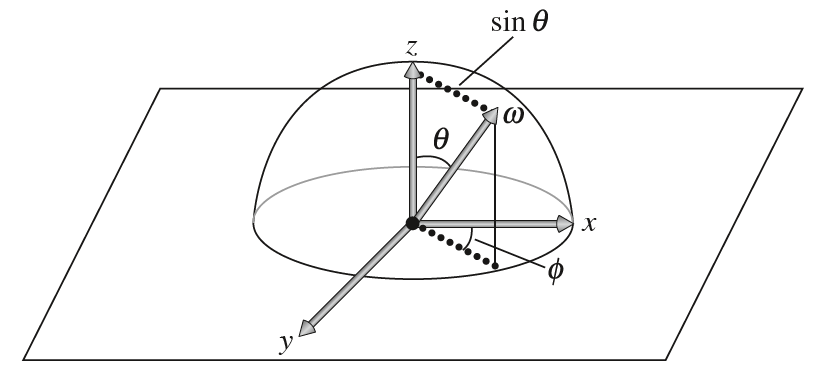
  除了笛卡尔坐标系，有时还会用到球面坐标系。一个方向向量可以用球面坐标系$(\theta,\phi)$表示，如下图所示。笛卡尔坐标和球面坐标的相互转换比较简单，这里就不赘述了。在BRDF和BTDF函数中，用$\omega_i$表示入射方向向量，而$\omega_o$表示出射方向向量，默认均已经归一化为单位向量。而且$\omega_i$和$\omega_o$默认从着色点朝向入射、出射的方向。

二、散射函数接口

  首先定义一个接口类BxDF用于作为BRDF和BTDF的接口类：

class BxDF {
  public:
    // BxDF Interface
    .....

    // BxDF Public Data
    const BxDFType type;
};

  该接口类中的type用于子类指明当前是反射还是透射，同时又属于哪类反射模型：

enum BxDFType {
    BSDF_REFLECTION = 1 << 0,
    BSDF_TRANSMISSION = 1 << 1,
    BSDF_DIFFUSE = 1 << 2,
    BSDF_GLOSSY = 1 << 3,
    BSDF_SPECULAR = 1 << 4,
    BSDF_ALL = BSDF_DIFFUSE | BSDF_GLOSSY | BSDF_SPECULAR | BSDF_REFLECTION |
               BSDF_TRANSMISSION,
};

  下面的f函数是BSDF的核心，它要求输入入射方向和反射方向（默认着色点是着色坐标系下的原点），返回相应的BSDF函数值：

virtual Spectrum f(const Vector3f &wo, const Vector3f &wi) const = 0;

  但有时我们想仅仅输入出射方向，然后根据出射方向计算入射方向并返回相应的BSDF函数值。这在完美镜面反射和粗糙镜面反射中非常有用，因为此时它们的反射波瓣很窄，只占整个半球方向很小一部分，我们不想盲目暴力地遍历所有的入射方向，而是直接根据向量的反射特性获取入射方向（对于完美镜面反射，除了此方向其他方向上的贡献均为$0$，这时的BRDF是一个狄拉克函数），省去了很大部分的计算。为此，亦声明了如下的接口：

virtual Spectrum Sample_f(const Vector3f &wo, Vector3f *wi,
                              const Point2f &sample, Float *pdf,
                              BxDFType *sampledType = nullptr) const;

  函数的其他参数我们暂时先忽略。用球面坐标系$(\theta,\phi)$表示方向向量，BSDF函数本质上是关于入射方向和散射方向的4D函数，在某些特殊情况下，我们可以将其中的入射的两个维度砍掉。一种特殊情况就是半球-方向反射率（hemispherical-directional reflectance），此时它假定半球方向的入射光强度为一个常量，即入射辐射率是一个常量函数，因此可以将反射方程中的入射辐射率$L_i$提取到半球积分外面，剩下的部分就是半球-方向反射率（即下面的公式$(1)$）。对于给定的出射方向$\omega_o$，可以直接计算入射辐照度在该方向上的反射比率如下：

$$\rho_{hd}(\omega_o)=\int_{H^2(n)} f_r(p,\omega_o, \omega_i)|cos\theta_i|d\omega_i \tag {1}$$

  上述的公式也可以被解读为：来自某个给定方向上的入射光向整个半球方向反射的总反射比率（此时$\omega_o$就变成了入射方向而非反射方向）。之所以能够这样解读，是因为基于物理的BRDF有个隐性的假设，即对称性，关于入射和反射的对称性。但需要注意BTDF并没有此类对称性。我们定义下面的rho函数接口用于计算半球-方向反射率，参数nSamples和samples用于辅助计算公式$(1)$的积分：

virtual Spectrum rho(const Vector3f &wo, int nSamples, const Point2f *samples) const;

  除了上面的半球-方向反射率之外，还有一种反射率叫做半球-半球反射率（hemispherical-hemispherical reflectance）。它计算的是：半球上所有的入射方向入射进来的辐射率都一样（即是一个常量）的情况下，表面接收到这些全部入射进来的辐照度，再向整个半球出射出去的辐照度比例（即表面出射的总能量/表面接收的总能量）：

$$\rho_{hh}=\frac{1}{\pi}\int_{H^2(n)} \int_{H^2(n)}f_r(p,\omega_o,\omega_i)|cos\theta_o cos\theta_i| d\omega_o d\omega_i \tag {2}$$

  可以理解为在公式$(1)$的基础上，再削减出射方向的维度，因此上述的公式$(2)$没有输入参数。为此，定义下面的接口用以计算公式$(2)$：

virtual Spectrum rho(int nSamples, const Point2f *samples1,
                         const Point2f *samples2) const;

  在此基础上，我们再定义创建ScaledBxDF类，它本质上就是将BxDF函数的返回值再乘上一个光谱值（RGB或者基于采样的光谱向量），这很常见（例如反射方程中的入射辐射率$L_i$和$f_r$的相乘）：

class ScaledBxDF : public BxDF {
  public:
    // ScaledBxDF Public Methods
    ScaledBxDF(BxDF *bxdf, const Spectrum &scale)
        : BxDF(BxDFType(bxdf->type)), bxdf(bxdf), scale(scale) {}
    Spectrum rho(const Vector3f &w, int nSamples,
                 const Point2f *samples) const {
        return scale * bxdf->rho(w, nSamples, samples);
    }
    Spectrum rho(int nSamples, const Point2f *samples1,
                 const Point2f *samples2) const {
        return scale * bxdf->rho(nSamples, samples1, samples2);
    }
    Spectrum f(const Vector3f &wo, const Vector3f &wi) const;
    Spectrum Sample_f(const Vector3f &wo, Vector3f *wi, const Point2f &sample,
                      Float *pdf, BxDFType *sampledType) const;
    Float Pdf(const Vector3f &wo, const Vector3f &wi) const;
    std::string ToString() const;

  private:
    BxDF *bxdf;
    Spectrum scale;
};

三、镜面反射和透射

  我们首先来看完美光滑表面上发生的镜面反射和镜面透射。完美的镜面反射和透射非常特殊，给定一个入射方向$\omega_i$，则该表面散射的方向有且仅有一个$\omega_o$，而非遍布整个半球方向。给定入射方向$\omega_i$，我们可以很容易地求出相应的完美镜面反射方向$\omega_o$，而透射方向的计算则稍微要麻烦一点。Snell定律给出介质透射指数和透射角度的关系，透射指数描述了相对于真空情况下光线在介质中的速度降低了多少，用$\eta$标记：

$$\eta_i sin\theta_i = \eta_t sin \theta_t \tag {3}$$

  实际情况下，折射系数通常与光的波长有关，随着光波的变化而变化。由此，入射光将在两种不同介质之间的边界上向多个方向发生透射，而非仅仅一个方向，这被称为色散现象（dispersion）。例如一束白光透过三棱镜将产生七彩光带，这七彩光带具有一定的范围。但在计算机图形学中，我们通常忽略这个现象，假定折射系数与波长无关，因为此种现象对于人类视觉来说不是很关键。

  除了散射方向的计算，我们还要计算光能的反射比例和折射比例，这通过菲涅尔方程联系起来。

1、菲涅尔反射方程

  菲涅尔方程（Fresnel equations）描述了一束光照射到表面上时反射的比例。值得一提的是，在完美光滑的表面上，菲涅尔方程就是麦克斯韦方程的解。给定折射系数和入射方向与法线的夹角，菲涅尔方程给出了在物体表面上产生两种不同偏振状态的反射率，两种偏振状态分别是平行偏振光和垂直偏振光。但我们忽略光的偏振现象，假定光是无偏振的，因此菲涅尔反射率应该是两种偏振状态的反射率的平均值。

  根据是否存在能够导电的自由电子，可以将物体的材质分成以下的三大类：

• 绝缘体（dielectric）：此类材质不导电，其介质的折射指数均为实数值，会透射一定量的入射光，此类材质有玻璃、矿物油、水和空气等；
• 导电体（conductor）：此类材质能够导电，因其具有自由移动的电子，此类材质不透明（一般透射进入内部的光被转换成了热能，厚度很薄的极端情况不考虑），仅发生反射。其介质的折射指数是复数值$\overline \eta=\eta + ik$；
• 半导体（semiconductor）：例如硅或锗都属于此类，在这里我们不考虑。

  绝缘体和导电体的反射率都有菲涅尔反射方程给出，但考虑到导电体的折射指数为复数的情况，有必要分类情况讨论。在此创建一个Fresnel接口类如下，Evaluate接口输入$cos\theta_i$，返回菲涅尔反射率，反射率是$[0,1]$之间的一个浮点数值：

class Fresnel {
  public:
    // Fresnel Interface
    virtual ~Fresnel();
    virtual Spectrum Evaluate(Float cosI) const = 0;
};

  首先来看入射介质与折射介质均为绝缘体的情况，此时折射指数均为实数值。设入射介质的折射指数为$\eta_i$，折射介质的折射指数为$\eta_t$，$\theta_i$和$\theta_t$分别是入射方向$\omega_i$和折射方向$\omega_t$与法线的夹角，则菲涅尔反射率计算如下：

$$r_{||}=\frac{\eta_t cos\theta_i-\eta_icos\theta_t}{\eta_tcos\theta_i+\eta_icos\theta_t} \tag {4}$$ $$r_{\perp}=\frac{\eta_i cos\theta_i-\eta_tcos\theta_t}{\eta_icos\theta_i+\eta_tcos\theta_t} \tag {5}$$

  其中$r_{||}$是平行偏振光的反射率，$r_{\perp}$是垂直偏振光的反射率。对于无偏振光，则菲涅尔反射率是两者的综合平均：

$$F_r=\frac12(r_{||}^2+r_{\perp}^2) \tag {6}$$

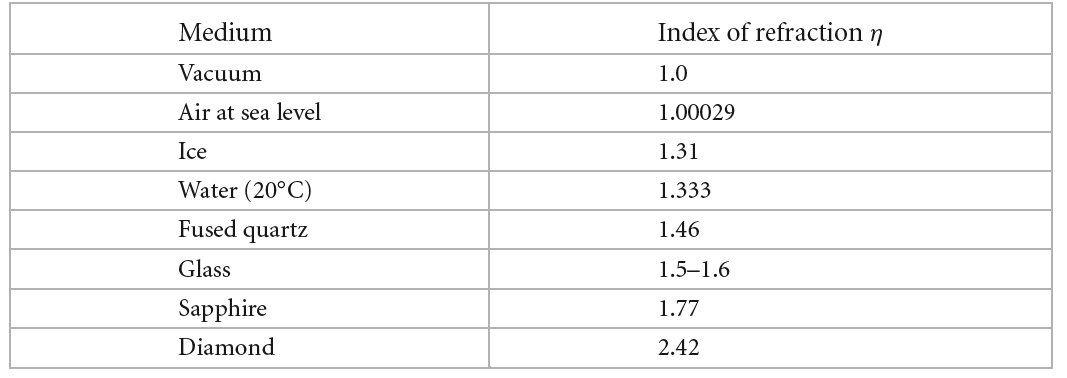
  因此，根据能量守恒定律，绝缘体的透射率为$1-F_r$。下图列出了一些常见的绝缘体的折射系数：

  根据以上讨论，可实现FrDielectric函数如下，输入参数分别为$\eta_i$、$\eta_t$和$cos\theta_i$，返回绝缘体的反射率：

Float FrDielectric(Float cosThetaI, Float etaI, Float etaT) {
    cosThetaI = Clamp(cosThetaI, -1, 1);
    // Potentially swap indices of refraction
    bool entering = cosThetaI > 0.f;
    if (!entering) {
        std::swap(etaI, etaT);
        cosThetaI = std::abs(cosThetaI);
    }

    // Compute _cosThetaT_ using Snell's law
    Float sinThetaI = std::sqrt(std::max((Float)0, 1 - cosThetaI * cosThetaI));
    Float sinThetaT = etaI / etaT * sinThetaI;

    // Handle total internal reflection
    if (sinThetaT >= 1) return 1;
    Float cosThetaT = std::sqrt(std::max((Float)0, 1 - sinThetaT * sinThetaT));
    Float Rparl = ((etaT * cosThetaI) - (etaI * cosThetaT)) /
                  ((etaT * cosThetaI) + (etaI * cosThetaT));
    Float Rperp = ((etaI * cosThetaI) - (etaT * cosThetaT)) /
                  ((etaI * cosThetaI) + (etaT * cosThetaT));
    return (Rparl * Rparl + Rperp * Rperp) / 2;
}

  在这里略提以下上面的代码，在计算之前我们首先根据$cos\theta_i$的符号判断当前是处于介质内部还是外部，如果是在内部向外部透射，则应该交换一下折射系数。此外，我们还考虑了全反射的情况，根据Snell定律计算出来的$sin\theta_t$是否大于等于$1$来判断，如果大于$1$，则返回$1.0$的反射率（即全部反射了）。由此，绝缘体的Fresnel类实现如下，直接调用FrDielectric函数：

class FresnelDielectric : public Fresnel {
  public:
    // FresnelDielectric Public Methods
    Spectrum Evaluate(Float cosThetaI) const;
    FresnelDielectric(Float etaI, Float etaT) : etaI(etaI), etaT(etaT) {}

  private:
    Float etaI, etaT;
};

Spectrum FresnelDielectric::Evaluate(Float cosThetaI) const {
    return FrDielectric(cosThetaI, etaI, etaT);
}

  紧接着来考虑导电体的介质反射率。我们仅考虑入射是绝缘体介质，透射是导电体的情况（从导电体到绝缘体的透射不考虑，因为光能被完全吸收了转化成热能，几乎很少见）。导电体的折射指数为复数值$\overline \eta=\eta+ik$，虚数部分的$k$被称为吸收系数（absorption coefficient），导电体的折射系数和吸收系数均匀波长有关。绝缘体和导电体边界上的菲涅尔反射率计算公式如下：

$$r_\perp=\frac{a^2+b^2-2a cos\theta + cos^2\theta}{a^2+b^2+2acos\theta+cos^2\theta} \tag {7}$$ $$r_{||}=r_{\perp}\frac{cos^2\theta(a^2+b^2)-2acos\theta sin^2\theta + sin^4\theta}{cos^2\theta(a^2+b^2)+2acos\theta sin^2\theta+sin^4\theta} \tag {8}$$

  其中：

$$a^2+b^2=\sqrt{(\eta^2-k^2-sin^2\theta)^2+4\eta^2k^2}$$

  而上式中的$\eta+ik=\overline \eta_t/\overline \eta_i$。由此实现导电体的FrConductor，输入$cos\theta_i$、$\overline\eta_i$、$\overline \eta_t = \eta_t+ik$，返回导电体的菲涅尔反射率，输入折射指数是一个光谱值Spectrum，因为导体的折射指数与波长有关：

Spectrum FrConductor(Float cosThetaI, const Spectrum &etai,
                     const Spectrum &etat, const Spectrum &k) {
    cosThetaI = Clamp(cosThetaI, -1, 1);
    Spectrum eta = etat / etai;
    Spectrum etak = k / etai;

    Float cosThetaI2 = cosThetaI * cosThetaI;
    Float sinThetaI2 = 1. - cosThetaI2;
    Spectrum eta2 = eta * eta;
    Spectrum etak2 = etak * etak;

    Spectrum t0 = eta2 - etak2 - sinThetaI2;
    Spectrum a2plusb2 = Sqrt(t0 * t0 + 4 * eta2 * etak2);
    Spectrum t1 = a2plusb2 + cosThetaI2;
    Spectrum a = Sqrt(0.5f * (a2plusb2 + t0));
    Spectrum t2 = (Float)2 * cosThetaI * a;
    Spectrum Rs = (t1 - t2) / (t1 + t2);

    Spectrum t3 = cosThetaI2 * a2plusb2 + sinThetaI2 * sinThetaI2;
    Spectrum t4 = t2 * sinThetaI2;
    Spectrum Rp = Rs * (t3 - t4) / (t3 + t4);

    return 0.5 * (Rp + Rs);
}

  因此，导电体的菲涅尔反射类FresnelConductor实现如下：

class FresnelConductor : public Fresnel {
  public:
    // FresnelConductor Public Methods
    Spectrum Evaluate(Float cosThetaI) const;
    FresnelConductor(const Spectrum &etaI, const Spectrum &etaT,
                     const Spectrum &k)
        : etaI(etaI), etaT(etaT), k(k) {}

  private:
    Spectrum etaI, etaT, k;
};

Spectrum FresnelConductor::Evaluate(Float cosThetaI) const {
    return FrConductor(std::abs(cosThetaI), etaI, etaT, k);
}

  接下来就根据这些接口和函数实现完美的镜面反射和完美的镜面透射。

2、完美镜面反射

  对于完美的镜面反射，给定入射辐射率$L_i(\omega_i)$，菲涅尔反射率已经给出了反射辐射率的比值，因此我们现在寻找一个完美镜面反射的BRDF函数（双向反射分布函数），使得：

$$L_o(\omega_o)=\int f_r(\omega_o, \omega_i) L_i(\omega_i)|cos\theta_i|d\omega_i =F_r(\omega_r)L_i(\omega_r)$$

  其中$\omega_r$是$\omega_o$关于表面法线$n$的反射向量。上式的意思就是，给定出射方向$\omega_o$，反射方程计算的结果应当是$\omega_o$的反射向量$\omega_r$方向上入射进来的辐射率$L_i(\omega_r)$再乘上菲涅尔反射率。这表明BRDF函数即$f_r$应当为一个狄拉克函数，仅在$\omega_r$方向取值不为零。这里说的狄拉克函数就是采样理论的冲激函数$\delta (x_0)$，$\delta(x_0)$仅在$x=x_0$上取值不为零，而且具备取样特性$\int f(x)\delta(x-x_0)dx=f(x_0)$。经过一些简单的推导，可得完美镜面反射的BRDF函数如下：

$$f_r(p,\omega_o,\omega_i)=F_r(\omega_r)\frac{\delta(\omega_i-\omega_r)}{|cos\theta_r|} \tag {10}$$

  由此，可以实现镜面反射的BRDF函数如下：

Spectrum SpecularReflection::Sample_f(const Vector3f &wo, Vector3f *wi,
                                      const Point2f &sample, Float *pdf,
                                      BxDFType *sampledType) const {
    // Compute perfect specular reflection direction
    *wi = Vector3f(-wo.x, -wo.y, wo.z);
    *pdf = 1;
    return fresnel->Evaluate(CosTheta(*wi)) * R / AbsCosTheta(*wi);
}

  因为镜面反射的BRDF是一个狄拉克函数，因此仅使用Sample_f计算BRDF值，而不是使用f接口。SpecularReflection还接收一个光谱值R，这个是物体的反照率：

class SpecularReflection : public BxDF {
  public:
    // SpecularReflection Public Methods
    SpecularReflection(const Spectrum &R, Fresnel *fresnel)
        : BxDF(BxDFType(BSDF_REFLECTION | BSDF_SPECULAR)),
          R(R),
          fresnel(fresnel) {}
    Spectrum f(const Vector3f &wo, const Vector3f &wi) const {
        return Spectrum(0.f);
    }
    Spectrum Sample_f(const Vector3f &wo, Vector3f *wi, const Point2f &sample,
                      Float *pdf, BxDFType *sampledType) const;
    Float Pdf(const Vector3f &wo, const Vector3f &wi) const { return 0; }

  private:
    // SpecularReflection Private Data
    const Spectrum R;
    const Fresnel *fresnel;
};

3、完美镜面透射

  给定折射方向$\omega_o$和入射方向$\omega_i$，描述折射光的能量占据入射光的能量分布的函数就是BTDF函数（双向透射分布函数）。根据能量守恒，透射的能量占比应为菲涅尔反射之后剩余的能量占比，即$\tau = 1-F_r(\omega_i)$，透射的辐射功率为$d\Phi_o=\tau d\Phi_i$，根据辐射率的定义，我们有：

$$L_ocos\theta_o dA d\omega_o = \tau(L_i cos\theta_i dA d\omega_i)$$

  将立体角$\omega$转换成用球面坐标系$(\theta,\phi)$表示，上述公式可写成：

$$L_o cos\theta_o dA sin\theta_o d\theta_o d\phi_o = \tau(L_i cos\theta_i dA sin\theta_i d\theta_i d\phi_i) \tag {11}$$

  然后对Snell定律即$\eta_i sin\theta_i = \eta_o sin \theta_o$得两边求关于$\theta$的微分：

$$\eta_o cos\theta_o d\theta_o = \eta_i cos\theta_i d\theta_i \to \frac{cos\theta_o d\theta_o}{cos\theta_i d\theta_i}=\frac{\eta_i}{\eta_o} \tag {12}$$

  联立$(11)$、$(12)$和Snell定律， 可得：

$$L_o \eta_i^2 d\phi_o = \tau L_i \eta_o^2 d\phi_i$$

  又因为$\phi_i=\phi_o+\pi$，故$d\phi_i=d\phi_o$，可最终简化为：

$$L_o=\tau L_i \frac{\eta_o^2}{\eta_i^2} \tag {13}$$

  由此便给出了入射辐射率与出射辐射率之间的关系。正如完美镜面反射的BRDF一样，BTDF可以得到类似的狄拉克函数形式：

$$f_t(\omega_o,\omega_i)=\frac{\eta_o^2}{\eta_i^2}(1-F_r(\omega_i))\frac{\delta(\omega_i-T(\omega_o,n))}{|cos\theta_i|} \tag {14}$$

  其中$T(\omega_o,n)$表示$\omega_o$对应的入射向量（经过完美透射）。因此实现完美镜面透射的BTDF函数如下，SpecularTransmission只考虑绝缘体的透射，因此需要借用绝缘体的菲涅尔函数FresnelDielectric，etaA和etaB分别保存了当前介质外部、内部的折射指数：

class SpecularTransmission : public BxDF {
  public:
    // SpecularTransmission Public Methods
    SpecularTransmission(const Spectrum &T, Float etaA, Float etaB,
                         TransportMode mode)
        : BxDF(BxDFType(BSDF_TRANSMISSION | BSDF_SPECULAR)),
          T(T),
          etaA(etaA),
          etaB(etaB),
          fresnel(etaA, etaB),
          mode(mode) {}
    Spectrum f(const Vector3f &wo, const Vector3f &wi) const {
        return Spectrum(0.f);
    }
    Spectrum Sample_f(const Vector3f &wo, Vector3f *wi, const Point2f &sample,
                      Float *pdf, BxDFType *sampledType) const;
    Float Pdf(const Vector3f &wo, const Vector3f &wi) const { return 0; }

  private:
    // SpecularTransmission Private Data
    const Spectrum T;
    const Float etaA, etaB;
    const FresnelDielectric fresnel;
    const TransportMode mode;
};

  Sample_f的实现基本上对应的就是前面的公式$(14)$，但要注意是否发生了全反射以及判断是从里向外透射还是从外向里透射，下面中的Refract用于计算折射向量：

Spectrum SpecularTransmission::Sample_f(const Vector3f &wo, Vector3f *wi,
                                        const Point2f &sample, Float *pdf,
                                        BxDFType *sampledType) const {
    // Figure out which $\eta$ is incident and which is transmitted
    bool entering = CosTheta(wo) > 0;
    Float etaI = entering ? etaA : etaB;
    Float etaT = entering ? etaB : etaA;

    // Compute ray direction for specular transmission
    if (!Refract(wo, Faceforward(Normal3f(0, 0, 1), wo), etaI / etaT, wi))
        return 0;
    *pdf = 1;
    Spectrum ft = T * (Spectrum(1.) - fresnel.Evaluate(CosTheta(*wi)));
    // Account for non-symmetry with transmission to different medium
    if (mode == TransportMode::Radiance) ft *= (etaI * etaI) / (etaT * etaT);
    return ft / AbsCosTheta(*wi);
}

4、综合反射与透射

  上面讨论的是仅发生完美镜面反射或仅发生完美镜面透射的情况，但现实中更多的是两者的综合作用，发生透射和发生反射的比例通过菲涅尔方程联系起来，$F_r(\omega_i)$是反射率，则$1-F_r(\omega_i)$是透射率。因此我们创建一个两者综合作用的BxDF类如下：

class FresnelSpecular : public BxDF {
  public:
    // FresnelSpecular Public Methods
    FresnelSpecular(const Spectrum &R, const Spectrum &T, Float etaA,
                    Float etaB, TransportMode mode)
        : BxDF(BxDFType(BSDF_REFLECTION | BSDF_TRANSMISSION | BSDF_SPECULAR)),
          R(R),
          T(T),
          etaA(etaA),
          etaB(etaB),
          mode(mode) {}
    Spectrum f(const Vector3f &wo, const Vector3f &wi) const {
        return Spectrum(0.f);
    }
    Spectrum Sample_f(const Vector3f &wo, Vector3f *wi, const Point2f &u,
                      Float *pdf, BxDFType *sampledType) const;
    Float Pdf(const Vector3f &wo, const Vector3f &wi) const { return 0; }

  private:
    // FresnelSpecular Private Data
    const Spectrum R, T;
    const Float etaA, etaB;
    const TransportMode mode;
};

  实现的关键就是Sample_f函数，对于菲涅尔方程给定的反射率和透射率，我们以概率的形式进行采样，具体这里暂不展开，因为涉及到了后面的蒙特卡洛的渲染积分方法。

四、Lambertian漫反射

  Lambertian漫反射是一种理想的漫反射模型，在该光照模型下，入射光能向整个半球方向均匀地反射。尽管该模型现实生活中并不存在，但视觉上足以逼近真实了。Lambertian漫反射的推导非常简单，给定一束光，向整个半球反射的反射率为前面的半球-方向反射率（即前面的公式$(1)$），即：

$$\rho_{hd}(\omega_o)=\int_{H^2(n)} f_r(p,\omega_o, \omega_i)|cos\theta_i|d\omega_i$$

  Lambertian漫反射向这个半球方向均匀地反射，则其BRDF函数是跟$\omega_o$、$\omega_i$无关的常量函数，将$f_r$提出积分外部，则剩余的积分可直接求解：

$$\int_{H^2(n)} cos\theta_i d\omega_i = \int_{H^2(n)} cos\theta_i sin\theta_i d\theta_i d\phi = \pi$$

  理想情况下，不考虑能量损耗，反射到整个半球方向的总反射率$\rho_{hd}=1$，因此有$1=\pi \times f_r$，得$f_r=\frac{1}{\pi}$，Lambertian的BRDF就是这么简单，但通常我们还要考虑物体表面的反照率（可以理解为表面颜色），故Lambertian的BRDF函数为：

$$f_r(p)=\frac{R}{\pi} \tag {15}$$

  其中$R$是物体的光谱反照率。因此实现LambertianReflection如下，f函数就是上面的公式$(15)$：

class LambertianReflection : public BxDF {
  public:
    // LambertianReflection Public Methods
    LambertianReflection(const Spectrum &R)
        : BxDF(BxDFType(BSDF_REFLECTION | BSDF_DIFFUSE)), R(R) {}
    Spectrum f(const Vector3f &wo, const Vector3f &wi) const;
    Spectrum rho(const Vector3f &, int, const Point2f *) const { return R; }
    Spectrum rho(int, const Point2f *, const Point2f *) const { return R; }

  private:
    // LambertianReflection Private Data
    const Spectrum R;
};

Spectrum LambertianReflection::f(const Vector3f &wo, const Vector3f &wi) const {
    return R * InvPi;
}

  值得一提的是rho接口，他直接返回了物体的反照率。因为向整个半球方向的总反射率为$1$，因此返回$1\times R$。这是精准的解析解，没有必要用数值方法求解。

  除了Lambertian反射，还有Lambertian透射，两者区别仅在于散射的方向。Lambertian透射向表面的下半球的方向进行均匀的透射，BTDF函数与前面的BRDF函数一样。pbrt中实现了此透射，非常简单，这里不再赘述。

五、基于微平面的散射模型

  上面讨论的几种BSDF模型都是基于理想状态的物理模型，真实物理世界很少或者可以说没有如此完美的物体表面，大部分物体的表面几乎或多或少地存在着不同程度的粗糙度。为此描述此种材质表面，基于几何光学的渲染方法提出了一种微平面（microfacet）模型，该模型基于这样的设定：任何一个物体的表面，在微观层面上都是由很多个不同朝向的光滑镜面组成，这些光滑的微平面对光的散射属性共同构成了宏观表面上的光线散射性质。

  微平面的法线朝向越与宏观表面的法线一致，则表面越光滑；反之微平面的朝向越混乱，则表面越粗糙。由此，采用微平面模型对物体表面建模涉及到两个重要的点：微平面的分布描述函数、微平面的BSDF模型。这两点共同构成了宏观物体表面的BSDF函数。微平面的排列分布通常由宏观层面的统计概率描述。微平面的光学散射则稍微要麻烦一些，这是因为在微平面的局部模型下，涉及到下图所示的三类光学效应。首先是Masking即遮蔽，反射的光线被另外的微平面挡住，从而减弱了反射光线；其次是Shadowing即阴影，一个微平面被其他微平面遮挡了，处于阴影之中；最后是Interreflection即互反射，光线在微平面之间互相反射多次，最终才抵达人眼。

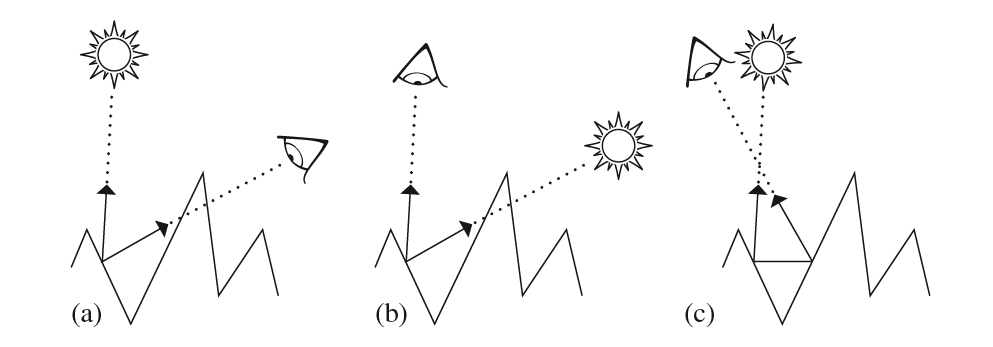
  基于微平面的BSDF模型应当尽量考虑上述三种效应，同时也尽量使得数学表达式简洁，计算量尽可能地少。

1、Oren-Nayar漫反射

  Oren和Nayar观察到真实世界的物体表面上并不存在完美的Lambertian漫反射，他们提出了一种基于球形高斯分布的V形微平面模型，用以描述粗糙的表面。他们给出的近似拟合BRDF函数如下：

$$f_r(\omega_i,\omega_o)=\frac R\pi(A+B\ max(0,cos(\phi_i-\phi_o))sin\ \alpha\ tan\ \beta) \tag {16}$$

  其中：

$$A=1-\frac{\sigma^2}{2(\sigma^2+0.33)}\\ B=\frac{0.45\sigma^2}{\sigma^2+0.09}\\ \alpha = max(\theta_i, \theta_o)\\ \beta = min(\theta_i,\theta_o)$$

  $\sigma$是微平面法线朝向的标准差，弧度制。为此，实现Oren和Nayar的漫反射BRDF函数如下：

class OrenNayar : public BxDF {
  public:
    // OrenNayar Public Methods
    Spectrum f(const Vector3f &wo, const Vector3f &wi) const;
    OrenNayar(const Spectrum &R, Float sigma)
        : BxDF(BxDFType(BSDF_REFLECTION | BSDF_DIFFUSE)), R(R) {
        sigma = Radians(sigma);
        Float sigma2 = sigma * sigma;
        A = 1.f - (sigma2 / (2.f * (sigma2 + 0.33f)));
        B = 0.45f * sigma2 / (sigma2 + 0.09f);
    }

  private:
    // OrenNayar Private Data
    const Spectrum R;
    Float A, B;
};

  根据三角恒等式，公式$(16)$中的$cos(\phi_i-\phi_o)=cos\phi_i cos\phi_o+sin\phi_i sin\phi_o$，省去了一些角度的计算。而$\alpha$和$\beta$中角度的比较可以通过它们的$cos$值比较：

Spectrum OrenNayar::f(const Vector3f &wo, const Vector3f &wi) const {
    Float sinThetaI = SinTheta(wi);
    Float sinThetaO = SinTheta(wo);
    // Compute cosine term of Oren-Nayar model
    Float maxCos = 0;
    if (sinThetaI > 1e-4 && sinThetaO > 1e-4) {
        Float sinPhiI = SinPhi(wi), cosPhiI = CosPhi(wi);
        Float sinPhiO = SinPhi(wo), cosPhiO = CosPhi(wo);
        Float dCos = cosPhiI * cosPhiO + sinPhiI * sinPhiO;
        maxCos = std::max((Float)0, dCos);
    }

    // Compute sine and tangent terms of Oren-Nayar model
    Float sinAlpha, tanBeta;
    if (AbsCosTheta(wi) > AbsCosTheta(wo)) {
        sinAlpha = sinThetaO;
        tanBeta = sinThetaI / AbsCosTheta(wi);
    } else {
        sinAlpha = sinThetaI;
        tanBeta = sinThetaO / AbsCosTheta(wo);
    }
    return R * InvPi * (A + B * maxCos * sinAlpha * tanBeta);
}

  该模型通过$\sigma$控制表面的粗糙程度。

2、法线分布函数

  在对glossy specular等表面基于微平面的BSDF进行深入了解之前，我们先来看看描述微平面分布的相关函数。微平面的分布情况主要通过微平面的法线朝向来描述，因此微平面分布函数又被称为法线分布函数，记为$D(\omega_h)$，其中输入的参数是微平面的法线向量$\omega_h$（依旧在着色坐标系下），该函数返回具有$\omega_h$朝向法线的微平面占比。法线分布函数的选取并不是任意的，需要符合物理逻辑。对于一个宏观表面上的微分面$dA$，在该微分面上的所有微平面投影到$dA$上的面积总和应该恰好等于$dA$，从数学上来讲，$D(\omega_h)$应满足如下要求：

$$\int_{H^2(n)}D(\omega_h)cos\theta_h d\omega_h = 1$$

  首先创建一个微平面函数的接口类如下，D就是微平面分布的接口函数：

class MicrofacetDistribution {
  public:
    // MicrofacetDistribution Public Methods
    virtual ~MicrofacetDistribution();
    virtual Float D(const Vector3f &wh) const = 0;
    ...

  protected:
    ...
};

  一个被广泛使用的微平面分布模型是由Beckmann和Spizzichino等人提出的微平面斜率的高斯分布函数，传统的Beckmann–Spizzichino法线分布函数定义为：

$$D(\omega_h)=\frac{e^{-tan^2\theta_h/\alpha^2}}{\pi \alpha^2 cos^4\theta_h}$$

  其中$\sigma$是微平面的RMS斜率，而$\alpha=\sqrt2 \sigma$。这是一个各向同性的法线分布函数。可将其扩展到各向异性，使得微平面的法线分布亦随着$\omega_h$的方位角（也就是$\phi_h$）变化而变化。令$\alpha_x$为法线朝向垂直于$x$轴的微平面占比，$\alpha_y$为法线朝向垂直于$y$轴的微平面占比，然后任何介于两者之间通过椭圆插值得到，故可以得到如下的各向异性微平面分布函数：

$$D(\omega_h)=\frac{e^{-tan^2\theta_h(cos^2\phi_h/\alpha_x^2+sin^2\phi_h/\alpha_y^2)}}{\pi \alpha_x \alpha_y cos^4\theta_h}$$

  当$\alpha_x=\alpha_y$时，上式就变成了各向同性函数。下面的函数实现了上述的公式，这里要特别注意$tan^2\theta_h$趋于无穷的情况：

Float BeckmannDistribution::D(const Vector3f &wh) const {
    Float tan2Theta = Tan2Theta(wh);
    if (std::isinf(tan2Theta)) return 0.;
    Float cos4Theta = Cos2Theta(wh) * Cos2Theta(wh);
    return std::exp(-tan2Theta * (Cos2Phi(wh) / (alphax * alphax) +
                                  Sin2Phi(wh) / (alphay * alphay))) /
           (Pi * alphax * alphay * cos4Theta);
}

  除了上面的法线分布函数，还有一个非常有用的微平面分布函数就是Trowbridge–Reitz法线分布函数。与Beckmann–Spizzichino函数相比，它两边趋于$0$的速度更加平缓，如下图所示：

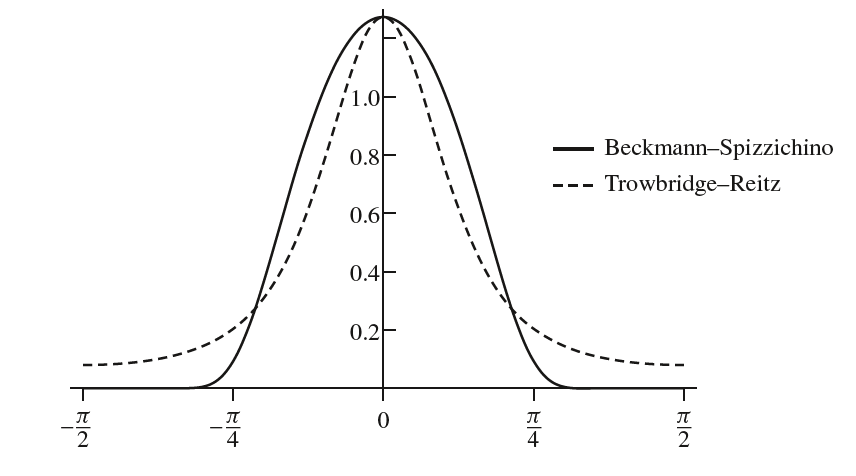
  Trowbridge–Reitz法线分布函数定义为：

$$D(\omega_h)=\frac{1}{\pi \alpha_x \alpha_y cos^4 \theta_h(1+tan^2\theta_h(cos^2\phi_h/\alpha_x^2+sin^2\phi_h/\alpha^2_y))^2}$$

Float TrowbridgeReitzDistribution::D(const Vector3f &wh) const {
    Float tan2Theta = Tan2Theta(wh);
    if (std::isinf(tan2Theta)) return 0.;
    const Float cos4Theta = Cos2Theta(wh) * Cos2Theta(wh);
    Float e =
        (Cos2Phi(wh) / (alphax * alphax) + Sin2Phi(wh) / (alphay * alphay)) *
        tan2Theta;
    return 1 / (Pi * alphax * alphay * cos4Theta * (1 + e) * (1 + e));
}

  我们用$\alpha_x$和$\alpha_y$控制微平面的分布情况，这两个参数并不是很直观。为此尝试在粗糙度和这两个参数之间构建联系，下面RoughnessToAlpha就实现了该映射，用户只需输入$[0,1]$的粗糙度，$0$表示绝对光滑，$1$表示极度粗糙，非常直观方便。

inline Float TrowbridgeReitzDistribution::RoughnessToAlpha(Float roughness) {
    roughness = std::max(roughness, (Float)1e-3);
    Float x = std::log(roughness);
    return 1.62142f + 0.819955f * x + 0.1734f * x * x + 0.0171201f * x * x * x +
           0.000640711f * x * x * x * x;
}

3、几何遮蔽函数

  前面用法线分布函数对给定粗糙程度的表面的微平面分布进行了描述，对于微平面的Shadowing效应和Masking效应，我们将采用几何遮蔽函数对此进行建模。毫无疑问，几何遮蔽函数应该是跟观察方向$\omega$相关的，给定观察方向，则因为Shadowing和Masking，只有一部分微平面能够被观察到。Smith’s masking-shadowing几何遮蔽函数$G_1(\omega, \omega_h)$给出了从$\omega$方向能够观察到的法线为$\omega_h$的微平面数量比例（因此，$0\leq G_1(\omega,\omega_h)\leq 1$）。通常情况下，几何遮蔽函数与微平面的法线$\omega_h$无关，因此写成$G_1(\omega)$的形式。

  给定观察视角$\omega$和一个微分面$dA$，则从视角$\omega$观察到的$dA$的面积是投影面积$dA cos\theta$，$\theta$是$\omega$与$dA$的法线的夹角。由此给出了下面的关于$G_1$的数学约束：

$$cos \theta=\int_{H^2(n)} G_1(\omega,\omega_h) max(0,\omega\cdot \omega_h) D(\omega_h) d\omega_h$$

  在观察方向$\omega$上，有一些正向朝向的微平面被一些背向朝向的微平面遮挡了。记$A^+(\omega)$是正向朝向$\omega$的微平面的面积和，$A^-(\omega)$是背向朝向$\omega$的微平面面积和，则应该有$cos\theta = A^+(\omega)-A^-(\omega)$，即在正向朝向的微平面中减去被遮挡的部分，则剩余部分应该就是从$\omega$能够观察到的微平面（注意，这里采用高度场表示微平面，因此是可以这样直接减去）。那么根据定义，masking-shadowing函数就应该为可见的正向朝向面积和比上总的正向朝向面积和：

$$G_1(\omega)=\frac{A^+(\omega)-A^-(\omega)}{A^+(\omega)}$$

  但masking-shadowing函数的实现通常定义了如下的辅助函数：

$$\Lambda(\omega)=\frac{A^-(\omega)}{A^+(\omega)-A^-(\omega)}=\frac{A^-(\omega)}{cos\theta}$$

  在MicrofacetDistribution中我们定义如下的接口Lambda以计算$\Lambda$这个辅助函数：

virtual Float Lambda(const Vector3f &w) const = 0;

  注意观察$\Lambda$和$G_1$的差别，我们可以根据$\Lambda$得到$G_1$：

$$G_1(\omega)=\frac{1}{1+\Lambda(\omega)}$$

Float G1(const Vector3f &w) const {
    return 1 / (1 + Lambda(w));
}

  接下来的问题就是如何根据前面的法线分布函数$D(\omega_h)$找到合适的符合数学约束的$\Lambda$函数。但实际上满足前面数学约束的$\Lambda$并不唯一，为此人们假定当前微平面的高度和周围微平面的高度不相关，这种假定虽然不符合现实，但也具备一定的准确度。

  基于上述的假设，Beckmann–Spizzichino法线分布函数的各向同性$\Lambda(\omega)$函数为：

$$\Lambda(\omega)=\frac12(erf(a)-1+\frac{e^{-a^2}}{a\sqrt\pi})$$

  其中$a=1/(\alpha tan \theta)$，$erf(x)=2/\sqrt\pi \int_0^x e^{-x’^2}dx’$是误差函数。误差函数$erf$和$exp$函数计算量有点大，pbrt用一个近似的多项式拟合上面$\Lambda(\omega)$函数，虽然带来了一定的误差，但大大提升了计算效率：

Float BeckmannDistribution::Lambda(const Vector3f &w) const {
    Float absTanTheta = std::abs(TanTheta(w));
    if (std::isinf(absTanTheta)) return 0.;
    // Compute _alpha_ for direction _w_
    Float alpha =
        std::sqrt(Cos2Phi(w) * alphax * alphax + Sin2Phi(w) * alphay * alphay);
    Float a = 1 / (alpha * absTanTheta);
    if (a >= 1.6f) return 0;
    return (1 - 1.259f * a + 0.396f * a * a) / (3.535f * a + 2.181f * a * a);
}

  这里同样用$\alpha_x$和$\alpha_y$使得$\Lambda(\omega)$为各向异性的形式。

  而Trowbridge–Reitz法线分布函数的$\Lambda(\omega)$为：

$$\Lambda(\omega)=\frac{-1+\sqrt{1+\alpha^2 tan^2\theta}}{2}$$

Float TrowbridgeReitzDistribution::Lambda(const Vector3f &w) const {
    Float absTanTheta = std::abs(TanTheta(w));
    if (std::isinf(absTanTheta)) return 0.;
    // Compute _alpha_ for direction _w_
    Float alpha =
        std::sqrt(Cos2Phi(w) * alphax * alphax + Sin2Phi(w) * alphay * alphay);
    Float alpha2Tan2Theta = (alpha * absTanTheta) * (alpha * absTanTheta);
    return (-1 + std::sqrt(1.f + alpha2Tan2Theta)) / 2;
}

  上面我们讨论的几何遮蔽函数输入一个参数，即观察方向$\omega$。但要顾及的现象除了Masking，还有Shadowing。Masking是在出射方向$\omega_o$出现了遮挡，而Shadowing则是在入射方向$\omega_i$出现了遮挡。为此，我们定义$G(\omega_o,\omega_i)$函数综合考虑Masking和Shadowing的现象，返回经过Masking和Shadowing之后的可见微平面数量比例。

  一种非常简单的$G(\omega_o,\omega_i)$直接利用前面的$G_1(\omega)$函数，假定$G_1(\omega_o)$和$G_1(\omega_i)$互相独立、互不相关，因此有如下的$G(\omega_o,\omega_i)$：

$$G(\omega_o,\omega_i)=G_1(\omega_o)G_1(\omega_i)$$

  上面的公式不难理解。但在实际情况中，$G_1(\omega_o)$和$G_1(\omega_i)$并不是互相独立的，而是具备一定的相关性。例如当$\omega_i=\omega_o$时，应该有$G(\omega_o,\omega_i)=G_1(\omega_o)=G_1(\omega_i)$，因为$G_1\leq 1$，因此$G_1(\omega_o)G_1(\omega_i)$会造成计算结果偏小。一般情况，$\omega_i$和$\omega_o$越靠近，则相关性越大。

  因此，一种更加准确的$G(\omega_o,\omega_i)$计算公式为：

$$G(\omega_o,\omega_i)=\frac{1}{1+\Lambda(\omega_o)+\Lambda(\omega_i)}$$

virtual Float G(const Vector3f &wo, const Vector3f &wi) const {
     return 1 / (1 + Lambda(wo) + Lambda(wi));
}

4、Torrance-Sparrow镜面散射

  Torrance和Sparrow提出了一种早期的、经典的BRDF模型，这类模型对金属表面进行建模。物体的表面是由大量的完美光滑的微平面组成，因此给定入射方向$\omega_i$和反射方向$\omega_o$，只有法线朝向为$\omega_i+\omega_o$的微平面会参与反射。我们称$\omega_i+\omega_o$为半角向量，记为$\omega_h$。接下来就看看Torrance-Sparrow模型是如何推导的。

  首先，根据辐射率的定义，入射到法线朝向为$\omega_h$的微平面上的总微分辐射功率为：

$$d\Phi_h =L_i(\omega_i)d\omega_i dA^{\perp}(\omega_h)=L_i(\omega_i)d\omega_i cos\theta_h dA(\omega_h)$$

  $\theta_h$是向量$\omega_i$与$\omega_h$的夹角。$dA(\omega_h)$是法线朝向为$\omega_h$的微平面总面积，又有$dA(\omega_h)=D(\omega_h)d\omega_h dA$，因此：

$$d\Phi_h=L_i(\omega_i)d\omega_i cos\theta_hD(\omega_h)d\omega_h dA \tag {17}$$

  然后，根据菲涅尔反射率，可以得到出射的辐射功率：

$$d\Phi_o=F_r(\omega_o)d\Phi_h \tag {18}$$

  再根据辐射率的定理，出射辐射率则为：

$$L(\omega_o)=\frac{d\Phi_o}{d\omega_o cos\theta_o dA}$$

  将公式$(18)$和$(17)$带入上面的方程，就有：

$$L(\omega_o)=\frac{F_r(\omega_o)L_i(\omega_i)d\omega_i D(\omega_h) d\omega_h dA cos\theta_h}{d\omega_o dA cos\theta_o}$$

  $\omega_h$和$\omega_o$又存在着函数关系，有$d\omega_h = \frac{d\omega_o}{4cos\theta_h}$（pbrt并没有在此展开，实际上应该就是通过$\omega_h=\omega_i+\omega_o$推导出来的）。带入上式有：

$$L(\omega_o)=\frac{F_r(\omega_o)L_i(\omega_i)D(\omega_h)d\omega_i}{4cos\theta_o}$$

  最后，根据BRDF的定义（即出射辐射率比上入射辐照度），加上几何遮蔽函数$G(\omega_o,\omega_i)$，我们可推得Torrance-Sparrow的BRDF公式为：

$$f_r(\omega_o,\omega_i)=\frac{D(\omega_h)G(\omega_o,\omega_i)F_r(\omega_o)}{4cos\theta_o cos\theta_i} \tag {19}$$

  Torrance-Sparrow模型优势就是它的通用性，它并不依赖于某种特定的法线分布函数以及菲涅尔方程。因此对导电体和绝缘体均适用。下面定义了MicrofacetReflection作为此类BRDF函数的实现：

class MicrofacetReflection : public BxDF {
  public:
    // MicrofacetReflection Public Methods
    MicrofacetReflection(const Spectrum &R,
                         MicrofacetDistribution *distribution, Fresnel *fresnel)
        : BxDF(BxDFType(BSDF_REFLECTION | BSDF_GLOSSY)),
          R(R),
          distribution(distribution),
          fresnel(fresnel) {}
    Spectrum f(const Vector3f &wo, const Vector3f &wi) const;
    Spectrum Sample_f(const Vector3f &wo, Vector3f *wi, const Point2f &u,
                      Float *pdf, BxDFType *sampledType) const;
    Float Pdf(const Vector3f &wo, const Vector3f &wi) const;

  private:
    // MicrofacetReflection Private Data
    const Spectrum R;
    const MicrofacetDistribution *distribution;
    const Fresnel *fresnel;
};

  其中distribution和fresnel用于微平面相关分布函数的计算。下面的f实现了上面的公式$(19)$，这里要特别注意分母的$cos\theta_i$和$cos\theta_o$是否为零：

Spectrum MicrofacetReflection::f(const Vector3f &wo, const Vector3f &wi) const {
    Float cosThetaO = AbsCosTheta(wo), cosThetaI = AbsCosTheta(wi);
    Vector3f wh = wi + wo;
    // Handle degenerate cases for microfacet reflection
    if (cosThetaI == 0 || cosThetaO == 0) return Spectrum(0.);
    if (wh.x == 0 && wh.y == 0 && wh.z == 0) return Spectrum(0.);
    wh = Normalize(wh);
    // For the Fresnel call, make sure that wh is in the same hemisphere
    // as the surface normal, so that TIR is handled correctly.
    Spectrum F = fresnel->Evaluate(Dot(wi, Faceforward(wh, Vector3f(0,0,1))));
    return R * distribution->D(wh) * distribution->G(wo, wi) * F /
           (4 * cosThetaI * cosThetaO);
}

  上面我们推导的是反射，即BRDF公式。扩展到BTDF，关键在于$d\omega_o$和$d\omega_h$之间的关系。在这里，我们考虑的是微平面上的镜面透射（而非前面的镜面反射）。给定入射向量$\omega_i$和折射向量$\omega_o$，我们同样可以得到一个半角向量$\omega_h$，只不过这个半角向量是通过Snell定律获取（对于给定的$\omega_i$和$\omega_o$，只存在法向为$\omega_h$的微平面发生了透射）。$\omega_h$的计算公式如下：

$$\omega_h=\omega_o + \eta \omega_i\\ \eta=\eta_i/\eta_o$$

  因此，$d\omega_h$与$d\omega_o$的关系为：

$$d\omega_h=\frac{\eta_o^2|\omega_o\cdot \omega_h|d\omega_o}{(\eta_i(\omega_i\cdot \omega_h)+\eta_o(\omega_o\cdot \omega_h))^2}$$

  用这个替换调用上面BRDF推导过程中的$d\omega_h$可得BTDF公式如下：

$$f_t(\omega_o,\omega_i)=\frac{\eta^2 D(\omega_h)G(\omega_o,\omega_i)(1-F_r(\omega_o))}{((\omega_o\cdot \omega_h)+\eta(\omega_i\cdot \omega_h))^2} \frac{|\omega_i\cdot \omega_h||\omega_o\cdot\omega_h|}{cos\theta_ocos\theta_i} \tag {20}$$

  因此，创建一个MicrofacetTransmission，实现公式$(20)$如下：

Spectrum MicrofacetTransmission::f(const Vector3f &wo,
                                   const Vector3f &wi) const {
    if (SameHemisphere(wo, wi)) return 0;  // transmission only

    Float cosThetaO = CosTheta(wo);
    Float cosThetaI = CosTheta(wi);
    if (cosThetaI == 0 || cosThetaO == 0) return Spectrum(0);

    // Compute $\wh$ from $\wo$ and $\wi$ for microfacet transmission
    Float eta = CosTheta(wo) > 0 ? (etaB / etaA) : (etaA / etaB);
    Vector3f wh = Normalize(wo + wi * eta);
    if (wh.z < 0) wh = -wh;

    Spectrum F = fresnel.Evaluate(Dot(wo, wh));

    Float sqrtDenom = Dot(wo, wh) + eta * Dot(wi, wh);
    Float factor = (mode == TransportMode::Radiance) ? (1 / eta) : 1;

    return (Spectrum(1.f) - F) * T *
           std::abs(distribution->D(wh) * distribution->G(wo, wi) * eta * eta *
                    AbsDot(wi, wh) * AbsDot(wo, wh) * factor * factor /
                    (cosThetaI * cosThetaO * sqrtDenom * sqrtDenom));
}

  通过微平面的完美镜面反射和透射，我们实现了glossy镜面反射和透射。

六、Ashikhmin-Shirley反射

  接下来要讨论的BRDF是由Ashikhmin和Shirley提出的一种综合了漫反射和镜面反射（glossy镜面反射）的反射模型。Ashikhmin-Shirley模型考虑如下图所示的两层表面，下面一层是漫反射材质，上面一层是glossy镜面反射材质（现实的这类物体有刷了光泽漆的墙、木桌等）。当观察方向接近于法线方向时，看到的主要下面一层的颜色；而当观察方向趋于与法向垂直时，观察道的更多是glossy镜面反射颜色。

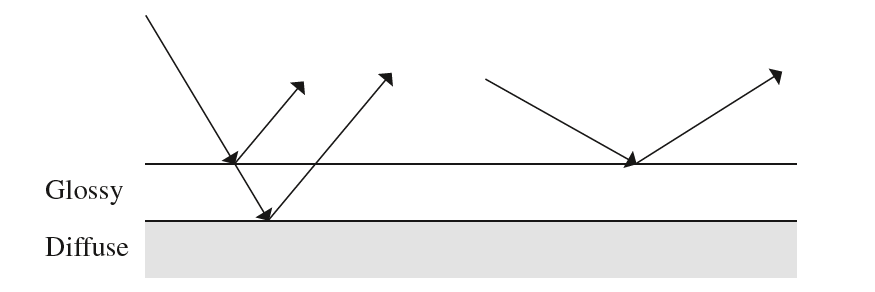
  这种表面的镜面反射和漫反射通过菲涅尔反射率联系起来。Ashikhmin-Shirley模型推导出了一种近似的Schlick菲涅尔方程如下：

$$F_r(cos\theta)=R+(1-R)(1-cos\theta)^5$$

  其中，$\theta$是观察方向与表面法线的夹角，$R$是镜面反照率光谱值。除了镜面反照率光谱值Rs，我们还有漫反射反照率光谱值Rd：

Spectrum SchlickFresnel(Float cosTheta) const {
    auto pow5 = [](Float v) { return (v * v) * (v * v) * v; };
    return Rs + pow5(1 - cosTheta) * (Spectrum(1.) - Rs);
}

  glossy镜面反射部分的BRDF如下：

$$f_r(p,\omega_o,\omega_i)=\frac{D(\omega_h)F(\omega_o)}{4(\omega_h\cdot \omega_i)(max((n\cdot \omega_o),(n\cdot \omega_i)))} \tag {21}$$

  而漫反射部分的BRDF为：

$$f_r(p,\omega_i,\omega_o)=\frac{28 R_d}{23\pi}(1-R_s)(1-(1-\frac{(n\cdot\omega_i)}{2})^5)(1-(1-\frac{(n\cdot\omega_o)}{2})^5) \tag {22}$$

  因此，Ashikhmin-Shirley模型就是上面公式$(21)$和$(22)$的综合，分别用各自的BRDF计算镜面反射辐射率、漫反射辐射率，最后总的辐射率就是两者的相加：

Spectrum FresnelBlend::f(const Vector3f &wo, const Vector3f &wi) const {
    auto pow5 = [](Float v) { return (v * v) * (v * v) * v; };
    Spectrum diffuse = (28.f / (23.f * Pi)) * Rd * (Spectrum(1.f) - Rs) *
                       (1 - pow5(1 - .5f * AbsCosTheta(wi))) *
                       (1 - pow5(1 - .5f * AbsCosTheta(wo)));
    Vector3f wh = wi + wo;
    if (wh.x == 0 && wh.y == 0 && wh.z == 0) return Spectrum(0);
    wh = Normalize(wh);
    Spectrum specular =
        distribution->D(wh) /
        (4 * AbsDot(wi, wh) * std::max(AbsCosTheta(wi), AbsCosTheta(wo))) *
        SchlickFresnel(Dot(wi, wh));
    return diffuse + specular;
}

七、傅里叶基下的BSDF查找表

  上面讨论的BSDF模型足以渲染大部分的物体材质了，但是依旧存在有些材质的BSDF无法与上述的BSDF匹配（例如多层的金属材料）。对于此类材质，一种方法就是真实测量材质的BSDF数据，然后将结果保存到一个三维或四维的查找表上，计算时直接通过查找表查找即可。但直接暴力的存储需要极其庞大的存储空间。为此研究者们提出了一种压缩方法，在傅里叶频域空间压缩存储查找表，此种方法省去了大量的存储空间。

  在这里我们仅考虑各向同性的BSDF模型。BSDF函数有两个输入参数即$\omega_i$和$\omega_o$，这两个参数转换成用球面坐标系$(\theta,\phi)$下表示，则BSDF可转变成如下形式：

$$f(\omega_i,\omega_o)=f(\mu_i,\phi_i,\mu_o,\phi_o)$$

  其中$\mu_i=cos\theta_i$，$\mu_o=cos\theta_o$。又因为BSDF为各向同性，则BSDF的取值应该至于$\phi=\phi_i-\phi_o$有关，因此：

$$f(\omega_i,\omega_o)=f(\mu_i,\mu_o,\phi_i-\phi_o)=f(\mu_i,\mu_o,\phi)$$

  各向同性的BSDF还应该是关于$\phi$的偶函数，即$f(\mu_i,\mu_o,\phi)=f(\mu_i,\mu_o,-\phi)$。根据这些属性，BSDF函数展开成如下的傅里叶级数形式：

$$f(\mu_i,\mu_o,\phi_i-\phi_o)|\mu_i|=\sum_{k=0}^{m-1}a_k(\mu_i,\mu_o)cos(k(\phi_i-\phi_o)) \tag {23}$$

  其中$a_k(\mu_i,\mu_o)$是关于给定的$(\mu_i,\mu_o)$对应的傅里叶系数。为此我们只需存储傅里叶系数$a_k(\mu_i,\mu_o)$即可，对$\mu_i$和$\mu_o$做$n$个离散量化，只需$m$个存储$n\times n$的傅里叶系数矩阵即可。但是对于给定的一对$(\mu_i,\mu_o)$，$m$的数量可以不相同，这是为了考虑空间的压缩。对于一些$(\mu_i,\mu_o)$，需要较大的$m$才能使得BSDF值达到指定的精度，而对于另一些则不需要那么大的$m$。因此我们实际上并不是存储的矩阵形式，而是对于每一对$(\mu_i,\mu_o)$和其对应的$m$，存储$a_0,a_1,…,a_{m-1}$。

  创建如下的FourierBSDFTable保存一张BSDF数据表，这个数据表从指定外部文件中读取输入：

struct FourierBSDFTable {
    // FourierBSDFTable Public Data
    Float eta;
    int mMax;
    int nChannels;
    int nMu;
    Float *mu;
    int *m;
    int *aOffset;
    Float *a;

    // FourierBSDFTable Public Methods
    static bool Read(const std::string &filename, FourierBSDFTable *table);
    ......
};

  这里提一下上面的成员变量的作用：

• eta：材质内部折射指数和外部折射指数的比值；
• mMax：公式$(23)$中的$m$的最大值；
• nChannels：指明保存的傅里叶系数是几通道的，如果是$1$通道则为单色光谱，如果是$3$通道则$a_k$分别存储的是光亮度通道、红色通道和蓝色通道；
• nMu：$\mu$的离散量化数量；
• mu：存储$\mu$的nMu个离散量化的值，为数组，从小到大有序，因此对于给定的$u$，可以使用二分查找算法；
• m：一共有nMu*nMu对$(\mu_i,\mu_o)$，每一对都有各自的$m$值，用该数组保存，大小为nMu*nMu；
• aOffset：因为对于每一对$(\mu_i,\mu_o)$，$m$的大小不一，因此有必要指出当前$(\mu_i,\mu_o)$的第一个傅里叶系数$a$得起始下标，该数组就保存了对应的起始下标，大小为nMu*nMu；
• a：保存所有的傅里叶系数。

  设$(\mu_i,\mu_o)$对应的离散量化下标为(offsetI,offsetO)，则获取对应的m和傅里叶系数的起始地址的代码如下，从该起始地址开始，后面的m个值均属于该$(\mu_i,\mu_o)$的傅里叶系数（这里说的是单色通道情况，而如果是三通道，则[0,m）为光亮度通道，[m,2m)为红色通道，[2m,3m)为蓝色通道）：

const Float *GetAk(int offsetI, int offsetO, int *mptr) const {
    *mptr = m[offsetO * nMu + offsetI];
    return a + aOffset[offsetO * nMu + offsetI];
}

  现在有个问题就是对于给定的$\mu$，找到其所在的量化区间后，如何计算其对应的傅里叶系数值（因为$\mu$很少刚刚好等于某个量化值）。这里采用Catmull-Rom样条插值，因此需要计算相应的插值权重，Catmull-Rom样条插值这里就不赘述了，下面的GetWeightsAndOffset实现了插值权重的计算，顺带计算相应的插值点的索引offset：

bool FourierBSDFTable::GetWeightsAndOffset(Float cosTheta, int *offset,
                                           Float weights[4]) const {
    return CatmullRomWeights(nMu, mu, cosTheta, offset, weights);
}

  利用$\mu_i$和$\mu_o$的双Catmull-Rom样条插值，计算$a_k$如下，以$\mu_i$为例，$o_i$就是上面计算得到的offset，$w_i$就是上面的weights：

$$a_k=\sum_{a=0}^3\sum_{b=0}^3 a_k(o_i+a,o_o+b)w_i(a)w_o(b)$$

  有了以上的铺垫，我们就可以从BSDF查找表中计算傅里叶系数，然后再用公式$(23)$计算BSDF函数值，创建一个FourierBSDF实现该BSDF函数如下，bsdfTable就是BSDF查找表：

class FourierBSDF : public BxDF {
  public:
    // FourierBSDF Public Methods
    Spectrum f(const Vector3f &wo, const Vector3f &wi) const;
    FourierBSDF(const FourierBSDFTable &bsdfTable, TransportMode mode)
        : BxDF(BxDFType(BSDF_REFLECTION | BSDF_TRANSMISSION | BSDF_GLOSSY)),
          bsdfTable(bsdfTable),
          mode(mode) {}
    Spectrum Sample_f(const Vector3f &wo, Vector3f *wi, const Point2f &u,
                      Float *pdf, BxDFType *sampledType) const;
    Float Pdf(const Vector3f &wo, const Vector3f &wi) const;

  private:
    // FourierBSDF Private Data
    const FourierBSDFTable &bsdfTable;
    const TransportMode mode;
};

  在FourierBSDF::f接口中，我们根据输入的wo和wi查找相应的傅里叶系数，然后根据这些系数计算并返回BSDF值。f的实现主要分成以下几步，首先计算$\mu_i$和$\mu_o$以及$\phi=\phi_i-\phi_o$，这里为了效率，仅计算了$cos\phi$：

Spectrum FourierBSDF::f(const Vector3f &wo, const Vector3f &wi) const {
    // Find the zenith angle cosines and azimuth difference angle
    Float muI = CosTheta(-wi), muO = CosTheta(wo);
    Float cosPhi = CosDPhi(-wi, wo);

    // Compute Fourier coefficients $a_k$ for $(\mui, \muo)$

    // Determine offsets and weights for $\mui$ and $\muo$
    ...

    // Allocate storage to accumulate _ak_ coefficients
	...

    // Accumulate weighted sums of nearby $a_k$ coefficients
    ...

    // Evaluate Fourier expansion for angle $\phi$
    ...

    // Update _scale_ to account for adjoint light transport
    ...
}

  然后，分别查找$\mu_i$和$\mu_o$对应的量化下标offsetI和offsetO以及样条插值权重weightsI和weights：

// Determine offsets and weights for $\mui$ and $\muo$
int offsetI, offsetO;
Float weightsI[4], weightsO[4];
if (!bsdfTable.GetWeightsAndOffset(muI, &offsetI, weightsI) ||
    !bsdfTable.GetWeightsAndOffset(muO, &offsetO, weightsO))
    return Spectrum(0.f);

  分配好空间，以保存接下来计算得到的$a_k$系数：

// Allocate storage to accumulate _ak_ coefficients
Float *ak = ALLOCA(Float, bsdfTable.mMax * bsdfTable.nChannels);
memset(ak, 0, bsdfTable.mMax * bsdfTable.nChannels * sizeof(Float));

  使用前面计算好的样条插值权重计算$a_0,a_1,…,a_{m-1}$：

// Accumulate weighted sums of nearby $a_k$ coefficients
int mMax = 0;
for (int b = 0; b < 4; ++b) {
    for (int a = 0; a < 4; ++a) {
        // Add contribution of _(a, b)_ to $a_k$ values
        Float weight = weightsI[a] * weightsO[b];
        if (weight != 0) {
            int m;
            const Float *ap = bsdfTable.GetAk(offsetI + a, offsetO + b, &m);
            mMax = std::max(mMax, m);
            for (int c = 0; c < bsdfTable.nChannels; ++c)
                for (int k = 0; k < m; ++k)
                    ak[c * bsdfTable.mMax + k] += weight * ap[c * m + k];
        }
    }
}

  根据$a_0,a_1,…,a_{m-1}$计算公式$\sum_{k=0}^{m-1}a_k(\mu_i,\mu_o)cos(k(\phi_i-\phi_o))$（即下面的Fourier方法），并乘上一个$1/|\mu_i|$复原BSDF函数值，如果是三通道则要多调用两次Fourier：

   // Evaluate Fourier expansion for angle $\phi$
   Float Y = std::max((Float)0, Fourier(ak, mMax, cosPhi));
   Float scale = muI != 0 ? (1 / std::abs(muI)) : (Float)0;

// Update _scale_ to account for adjoint light transport
   if (mode == TransportMode::Radiance && muI * muO > 0) {
       float eta = muI > 0 ? 1 / bsdfTable.eta : bsdfTable.eta;
       scale *= eta * eta;
   }
   if (bsdfTable.nChannels == 1)
       return Spectrum(Y * scale);
   else {
       // Compute and return RGB colors for tabulated BSDF
       Float R = Fourier(ak + 1 * bsdfTable.mMax, mMax, cosPhi);
       Float B = Fourier(ak + 2 * bsdfTable.mMax, mMax, cosPhi);
       Float G = 1.39829f * Y - 0.100913f * B - 0.297375f * R;
       Float rgb[3] = {R * scale, G * scale, B * scale};
       return Spectrum::FromRGB(rgb).Clamp();
   }

  这里略提一下Fourier的实现，它本质上就是计算$\sum_{k=0}^m a_kcos(k\phi)$，但是考虑到cos函数的计算量，这里做了一些优化。注意到$cos(k\phi)=(2cos\phi)cos((k-1)\phi)-cos((k-2)\phi)$，那么可以通过动态规划的形式从k=0开始循环，保存上两次的$cos((k-1)\phi)$和$cos((k-2)\phi)$，避免了多次调用cos函数：

Float Fourier(const Float *a, int m, double cosPhi) {
    double value = 0.0;
    // Initialize cosine iterates
    double cosKMinusOnePhi = cosPhi;
    double cosKPhi = 1;
    for (int k = 0; k < m; ++k) {
        // Add the current summand and update the cosine iterates
        value += a[k] * cosKPhi;
        double cosKPlusOnePhi = 2 * cosPhi * cosKPhi - cosKMinusOnePhi;
        cosKMinusOnePhi = cosKPhi;
        cosKPhi = cosKPlusOnePhi;
    }
    return value;
}

八、总结

  在这里我们讨论了完美镜面反射和透射的BSDF模型、Lambertian漫反射BSDF模型、Oren-Nayar漫反射模型、Torrance-Sparrow镜面散射模型、Ashikhmin-Shirley反射模型和基于查找表思想的傅里叶基形式的BSDF模型，其中Oren-Nayar漫反射模型、Torrance-Sparrow镜面散射模型和Ashikhmin-Shirley反射模型都基于微平面理论，实现了诸如glossy镜面反射、更加真实的漫反射等效果。涵盖了绝大部分的BSDF，物体的材质大都是这些BSDF模型的一个或多个的组合。

Reference

$[1]$ M, Jakob W, Humphreys G. Physically based rendering: From theory to implementation[M]. Morgan Kaufmann, 2016.