Physically Based Rendering：光谱与辐射度量

最近捡起了pbrt这本书开始阅读，之前虽然对光线追踪有所得了解，但感觉比较凌乱、不成体系，于是打算深入阅读pbrt，对离线渲染做一个深入的了解。

  以下的内容大部分整理自pbrt第三版的第五章——COLOR AND RADIOMETRY。

一、Spectral

  光谱能量分布（Spectral Power Distribution，简称为SPD）描述了光波波长的辐射功率分布情况，通常采用直角坐标系下的分布曲线来表示，横轴表示波长$\lambda$，相应地纵坐标表示单位波长间隔内的辐射功率。在计算机图形学中我们通常只关注人眼可见的光波，因而波长取值范围为$400nm-700nm$。现实世界的物体光谱能量分布可以非常复杂，为了高效、准确地描述物体的SPD，人们着手于寻找SPD的低维映射，即寻找一组基，使得可以通过这组基的系数加权来近似表示光谱能量分布情况。

  目前关于光谱表示已经有非常多的研究成果，在这里我们重点关注两个常用的光谱表示方法：基于三原色的光谱表示法和基于采样的光谱表示法。基于三原色的光谱表示法我们非常熟悉，它的表示方法是在红、绿、蓝三原色的基础上作系数加权和，这里的三原色充当着“基”的角色。此方法简单、方便、搞笑，但准确度略低。而基于采样的光谱表示法则是直接对物体的光谱能量分布曲线进行离散地采样，由于采样定理的限制，采样数量通常远多于三个，因而性能方面不如三原色法，但在物理上它更为准确。

  上面提到的两种光谱表示法都可以抽象为基于系数的光谱表示法，具体实现的区别在于“基”的不同和系数数量的不同（即维度的不同）。三原色法有三个系数，表示为一个三维向量。基于采样的光谱表示法的系数数量取决于采样数量，设采样数量为$n$，则它表现为一个$n$维向量。所以创建声明一个CoefficientSpectrum类将基于系数的光谱表示法中的公共函数等实现。

// Spectrum Declarations
template <int nSpectrumSamples>
class CoefficientSpectrum {
    // CoefficientSpectrum Public Methods
    // CoefficientSpectrum Public Data
protected:
    // CoefficientSpectrum Protected Data
    Float c[nSpectrumSamples];
};

  关于该类的实现主要是算术运算和其他的辅助运算，即加、减、乘、除、相等判断、开方、指数、对数等等，这些运算都是对向量的逐个分量做的运算，例如开放是对向量的每一个分量开发，得到的结果依旧是一个向量。比较简单，不再细说。

1、基于采样的光谱表示法

  基于采样的光谱表示法顾名思义，就是直接对SPD曲线进行采样。只考虑人眼最敏感的波长范围，我们对$[400nm,700nm]$波长范围内的光谱能量分布进行离散采样，采样得到的是一个二元组$(\lambda_i,v_i)$，即波长$\lambda_i$对应的辐射功率为$v_i$。在渲染邻域，我们取$60$为采样数量已经足够准确地描述复杂物体的光谱能量分布了，因而基于采样的光谱表示法通常是一个$60$维的向量，采样间隔为$5nm$。

static const int sampledLambdaStart = 400;
static const int sampledLambdaEnd = 700;
static const int nSpectralSamples = 60;
class SampledSpectrum : public CoefficientSpectrum<nSpectralSamples> {
  public:
    // SampledSpectrum Public Methods
  private:
    // SampledSpectrum Private Data
};

  这里我们是等间距地对波长范围进行采样。基于采样的光谱表示法首先要考虑数据的获取，通常从真实的采样数据转换而来。真实的采样数据不一定是等间距地采样，为此我们进行相应的转换。转换的思想其实很简单，例如我们需要获取$[400nm, 405nm)$对应的辐射功率值，则获取落到这个波长范围内的采样数据，计算平均值。

static SampledSpectrum FromSampled(const Float *lambda, const Float *v,
                                   int n) {
    // Sort samples if unordered, use sorted for returned spectrum
    if (!SpectrumSamplesSorted(lambda, v, n)) {
        std::vector<Float> slambda(&lambda[0], &lambda[n]);
        std::vector<Float> sv(&v[0], &v[n]);
        SortSpectrumSamples(&slambda[0], &sv[0], n);
        return FromSampled(&slambda[0], &sv[0], n);
    }
    SampledSpectrum r;
    for (int i = 0; i < nSpectralSamples; ++i) {
        // Compute average value of given SPD over $i$th sample's range
        Float lambda0 = Lerp(Float(i) / Float(nSpectralSamples),
                             sampledLambdaStart, sampledLambdaEnd);
        Float lambda1 = Lerp(Float(i + 1) / Float(nSpectralSamples),
                             sampledLambdaStart, sampledLambdaEnd);
        r.c[i] = AverageSpectrumSamples(lambda, v, n, lambda0, lambda1);
    }
    return r;
}

  计算平均值的方法也很简单，以下图为例，我们要计算$[500nm,600nm)$对应的辐射功率值，则计算落到这个范围内的样本值与横坐标构成的面积，将所有的面积加起来再除以横轴范围（这里就是$100nm$）即可。这里要注意就是边界处理情况。

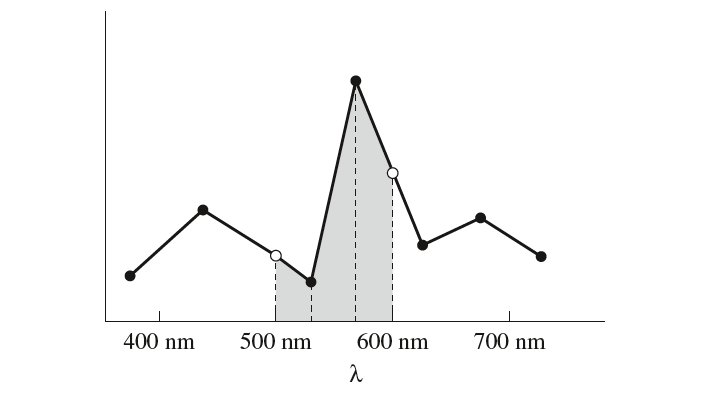
（1）转换到XYZ表色

  基于采样的光谱表示法太过耗费空间，人们发现人类视觉系统的特殊性使得仅使用三个浮点数就可以表示人类肉眼感知到的大部分颜色，这就是颜色感知三刺激理论。三刺激理论的三色理论表明，几乎所有的人类可感知的SPD能够仅仅利用三个值$x_{\lambda}$、$y_{\lambda}$和$z_{\lambda}$来表示，这个三个值分别对应着红原色刺激量、绿颜色刺激量和蓝原色刺激量，色的感觉是由于三种原色光刺激的综合结果。

  给定光谱能量分布函数$S(\lambda)$，三刺激的刺激量通过如下的公式计算：

$$x_{\lambda}=\frac{1}{\int Y(\lambda)d\lambda}\int_\lambda S(\lambda)X(\lambda)d\lambda \tag{1}$$ $$y_{\lambda}=\frac{1}{\int Y(\lambda)d\lambda}\int_\lambda S(\lambda)Y(\lambda)d\lambda \tag{2}$$ $$z_{\lambda}=\frac{1}{\int Y(\lambda)d\lambda}\int_\lambda S(\lambda)Z(\lambda)d\lambda \tag{3}$$

  其中$X(\lambda)$、$Y(\lambda)$和$Z(\lambda)$是光谱匹配曲线，如下图所示，由CIE（International Commission on illumination，CIE是法语名的简称）经过实验得到。这些曲线描述了人类视网膜中的三类视锥细胞对三种原色的刺激响应。值得注意的是，不同的光谱能量分布可能会映射到一个非常相似的三刺激值，也就是说人眼观察到不同光谱能量分布的同色光（metamers）。此外，$XYZ$表色法并不是很适用于光谱计算。

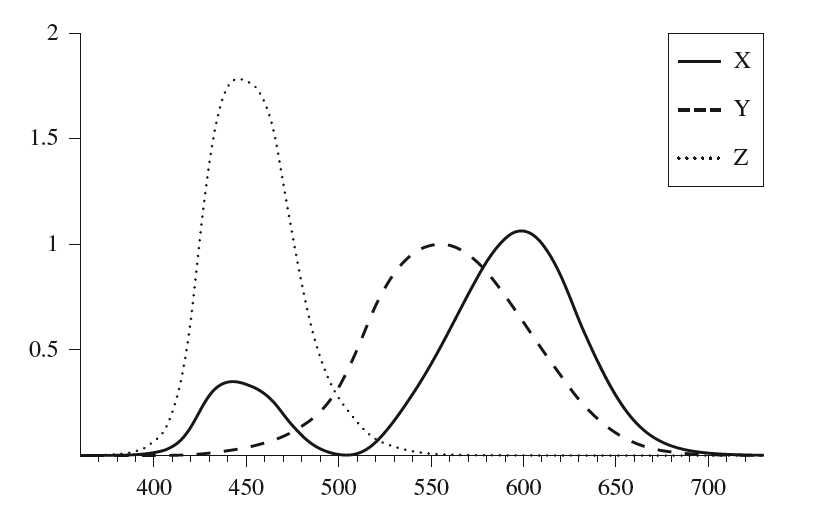
  上图中的光谱匹配曲线并没有解析的数学表达式，而是同样地通过离散采样记录保存，这里的采样间隔为$1nm$，因而采样数量为$471$。

static const int nCIESamples = 471;
extern const Float CIE_X[nCIESamples];
extern const Float CIE_Y[nCIESamples];
extern const Float CIE_Z[nCIESamples];
extern const Float CIE_lambda[nCIESamples];

  这些采样的匹配曲线同样可以看成是具体的SPD，用这些采样值初始化，得到$XYZ$匹配曲线对应的SPD，用以后续的颜色表示方法的转换。

for (int i = 0; i < nSpectralSamples; ++i) {
    Float wl0 = Lerp(Float(i) / Float(nSpectralSamples), sampledLambdaStart,
                     sampledLambdaEnd);
    Float wl1 = Lerp(Float(i + 1) / Float(nSpectralSamples), sampledLambdaStart,
                     sampledLambdaEnd);
    X.c[i] = AverageSpectrumSamples(CIE_lambda, CIE_X, nCIESamples, wl0, wl1);
    Y.c[i] = AverageSpectrumSamples(CIE_lambda, CIE_Y, nCIESamples, wl0, wl1);
    Z.c[i] = AverageSpectrumSamples(CIE_lambda, CIE_Z, nCIESamples, wl0, wl1);
}

  然后直接套用上面的转换公式即可，将积分转换成黎曼和的形式求解。注意到$\int Y(\lambda)d\lambda$与要转换的SPD无关，所以可以提前求解出来然后直接使用。

$$x_\lambda=\frac{1}{\int Y(\lambda)d\lambda}\frac{\lambda_{end}-\lambda_{start}}{N}\Sigma_{i=0}^{N-1}X_i c_i$$

static const Float CIE_Y_integral = 106.856895;
void ToXYZ(Float xyz[3]) const {
        xyz[0] = xyz[1] = xyz[2] = 0.f;
        for (int i = 0; i < nSpectralSamples; ++i) {
            xyz[0] += X.c[i] * c[i];
            xyz[1] += Y.c[i] * c[i];
            xyz[2] += Z.c[i] * c[i];
        }
        Float scale = Float(sampledLambdaEnd - sampledLambdaStart) /
                      Float(CIE_Y_integral * nSpectralSamples);
        xyz[0] *= scale;
        xyz[1] *= scale;
        xyz[2] *= scale;
}

  $XYZ$表色有个明显的作用就是它的$Y$分量，$Y$分量衡量人眼感知的颜色亮度，因而在某些场合被使用。

（2）转换到RGB表色

  上述提到的$XYZ$表色并不与我们熟悉的$RGB$表色划上等号，$XYZ$表色是完全基于人类视觉感知建立的颜色空间，而$RGB$表色则不是。$XYZ$表色系统在$RGB$系统的基础上，选用三个理想的原色来代替实际的三原色，从而将$RGB$表色系统中的光谱三刺激值$r$、$g$和$b$均变为正值。$RGB$表色系统的三原色与显示设备密切相关，在不同的显示设备之间存在差异，因而相同$rgb$在不同设备上的显示效果也存在着一定程度的差异。SPD转换到$RGB$表色并不是直接转换，而是先将其转换到$XYZ$表色，然后再转换到$RGB$表色系统。

  转换到$RGB$同样需要借助光谱响应曲线$R(\lambda)$、$G(\lambda)$和$B(\lambda)$，这些光谱响应曲线实际就是与显示设备相关的三原色光谱能量分布曲线，不同的显示设备具有不同的响应曲线：

$$r=\int R(\lambda)S(\lambda)d\lambda=\int R(\lambda)(x_\lambda X(\lambda)+y_\lambda Y(\lambda)+z_\lambda Z(\lambda))d\lambda \\ =x_\lambda \int R(\lambda)X(\lambda)d\lambda+y_\lambda \int R(\lambda)Y(\lambda)d\lambda+z_\lambda\int R(\lambda)Z(\lambda)d\lambda \tag {4}$$

  公式$(4)$给出了转换到$r$分量的公式，可以看到最终积分里面的被积公式都是可以提前知道，因此可以提前计算好然后直接使用。其他分量的计算公式类似，只需替换相应的光谱响应曲线即可，从$XYZ$到$RGB$的转换可以写成下面的矩阵向量相乘形式表示：

$$\left[\begin{matrix} r \\ g \\ b \end{matrix} \right] = \left( \begin{matrix} \int R(\lambda)X(\lambda)d\lambda & \int R(\lambda)Y(\lambda)d\lambda & \int R(\lambda)Z(\lambda)d\lambda\\ \int G(\lambda)X(\lambda)d\lambda & \int G(\lambda)Y(\lambda)d\lambda & \int G(\lambda)Z(\lambda)d\lambda\\ \int B(\lambda)X(\lambda)d\lambda & \int B(\lambda)Y(\lambda)d\lambda & \int B(\lambda)Z(\lambda)d\lambda \end{matrix} \right) \left[ \begin{matrix} x_\lambda \\ y_\lambda \\ z_\lambda \end{matrix} \right] \tag {5}$$

  矩阵内的积分值都可以提前计算好，省去极大的转换开销。这里实现了转换到高清电视的$RGB$表色系统：

inline void XYZToRGB(const Float xyz[3], Float rgb[3]) {
    rgb[0] = 3.240479f * xyz[0] - 1.537150f * xyz[1] - 0.498535f * xyz[2];
    rgb[1] = -0.969256f * xyz[0] + 1.875991f * xyz[1] + 0.041556f * xyz[2];
    rgb[2] = 0.055648f * xyz[0] - 0.204043f * xyz[1] + 1.057311f * xyz[2];
}

  相应的从$RGB$转换到$XYZ$则直接使用上述矩阵的逆矩阵即可：

inline void RGBToXYZ(const Float rgb[3], Float xyz[3]) {
    xyz[0] = 0.412453f * rgb[0] + 0.357580f * rgb[1] + 0.180423f * rgb[2];
    xyz[1] = 0.212671f * rgb[0] + 0.715160f * rgb[1] + 0.072169f * rgb[2];
    xyz[2] = 0.019334f * rgb[0] + 0.119193f * rgb[1] + 0.950227f * rgb[2];
}

  因此，从SPD转换到$RGB$表色，首先转换到$XYZ$表色，最后转换到$RGB$表色系统：

void ToRGB(Float rgb[3]) const {
        Float xyz[3];
        ToXYZ(xyz);
        XYZToRGB(xyz, rgb);
}

2、基于三原色的光谱表示法

  这里说的光谱表示法就是我们最为熟悉、最为常用的$RGB$表色系统，三原色分别是红、绿、蓝，$RGB$向量本质上是这三种原色的叠加权重。$RGB$表色系统比较简单，诸多细节不再赘述。这里提一下从$SPD$转换到$RGB$，就是先转换到$XYZ$，然后再转换到$RGB$：

static RGBSpectrum FromSampled(const Float *lambda, const Float *v, int n) {
    // Sort samples if unordered, use sorted for returned spectrum
    if (!SpectrumSamplesSorted(lambda, v, n)) {
        std::vector<Float> slambda(&lambda[0], &lambda[n]);
        std::vector<Float> sv(&v[0], &v[n]);
        SortSpectrumSamples(&slambda[0], &sv[0], n);
        return FromSampled(&slambda[0], &sv[0], n);
    }
    Float xyz[3] = {0, 0, 0};
    for (int i = 0; i < nCIESamples; ++i) {
        Float val = InterpolateSpectrumSamples(lambda, v, n, CIE_lambda[i]);
        xyz[0] += val * CIE_X[i];
        xyz[1] += val * CIE_Y[i];
        xyz[2] += val * CIE_Z[i];
    }
    Float scale = Float(CIE_lambda[nCIESamples - 1] - CIE_lambda[0]) /
                  Float(CIE_Y_integral * nCIESamples);
    xyz[0] *= scale;
    xyz[1] *= scale;
    xyz[2] *= scale;
    return FromXYZ(xyz);
}

（1）转换到SPD

  既然能够将$SPD$转换到$RGB$，人们也希望能够实现从$RGB$转换到$SPD$，但这并非那么容易。前面我们提到了不同能量分布的同色光，即不同能量分布的$SPD$转换到相近甚至相同的$RGB$，这通常是一个多对一的映射关系。所以一个$RGB$对应着无穷多个$SPD$。为此设定了几个标准用于转换：

• 如果$RGB$的全部系数均是相同的值，则转换得到的$SPD$应该是一个常量；
• 转换得到的SPD应该尽可能地光滑，因为真实世界大多数物体都具有相对光滑的$SPD$。

  一种想法是直接根据$RGB$系数对光谱响应曲线$R(\lambda)$、$G(\lambda)$和$B(\lambda)$加权叠加得到相应的$SPD$，但得到的$SPD$往往不是很光滑，因此通常并不这么做。关于这方面的内容pbrt讲述得不是很清楚，大概的做法就是为红、绿、蓝以及三原色的混合色（白、青、黄、紫红）各自计算单独的光滑SPD（可以提前计算并保存好），然后再加权混合得到。这些原色及混合色的SPD本身还可以分成反射颜色和照明颜色，这是因为照明光谱和反射光谱存在着差异。

static const int nRGB2SpectSamples = 32;
extern const Float RGB2SpectLambda[nRGB2SpectSamples];
extern const Float RGBRefl2SpectWhite[nRGB2SpectSamples];
extern const Float RGBRefl2SpectCyan[nRGB2SpectSamples];
extern const Float RGBRefl2SpectMagenta[nRGB2SpectSamples];
extern const Float RGBRefl2SpectYellow[nRGB2SpectSamples];
extern const Float RGBRefl2SpectRed[nRGB2SpectSamples];
extern const Float RGBRefl2SpectGreen[nRGB2SpectSamples];
extern const Float RGBRefl2SpectBlue[nRGB2SpectSamples];
extern const Float RGBIllum2SpectWhite[nRGB2SpectSamples];
extern const Float RGBIllum2SpectCyan[nRGB2SpectSamples];
extern const Float RGBIllum2SpectMagenta[nRGB2SpectSamples];
extern const Float RGBIllum2SpectYellow[nRGB2SpectSamples];
extern const Float RGBIllum2SpectRed[nRGB2SpectSamples];
extern const Float RGBIllum2SpectGreen[nRGB2SpectSamples];
extern const Float RGBIllum2SpectBlue[nRGB2SpectSamples];

//...

SampledSpectrum SampledSpectrum::FromRGB(const Float rgb[3],
                                         SpectrumType type) {
    SampledSpectrum r;
    if (type == SpectrumType::Reflectance) {
        // Convert reflectance spectrum to RGB
        if (rgb[0] <= rgb[1] && rgb[0] <= rgb[2]) {
            // Compute reflectance _SampledSpectrum_ with _rgb[0]_ as minimum
            r += rgb[0] * rgbRefl2SpectWhite;
            if (rgb[1] <= rgb[2]) {
                r += (rgb[1] - rgb[0]) * rgbRefl2SpectCyan;
                r += (rgb[2] - rgb[1]) * rgbRefl2SpectBlue;
            } else {
                r += (rgb[2] - rgb[0]) * rgbRefl2SpectCyan;
                r += (rgb[1] - rgb[2]) * rgbRefl2SpectGreen;
            }
        } else if (rgb[1] <= rgb[0] && rgb[1] <= rgb[2]) {
            // Compute reflectance _SampledSpectrum_ with _rgb[1]_ as minimum
            r += rgb[1] * rgbRefl2SpectWhite;
            if (rgb[0] <= rgb[2]) {
                r += (rgb[0] - rgb[1]) * rgbRefl2SpectMagenta;
                r += (rgb[2] - rgb[0]) * rgbRefl2SpectBlue;
            } else {
                r += (rgb[2] - rgb[1]) * rgbRefl2SpectMagenta;
                r += (rgb[0] - rgb[2]) * rgbRefl2SpectRed;
            }
        } else {
            // Compute reflectance _SampledSpectrum_ with _rgb[2]_ as minimum
            r += rgb[2] * rgbRefl2SpectWhite;
            if (rgb[0] <= rgb[1]) {
                r += (rgb[0] - rgb[2]) * rgbRefl2SpectYellow;
                r += (rgb[1] - rgb[0]) * rgbRefl2SpectGreen;
            } else {
                r += (rgb[1] - rgb[2]) * rgbRefl2SpectYellow;
                r += (rgb[0] - rgb[1]) * rgbRefl2SpectRed;
            }
        }
        r *= .94;
    } else {
        // Convert illuminant spectrum to RGB
        // ....
    }
    return r.Clamp();
}

二、Radiometry

  辐射度量学（Radiometry）是研究光线传播、反射等光学属性的数学工具，通过它人们构建了图形学中最为重要的渲染方程。辐射度量学是基于辐射测量原理的学科，它本质上属于几何光学的范畴（对应的是波动光学）。使用几何光学模型描述光线散射行为通常有如下的前提假设：

• 线性：光学系统中两个效果的组合等价于各自单独效果的叠加；
• 能量守恒：顾名思义，不解释；
• 无偏振：忽略电磁场的偏振效果，因此光的唯一相关属性就是波长分布；
• 不考虑荧光和磷光：不同波长的光波之间互不相干；
• 状态稳定：光在传播的过程中已经达到平衡状态，其辐射率分布不会随着时间发生变化。

  几何光学模型不能用于描述光的衍射和干涉，因此无力对此类的物理现象进行建模，相应地也就无法物理准确地实现此类现象。在图形渲染领域，用到的辐射度量学物理量主要有四个，分别是辐射通量（flux）、辐照度（irradiance）、辐射强度（intensity）和辐射率（radiance）。需要注意的是，这些辐射物理量通常是波长相关的。

1、辐射能量（Energy）

  首先从辐射能量（通常用$Q$表示）开始说起，辐射能量的单位就是焦耳（joules，简称J）。能量的定义初中物理就已经学过。光源向外辐射光子，这些光子有各自的波长取值并携带一定的能量。所有的基础辐射物理量都在用不同的方式描述辐射出来的光子。

2、辐射通量（Flux）

  辐射能量描述的仅仅是某一时间段内辐射出来的总能量，我们并不关心。我们更关注的是单位时间的辐射能量，也就是功率（Power），在这里我们也称之为辐射通量（通常用$\Phi$标记），单位为瓦特（watt，简称w），其数学定义为：

$$\Phi=lim_{\Delta t \to 0}\frac{\Delta Q}{\Delta t} = \frac{dQ}{dt} \tag {6}$$

  对于一个发光体，我们更倾向于使用功率也就是通量来描述它的发光亮度。例如$10W$的灯泡亮度明显不如$30W$的灯泡，这里就是用辐射通量来衡量。

3、辐照度（Irradiance）

  有了辐射通量之后，我们还需要描述在物体单位面积上的辐射通量，这是因为有时我们仅仅关注某一个固定区域的辐射行为。由此衍生了辐照度的定义，即单位面积上的辐射通量，符号记为$E$：

$$E(p)=lim_{\Delta A\to 0}\frac{\Delta \Phi(p)}{\Delta A}=\frac{d\Phi(p)}{dA} \tag {7}$$

  辐照度可以分成两类，分别是入射辐照度和出射辐照度，两者分别对应着入和出。入射辐照度，顾名思义就是对于一个给定区域，单位时间接收到的辐射能量；而出射辐照度就是在辐射体上的一个给定区域，单位时间辐射出去的能量。引入辐照度的概念对光照计算有非常重要的意义，以下图为例，设光源辐射通量为$\phi$，光源向四周均匀地辐射能量，因此辐射到给定半径$r$的圆上的辐照度为$E=\frac{\Phi}{4\pi r^2}$。从这个辐照度公式可以看出，半径越大则辐照度越低，这是因为光源的辐射通量是固定的，接收面积越大则平摊到单位面积上的能量越少。这个正好解释了点光源的衰减公式是距离平方的反比。

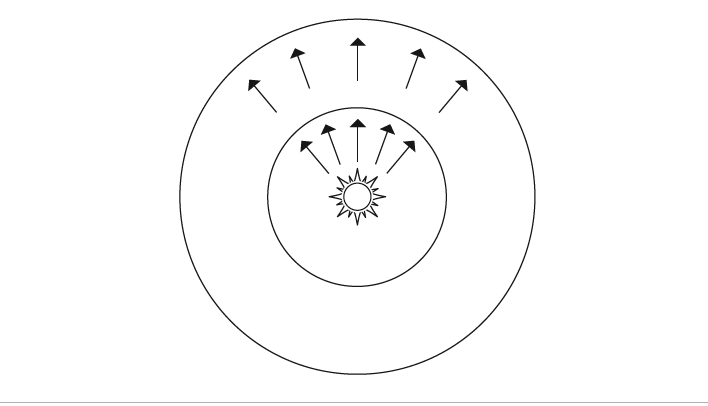
  此外，辐照度公式也解释了渲染方程中的Lambert定律（或者说余弦定律），Lambert定律指出，一定数量的光能到达物体表面的比例正比于入射方向与表面法线夹角的余弦值。这是因为辐照度的定义中的面积是必须与入射方向垂直，当表面与入射方向垂直时，入射辐照度就为$\frac{\Phi}{A}$。而当表面与入射方向不垂直的时候，就需要将表面投影到与入射方向垂直$Acos\theta$，此时辐照度为$\frac{\Phi}{Acos\theta}$。辐照度是方向无关的，可以理解成所有方向作用的结果，即从所有方向入射和向所有方向出射。

4、辐射强度（Intensity）

  在三维空间中，我们通常采用立体角来表示一定范围的方向。立体角（单位为立体弧度，简称sr）就是二维弧度角的三维推广，这里不再赘述。为什么用立体角而不是直接用方向向量？这是因为三维空间的方向有无穷多个，用立体角更加方便。辐照度衡量单位面积上的辐射通量，而相应地，辐射强度就是衡量单位立体角上的辐射通量，通常标记为$I$：

$$I=lim_{\Delta \omega\to 0}\frac{\Delta \phi}{\Delta \omega}=\frac{d\Phi}{d\omega} \tag {8}$$

  从物理意义上理解，就是在单位方向上的辐射功率。对于一个向外均匀辐射的点光源，其辐射强度是$I=\frac{\Phi}{4\pi}$。辐射强度是方向相关的，我们通常设定的点光源的辐射能量实际上是辐射强度而不是辐射通量。

5、辐射率（Radiance）

  辐照度和辐射强度分别衡量了在面积、在方向上的辐射通量分布情况，但我们需要一个物理量即衡量辐射通量在面积上的分布情况又衡量在方向上的分布情况，这就是辐射率。辐射率就是单位面积、单位立体角上的辐射通量，标记为$L$，其定义为：

$$L=\frac{d\phi}{d\omega dA} \tag {9}$$

  注意这里的$dA$是投影面积。根据入射和出射两个不同的方向，辐射率可以分别地被解读为入射辐射率和出射辐射率。解读为入射辐射率时，它可以被理解成指定在入射方向（这里说的方向通常时立体角）上的辐照度：

$$L=\frac{d\phi}{d\omega dA}=\frac{dE}{d\omega} \tag {19}$$

  如下图所示，这时$\omega$是光线入射方向，我们在入射辐照度的基础上限定了方向，可以理解为仅仅在$\omega$这个方向入射进来的辐照度，标记为$L_i(p,\omega)$。

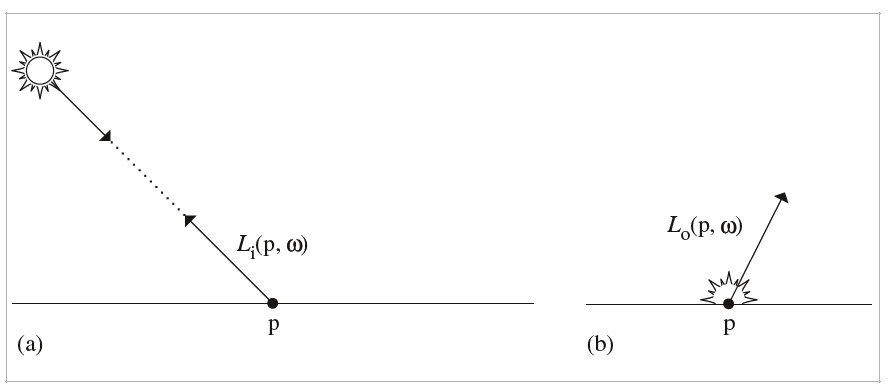
  被解读为出射辐射率的时候，可以理解成向指定的出射方向上的出射辐照度，标记为$L_o(p,\omega)$,此时$\omega$是光线的出射方向。我们计算渲染方程时，本质上就是在计算着色点在观察方向上的出射辐射率。

三、辐射积分形式的转换

  渲染方程本质上就是围绕着相关的辐射物理量做积分计算，因而其积分形式根据积分变量的不同有着不同的形式，但本质上都是一样。下面以计算辐照度的积分方程为例（注意，这并不是渲染方程）：

$$E(p,n)=\int _{\Omega} L_i(p,\omega)|cos\theta| d\omega \tag {11}$$

  计算给定着色点$p$上的辐照度就是对以法线为中心轴的半球方向的入射辐射率进行积分，$\theta$是入射方向与法线方向的夹角。这个积分公式中的积分变量是立体角$\Omega$。给定一个微分立体角$d\omega$，我们能将其转换到球面坐标系下的表示形式（如下图所示）$d\omega=sin\theta d\theta d\phi$。

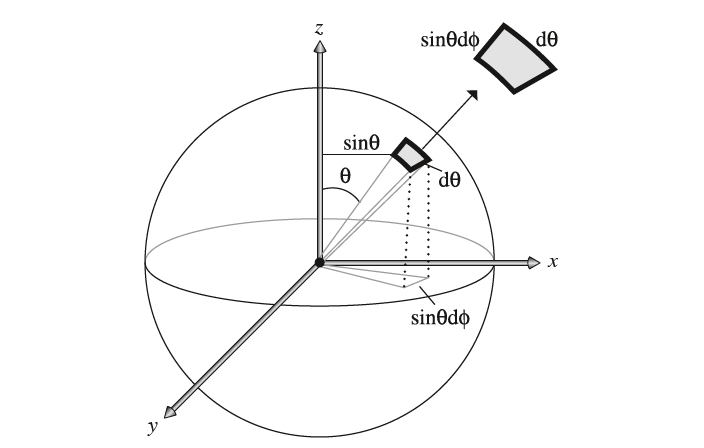
  故公式$(11)$对立体角的积分可以转换成对球面坐标$(\theta,\phi)$的双重积分形式：

$$E(p,n)=\int_{0}^{2\pi}\int_0^{\pi/2}L_i(p,\theta,\phi)cos\theta sin\theta d\theta d\phi \tag {12}$$

  公式$(11)$和$(12)$本质上是对所有的入射方向积分，但有时对方向积分不是很方便。对所有入射方向的积分等价于对所有辐射入射光的表面积分，因此有时亦转换成对面积微元的积分形式。如下图所示，考虑转换成$dA$的形式。注意到微分立体角的定义，我们有$d\omega=dA cos\theta/r^2$，这里$\theta$是$dA$表面上的法线与$p$点到$dA$向量的夹角，$r$是点$p$到$dA$的直线距离，本质上就是将$dA$投影到垂直方向，然后除以距离的平方。

$$E(p,n)=\int_A L_i cos\theta_i\frac{cos\theta_o dA}{r^2} \tag {13}$$

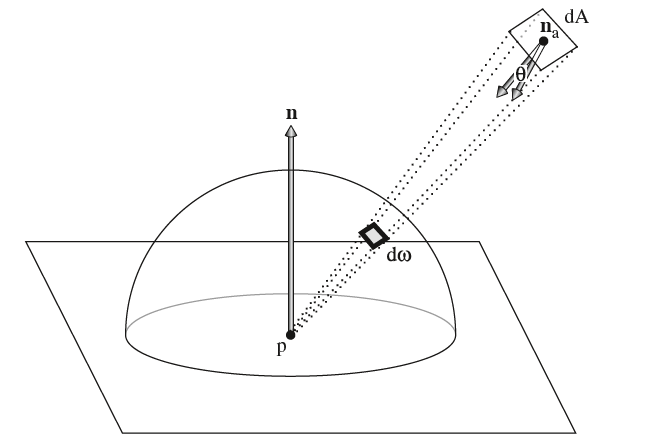
四、表面散射与次表面散射

  当一束光照射到物体表面时，会产生一系列的光线散射行为。在图形渲染领域，我们从两个主要的方面来对光线散射进行建模：散射光线的光谱分布和散射光线的方向分布。散射光线的光谱分布描述了散射光的光谱能量分布的变化，例如一道白光打到橘子上面，则白光中的蓝色光波大部分被吸收，而红色和绿色光波大部分被反射，从而反射出橘红色的外观。散射光线的方向分布描述了散射的光线在空间中的方向分布性，给定一个方向，它评估朝向这个方向散射的光线比例。这里说的散射主要包含反射、折射和次表面散射，其中反射和折射可以统称为散射，而次表面散射要复杂得多。

  针对光线的散射和次表面散射，目前主要两类数学函数对此进行描述：BSDF和BSSRDF。BSDF描述了物体表面的散射特性，仅考虑光线的反射与折射，忽略次表面散射。对于那些次表面散射效果不明显的物体来说是个非常明显的优化。而BSSRDF是一个更为通用的光线散射模型，它包含了BSDF，除此之外还考虑次表面散射的复杂效果。

1、BSDF函数

  BSDF的全称是Bidirectional Scattering Distribution Function，即双向散射分布函数。根据反射和折射的不同，BSDF又可以分为BRDF和BTDF。BRDF全称为Bidirectional Reflectance Distribution Function，即双向反射分布函数，BRDF在图形渲染领域用的最多，它描述了反射光线占据入射光线的比例。在着色点$p$上，给定入射方向$\omega_i$及入射辐射率$L_i(p,\omega_i)$，我们要计算在观察方向$\omega_o$上的出射辐射率。

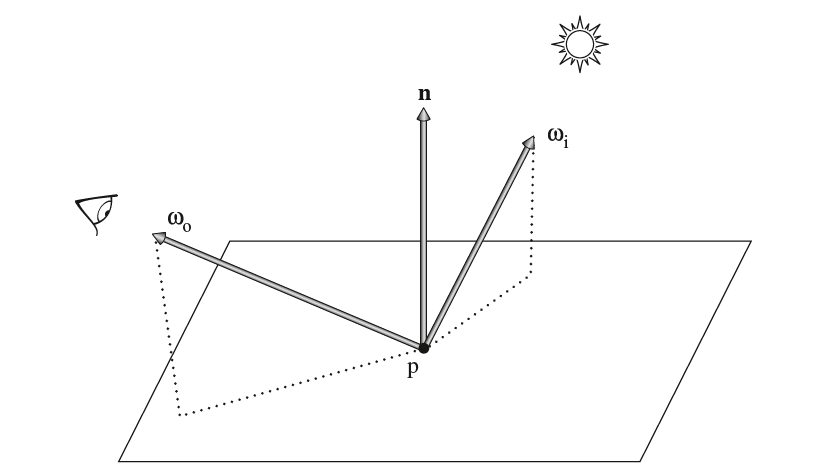
  首先可以计算$p$上的微分辐照度：

$$dE(p,\omega_i)=L_i(p,\omega_i)cos\theta_id\omega_i$$

  几何光学的线性前提指出，反射的微分辐射率应该正比于此微分辐照度：

$$dL_o(p,\omega_o)∝ dE(p,\omega_i)$$

  事实上，这个正比关系的比例就是BRDF的定义，即反射辐射率占据入射辐照度的比例，通常记为$f_r(p,\omega_o,\omega_i)$：

$$f_r(p,\omega_o,\omega_i)=\frac{dL_o(p,\omega_o)}{dE(p,\omega_i)} \tag {14}$$

  一个基于物理的BRDF应该具有如下两个重要的属性：

• 互逆性：即$f_r(p,\omega_i,\omega_o)=f_r(p,\omega_o,\omega_i)$；
• 能量守恒：反射的总能量应该不能超过入射的总能量，即要求（$H^2(n)$是半球方向）：

$$\int_{H^2(n)} f_r(p,\omega_o,\omega_i) cos\theta_i d\omega_i \leq 1$$

  而BTDF全称为Bidirectional Transmittance Distribution Function，即双向透射分布函数。它的定义与BRDF类似，只不过描述的是光线透射（折射）占据入射能量的比例，通常记为$f_t(p,\omega_o,\omega_i)$。将$f_r(p,\omega_o,\omega_i)$和$f_t(p,\omega_o,\omega_i)$综合起来就是BSDF，记为$f(p,\omega_o,\omega_i)$。有了光线的散射比例值，我们就可以计算光线散射辐射率：

$$dL_o(p,\omega_o)=f(p,\omega_o,\omega_i)L_i(p,\omega_i)|cos\theta_i|d\omega_i \tag {15}$$

  上述公式不难理解，就是在入射辐照度的基础上再乘以比例系数BSDF，得到散射的辐射率。上面公式中我们取$cos\theta_i$的绝对值，这是因为法线向量不一定与散射方向在表面的同一侧上（例如折射的时候）。综合考虑反射与透射，对着色点上的整个球体方向的出射辐射率进行积分，就可以得到最终的出射辐射率：

$$L_o(p,\omega_o)=\int_{S^2}f(p,\omega_o,\omega_i)L_i(p,\omega_i)|cos\theta_i|d\omega_i \tag {16}$$

  上述的公式就是渲染领域的最基础、最重要的方程——散射方程，它的积分定义域是整个球体方向（而非半球，因为这里综合考虑了透射）。当散射方程$(16)$仅仅考虑表面上的半球方向$H(n^2)$时，也就是仅考虑反射时，它就变成了反射方程。

2、BSSRDF函数

  可以看到BSDF函数仅考虑一个点，这个点就是着色点$p$，光线的入射、折射和反射都是直接在$p$上进行。但真实物理世界还有一个更为复杂的现象——次表面散射，简单来说就是光线从一个表面的点上进入，经过内部的散射，最终从另外一个点射出（如下图所示）。BSSRDF全称为Bidirectional Scattering Surface Reflectance Distribution Function，即双向散射表面反射分布函数，它的输入参数有四个，分别是入射方向$\omega_i$、入射点$p_i$、出射方向$\omega_o$和出射点$p_o$，通常记为$S(p_o,\omega_o,p_i,\omega_i)$。

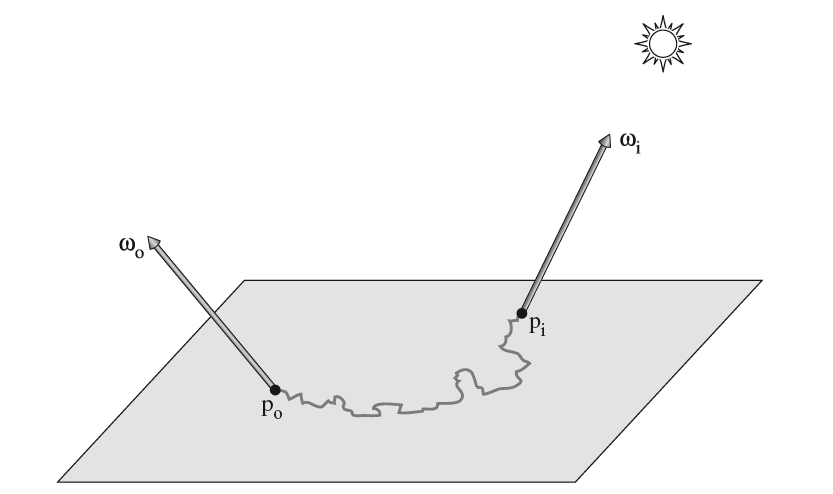
  BSSRDF定义为点出射到$p_o$的$\omega_o$方向上的微分辐射率占从$\omega_i$入射到$p_i$点的微分辐射通量的比值：

$$S(p_o,\omega_o,p_i,\omega_i)=\frac{dL_o(p_o,\omega_o)}{d\Phi(p_i,\omega_i)} \tag {17}$$

  由此可得到BSSRDF对应的渲染方程，这个渲染方程出了考虑整个半球方向，还要考虑物体的整个表面，因而是关于半球方向和表面区域的四重积分，多了两重对物体表面的积分：

$$L_o(p_o,\omega_o)=\int_A \int_{H^2(n)}S(p_o,\omega_o,p_i,\omega_i)L_i(p_i,\omega_i)|cos\theta_i|d\omega_i dA \tag {18}$$

  上述给出了物理准确的通用的渲染方程，但四重积分真的难顶。注意到随着$p_i$和$p_o$的距离增大，$S$的取值逐渐减小，因此这是一个可行优化方向。

Reference

$[1]$ M, Jakob W, Humphreys G. Physically based rendering: From theory to implementation[M]. Morgan Kaufmann, 2016.