pbrt专门有一章讲述了目前离线渲染的几种摄像机模型，图形学中的摄像机大多数为针孔摄像机模型，然而现实生活中并不存在这类的摄像机，它忽略了真实摄像头中的光穿过透镜的一些效应。为了实现景深和运动模糊的效果，需要做一些额外的设定。

  以下的内容大部分整理自pbrt第三版的第六章——CAMERA MODELS。

一、摄像机概述

  在光线追踪的渲染算法中，摄像机的主要作用就是根据采样点生成相应的采样光线，这通常涉及到几个空间的变换（通常是从成像空间变换到世界空间，与实时渲染管线相反）。在这里我们首先看看几个空间坐标系的划分，pbrt这里的坐标划分与实时渲染略有不同，但本质上都是一样，仅仅是为了方便生成采样光线而做的一些命名：

  • 物体空间：即物体自身的局部空间，不解释；
  • 世界空间：所有物体摆放的一个统一的空间，不解释；
  • 相机空间：pbrt采用了左手坐标系，因此摄像机朝向$z$轴正向，摄像机位于原点；
  • 屏幕空间：这里说的屏幕空间仅仅是投影平面空间，一般来说近平面就是投影平面，但这里不是，近平面到远平面的$z$值取值$[0,1]$，$xy$值是投影后的取值；（与实时渲染中的屏幕空间不同概念）
  • 标准空间：在屏幕空间的基础上将$xy$规范化到$[0,1]$，深度值保持不变；
  • 光栅空间：在标准空间的基础上将$xy$映射到成像分辨率范围内，即$(0,0)$到$(resolution.x, resolution.y)$，这里对应着实时渲染中的屏幕空间的概念。

  这里特别提一下一些与实时渲染的不同点，投影平面不一定就是近平面（这是合法的）。屏幕空间依旧是一个三维坐标系，因为它蕴含着深度值，而$x$和$y$是投影值。标准空间这里只是过渡，实现时并没有额外地抽离开来。摄像机主要用于生成追踪光线，通常是先将光栅空间的采样点变换到世界空间，然后在世界空间执行光线追踪算法。光栅空间的一个采样如下所示：

1
2
3
4
5
struct CameraSample {
    Point2f pFilm;
    Point2f pLens;
    Float time;
};

  pFilm就是光栅空间的采样点，其余两个变量用于实现景深和运动模糊，这里先忽略。创建一个摄像机的基类，对于一个摄像机来说，最重要的就是从世界空间到相机空间的变换矩阵，这里我们保存它的逆矩阵CameraToWorld。而film即成像胶卷，本质上就是一个二维图像类。shutterOpen和shutterClose保存相机快门的开启和关闭时间，用于模拟运动模糊效果。medium保存环境的介质类型，例如雾。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// Camera Declarations
class Camera {
  public:
    // Camera Interface
    Camera(const AnimatedTransform &CameraToWorld, Float shutterOpen,
           Float shutterClose, Film *film, const Medium *medium);
    virtual ~Camera();
    virtual Float GenerateRay(const CameraSample &sample, Ray *ray) const = 0;
    virtual Float GenerateRayDifferential(const CameraSample &sample,
                                          RayDifferential *rd) const;
    // ...other

    // Camera Public Data
    AnimatedTransform CameraToWorld;
    const Float shutterOpen, shutterClose;
    Film *film;
    const Medium *medium;
};

  这里摄像机的核心就是GenerateRay，它接收一个光栅空间的采样点，并生成相应的世界空间的采样光线，函数的返回值返回该采样光线对最终辐射率值的贡献权重。除此之外，还有GenerateRayDifferential，它除了生成采样光线，还会对光线执行一些微分操作，它把生成的光线的起始点和方向看作是光栅空间的坐标$x$和$y$的函数，对光线的起始点和方向分别在$x$和$y$方向根据偏微分的值做一定的偏移，这些偏移量蕴含了单个像素间距的采样范围，用以后续的一些抗锯齿操作（例如纹理反走样）。

  上面的摄像机仅仅包含了世界空间与相机空间的变换，我们进一步继承这个基类，实现一个投影摄像机类，它负责将三维世界投影到二维平面（或者相反的过程）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class ProjectiveCamera : public Camera {
  public:
    // ProjectiveCamera Public Methods
    ProjectiveCamera(const AnimatedTransform &CameraToWorld,
                     const Transform &CameraToScreen,
                     const Bounds2f &screenWindow, Float shutterOpen,
                     Float shutterClose, Float lensr, Float focald, Film *film,
                     const Medium *medium)
        : Camera(CameraToWorld, shutterOpen, shutterClose, film, medium),
          CameraToScreen(CameraToScreen) {
        // Initialize depth of field parameters
        lensRadius = lensr;
        focalDistance = focald;

        // Compute projective camera transformations

        // Compute projective camera screen transformations
        ScreenToRaster =
            Scale(film->fullResolution.x, film->fullResolution.y, 1) *
            Scale(1 / (screenWindow.pMax.x - screenWindow.pMin.x),
                  1 / (screenWindow.pMin.y - screenWindow.pMax.y), 1) *
            Translate(Vector3f(-screenWindow.pMin.x, -screenWindow.pMax.y, 0));
        RasterToScreen = Inverse(ScreenToRaster);
        RasterToCamera = Inverse(CameraToScreen) * RasterToScreen;
    }

  protected:
    // ProjectiveCamera Protected Data
    Transform CameraToScreen, RasterToCamera;
    Transform ScreenToRaster, RasterToScreen;
    Float lensRadius, focalDistance;
};

  这里保存了四个矩阵变换变量，名字对应着各自的空间变换，不解释。lensRadius和focalDistance用于实现景深效果，先忽略。这里我们要注意把screenWindow和film区别开来，screenWindow本质上是投影平面上的视口范围，取该平面上的最大点和最小点之间的范围；而film是光栅空间（或者说图像空间），它的取值是$(0,0)$到$(resolution.x, resolution.y)$。film和screenWindow的大小不一定相等，因此需要做一些映射，我们来看看ScreenToRaster的计算：

1
2
3
4
5
ScreenToRaster =
    Scale(film->fullResolution.x, film->fullResolution.y, 1) *
    Scale(1 / (screenWindow.pMax.x - screenWindow.pMin.x),
          1 / (screenWindow.pMin.y - screenWindow.pMax.y), 1) *
    Translate(Vector3f(-screenWindow.pMin.x, -screenWindow.pMax.y, 0));

  这里可以拆解成三个部分解读（从右到左），分别是一次平移变换和两次缩放变换。平移变换负责将窗口的左上角变换到原点。然后执行一个缩放变换，负责将投影窗口上的$x$和$y$分别映射到$[0,1]$，然后再缩放到光栅空间的取值范围内。这里注意，屏幕空间的$y$轴依旧是向上的，但光栅空间的$y$轴是朝下的，因此需要取$y$的相反数，这包含在了第一次缩放当中。

二、正交摄像机

  首先来看基于正交投影的摄像机，正交投影的相关概念非常简单，不解释。正交投影本质上相当于没有投影，因此$x$和$y$值保持不变，但这里将$z$映射到$[0,1]$。

1
2
3
Transform Orthographic(Float zNear, Float zFar) {
    return Scale(1, 1, 1 / (zFar - zNear)) * Translate(Vector3f(0, 0, -zNear));
}

  对于离线光线追踪来说，投影后的深度值没有太大的意义（不像实时渲染的z-buffer），这里之所以将$z$值做了一个映射是为了使得投影矩阵可逆，如果直接丢弃$z$那么投影矩阵将不可逆。使投影矩阵可逆是因为在这里我们基本上是使用它的逆矩阵而不是正向投影。既然深度值意义不大，所以远近平面的设置可以很随意（因为也不依靠视锥体做裁剪），pbrt这里直接将近平面和远平面设置为$z=0$和$z=1$，对超出这个范围的$z$值做投影也不会有任何的问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// OrthographicCamera Declarations
class OrthographicCamera : public ProjectiveCamera {
  public:
    // OrthographicCamera Public Methods
    OrthographicCamera(const AnimatedTransform &CameraToWorld,
                       const Bounds2f &screenWindow, Float shutterOpen,
                       Float shutterClose, Float lensRadius,
                       Float focalDistance, Film *film, const Medium *medium)
        : ProjectiveCamera(CameraToWorld, Orthographic(0, 1), screenWindow,
                           shutterOpen, shutterClose, lensRadius, focalDistance,
                           film, medium) {
        // Compute differential changes in origin for orthographic camera rays
        dxCamera = RasterToCamera(Vector3f(1, 0, 0));
        dyCamera = RasterToCamera(Vector3f(0, 1, 0));
    }
    Float GenerateRay(const CameraSample &sample, Ray *) const;
    Float GenerateRayDifferential(const CameraSample &sample,
                                  RayDifferential *) const;

  private:
    // OrthographicCamera Private Data
    Vector3f dxCamera, dyCamera;
};

  这里提一下dxCamera和dxCamera，这两个变量分别保存了光栅空间的$dx$和$dy$变换到相机空间的值，$dx$在光栅空间就是$x$轴方向的一个像素的偏移值，即Vector3f(1, 0, 0)。将这个偏移值变换到摄像机空间方便我们直接对射出的光线做一个可微偏移（GenerateRayDifferential），dy同理（之所以能够直接对偏移量做变换是因为正交投影不会改变间距和方向）。

  对于正交投影相机来说，它发射的光线的方向都是一样的，为$(0,0,1)$，区别仅在于光线的起始点不同。对光栅空间的采样点做逆变换到摄像机空间就得到了光线的起始点。最后再将光栅的起始点和方向变换到世界空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// OrthographicCamera Definitions
Float OrthographicCamera::GenerateRay(const CameraSample &sample,
                                      Ray *ray) const {
    // Compute raster and camera sample positions
    Point3f pFilm = Point3f(sample.pFilm.x, sample.pFilm.y, 0);
    Point3f pCamera = RasterToCamera(pFilm);
    *ray = Ray(pCamera, Vector3f(0, 0, 1));
    // Modify ray for depth of field
    if (lensRadius > 0) {
        // ...
    }
    ray->time = Lerp(sample.time, shutterOpen, shutterClose);
    ray->medium = medium;
    *ray = CameraToWorld(*ray);
    return 1;
}

三、透视摄像机

  对于三维图形学，透射摄像机用得更广泛一些。透视投影的相关概念这里不再赘述。首先来看下透射投影矩阵的构造，pbrt这里的透视投影固定了投影平面在$z=1$上而不是视锥的近平面，由此简化了很多东西。投影视锥由视域fovy、near和far决定。投影矩阵分为两部分，一个是投影过程，一个是缩放过程。

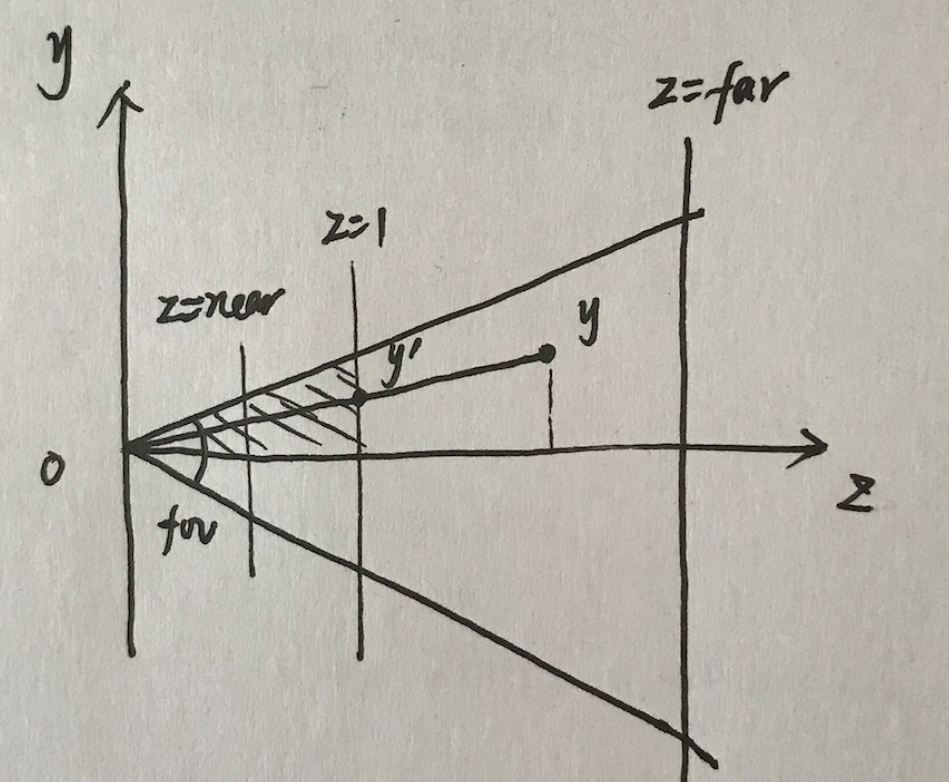
  首先是投影过程，根据三角形相似的原理就可以得到，注意成像平面是$z=1$而不是近平面。相应的还将$z$值根据近平面和远平面做缩放（意图与正交投影的一样）：

  同样地，写成齐次坐标系下的矩阵形式：

  投影到投影平面上的点再进行缩放，将$x$和$y$缩放到$[-1,1]$。因为成像平面为$z=1$，所以可以直接求出成像平面的宽度的一半为$tan(fov/2)$。所以透视投影矩阵的实现代码如下：

1
2
3
4
5
6
7
8
Transform Perspective(Float fov, Float n, Float f) {
    // Perform projective divide for perspective projection
    Matrix4x4 persp(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, f / (f - n), -f * n / (f - n),
                    0, 0, 1, 0);
    // Scale canonical perspective view to specified field of view
    Float invTanAng = 1 / std::tan(Radians(fov) / 2);
    return Scale(invTanAng, invTanAng, 1) * Transform(persp);
}

  可以看到，最后缩放的时候我们直接忽略了投影平面上的屏幕宽高的比例，对于正方形屏幕来说没有问题。而对于长方形的屏幕来说，较短的那条边被映射到$[-1,1]$，而较长的那条边会根据比例进行适当地延长（pbrt默认screenWindow的较短边长范围$[-1,1]$，较长边长按照图像的宽高等比例放大）。相应地，为了对光线微分，我们提前计算好dxCamera和dyCamera：

1
2
3
4
5
// Compute differential changes in origin for perspective camera rays
dxCamera =
    (RasterToCamera(Point3f(1, 0, 0)) - RasterToCamera(Point3f(0, 0, 0)));
dyCamera =
    (RasterToCamera(Point3f(0, 1, 0)) - RasterToCamera(Point3f(0, 0, 0)));

  这里跟正交投影部分略有不同。我们是先将光栅空间的两个相邻点做逆变换到相机空间，然后再相减，而不是直接将光栅空间的间隔做逆变换，这是因为透视投影对间隔做了扭曲了，直接对间隔变换将得到的错误的结果。然后就是根据光栅空间的采样点生成相应的光线，与正交投影相反，透射相机生成的光线方向各不相同，但起始点都一样，均为摄像机的位置（即$(0,0,0)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Float PerspectiveCamera::GenerateRay(const CameraSample &sample,
                                     Ray *ray) const {
    // Compute raster and camera sample positions
    Point3f pFilm = Point3f(sample.pFilm.x, sample.pFilm.y, 0);
    Point3f pCamera = RasterToCamera(pFilm);
    *ray = Ray(Point3f(0, 0, 0), Normalize(Vector3f(pCamera)));
    // Modify ray for depth of field
    if (lensRadius > 0) {
        // ...
    }
    ray->time = Lerp(sample.time, shutterOpen, shutterClose);
    ray->medium = medium;
    *ray = CameraToWorld(*ray);
    return 1;
}

四、环境摄像机

  除了用于观察的摄像机，还有一种摄像机模型类似于真实世界中的广角镜头。如下图所示，这种图片展现了周围$360$度所有方向的镜像，因此有一定的扭曲，此类摄像机我们称之为环境摄像机。类似于一个天空盒，把周围六个面的图像组合到一张图像中。

  实现此类摄像机不难，我们直接朝摄像机周围的所有发射追踪的光线。但是我们最终成像平面是二维的，所以需要做一定的转换。注意到所有的方向可以用中心在原点的单位球体上的所有点表示，这些方向向量可以转换成球面坐标$(\theta,\phi)$的形式，$\theta$取值范围为$[0,\pi]$，$\phi$取值$[0,2\pi]$。所以对于光栅空间的$(x,y)$，我们可以将$x$与$\phi$对应，将$y$与$\theta$对应，由此对所有的方向进行采样。

  三维方向向量和球面坐标向量的互相转换不难，这里不再赘述。值得一提的是，此类摄像机渲染出来的图像通常用于IBL，即Image Basde Lighting，基于图像的光照。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// EnvironmentCamera Method Definitions
Float EnvironmentCamera::GenerateRay(const CameraSample &sample,
                                     Ray *ray) const {
    ProfilePhase prof(Prof::GenerateCameraRay);
    // Compute environment camera ray direction
    Float theta = Pi * sample.pFilm.y / film->fullResolution.y;
    Float phi = 2 * Pi * sample.pFilm.x / film->fullResolution.x;
    Vector3f dir(std::sin(theta) * std::cos(phi), std::cos(theta),
                 std::sin(theta) * std::sin(phi));
    *ray = Ray(Point3f(0, 0, 0), dir, Infinity,
               Lerp(sample.time, shutterOpen, shutterClose));
    ray->medium = medium;
    *ray = CameraToWorld(*ray);
    return 1;
}

五、薄透镜近似模型

  真实的摄像机往往涉及到光圈的概念，这个所谓的光圈就是摄像机中的透镜。一般情况下，光圈越大则越多光线可以进入摄像机到达成像胶卷，因此需要的曝光时间比较短。真实的针孔摄像机并不是没有光圈，只是它的光圈非常小，这意味着它需要的曝光时间比较长，因此如果在曝光时间内拍摄的物体在移动或相机在移动，则得到的照片会出现运动模糊（motion blur）的效果。但光圈越大，则越容易出现景深（depth of field）的模糊效果，此时相机聚焦在一个平面上，其他的距离这个聚焦平面越远的物体将越模糊（失焦）。

  为了实现真实摄像机的聚焦和失焦（即景深）效果，针对图形渲染领域的投影类相机，人们提出了薄透镜近似模型（thin lens approximation）。在薄透镜近似模型中，我们直接忽略透镜的厚度，因为相对于半径它的厚度可以直接忽略。以下全部的内容都是关于薄透镜近似模型。

  平行的光线穿过透镜，将在透镜后面聚焦到一个点上，这个点被称为焦点（focal point）。焦点到透镜的直线距离被称为焦长（focal length），注意不是焦距。将一个成像平面放置在焦点处，则无穷远处的物体在成像平面上处于聚焦状态，因为无穷远处的物体发出或散射的光线无限逼近于平行光线。

  现假设透镜处于$z$轴原点处，其焦长为$f$，则对于场景中深度为$z$的聚焦平面的距离$z’$的计算可采用高斯透镜方程（如下所示），这表示如果要让$z$处的物体聚焦，则成像平面应放置$z’$处：

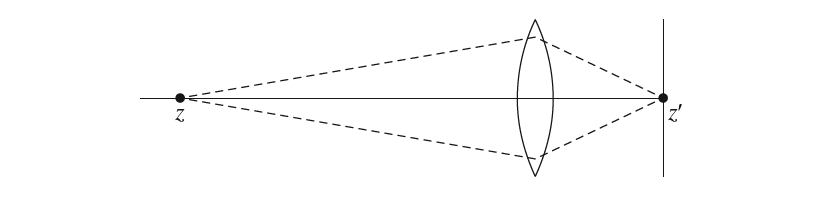
  对于那些不在$z$处的物体，其聚焦的焦点并不在$z’$处，因此处于失焦状态，它聚焦到$z’$处成像平面上的是一个圆盘而非一个聚焦点，这个圆盘我们称之为弥散圆（circle of confusion）。弥散圆的大小取决于光圈的半径、焦距（focal distance，这里就是$z’$）和物体到透镜的距离。聚焦物体到透镜的距离我们称之为景深（depth of field），透镜到成像平面的距离我们称之为焦距（而非焦长）。

  假设，景深为$z_f$，相应的成像平面在$z_f’$。则对于$z$处的点，其弥散圆如何确定？如下图(a)所示，$z’$是$z$处的焦点，透镜后方的两条虚线与成像平面$z_f’$的相交构成了弥散圆。

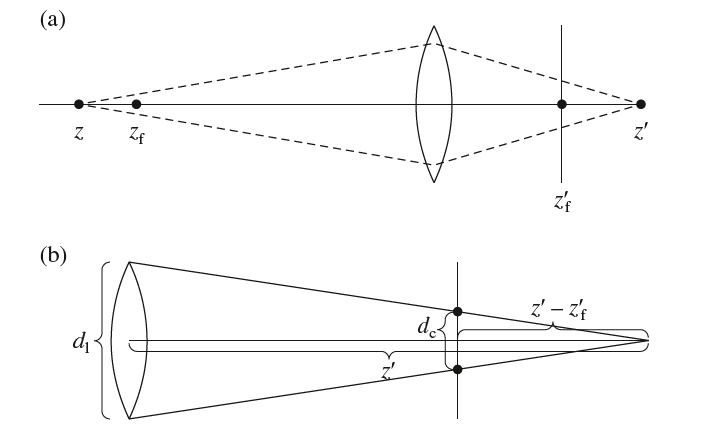
  由此，我们可以根据相似三角形原理计算弥散圆的直径。如上图(b)所示，设光圈直径为$d_1$，而弥散圆直径为$d_c$，其计算公式如下：

  将前面的高斯透镜方程带入可得：

  上述公式中，$d_1$是光圈直径，$f$焦长，$z_f$景深，$z$场景的物体。这个公式表明，聚焦的前与后的模糊不是对称的。一般在聚焦前面的物体模糊速度更快。光圈越大，则弥散圆越大，相应地更模糊。说了这么多，其实在光线追踪里面实现薄透镜模型非常简单。

  对于没有实现薄透镜模型的投影摄像机，我们可以将其透镜看成一个点，这个点就是摄像机的眼睛。那么对于要实现薄透镜模型的摄像机，其透镜不再是一个点，而是一个具有一定大小的圆盘，这个圆盘就是光圈。在这里，成像平面介于光圈和场景物体之间。如下图所示，我们在这个光圈上随机采样一个点作为射线的起始点，连接成像平面上的采样点作为射线方向。

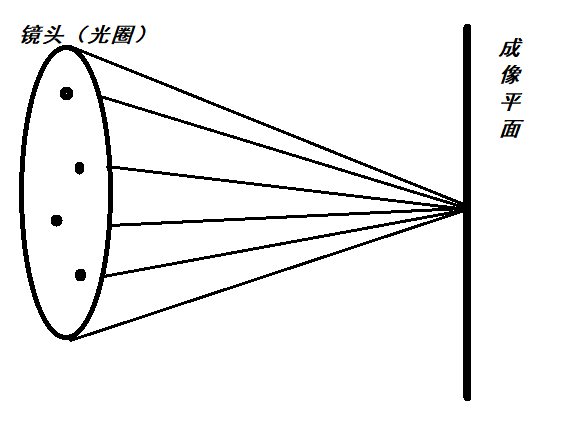
  我们有两个参数，分别是光圈半径lensRadius和焦距focalDistance，焦距就是光圈到成像平面的距离。在没有实现薄透镜近似模型时我们默认成像平面在$z=1$处。现在加入了焦距参数，我们要重新计算成像平面上的点，方法就是计算原来的射线与z=focalDistance的交点，在摄像机空间做这些很简单，不解释，$t=focalDistance/d_z$，$d_z$是原来射线的方向向量的$z$分量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Float PerspectiveCamera::GenerateRay(const CameraSample &sample,
                                     Ray *ray) const {
    // Compute raster and camera sample positions
    // ...
    // Modify ray for depth of field
    if (lensRadius > 0) {
        // Sample point on lens
        Point2f pLens = lensRadius * ConcentricSampleDisk(sample.pLens);

        // Compute point on plane of focus
        Float ft = focalDistance / ray->d.z;
        Point3f pFocus = (*ray)(ft);

        // Update ray for effect of lens
        ray->o = Point3f(pLens.x, pLens.y, 0);
        ray->d = Normalize(pFocus - ray->o);
    }
	// ...
    return 1;
}

  ConcentricSampleDisk负责在圆盘上随机采样一个点。我们用随机采样来近似实现真实相机的光圈效应，这使得我们必须提升每个像素发射的采样光线数量，否则将出现严重的噪声。

Reference

$[1]$ M, Jakob W, Humphreys G. Physically based rendering: From theory to implementation[M]. Morgan Kaufmann, 2016.

 上一页

Computer Graphics Ray Tracer

 评论


博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本站使用 Material X 作为主题 ， 总访问量为 次 。
载入天数...载入时分秒...