又是好久没更新博客了,最近在写算法分析与设计课程的期末作业,作业的题目随意,我就随兴写了烟花粒子的四叉树可视化程序和光追渲染器的八叉树求交优化。之前写的光追渲染器对每个三角网格模型的求交都是暴力遍历所有的三角形,对于三角形数量很多的模型来说效率非常低,所以我捡起了这个渲染器并为每个三角网格模型构建一颗八叉树加快射线与三角形的求交速度。还真别说,性能提升巨大。所以这篇博客本质上是一个期末作业。最后,新年快乐!

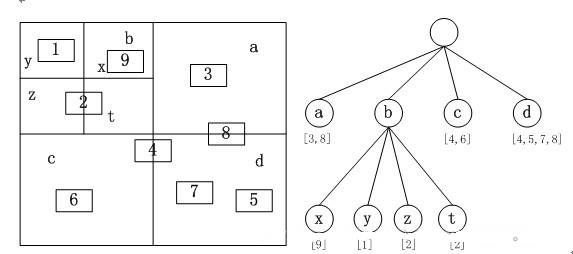
分治算法因其巧妙的算法思想能够将算法的时间复杂度降低到一个非常低的程度,例如广为流传的二分搜索算法将线性搜索时间复杂度$O(n)$降低到了$O(log\ n)$,这是一个极其恐怖的性能提升。诸多的实际应用领域例如计算机图形学、计算机视觉都有着分治算法的身影。在这里我们将重点关注计算机图形学领域非常实用、好用、高效的分治算法——四叉树空间分割算法和八叉树空间分割算法,二分搜索算法本质上处理的是一维的数据,但在图形学领域我们通常面临的是二维或者三维的点和向量,而且在实际应用中这些数据的量都非常庞大(几百万个点的点云、高精度的网格模型等等),因此为了加速这些更高维数据的搜索,一些高效的数据结构算法被提出,其中四叉树和八叉树算法就是其中之一。(当然也有高维的二叉树,例如k-d树)
一、背景介绍
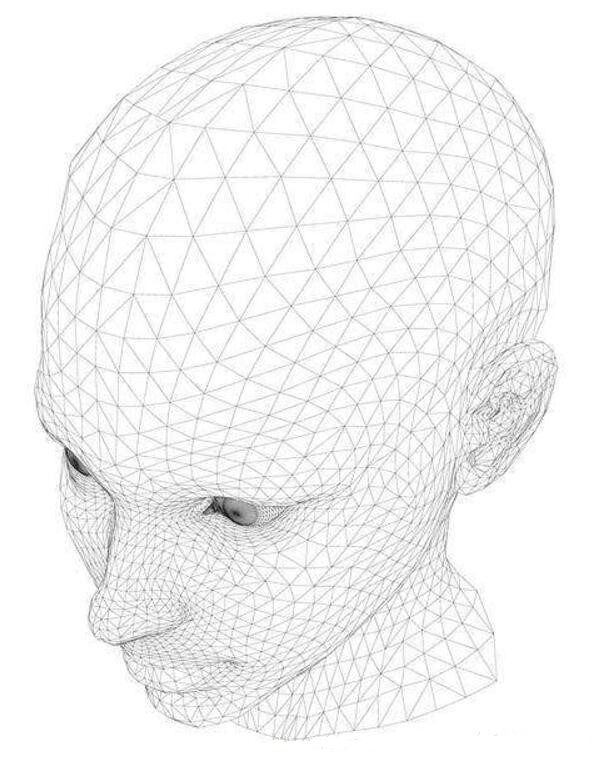
我们先来看一下算法的应用背景,计算机图形学领域研究的主要内容就是关于二维三维空间的图形绘制、物理模拟、几何建模、电脑动画等等可视化课题,目前最为流行的模型表示方法就是采用三角形网格模型,即每个网格面采用一个三角形来表示,如下图1所示:
1 | struct TreeNode |
1 | TreeNode * QuadTree::recursiveBuild(unsigned int depth, glm::vec2 min, glm::vec2 max, |
1 | void QuadTree::recursiveDestory(TreeNode *node) |
1 | bool QuadTree::recursiveInsert(unsigned int depth, TreeNode * node, |
1 | bool QuadTree::recursiveRemove(unsigned int depth, TreeNode * node, glm::vec2 min, glm::vec2 max, glm::vec2 object) |
1 | void QuadTree::recursiveTraverse(TreeNode *node, glm::vec2 min, glm::vec2 max, std::vector<glm::vec2>& lines) |
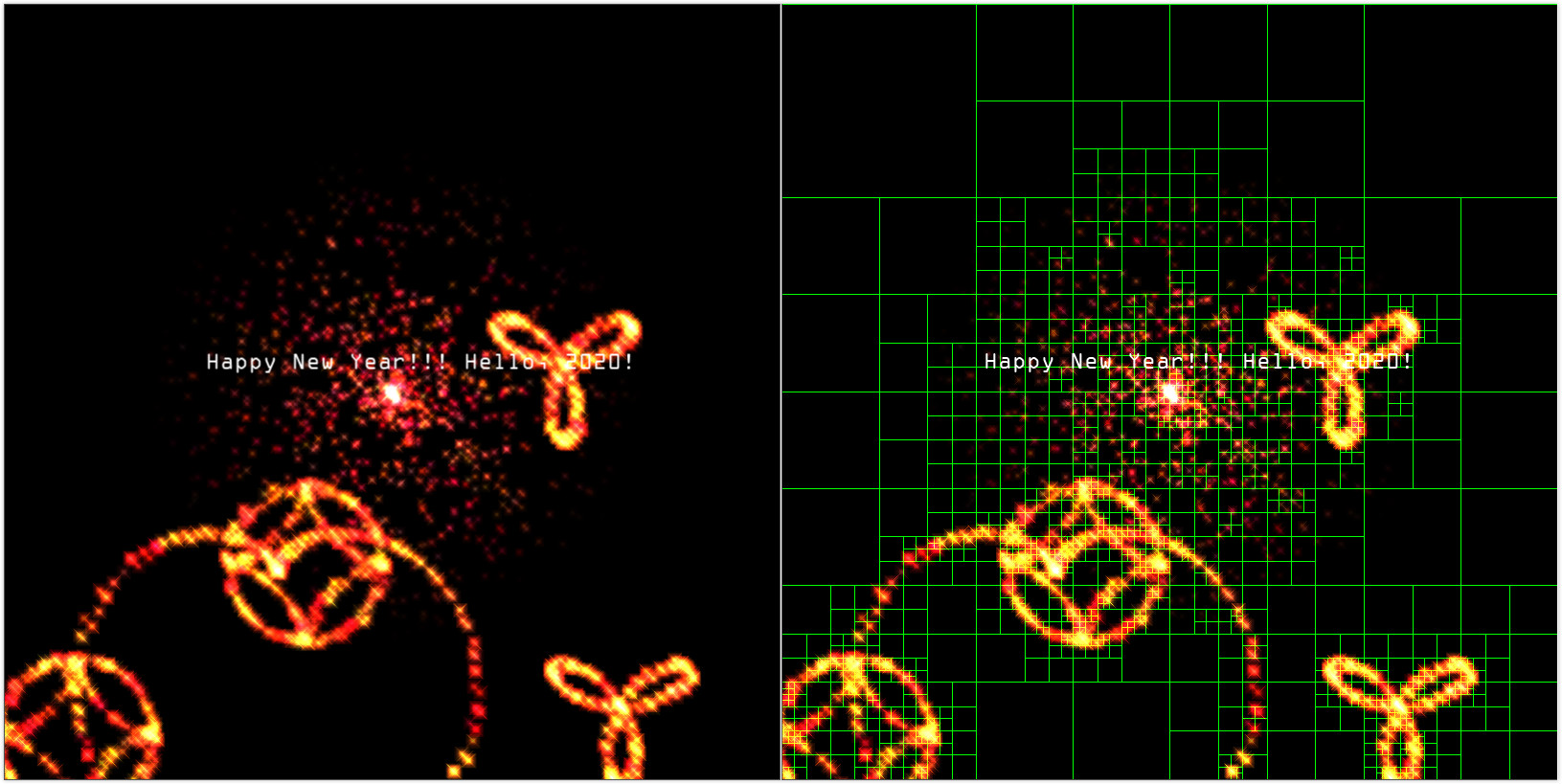
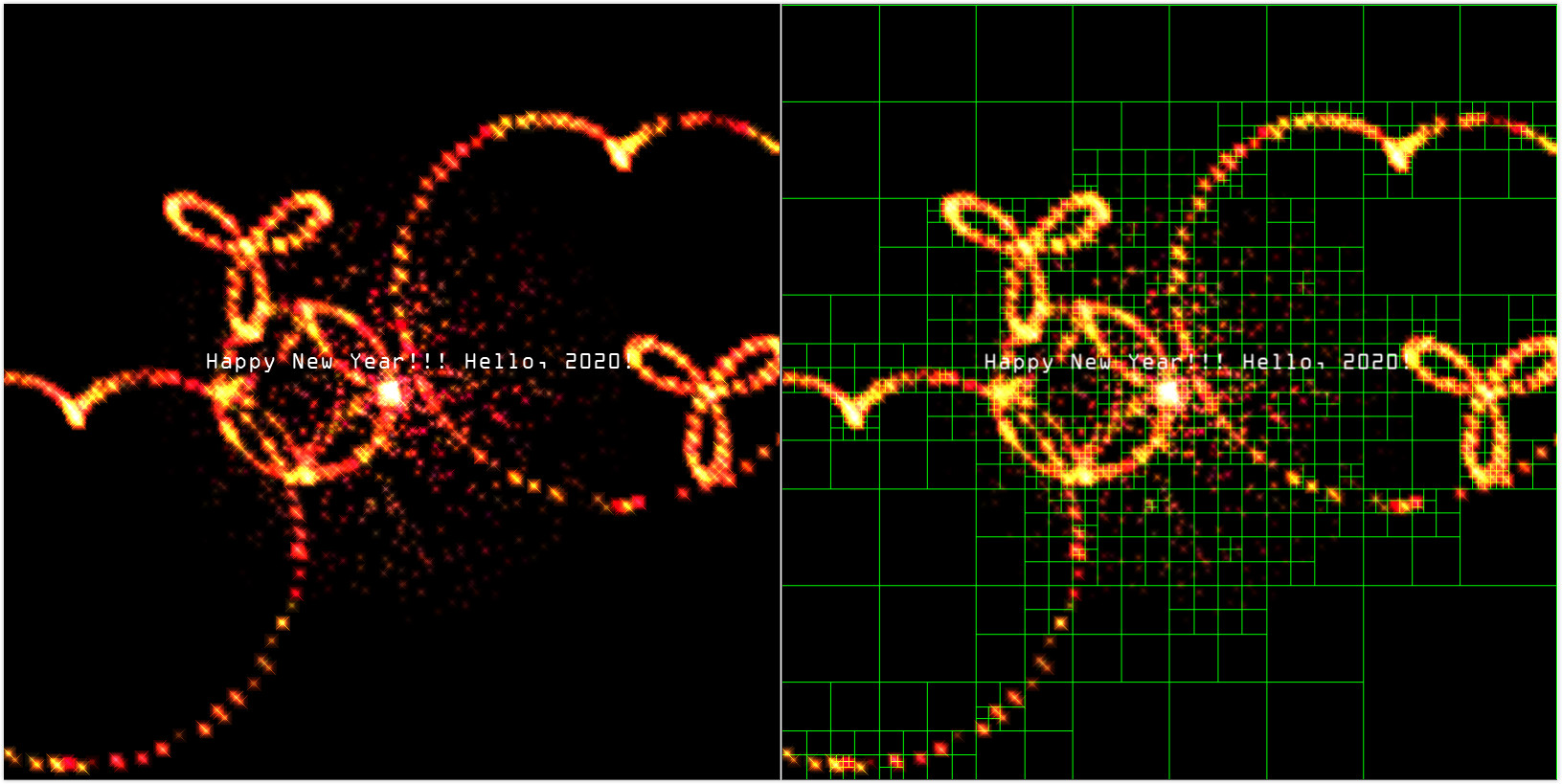
 关于四叉树的可视化部分就到这里,下面来看看三维八叉树在计算机图形学光线追踪渲染技术中的实际应用和性能提升。
## 三、利用八叉树算法加速射线求交
四叉树和八叉树从本质上来讲没有区别,算法的思想都是一样的,只不过四叉树是针对二维的情况,而八叉树针对的是三维的情况。在三维空间均匀划分的是一个长方体,每一个长方体分割成八个相同的子长方体,因而三维情况的空间分割树有八个子节点,被称为八叉树。Wiki的八叉树定义为: 八叉树(Octree)是一种用于描述三维空间的树状数据结构。八叉树的每个节点表示一个正方体的体积元素,每个节点有八个子节点,这八个子节点所表示的体积元素加在一起就等于父节点的体积。一般中心点作为节点的分叉中心。
关于四叉树的可视化部分就到这里,下面来看看三维八叉树在计算机图形学光线追踪渲染技术中的实际应用和性能提升。
## 三、利用八叉树算法加速射线求交
四叉树和八叉树从本质上来讲没有区别,算法的思想都是一样的,只不过四叉树是针对二维的情况,而八叉树针对的是三维的情况。在三维空间均匀划分的是一个长方体,每一个长方体分割成八个相同的子长方体,因而三维情况的空间分割树有八个子节点,被称为八叉树。Wiki的八叉树定义为: 八叉树(Octree)是一种用于描述三维空间的树状数据结构。八叉树的每个节点表示一个正方体的体积元素,每个节点有八个子节点,这八个子节点所表示的体积元素加在一起就等于父节点的体积。一般中心点作为节点的分叉中心。
想象一个立方体,我们最少可以切成多少个相同等分的小立方体?答案就是8个。再想象 我们有一个房间,房间里某个角落藏着一枚金币,我们想很快的把金币找出来。 我们可以把房间当成一个立方体,先切成八个小立方体,然后排除掉没有放任何东西的小立方体,再把有可能藏金币的小立方体继续切八等份…. 如此下去,平均在$Log_8$(房间内的所有物品数)的时间内就可找到金币。八叉树就是用在3D空间中的场景管理,可以加速我们的物体搜索、碰撞检测、射线求交、邻域搜索等等空间查找操作。
一般情况下,八叉树的构建过程如下:
- (1).设定最大递归深度;
- (2).找出场景的最大尺寸,并以此尺寸建立第一个立方体;
- (3).依序将单位元元素丢入能被包含且没有子节点的立方体;
- (4).若没有达到最大递归深度,就进行细分八等份,再将该立方体所装的单位元元素全部分担给八个子立方体;
- (5).若发现子立方体所分配到的单位元元素数量不为零且跟父立方体是一样的,则该子立方体停止细分,因为跟据空间分割理论,细分的空间所得到的分配必定较少,若是一样数目,则再怎么切数目还是一样,会造成无穷切割的情形;
- (6).重复步骤(3),直到达到最大递归深度。
光线追踪是一个递归的过程。发射一束光线到场景,求出光线和几何图形间最近的交点,如果该交点的材质是反射性或折射性的,可以在该交点向反射方向或折射方向继续追踪,如此递归下去,直到设定的最大递归深度或者射线追踪到光源处(或者背景色),如此便计算处一个像素的着色值。光线追踪算法涉及到大量的光线与几何体的求交点运算,因而与渲染效率息息相关。复杂物体大多采用三角形网格表示,因而进一步来说是射线与三角形的求交运算。下面我将为每个三角网格模型构建一颗八叉树,加速射线与三角网格模型的求交。
1、八叉树分割算法——构建与销毁
在开始构建之前,我们首先要弄清楚一点的就是在这里数据对象是一个个三角形而非一个个点,三角形是由一定的大小的,它有可能刚好处在分割平面上,导致三角形跨越了多个子节点。这时为了防止遗漏,应该把三角形都存储到由交集的节点中。同时,每个叶子节点中并不会直接存储三角形图元数据,而是存储三角形面片的索引。定义八叉树节点如下所示:
1 | struct Node |
上面的$m_objectIds$s是一个三元组的vector,三元组的每个元素存储一个三角形面片的三个顶点索引。然后输入模型的三角形面片列表,我们自顶向下构建八叉树。构建的过程其实跟四叉树的构建过程差别不大,区别在于子区域的划分:
1 | Node *Octree::recursiveBuild(unsigned int depth, Vector3D min, Vector3D max, |
构建过程的时间复杂度为$Nlog_8\ N$。同样的,八叉树销毁过程采用后序遍历的方式:
1 | void Octree::recursiveDestory(Node * node) |
这里有一点需要特别注意的就是需要判断一个立方体区域是否与三角形相交或包含,我采用的方法是首先判断三角形的三个点中是否至少有一个在立方体内部,如果是则返回真。而如果三角形的三个顶点均不在立方体区域内部,但仍有可能三角形与立方体区域存在交集,此时可以通过依次判断三角形的三条边是否与立方体相交。
1 | bool Octree::isContain(const AABB & box, const Vector3D & p1, const Vector3D & p2, const Vector3D & p3) |
2、八叉树分割算法——访问
构建了八叉树之后,八叉树的优势就体现出来了,在光线追踪过程每发射一条射线我们就要检测该射线与场景中的物体是否发生了碰撞,如果发生了碰撞则需要将碰撞的点计算出来。有了八叉树结构,我们首先检测射线是否与当前节点的区域发生了碰撞,如果不发生碰撞则直接退出;而如果发生了碰撞且当前节点是叶子节点的话,则遍历叶子节点存储的三角形,计算射线与三角形的交点,取距离射线源最近的结果;而当前节点是内部节点的话,则递归调用遍历程序,判断射线是否与该区域的八个子区域碰撞,有碰撞才会继续往下走,无碰撞则不会往下深入。
这个算法的实现并不复杂,实现代码如下:
1 | bool Octree::recursiveTraveling(Node * node, const Ray & ray, float & t_min, float & t_max, |
可以看到,通过八叉树的结构我们可以避免很多无用功,大大加速整个求交的过程,有了八叉树后射线与三角形求交的时间复杂度就变成了$O(log_8 N)$,其中$N$是输入规模,相比于原来的$O(N)$复杂度提升非常明显。下面就通过实验比较有无八叉树的算法效率。至于光线追踪方面的算法,与本门课的主题关系比较小,而且涉及的内容实在太多,因此不再赘述。
3、八叉树加速实验结果
我们将对比两个场景渲染的实验,两个场中均涉及到复杂的三角网格模型。控制的变量有每个像素发射的采样光线个数、有无八叉树加速。一般情况下,采样光线数量越多越好,数量过少会导致渲染出来的图片噪声过多,质量太低。场景中三角网格比较多的模型如下图5所示:



下面的表1给出了两个场景在有无八叉树时的渲染时间对比,表格中的s是second的缩写,即单位为秒。表格的最后一列有两个“>3小时“是因为等不下去了,就不再等了,花费的时间实在太长了。通过表格可以看到,有了八叉树的加速,时间效率提升极其明显,特别是采样数量越多的时候,提升倍数越多,完全是几个数量级的提升。这是因为采样数量呈指数增值时,射线与三角形的求交数量也呈指数增长。
| scene | 16次采样 | 64次采样 | 128次采样 | 512次采样 |
|---|---|---|---|---|
| dragonSquare(无八叉树) | 427.776s | 2195.918s | 8715.48s | >3小时 |
| dragonSquare(有八叉树) | 17.824s | 70.382s | 147.72s | 614.562s |
| dragonBox(无八叉树) | 380.944s | 1818.491s | 6548.502 | >3小时 |
| dragonBox(有八叉树) | 13.136s | 58.661s | 105.642s | 422.652s |
四、总结
分治算法思想是一个非常有用的算法思想,我们围绕分治算法这一主题展开其在计算机图形学中应用——四叉树和八叉树空间分割算法实践。抛开诸多细节不说,四叉树和八叉树在本质上与二分查找类似。与二分查找的排序预处理一样,四叉树和八叉树都需要在最开始构建,构建的复杂度与排序的时间复杂度一致,对于那些查找密集型的应用场景来说非常划算(提升的效率极其恐怖)。当然,四叉树和八叉树并不完美的,它们也有缺点,一个比较大的缺点就是它要求空间物体对象分布比较均匀,如果分布不均匀,那么构建出来的树将不会很平衡,这将影响后续的访问效率。针对这一问题,后续的学者已经有比较多的算法变种,限于篇幅这里不再详细展开。



