在基于粒子的流体模拟中,Marching Cubes$^{[1]}$是常用的、流行的表面重建算法。但在Marching Cubes算法构建表面网格之前需要获得整个流体区域的标量场,这个标量场需要我们根据流体的粒子计算得到,这个标量场的质量好坏与最终重建得到的网格质量好坏息息相关。针对采用Marching Cubes算法重建粒子流体表面网格的方法,学者们都着重关注如何提高重建出来的流体网格质量、如何提高表面重建过程的时间效率和内存效率,因此我们从表面网格质量、重建算法效率两方面着手基于粒子的流体表面重建的综述。
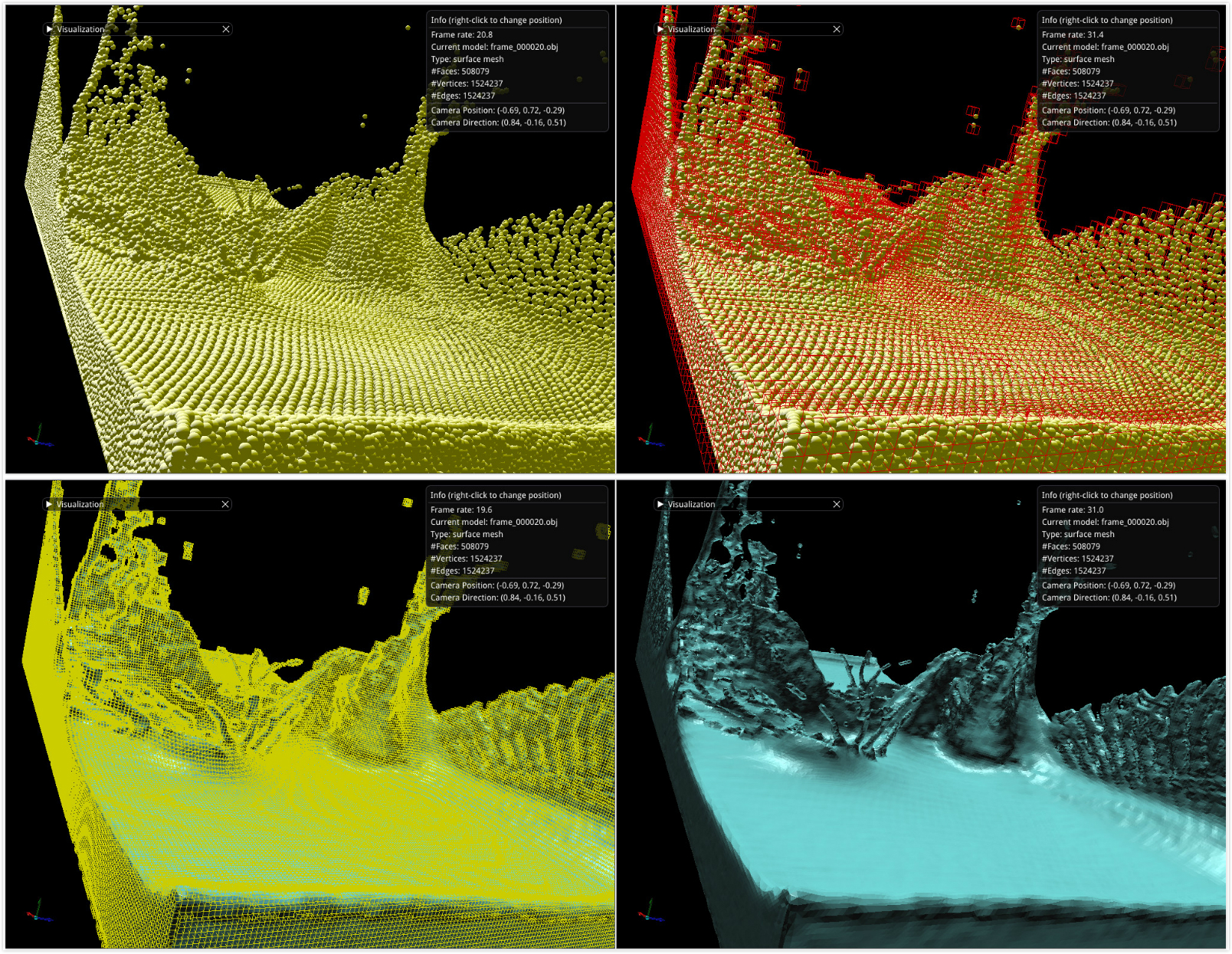
在基于粒子的流体模拟中,Marching Cubes$^{[1]}$是常用的、流行的表面重建算法。但在Marching Cubes算法构建表面网格之前需要获得整个流体区域的标量场,这个标量场需要我们根据流体的粒子计算得到,这个标量场的质量好坏与最终重建得到的网格质量好坏息息相关。针对采用Marching Cubes算法重建粒子流体表面网格的方法,学者们都着重关注如何提高重建出来的流体网格质量、如何提高表面重建过程的时间效率和内存效率,因此我们从表面网格质量、重建算法效率两方面着手基于粒子的流体表面重建的综述。
一、表面网格质量
表面网格的质量主要取决于标量场,因为表面网格本质上是从标量场提取出来的,标量场的好坏对表面网格的质量影响重大。这里标量场就是符号距离场,它隐式地表示了流体表面网格,我们必须从这个标量场获取显式的三角形网格用以后续的渲染。为了提高重建出来的表面网格质量,一方面我们可以提高标量场网格的分辨率,随着分辨率的提高我们重建出来的网格能够更多地捕获流体细节,网格更加细致,但随之而来的代价就是庞大的计算量和内存开销;另一方面就是从流体表面的标量场定义函数入手,因为粒子凹凸不平的原因,如果表面函数定义得不好,那么很难重建出平滑、自然的表面网格。
针对表面定义函数这一部分,已有不少学者提出了不同的表面函数。
1、Blinn
Blinn等人最早提出了一种表面定义函数$^{[2]}$,其数学定义为:
上式计算了某一点$(x,y,z)$的密度值,然后表面就被定义为密度值等于某个阈值$T$的等值面:
该方法计算简单,缺点就是不能够产生平滑的表面网格,尤其对于那些具有尖锐特征的流体粒子。
2、Müller
接着Müller等人提出了采用周围邻域粒子的加权叠加来计算标量场的值$^{[3]}$,标量场的值依旧是密度值减去给定的阈值,密度值计算采用下面的公式:
其中,$r$是标量场中的要计算标量值的一点,$h$是光滑核半径,$W$是权重函数。这种计算标量场的方法虽然在一定程度上优于了Blin$^{[2]}$等人提出的方法,但重建出来的网格依旧不够平滑。
3、Zhu and Bridson
为了进一步提升平滑性,Zhu和Bridson等人提出了采用粒子的符号距离场来定义流体的表面标量场$^{[4]}$,其数学定义如下所示:
其中的$\Phi(x)$就是流体的标量场函数,$\overline x$和$\overline r$是平均位置和平均半径。该方法构建出来的网格已经很平滑了,但是有个致命的缺点,那就是在高曲率的地方质心容易被甩出流体区域,造成了失真。
4、Adams
Adams等人采用了一种完全不同的策略来重建流体表面$^{[5]}$,他们提出在模拟初始时为每个粒子计算其到表面的距离并保存,在后续的模拟过程中更新这个距离(redistancing)。给定每个粒子$i$的到表面的距离$d_i$,流体表面就定义为下面水平集函数$\phi(x)$的零等值面:
其中的$w_i(x)$是光滑的对称权重函数。该方法采用了新奇的思路来重建流体表面,与Zhu Bridson等人的方法相比,能够重建出更加平滑的流体表面,但算法比较复杂,计算量也比较大,更适用于自适应采样的粒子流体模拟方法。
5、Solenthaler
针对Zhu Bridson等人的缺点,Solenthaler等人在他们的基础上做了改进$^{[6]}$。Solenthaler等人将前面的公式$(4)$改成如下的形式:
与原来的公式相比,多了一个因子$f$,其计算公式如下:
其中的$t_{high}$和$t_{low}$分别是设定的参数,取值分别为$3.5$和$0.4$。而公式$(7)$中的$EV_{max}$是$3\times 3$雅可比矩阵$\nabla_x(\overline x(x))$的最大特征值。这种方法考虑了高曲率区域质心被甩出流体外的情况,显著改善了Zhu Bridson等人的方法存在的缺点。
6、Yu and Turk
目前效果最好的方法当属Yu和Turk等人提出的基于各向异性核的粒子流体表面重建方法$^{[7]}$。他们利用了加权主成分分析法,为了每个流体粒子计算一个协方差矩阵$C_{i}$并对其做奇异值分解,根据得到的特征值和特征向量计算变换矩阵$G_i$。最后通过这个变换矩阵将原本球形的光滑核变换成有偏向性的椭球形。
对协方差矩阵$C_i$做奇异值分解(简称SVD),得到特征值和特征向量:
每个粒子的各向异性变换矩阵$G_i$就为:
最后标量场的计算公式如下:
在标量场计算之前他们还对流体粒子做了一个拉普拉斯平滑处理,使得流体粒子整体上向内部收缩了一些。可以看到,该方法计算量极大,相比先前的方法多了不少数学运算,但不得不说目前这种方法重建出来的表面网格质量最佳。
总的来说,由于表面函数与重建网格的质量关系密切,因此不少学者围绕这方面的问题做了不少的研究,目前最好的方法已经可以重建出来质量极高的表面网格了,但高质量的方法普遍的缺点就是计算量大,算法相比之下实现起来也比较复杂。因此,如何在保证质量的前提下减少算法的计算量或许是个值得探究的课题。
二、重建算法效率
表面重建这一步介于流体模拟和流体渲染之间,是尤为重要的一步,与后续的渲染质量息息相关。但是由于表面重建过程不仅涉及到MC三角化,还涉及到标量场的计算,其中标量场的计算是整个重建过程最为耗时的部分。目前已有不少学者围绕重建效率展开相关的研究,提出了一些高速并行的高效算法。
1、Müller
Müller等人早之前已经提出了窄带的思想$^{[3]}$,他们指出可以先找出在流体表面区域附近的标量场格子,然后仅仅在这些格子上执行Marching Cubes算法。然而Müller等人只是顺带一提,并没有给出具体的解决可能存在的”双层“问题和可行的并行方案。
2、Bridson
针对传统八叉树的效率问题,Bridson提出了一种稀疏块网格结构$^{[8]}$,只有在窄带区域这些块才存在并可以细分成更加精细的均匀网格。他们的方法本质上就是采用了两重不同分辨率的空间网格,先用较为粗糙的稀疏网格找出窄带区域,然后在窄带区域做进一步的细分,以此大大节省了内存空间占用。
3、Houston
Houston等人设计了一种新颖的稀疏水平集结构$^{[9]}$,他们的方法采用了游程编码(run-length encoding),根据到窄带区域的距离对流体区域进行编码,可扩展性强。算法效率有所提升,但很难设计成高速并行的程序结构。
4、Nielsen
Nielsen等人提出了一种动态管网的网格数据结构(DT-grid)$^{[10]}$,与八叉树不同,这种结构是非层次的,能够大大提升内存效率。之后为了提高高分辨率下的效率,Nielsen等人又提出了一种不同的结合了压缩策略的技术$^{[11]}$。同样地,他们的方法都难以高速并行化,因为这些方法被设计出来时就没有考虑过并行。
5、Akinci
注意到先前的方法在高速并行化方面做的工作较少,Akinci等人开始着手重建过程的GPU并行化工作,围绕基于窄带的表面重建这个主题,他们设计了一种高速并行化的表面重建管线$^{[12]}$,整个管线大致分成两个阶段,分别是标量场的计算和MC三角化。相比之前串行的方法,他们的算法获得非常高的加速比,但是整个重建过程并没有被完全并行化,为了避免可能潜在的线程竞争有一些阶段还是需要串行执行。此外,他们的表面粒子提取方法不是很好。
6、Wu
继Akinci等人之后,Wu等人针对Akinci等人方法的内存效率问题做了一些改进$^{[13]}$,他们利用一种并行高效的布谷鸟哈希表替换原本的均匀网格,从而减少无用的内存空间耗费,提升了内存效率。但在并行管线上与原来相比并没有太大的改变,依旧没有实现完全并行化。
7、Kanai
在追求高速并行化的同时,也有研究者研究如何减少重建出来网格的三角形数量,这是因为在一些平坦的区域我们没有必要生成那么多的三角形,在曲率比较高的区域可以生成更多的三角形以捕获更多的细节。但是由于我们目前采用的方案都是均匀的空间网格,因此无论是平坦区域还是复杂区域我们都生成了同样数量的三角形。Kanai 等人综合考虑了并行化和自适应网格,他们将Akinci等人提出的三层网格自适应表面重建的方案$^{[15]}$进行了并行化,并针对不同分辨率的网格之间存在的裂缝问题进行了修补$^{[14]}$。但该方法因为需要考虑如何进行修补裂缝,算法比较复杂,并行方案相对于基于窄带的并行算法速度要慢一些。
总的来说,目前GPU并行化还存在一些问题。基于窄带的方案应该是目前最佳的,但是受限于一些潜在的竞争条件不能完全地将整个过程并行化,表面窄带的构建算法也值得探讨是否能够重新调整一下。
参考文献
$[1]$ Lorensen W E, Cline H E. Marching cubes: A high resolution 3D surface construction algorithm[C]//ACM siggraph computer graphics. ACM, 1987, 21(4): 163-169.
$[2]$ Blinn J F. A generalization of algebraic surface drawing[J]. ACM transactions on graphics (TOG), 1982, 1(3): 235-256.
$[3]$ Müller M, Charypar D, Gross M. Particle-based fluid simulation for interactive applications[C]//Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation. Eurographics Association, 2003: 154-159.
$[4]$ Zhu Y, Bridson R. Animating sand as a fluid[J]. ACM Transactions on Graphics (TOG), 2005, 24(3): 965-972.
$[5]$ Adams B, Pauly M, Keiser R, et al. Adaptively sampled particle fluids[C]//ACM Transactions on Graphics (TOG). Acm, 2007, 26(3): 48.
$[6]$ Solenthaler B, Schläfli J, Pajarola R. A unified particle model for fluid–solid interactions[J]. Computer Animation and Virtual Worlds, 2007, 18(1): 69-82.
$[7]$ Yu J, Turk G. Reconstructing surfaces of particle-based fluids using anisotropic kernels[J]. ACM Transactions on Graphics (TOG), 2013, 32(1): 5.
$[8]$ Bridson R E, Fedkiw R. Computational aspects of dynamic surfaces[D]. stanford university, 2003.
$[9]$ Houston B, Wiebe M, Batty C. RLE sparse level sets[C]//ACM SIGGRAPH 2004 Sketches. ACM, 2004: 137.
$[10]$ Nielsen M B, Museth K. Dynamic Tubular Grid: An efficient data structure and algorithms for high resolution level sets[J]. Journal of Scientific Computing, 2006, 26(3): 261-299.
$[11]$ Nielsen M B, Nilsson O, Söderström A, et al. Out-of-core and compressed level set methods[J]. ACM Transactions on Graphics (TOG), 2007, 26(4): 16.
$[12]$ Akinci G, Ihmsen M, Akinci N, et al. Parallel surface reconstruction for particle‐based fluids[C]//Computer Graphics Forum. Oxford, UK: Blackwell Publishing Ltd, 2012, 31(6): 1797-1809.
$[13]$ Wu W, Li H, Su T, et al. GPU-accelerated SPH fluids surface reconstruction using two-level spatial uniform grids[J]. The Visual Computer, 2017, 33(11): 1429-1442.
$[14]$ Du S, Kanai T. Gpu-based adaptive surface reconstruction for real-time sph fluids[J]. 2014.
$[15]$ Akinci G, Akinci N, Oswald E, et al. Adaptive surface reconstruction for SPH using 3-level uniform grids[J]. 2013.



