研一上学期课程比较繁重,加上在实验室要做的事情也多,所以最近博客都没更新了。最近数图课上到频域变换处理相关章节,其中的傅里叶变换其实在图形学领域也有颇多的应用(例如大规模的海水模拟),遂写下这篇博客整理了一些关于傅里叶变换的内容。
傅里叶变换在高等数学中早有涉及,只不过当时叫傅里叶级数 ,即给定一个连续函数,我们可以将其展开成一系列不同系数的正弦函数和余弦函数的叠加(与泰勒级数具有相似的形式)。傅里叶变换涉及到了的复数域,我们先来看一些复数域的内容。
一、复数域 复数的内容在高中已经学过,这里只是将一些复数域的定义和性质罗列出来。复数$C$的定义如下:
其中$R$和$I$均为实数,$j$是$-1$的平方根,即$j=\sqrt{-1}$或者说$j^2=-1$。$R$是复数的实部,$I$是复数的虚部。因此实数域是虚部$I=0$的复数域子集。给定复数$C$,其共轭的定义$C’$为:
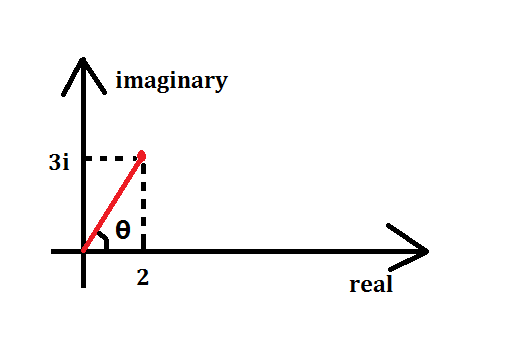
复数的实部$R$和虚部$I$可以看成复平面 上的一个二维点$(R,I)$,该复平面的横坐标是实数轴,纵坐标是虚数轴,如下图1所示。因此复数$R+jI$等价于复平面直角坐标系中的点$(R,I)$。
图1 复平面直角坐标系
定义复数的模就是在复平面上的复数点到原点的距离$|C|=\sqrt{R^2+I^2}$。$\theta$是点向量与实数轴的夹角,因此$\tan\theta=\frac IR$,在已知$I$和$R$的情况下,可以计算$\theta=arctan(I/R)$。有了模长和夹角,我们可以将其复数域从直角坐标系转成极坐标系下的形式:
上式等价于公式$(1)$,因为$|C|cos\theta=R$、$|C|sin\theta=I$。又有欧拉公式$e^{j\theta}=cos\theta+jsin\theta$,因此可以将公式$(3)$用欧拉公式替换成如下形式:
复数的四则运算与实数类似,我们牢牢记住$j^2=-1$即可。这里只看复数的加法和乘法,给定两个复数$C_1=a+jbj$和$C_2=c+jd$,则其相加和相乘的结果为:
复数与实数运算更加简单,直接实数与实部运算、实数与复部运算即可。傅里叶变换要用到的复数域性质就这些,我们可以定义实现一个简单的复数类,将上面的求模、取共轭、四则运算实现,方便后面的傅里叶变换。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 class Complex { public : Complex() : real(0.0 ), imaginary(0.0 ) {} Complex(double r, double i = 0.0 ) : real(r), imaginary(i) {} Complex(const Complex &other) { real = other.real; imaginary = other.imaginary; } Complex operator +(const Complex &other) const ; Complex operator -(const Complex &other) const ; Complex operator *(const Complex &other) const ; Complex operator *(const double &value) const ; Complex &operator +=(const Complex &other); Complex &operator -=(const Complex &other); Complex &operator *=(const Complex &other); Complex &operator *=(const double &value); Complex conjugate () const ; double length () const double getReal () const return real; } double getImaginary () const return imaginary; } void setReal (const double &value) void setImaginary (const double &value) private : double real; double imaginary; }; Complex Complex::operator +(const Complex & other) const { return Complex(this ->real + other.real, this ->imaginary + other.imaginary); } Complex Complex::operator -(const Complex & other) const { return Complex(this ->real - other.real, this ->imaginary - other.imaginary); } Complex Complex::operator *(const Complex & other) const { return Complex( this ->real * other.real - this ->imaginary * other.imaginary, this ->real * other.imaginary + this ->imaginary * other.real); } Complex Complex::operator *(const double & value) const { return Complex(this ->real * value, this ->imaginary * value); } Complex & Complex::operator +=(const Complex & other) { this ->real += other.real; this ->imaginary += other.imaginary; return *this ; } Complex & Complex::operator -=(const Complex & other) { this ->real -= other.real; this ->imaginary -= other.imaginary; return *this ; } Complex & Complex::operator *=(const Complex & other) { *this = (*this ) * other; return *this ; } Complex & Complex::operator *=(const double & value) { *this = (*this ) * value; return *this ; } Complex Complex::conjugate() const { return Complex(this ->real, -this ->imaginary); } double Complex::length() const { return sqrt (this ->real * this ->real + this ->imaginary * this ->imaginary); }
二、傅里叶变换 接下来就是傅里叶变换的一些基本内容,包含连续域的傅里叶变换和离散域的傅里叶变换形式。
1、傅里叶级数 首先来回顾一下高数中的傅里叶级数。给定一个具有周期$T$的连续变量$t$的周期函数$f(t)$,该函数可以被展开成一系列适当系数的正弦和余弦的系数加权和,具体形式如下:
$c_n$则是相应的权重系数,它被称为傅里叶系数,是一个具体的值而非函数,它的具体计算公式如下:
根据欧拉公式$e^{j\theta}=cos\theta+jsin\theta$,其中$e^{j\frac{2\pi n}{T}t}=cos(\frac{2\pi n}{T}t)+jsin(\frac{2\pi n}{T}t)$。因此公式$(6)$可以写成包含正弦和余弦函数的形式:
公式$(8)$的意思就是$f(t)$可以展开成$n$个正弦和余弦的叠加。设三角函数的通式为$Asin(\omega x+q)。$对于每一个$n$,都对应一个振幅为$A=c_n$、周期为$\frac{2\pi}{\omega}=\frac{2\pi}{\frac{2\pi n}{T}}=\frac Tn$、频率为$n/T$的正弦和余弦,这些正弦和余弦是$f(t)$的一个分量。因此所有($n$个)不同振幅、不同周期、不同频率的正弦和余弦构成了最初原来的那个函数$f(t)$。
图2 不同振幅、不同频率的波
一个恰当的比喻就是将傅里叶变换比作一个玻璃棱镜。棱镜是可以将光分成不同颜色成分的物理仪器,每个成分的颜色由波长(或频率)决定。傅里叶变换可以看作是“数学的棱镜”,将函数基于频率分成不同的成分。当我们考虑光时,主要讨论它的光谱和频率谱线。同样,傅里叶变换使我们能够通过频率成分来分析一个函数。
2、连续变量的傅里叶变换 连续变量$t$的连续函数$f(t)$的傅里叶变换由下式定义:
公式$(9)$其实对应于前面的公式$(7)$,即求傅里叶展开中的傅里叶系数,用$F(\mu)$表示,$\mu$也是一个连续变量(对应前面的$n/T$)。用欧拉公式可以把公式$(9)$表示为:
即便$f(t)$是实数,其傅里叶变换得到的系数通常是复数。变量$\mu$决定了相应的正弦波、余弦波的频率,因此傅里叶变换域是频率域。公式$(9)$是傅里叶正变换,即将时空域的值变换到频率域。同样地,我们可以将其变换回来(因为傅里叶变换是可逆的),这就是傅里叶反变换,其数学形式如下(对应前面的公式$(6)$):
可以看到,傅里叶正变换和反变换非常类似,在形式上仅在一些符号以及系数上有点差别。傅里叶的正变换即公式$(9)$和傅里叶反变换即公式$(11)$构成了傅里叶变换对 。在应用领域通常正变换和反变换都需要用到。目前讨论的都是一元函数,进一步地我们可以把它扩展到二元函数,二维的连续傅里叶变换对由以下两个表达式给出:
其中的$u$、$v$是频率变量。
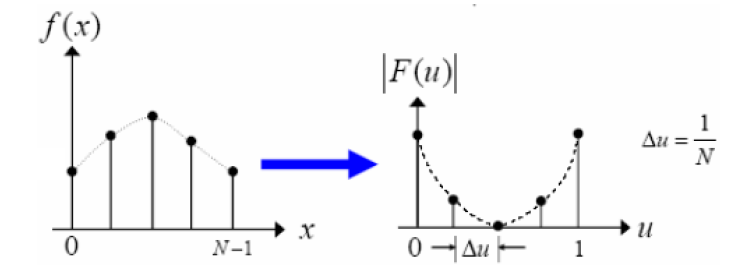
3、离散形式的傅里叶变换 在现实的工程实现中,通常我们只能对连续函数$f(t)$进行一个离散的采样,得到离散的$f(t)$值(如下图3左边所示)。我们的图像就是对真实光照的离散采样,每一个像素对应一个采样点,像素值就是采样得到的函数值。相应地,我们将在这些离散采样的点上进行傅里叶变换,得到相应的傅里叶系数。
图3 离散傅里叶变换
由于$f(t)$是一个周期函数,因此通常只需采样一个周期的样本即可。对于一个$M\times N$大小的二维图像,它可以看成周期为$M\times N$的离散采样。设$x=0,1,2,3,…,N-1$是采样点,采样间隔为$\Delta x$,相应的$f(x)$是采样得到的离散信号,则其离散傅里叶正变换和反变换换定义如下:
离散傅里叶变换就是把积分符号换成了累加符号,同时积分区间换成了一个周期(这里一个周期就是$N$)。注意傅里叶变换后得到的函数是在复数域内的,即$F(\mu)=R(\mu)+jI(\mu)=|F(\mu)|e^{j\phi(\mu)}$。下面是关于傅里叶变换的基本概念,这些概念在前面复数域已经提到过了,只不过换了一个名字。
傅里叶谱 :$|F(\mu)|=[R^2(\mu)+I^2(\mu)]^{1/2}$,就是傅里叶系数的模长(因为变换得到的是复数)。相角 :$\phi(\mu)=arctan(\frac{I(\mu)}{R(\mu)})$,就是复平面上的$\theta$角。能量谱 :$P(\mu)=|F(\mu)|^2=R^2(\mu)+I^2(\mu)$,模长的平方。
离散的傅里叶变换后的函数$F(\mu)$也是离散的,其采样的点分布在$u=0,\Delta \mu,2\Delta \mu, …,(N-1)\Delta \mu$,$\Delta x$和$\Delta \mu$有如下的反比关系:
同样地,推广到二维。二维离散傅里叶变换本质上是一维情况向两个方向的简单扩展:
这里可以发现一个非常有趣的地方,当$\mu = 0,v=0$时,傅里叶变换得到的本质上就是原离散函数的均值:
4、傅里叶变换的性质 傅里叶变换有许多非常有用的性质,这里只记录一些关键和重要的性质。
周期性 :正变换和反变换均有的性质,$F(\mu,v)=F(\mu + M,v)=F(u,v+N)=F(\mu+M,v+N)$,$f(x,y)=f(x+M,y)=f(x,y+N)=f(x+M,y+N)$,可以看到这里$f(x,y)$也是有周期性的。具体到二维的图像处理就是我们将一张图像重复地平铺(像贴地板瓷块一样),所以在$x$和$y$方向上的周期就是图像的宽和高。周期性不难理解,具体证明也不难。共轭对称性 :若$f(x,y)$时实函数,则$F(\mu,v)=F’(-\mu,-v)$,$|F(\mu,v)|=|F’(-\mu,-v)|$。注意这里必须要求时$f(x,y)$是实函数,否则将是共轭反对称性。平移性 :空间域的平移,$f(x-x_0,y-y_0)\iff F(\mu,v)e^{-j2\pi (\mu_0x/M+v_0y/N)}$;频率域的平移,$f(x,y)e^{j2\pi(\mu_0x/M+v_0y/N)}\iff F(\mu-\mu_0,v-v_0)$。这个性质告诉我们,在一个领域的平移等价于另一个领域的函数值乘上一个指数系数。在图像处理中,频率域的平移很常用,当$\mu_0=M/2,v_0=N/2$时,$e^{j2\pi(\mu_0x/M+v_0y/N)}=(-1)^{x+y}$,将频率域的原点平移到了图像的中心点$(M/2,N/2)$。
5、图像频率域的滤波步骤 图像频率域的滤波和空间域的滤波有一一对应的关系。二维卷积定理 表明,在空间域的循环卷积滤波等价于频率域的点乘:
上式中,$f(x,y)$就是待滤波的图像,$h(x,y)$是卷积核,相应的$F(\mu,v)$是由$f(x,y)$做傅里叶正变换得到的,$H(\mu,v)$是由卷积核$h(x,y)$做傅里叶变换得到的。$H(\mu,v)$和$F(\mu,v)$做点乘并不是向量的点乘,它们都是一个二维的矩阵,所谓的点乘就是两个矩阵中相同位置的元素相乘,得到的结果依旧是一个矩阵,记为$G(\mu,v)=F(\mu,v)H(\mu,v)$。最后将$G(\mu,v)$通过傅里叶反变换就得到了滤波后的图像,记为$g(x,y)$。
因此,二维的图像频率域滤波步骤如下:
将原图像的像素值$f(x,y)$乘上$(-1)^{x+y}$,得到$f(x,y)(-1)^{x+y}$,由平移性可知,这一步相当于将频率域的原点平移到了图像的中心点$(M/2,N/2)$;
将$f(x,y)(-1)^{x+y}$做傅里叶正变换,得到$F(\mu-M/2,v-N/2)$,注意不是$F(\mu,v)$;
在频率域执行点乘,得到滤波后的矩阵$G(\mu-M/2,v-N/2)=H(\mu- M/2,v-N/2)F(\mu-M/2,v-N/2)$;
对$G(\mu-M/2,v-N/2)$执行傅里叶反变换,得到$g(x,y)(-1)^{x+y}$;
最后将$g(x,y)(-1)^{x+y}$再乘上$(-1)^{x+y}$得到$g(x,y)$,即滤波后的图像。
滤波矩阵$H$并不一定要通过空间域的卷积核做傅里叶正变换得到,可以直接在频率域设计相关的滤波器。这里略提一下傅里叶变换得到的频谱图与空间域原图的联系,傅里叶变换得到的频谱图显示的每个正弦波的振幅,振幅越大则代表对应频率的正弦波在原函数中的成分占比越多 。经过中心化之后,在图像中心的是低频正弦波的振幅,从中心向四周频率越高,相应的四周频谱值代表高频正弦波的振幅。低频成分代表了变化较为缓慢的部分,相应的就是在空间域的图像比较平滑的部分;高频成分代表了变化剧烈的部分,相应的就是在空间域的图像灰度值变化比较迅速的部分(例如边缘)。频谱的$uv$坐标并不和空间域的图像$xy$坐标一一对应,因而相应的值也不是一一对应的。频谱$(u,v)$处的值取决于空间域图像的所有像素值,是一个从空间域到频率域的多对一 的映射关系,坐标$(u,v)$蕴含了平面波的频率和角度,因而坐标$(u,v)$和该坐标处的频谱值能够代表一个平面波(当然这个平面波还不包含相位信息,这个相位信息蕴含在相角当中)。
三、傅里叶变换的实现 上面讨论了一些关于傅里叶变换的理论内容,接下就是关于傅里叶变换的具体实现。我们把目光放到下面的二维离散傅里叶变换公式:
其中的$\mu$取值范围为$0,1,…,M-1$,$v$的取值范围为$0,1,…,N-1$。$M$和$N$是图像的宽度和高度。因此$F(\mu,v)$是一个$M\times N$大小的傅里叶系数矩阵,与空间域的图像大小一致。对$M\times N$的图像做傅里叶变换,就是要计算$M\times N$个傅里叶系数,每个傅里叶系数的计算公式上面已经给出。
一个傅里叶系数的计算需要两重循环,遍历空间域图像的所有值,时间复杂度为$O(M\times N)$。然后一共需要计算$M\times N$个傅里叶系数,因而对于$M\times N$大小的图像我们直接计算其傅里叶变换的时间复杂度是$O((M\times N))^2$。一般情况下$M$和$N$不会相差很远,因而这个时间复杂度可以说是四次方级别的。常见的图像大小$M=N=1024$,则需要执行万亿次 的基础计算。可以看到,这个时间复杂度实在是太高了。
快速傅里叶变换算法的提出使得傅里叶变换的时间复杂度降到了$O(MNlog_2(MN))$,耗费的时间大大减少,从而使得傅里叶变换开始在工业界得到了广泛的应用。下面是关于傅里叶变换和快速傅里叶变换的实现理论。
1、二维DFT的可分性 这里的DFT就是Discrete Fourier Transform即离散傅里叶变换的简称。二维的DFT可以分成两个方向上的一维变换,我们可以把二维离散傅里叶变换写成:
公式$(18)$首先对图像的每一行执行一维的傅里叶变换,得到中间的结果$F(x,v)$。然后公式$(19)$对公式$(18)$得到的结果$F(x,v)$执行逐列的一维傅里叶变换。即$f(x,y)$的二维DFT可以通过计算$f(x,y)$的每一行 的一维变换,得到中间结果,然后沿着中间结果的每一列 计算一维变换得到最终的结果。
注意上面的公式少了系数$1/(MN)$,这个系数$1/(MN)$可以灵活放置,可以放到傅里叶正变换的公式中,也可以放到傅里叶反变换的公式中,或者更为对称一点的做法就是正变换和反变换的系数均为$1/\sqrt{(MN)}$,只要保证正变换和反变换前面的常量系数乘起来等于$1/MN$即可。但是灵活放置不意味着可以直接去掉。
2、用DFT算法计算IDFT 这里的IDFT就是Inverse Discrete Fourier Transform即离散傅里叶反变换的简称。二维的IDFT计算公式的形式如下:
仔细观察傅里叶正变换和反变换的差别,可以发现,我们可以采用傅里叶正变换的形式来表示反变换,对上面的公式两边取复共轭,并乘上$MN$,有:
此时,在公式$(20)$的右边,我们具有与正变换相同的形式,与正变换的区别就是正变换的输入是$f(x,y)$,而这里的输入是$F(\mu,v)$的复共轭$F’(\mu,v)$。通过公式$(20)$我们可以得到$MNf’(x,y)$,然后将其除以$MN$再取复共轭就得到了$f(x,y)$(如果$f(x,y)$本身就是实函数的话,例如我们的图像都是实函数,取复共轭其实就是它自身)。因此,我们可以通过将$F’(\mu,v)$输入到正变换的算法中,得到$MNf’(x,y)$,再除以$MN$并取复共轭就得到了时空域的函数。即我们用用DFT算法来计算IDFT。
3、快速傅里叶变换 前面我们已知二维的DFT可划分成一维的DFT计算,因此接下来的快速傅里叶变换我们只考虑一维的DFT。快速傅里叶变换的英文名是Fast Fourier Transform,因此简称为FFT。由前面可知,一维的DFT计算公式如下:
为了便于讨论,我们记$W_M^{\mu x}$为:
设$M$是$2$的幂次方,即存在正整数$n$,使得$M=2^n$。因此可以将$M$分成两半,即$M=2K$,$K$也是正整数。将$M=2K$代入公式$(21)$有:
根据公式$(22)$易证$W^{2\mu x}_{2K}=W^{ux}_K$,所以$(23)$可以表示成:
定义$F_{even}(\mu)$和$F_{odd}(\mu)$如下:
其中的$\mu=0,1,2,…,K-1$,注意这里不是$0,1,2…,M-1$了。公式$(24)$可以简写如下:
公式$(26)$给出了前半部分的计算公式。又因为$W_M^{\mu + M}=W_M^\mu$和$W_{2M}^{\mu + M}=-W_{2M}^\mu$(这两个可以仔细地根据公式$(22)$推导得到),我们可以得到后半部分的计算公式:
可以看到,我们将原$\mu=0,1,2,…,M-1$的函数值划分成偶数部分和奇数部分,分别对偶数部分和奇数部分做傅里叶变换得到公式$(25)$,最后的结果是根据公式$(25)$的结果做一些合并得到(即公式$(26)$和公式$(27)$)。原来一维的傅里叶变换计算量为$M^2=4K^2$,采用上面的方法我们仅需要计算两个长度为$K$的傅里叶变换,因而计算量就变为$K^2+K^2=2K^2$,显然易见,计算量降低为原来的一半。这是一个非常大的优化。
将一个大的问题划分成两个规模一样、问题相似的子问题,这个其实就是分治算法的策略。上面仅仅讨论了一次划分,我们还可以继续对$F_{even}(\mu)$和$F_{odd}(\mu)$做一样的分割问题操作。这样一直递归下去,直到问题的规模变为$2$,这时直接采用公式$(21)$计算,然后自底向上逐次合并成原问题,最后的合并得到最终解 。
只要规模不是小于一定的程度,则每个子问题可以继续划分成两个更小的子问题,如此递归划分下去,构成了一颗满二叉树 ,该满二叉树的高度为$log_2(M)$。二叉树树一层的所有的节点合并需要的时间复杂是$O(M)$,因而最终总共需要的时间就是树的高度乘上每一层合并需要的时间,即$O(Mlog_2(M))$ 。采用FFT算法的时间复杂度由原来的$O(M^2)$降低到$O(Mlog_2 M)$。
4、实现代码 理清了整个算法思路之后,我们就可以很容易地实现FFT算法了。
首先是算法的输入,为了将DFT和IDFT结合起来,我们将算法的输入设为复数元素的矩阵。进行DFT正变换时将图像的像素值赋值到复数元素的实部,虚部为$0$,构成实部为灰度值、虚部为$0$的复数元素矩阵;进行反变换时输入傅里叶系数矩阵,做相应的操作。因此,我们首先定义一个复数元素矩阵:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 class ComplexMatrix { public : ComplexMatrix() = default ; ComplexMatrix(const Image &image); ComplexMatrix(int row, int col, const Complex &value = Complex()); ComplexMatrix(const ComplexMatrix &other); int getRow () const int getCol () const Complex *getRawData () ; Complex operator () (int r, int c) const ; std ::vector <Complex> getRowData(int r) const ; std ::vector <Complex> getColData(int c) const ; void multiply (const double &value) void conjugated () void set (int r, int c, const Complex &value) void setRowData (int r, const std ::vector <Complex> &value) void setColData (int c, const std ::vector <Complex> &value) private : std ::vector <std ::vector <Complex>> data; }; ComplexMatrix::ComplexMatrix(const Image& image) { int row = image.height(); int col = image.width(); data.resize(row, std ::vector <Complex>(col)); for (size_t r = 0 ; r < row; ++r) for (size_t c = 0 ; c < col; ++c) this ->set (r, c, Complex(image(c, r).r * pow (-1.0 , r + c), 0.0 )); } ComplexMatrix::ComplexMatrix(int row, int col, const Complex & value) { assert(row >= 0 && col >= 0 ); data.resize(row, std ::vector <Complex>(col, value)); } ComplexMatrix::ComplexMatrix(const ComplexMatrix & other) { int row = other.getRow(); int col = other.getCol(); data.resize(row, std ::vector <Complex>(col)); for (size_t r = 0 ; r < row; ++r) for (size_t c = 0 ; c < col; ++c) this ->set (r, c, other(r, c)); } Complex ComplexMatrix::operator ()(int r, int c) const { if (r < 0 || r >= getRow()) return Complex(); if (c < 0 || c >= getCol()) return Complex(); return data[r][c]; } std ::vector <Complex> ComplexMatrix::getRowData(int r) const { int col = getCol(); std ::vector <Complex> ret(col, Complex()); if (r < 0 || r >= getRow()) return ret; return data[r]; } std ::vector <Complex> ComplexMatrix::getColData(int c) const { int row = getRow(); std ::vector <Complex> ret(row, Complex()); if (c < 0 || c >= getCol()) return ret; for (size_t r = 0 ; r < row; ++r) ret[r] = (*this )(r, c); return ret; } void ComplexMatrix::multiply(const double & value){ int row = getRow(); int col = getCol(); for (size_t r = 0 ; r < row; ++r) for (size_t c = 0 ; c < col; ++c) this ->set (r, c, (*this )(r, c) * value); } void ComplexMatrix::conjugated(){ int row = getRow(); int col = getCol(); for (size_t r = 0 ; r < row; ++r) for (size_t c = 0 ; c < col; ++c) this ->set (r, c, (*this )(r, c).conjugate()); } int ComplexMatrix::getRow() const { return data.size(); }int ComplexMatrix::getCol() const { if (data.size() > 0 ) return data[0 ].size(); else return 0 ; } Complex * ComplexMatrix::getRawData() { return data.data()->data(); } void ComplexMatrix::set (int r, int c, const Complex & value){ if (r < 0 || r >= getRow()) return ; if (c < 0 || c >= getCol()) return ; data[r][c] = value; } void ComplexMatrix::setRowData(int r, const std ::vector <Complex>& value){ if (r < 0 || r >= getRow()) return ; assert(value.size() == getCol()); for (size_t c = 0 ; c < getCol(); ++c) this ->set (r, c, value[c]); } void ComplexMatrix::setColData(int c, const std ::vector <Complex>& value){ if (c < 0 || c >= getCol()) return ; assert(value.size() == getRow()); for (size_t r = 0 ; r < getRow(); ++r) this ->set (r, c, value[r]); }
然后实现一维的傅里叶变换,根据分治策略写好即可,这里目前我只实现了递归版本。递归虽然实现简单、简洁,但对性能不太友好,因为涉及到太多的函数调用和跳转,因此性能最佳的应该是将递归转成迭代版本(这里涉及到蝶形算法,暂不展开),自底向上逐步计算而非自顶向下展开 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 Complex FFT::W(const double & u, const double & x, const double & k) { double theta = -M_2_PI * u * x / k; return Complex(cos (theta), sin (theta)); } std ::vector <Complex> FFT::fourierTransform1D(const std ::vector <Complex>& samples){ std ::vector <Complex> result; if (samples.size() == 2 ) { result.resize(2 ); result[0 ] = samples[0 ] + samples[1 ]; result[1 ] = samples[0 ] - samples[1 ]; return result; } int M = samples.size(); int K = M / 2 ; std ::vector <Complex> oddSamples(K); std ::vector <Complex> evenSamples(K); for (size_t i = 0 ; i < K; ++i) { evenSamples[i] = samples[2 * i]; oddSamples[i] = samples[2 * i + 1 ]; } auto evenResult = fourierTransform1D(evenSamples); auto oddResult = fourierTransform1D(oddSamples); result.resize(M); for (size_t u = 0 ; u < K; ++u) { auto W_u_2K = W(static_cast <double >(u), 1.0 , static_cast <double >(M)); W_u_2K *= oddResult[u]; result[u] = evenResult[u] + W_u_2K; result[u + K] = evenResult[u] - W_u_2K; } return result; }
最后的二维就是在一维的基础上进行:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 ComplexMatrix FFT::fourierTransform2D(const ComplexMatrix & target) { ComplexMatrix result (target) ; size_t row = result.getRow(); size_t col = result.getCol(); for (size_t i = 0 ; i < row; ++i) { std ::vector <Complex> data = result.getRowData(i); auto value = fourierTransform1D(data); result.setRowData(i, value); } for (size_t i = 0 ; i < col; ++i) { std ::vector <Complex> data = result.getColData(i); auto value = fourierTransform1D(data); result.setColData(i, value); } result.multiply(1.0 / sqrt (row * col)); return result; }
傅里叶的正变换和反变换都根据上面的代码实现,只不过反变换需要额外的一些操作,但都不难:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 ComplexMatrix Image::fft2D(const ComplexMatrix & target, bool flag) { if (flag) { ComplexMatrix ret = FFT::fourierTransform2D(target); return ret; } else { ComplexMatrix tmp = target; tmp.conjugated(); ComplexMatrix ret = FFT::fourierTransform2D(tmp); ret.conjugated(); return ret; } }
最后还需要特别注意的是FFT假定输入的矩阵大小都是$2$的幂次方,但输入的图像并不一定是$2$的幂次方,因此对于不是$2$的幂次方的图像,需要做适当的填充:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 Image Image::expandToPowerOf2(const Image & target) { int width = target.width(); int height = target.height(); int basis = 2 ; while (basis < width) basis *= 2 ; width = basis; basis = 2 ; while (basis < height) basis *= 2 ; height = basis; Image result; result.initialize(width, height, target.channel()); for (size_t row = 0 ; row < height; ++row) { for (size_t col = 0 ; col < width; ++col) { if (row < target.height() && col < target.width()) { result.set (col, row, target(col, row)); } else result.set (col, row, Pixel(0 , 0 , 0 , 255 )); } } return result; }
最后的最后,可能需要将图像的频谱输出,简单计算傅里叶系数矩阵的谱,并做一些适当的标定 (这个很重要,不然输出的频谱图看不出频率域的特征)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 Image Image::spectrumOfcomplexMatrix(const ComplexMatrix & target) { double tMax = -1 ; double tMin = FLT_MAX; Image output; output.initialize(target.getCol(), target.getRow(), 1 ); for (size_t row = 0 ; row < target.getRow(); ++row) { for (size_t col = 0 ; col < target.getCol(); ++col) { double gray = log2(target(row, col).length() + 1 ); tMax = std ::max(tMax, gray); tMin = std ::min(tMin, gray); } } for (size_t row = 0 ; row < target.getRow(); ++row) { for (size_t col = 0 ; col < target.getCol(); ++col) { Pixel tmp; tmp.a = 255 ; double gray = log2(target(row, col).length() + 1 ); gray = (gray - tMin) / (tMax - tMin) * 255 ; tmp.r = tmp.g = tmp.b = static_cast <unsigned char >(gray); output.set (col, row, tmp); } } return output; }
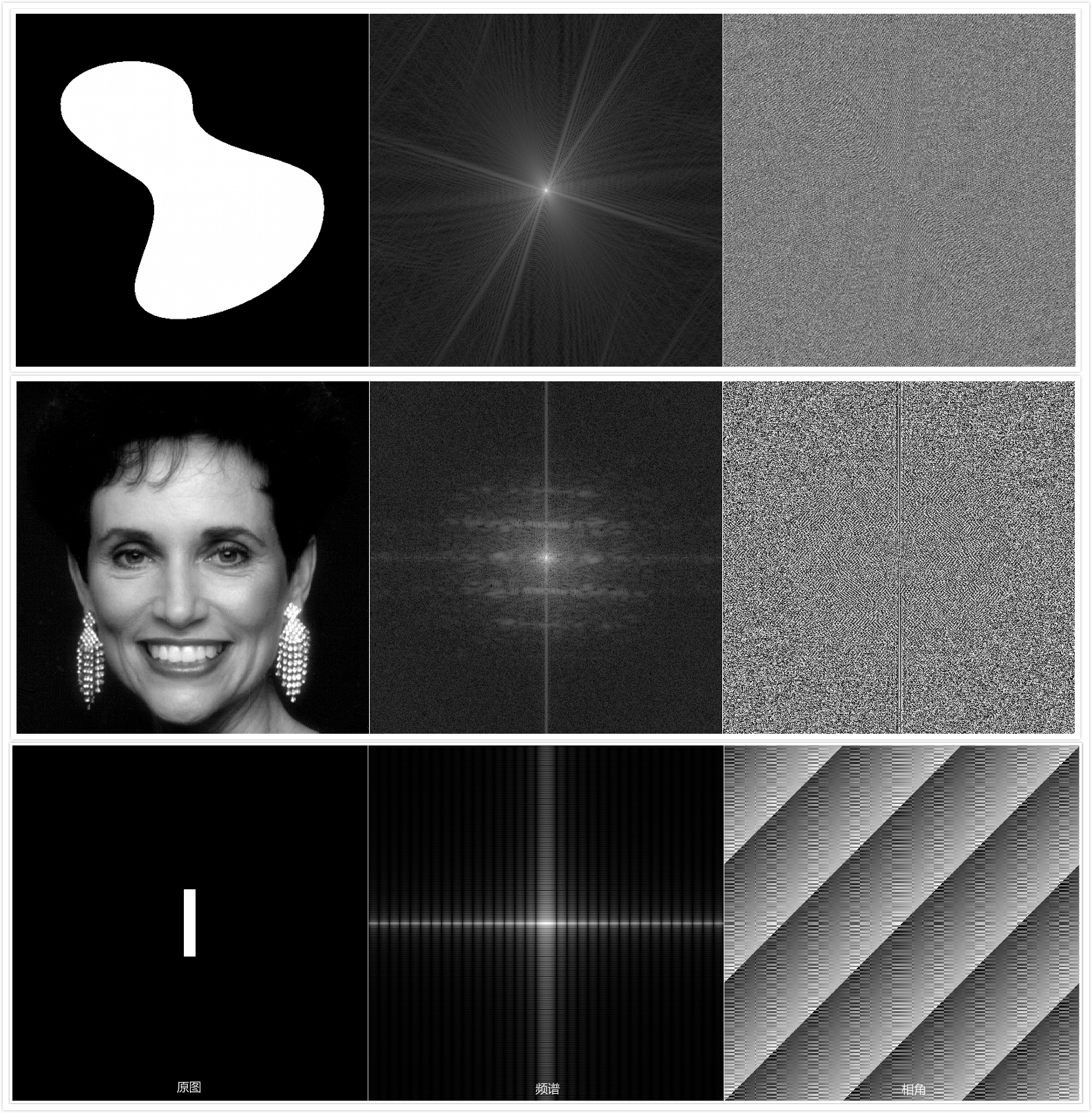
下面是一些程序的运行结果,左边是原图,中间是频谱图,右边是相角图。一般频谱图中心是最亮的,这是因为中心周围的值代表了低频分量,图像一般都是低频分量(平滑部分)比较多,高频分量(尖锐部分)比较少,因而四周比较暗。频谱值代表了原图的灰度值分布,而相角则蕴含了原图的形状内容,但是仅从频谱和相角无法从肉眼上知道原图的模样。
参考资料: $[1]$ (美)拉斐尔 C.冈萨雷斯(Rafael C.Gonzalez),理查德 E.伍兹(Richard E.Woods).数字图像处理 第3版 英文版[M].北京:电子工业出版社.2017.