在基于欧拉网格的烟雾模拟中,流体与自由面的接触面是一个模糊的边界,因此无需对烟雾的边界进行对流。但在液体模拟中,流体与自由面之间是有一个明确的边界,因此我们需要显式地跟踪这个流体边界来模拟液体的物理行为,基于水平集的自由表面流(Free-Surface Flow)是目前的主流方法。
流体表面的定义
流体的水平集对流
流体水平集的扭曲矫正
参考资料
Free-Surface Flow 在基于欧拉网格的烟雾模拟中,流体与自由面的接触面是一个模糊的边界,因此无需对烟雾的边界进行对流。但在液体模拟中,流体与自由面之间是有一个明确的边界,因此我们需要显式地跟踪这个流体边界来模拟液体的物理行为,基于水平集(Level set)的方法是目前的主流方法。
一、流体表面的定义 在基于粒子的流体模拟中,我们无需显式地定义液体与自由面的边界,流体粒子所占据的区域就是液体所在的区域。通过周围的流体粒子,我们能够确定给定的区域是否处于流体内部还是外部。但是在基于欧拉网格的流体模拟中,我们很难直接确定区域是处于流体内部还是外部,这是因为流体表面是连续可微的。如果直接给欧拉网格一个二值标量场,$0$表示流体外部,$1$表示流体内部,那么在流体的边界处该标量场不是连续的,因而也不是可微的。保证流体边界处连续可微对于模拟高质量的流体来说非常重要,这是因为流体表面张力或者计算法线向量的计算都需要在流体表面做一些微分算子。
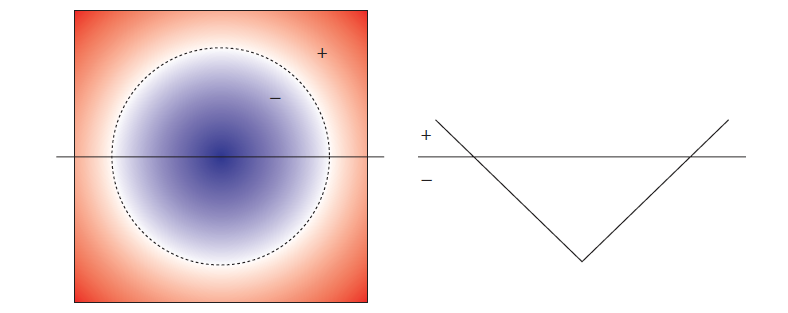
目前最为主流的方法就是采用隐式表面也就是符号距离场来表示流体的边界。隐式表面具有许多非常良好的性质。给定一个隐式表面的符号距离场函数$\phi(x)$,那么我们可以通过符号来判断一个区域是处于流体内部还是外部,隐式表面被定义在$\phi(x)=0$的零等值面上(如图1中的虚线)。$\phi(x)$的梯度满足如下方程(程函方程):
图1 符号距离场
符号距离场在表面附近的函数值是连续可微的,因而它能够表示连续平滑的流体表面。采用符号距离场来对物体表面进行建模的方法通常被称为水平集法(Level set method),目前水平集在各个领域都有涉及,流体模拟只是其中之一。通过将一个表面转换成符号距离场,我们可以非常容易地计算表面的一些几何性质。
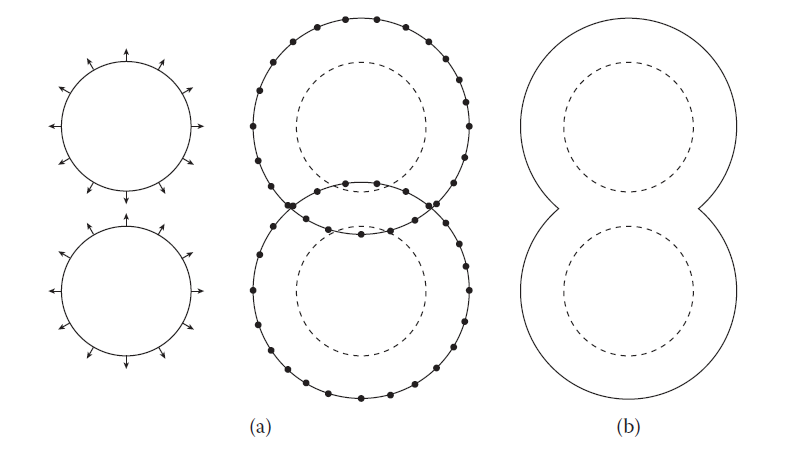
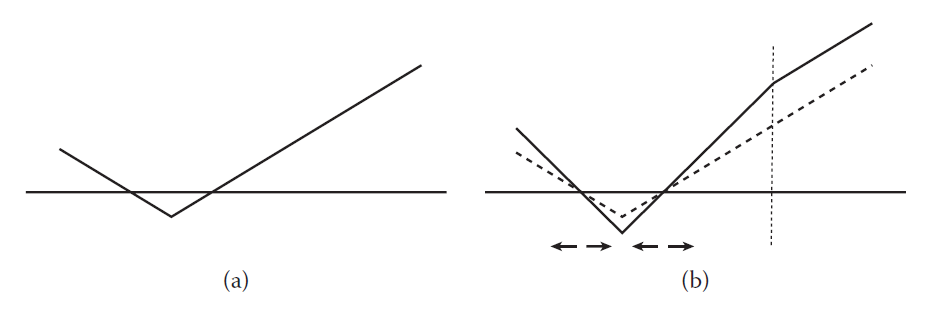
水平法一个非常有用的点就是它处理拓扑结构变化的能力。如下图2所示,这张图分别展示了显式表面和隐式表面在处理圆形表面扩张时的差别。圆形表面向外扩张时,显式表面需要将每一个网格点沿着法线向量向外挪动得到扩张后的几何体,而隐式表面只需将其相应的符号距离场值减去扩张距离即可。当几何体大到一定的程度时,两个圆形会产生相交的区域(在流体中表现为液滴相融),显式表面法需要逐个计算相交点,非常复杂且很容易出错;而隐式表面无需额外的特殊处理。这就是隐式表面的优势所在。
图2 (a)显式以及(b)隐式的圆形表面扩张
水平集法尽管在这里有众多优势,但是实现起来也没那么容易。采用水平集法跟踪流体表面需要解决两个主要问题。一个就是如何正确地追踪流体表面,这个其实就是一个流体对流问题;另外一个就是如何解决符号距离场对流带来的扭曲问题,这是因为在对流时我们不能够很好地保持符号距离场的几何性质。
二、流体的水平集对流 在对流步骤,流体的水平集与流体其他的标量场属性别无二致,因此我们只需将流体的水平集传入半拉格朗日对流解算器即可。但是因为流体的符号距离场并不是流体本身的物理属性,因此采用半拉格朗日法对符号距离场对流会在距离流体表面较远的地方带来一些扭曲的问题,这个我们稍后再看。
在常见的液体模拟中,实际上还有一个流体被我们忽略了,这个流体就是空气。普遍情况下,空气对液体的影响比较小,几乎可以忽略,因此一种简化的液体模拟模型——自由表面流(Free-Surface Flow)被提出。这种流体模拟假设空气对液体的压强、粘性作用很小,通常空气的压强被设置为某一个给定的常量值。这种液体模型是最简单的,但是也能够模拟出非常真实的液体。此外,还有一些模拟例如泡状流(Bubby Flow)能够模拟空气与液体的交互现象,这类流体模拟属于多相流模型(Multiphase Fluid Flow)。多相流在同一个系统中采用不同的密度、粘度系数等来模拟流体模拟多种不同的流体,因而较为复杂。
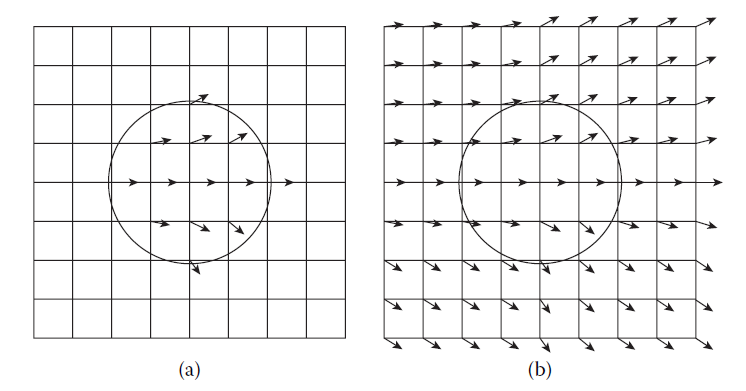
这里目前讨论的还是属于自由表面流,我们通过构建额外的流体水平集标量场来追踪流体的表面,流体的水平集和其他可对流的标量场一样在对流阶段采用半拉格朗日对流法进行对流。自由表面流直接忽略空气的流体量场,因此在对流时我们需要处理空气区域的速度场,因为自由表面流对空气区域的速度场是没有定义的,如下图3(a)所示,圆形区域是流体区域,在圆形区域外速度场无定义。但在半拉格朗日对流法中,由于其后向追踪的特性,我们有可能会追踪流体区域外部的空气区域去获取流体的速度场,因此我们需要做一个速度场外推(extrapolation)操作。
图3 (a)流体无外推的速度场,(b)外推后的速度场
将速度场从流体区域外推到空气区域与从流体区域外推到固体墙区域的过程类似,我们简单地采用诺伊曼边界条件,使速度场在法线方向上的变化率为零:
我们通过在法线方向外推流体的速度场来求解上述的边界条件。最大的外推距离取决于流体的CFL距离,超出CFL距离的外推没有意义,因为即便在边界处逆向追踪,其追踪的距离也不会超过CFL距离。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 void LevelSetLiquidSolver3::extrapolateVelocityToAir(double currentCfl){ auto sdf = signedDistanceField(); auto vel = gridSystemData()->velocity(); auto u = vel->uAccessor(); auto v = vel->vAccessor(); auto w = vel->wAccessor(); auto uPos = vel->uPosition(); auto vPos = vel->vPosition(); auto wPos = vel->wPosition(); Array3<char > uMarker(u.size()); Array3<char > vMarker(v.size()); Array3<char > wMarker(w.size()); uMarker.parallelForEachIndex([&](size_t i, size_t j, size_t k) { if (isInsideSdf(sdf->sample(uPos(i, j, k)))) uMarker(i, j, k) = 1 ; else { uMarker(i, j, k) = 0 ; u(i, j, k) = 0 ; } }); vMarker.parallelForEachIndex([&](size_t i, size_t j, size_t k) { if (isInsideSdf(sdf->sample(vPos(i, j, k)))) vMarker(i, j, k) = 1 ; else { vMarker(i, j, k) = 0 ; v(i, j, k) = 0 ; } }); wMarker.parallelForEachIndex([&](size_t i, size_t j, size_t k) { if (isInsideSdf(sdf->sample(wPos(i, j, k)))) wMarker(i, j, k) = 1 ; else { wMarker(i, j, k) = 0 ; w(i, j, k) = 0 ; } }); const Vector3D gridSpacing = sdf->gridSpacing(); const double h = max3(gridSpacing.x, gridSpacing.y, gridSpacing.z); const double maxDist = std ::max(2.0 * currentCfl, _minReinitializeDistance) * h; std ::cout << "Max velocity extrapolation distance: " << maxDist << std ::endl ; FmmLevelSetSolver3 fmmSolver; fmmSolver.extrapolate(*vel, *sdf, maxDist, vel.get()); applyBoundaryCondition(); }
有了外推值,我们就可以应用半拉格朗日对流解算器了。
1 2 3 4 5 6 7 8 9 10 void LevelSetLiquidSolver3::computeAdvection(double timeIntervalInSeconds){ double currentCfl = cfl(timeIntervalInSeconds); Timer timer; extrapolateVelocityToAir(currentCfl); std ::cout << "velocity extrapolation took " << timer.durationInSeconds() << " seconds\n" ; GridFluidSolver3::computeAdvection(timeIntervalInSeconds); }
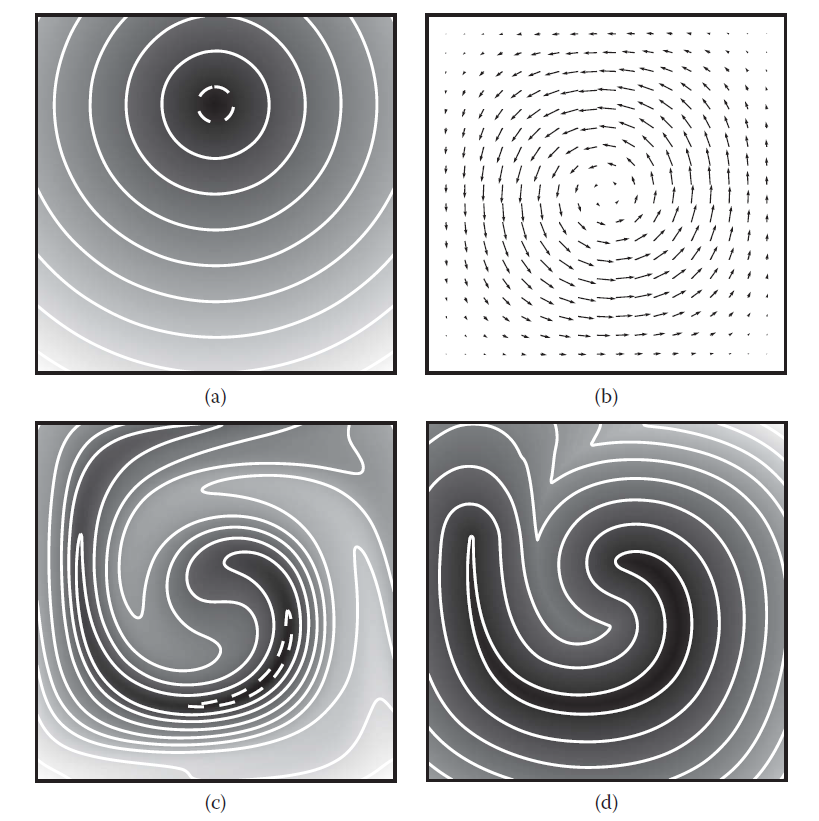
三、流体水平集的扭曲矫正 前面我们提到,由于流体的水平集并不是流体自身的物理属性,因而在进行半拉格朗日对流时我们没有办法很好地保证水平集的优良几何属性在对流过程中不被破坏。事实上,在经过对流之后,水平集在流体表面附近的几何属性依旧保持得很好,只是在距离表面比较远的地方它的符号距离场值不再代表当前的点到表面的最近距离(如下图4(c)所示),当然符号没有被破坏。注意到在流体表面处的符号距离场值被保持得很好,因此我们可以通过表面附近的值去修正远离表面的被扭曲的值(如下图4(d)所示)。
图4 (a)初始距离场,涡流(b)旋转导致距离场扭曲(c),复原后的距离场(d)
在经过对流之后,流体的符号距离场被扭曲的现象在数学上被解释为不再满足程函方程$|\nabla \phi(x)|=1$,即前面的公式$(1)$。但我们知道$\phi(x)$的符号依然是正确的,而且在流体表面附近$\phi(x)$依然是一个正确的值。因此为了恢复流体的符号距离场,一种暴力的方法就是遍历所有的欧拉网格点并找寻找其到表面的最近点,显然这种方法太过复杂暴力且非常耗时。我们可以采用一个相反的策略。
图5 (a)复原后的距离场,(b)距离场修复过程
以图5(b)的一维情况为例(图中的水平线是零等值线),因为在零等值线上的距离场是没有被扭曲的(图5(b)中的虚线与实线在零等高线处的梯度相等,虚线是修复的距离场),因此我们可以从零等值线附近的欧拉网格点出发,逐步扩散到其他网格点,在扩散的过程中累加距离场。在一维的情况中,扩散的方向就是左和右两个方向,通过这个扩散过程逐步矫正经过的网格点的符号距离场,最终得到正确的符号距离场(如图5(a)所示)。
这个矫正的过程实际上跟波在空间中的传播很类似,因此我们可以借鉴流体的对流方程并做一些修改:
其中$u$是速度场(注意这里的速度场不再是流体的速度场),$t$是一个伪时间轴(因为这并不是物理模拟,它属于几何处理)。与原对流方程不同,方程右边是$1$而不是$0$。当方程右边是$0$时,它表明$\phi$仅在速度场$u$的作用下变化;当方程右边是某个不为零的常量$c$时,它表明$\phi$在速度场$u$的作用下经过一个单位距离时$\phi$的增量为$c$。因此令方程右边的$c=1$就是使得$\phi$在速度场$u$的作用下经过一个单位距离时$\phi$的增量就是一个单位的距离。
公式$(3)$中的速度场就是传播速度,我们令其沿着表面的法线方向传播。我们根据隐式表面的符号距离场计算表面的单位法线向量:
在远离表面被扭曲的地方采用公式$(4)$计算法线向量显然会带来一些误差,这些暂且不管。将公式$(3)$中的$u$替换为公式$(4)$的法线场:
然后公式$(5)$可以进一步简化为:
需要注意公式$(6)$仅适用于正距离场区域(也就是流体外部区域),对于负距离场区域,我们将采用的是下面的公式:
把公式$(6)$和公式$(7)$合并一起,可以写成如下的形式:
公式$(8)$其实不难理解。如果我们有一个正确的符号距离场,那么其满足方程$|\nabla \phi|=1$即$|\nabla \phi|-1=0$,此时由公式$(8)$可知$\frac{\partial \phi}{\partial t}=0$,这意味着$\phi$不会发生变化,这也正是我们想要的(因为不需要矫正了)。而若$\phi$产生了一下扭曲,导致一些区域的$|\nabla \phi|\neq 1$,这就是说$|\nabla\phi|-1\neq 0$,这个相当于一个误差项使得我们的距离场朝着误差项减小的方向变化,最终达到$|\nabla \phi|=1$。
最后就是关于公式$(8)$的实现了,我们通过迭代的方式来实现公式$(8)$,设置一个时间步长和迭代次数,在每一次的迭代中计算当前的$\frac{\partial \phi}{\partial t}$,然后采用一个显式欧拉积分更新流体的水平集。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 void IterativeLevelSetSolver3::reinitialize( const ScalarGrid3& inputSdf, double maxDistance, ScalarGrid3* outputSdf) { const Size3 size = inputSdf.dataSize(); const Vector3D gridSpacing = inputSdf.gridSpacing(); ArrayAccessor3<double > outputAcc = outputSdf->dataAccessor(); const double dtau = pseudoTimeStep(inputSdf.constDataAccessor(), gridSpacing); const unsigned int numberOfIterations = distanceToNumberOfIterations(maxDistance, dtau); copyRange3(inputSdf.constDataAccessor(), size.x, size.y, size.z, &outputAcc); Array3<double > temp(size); ArrayAccessor3<double > tempAcc = temp.accessor(); std ::cout << "Reinitializing with pseudoTimeStep: " << dtau << " numberOfIterations: " << numberOfIterations << std ::endl ; for (unsigned int n = 0 ; n < numberOfIterations; ++n) { inputSdf.parallelForEachDataPointIndex( [&](size_t i, size_t j, size_t k) { double s = sign(outputAcc, gridSpacing, i, j, k); std ::array <double , 2 > dx, dy, dz; getDerivatives(outputAcc, gridSpacing, i, j, k, &dx, &dy, &dz); double val = outputAcc(i, j, k) - dtau * std ::max(s, 0.0 ) * (std ::sqrt ( square(std ::max(dx[0 ], 0.0 )) + square(std ::min(dx[1 ], 0.0 )) + square(std ::max(dy[0 ], 0.0 )) + square(std ::min(dy[1 ], 0.0 )) + square(std ::max(dz[0 ], 0.0 )) + square(std ::min(dz[1 ], 0.0 ))) - 1.0 ) - dtau * std ::min(s, 0.0 ) * (std ::sqrt (square(std ::min(dx[0 ], 0.0 )) + square(std ::max(dx[1 ], 0.0 )) + square(std ::min(dy[0 ], 0.0 )) + square(std ::max(dy[1 ], 0.0 )) + square(std ::min(dz[0 ], 0.0 )) + square(std ::max(dz[1 ], 0.0 ))) - 1.0 ); tempAcc(i, j, k) = val; }); std ::swap(tempAcc, outputAcc); } auto outputSdfAcc = outputSdf->dataAccessor(); copyRange3(outputAcc, size.x, size.y, size.z, &outputSdfAcc); }
在计算符号的函数中,为了获取更加平滑的效果,我们采用一个更加平滑的符号计算方法,如下所示,其中$h$是网格单元的边长:
1 2 3 4 5 6 7 8 9 10 11 double IterativeLevelSetSolver3::sign( const ConstArrayAccessor3<double >& sdf, const Vector3D& gridSpacing, size_t i, size_t j, size_t k) { double d = sdf(i, j, k); double e = min3(gridSpacing.x, gridSpacing.y, gridSpacing.z); return d / std ::sqrt (d * d + e * e); }
然后紧接着我们用getDerivatives计算$\phi$的梯度$\nabla \phi$,一种逆风法就是计算两个单边的差分,然后根据符号选择采用两个差分结果中的一个。最后根据符号以及梯度,在给定的时间步长下,我们更新每一个网格点的符号距离场值:
最后还有个时间步长的选取,如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 double IterativeLevelSetSolver3::pseudoTimeStep( ConstArrayAccessor3<double > sdf, const Vector3D& gridSpacing) { const Size3 size = sdf.size(); const double h = max3(gridSpacing.x, gridSpacing.y, gridSpacing.z); double maxS = -std ::numeric_limits<double >::max(); double dtau = _maxCfl * h; for (size_t k = 0 ; k < size.z; ++k) { for (size_t j = 0 ; j < size.y; ++j) { for (size_t i = 0 ; i < size.x; ++i) { double s = sign(sdf, gridSpacing, i, j, k); maxS = std ::max(s, maxS); } } } while (dtau * maxS / h > _maxCfl) dtau *= 0.5 ; return dtau; } unsigned int IterativeLevelSetSolver3::distanceToNumberOfIterations( double distance, double dtau) { return static_cast <unsigned int >(std ::ceil (distance / dtau)); }
这种迭代的方法非常有意思,在一层一层的迭代中,距离场的函数逐渐地被恢复原样、不再扭曲。符号距离场的这个恢复过程被称为重初始化(reinitialization)。在每一帧的对流之后,我们都要调用这个过程来复原真正的符号距离场,重初始化的范围我们取当前的CFL距离,因为超出CFL距离的重初始化没有意义。
1 2 3 4 5 6 7 8 9 10 void LevelSetLiquidSolver3::onEndAdvanceTimeStep(double timeIntervalInSeconds){ double currentCfl = cfl(timeIntervalInSeconds); Timer timer; reinitialize(currentCfl); std ::cout << "reinitializing level set field took " << timer.durationInSeconds() << " seconds\n" ; ...... }
参考资料: $[1]$ Kim, D. (2017). Fluid engine development . Boca Raton: Taylor & Francis, a CRC Press, Taylor & Francis Group.