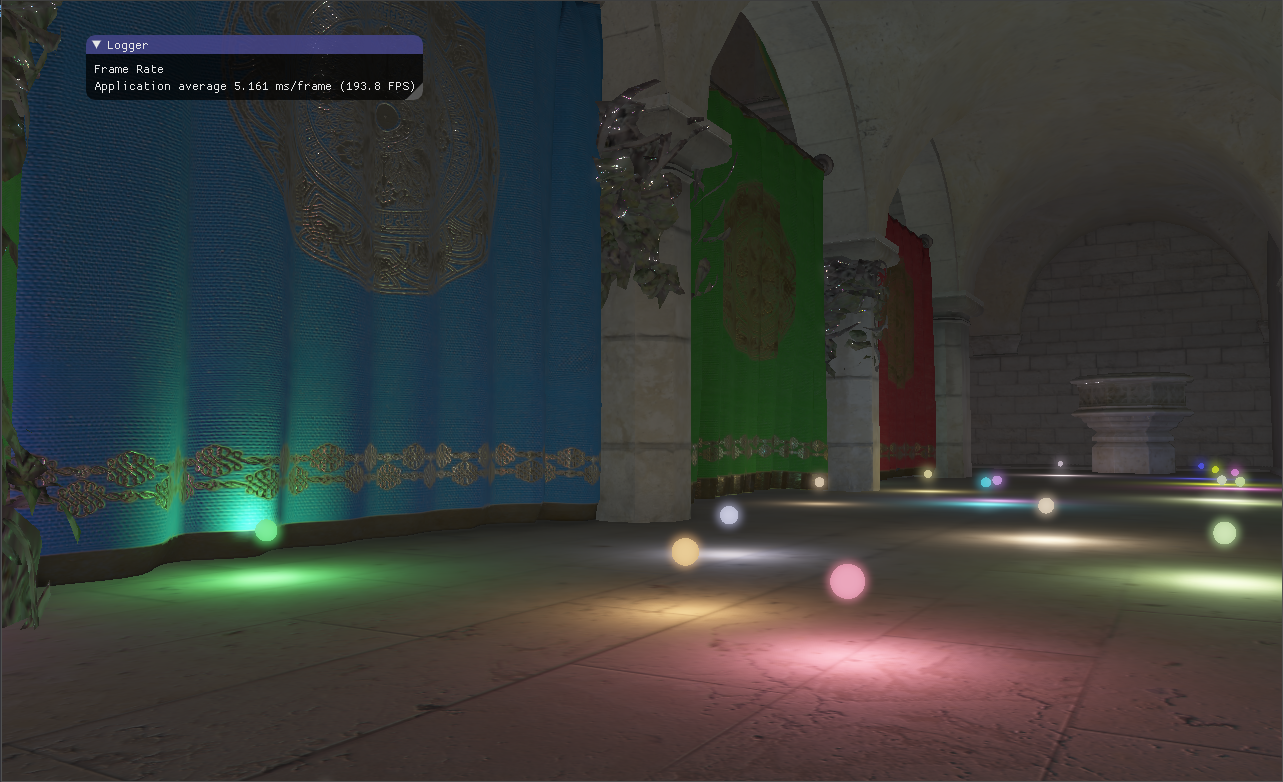
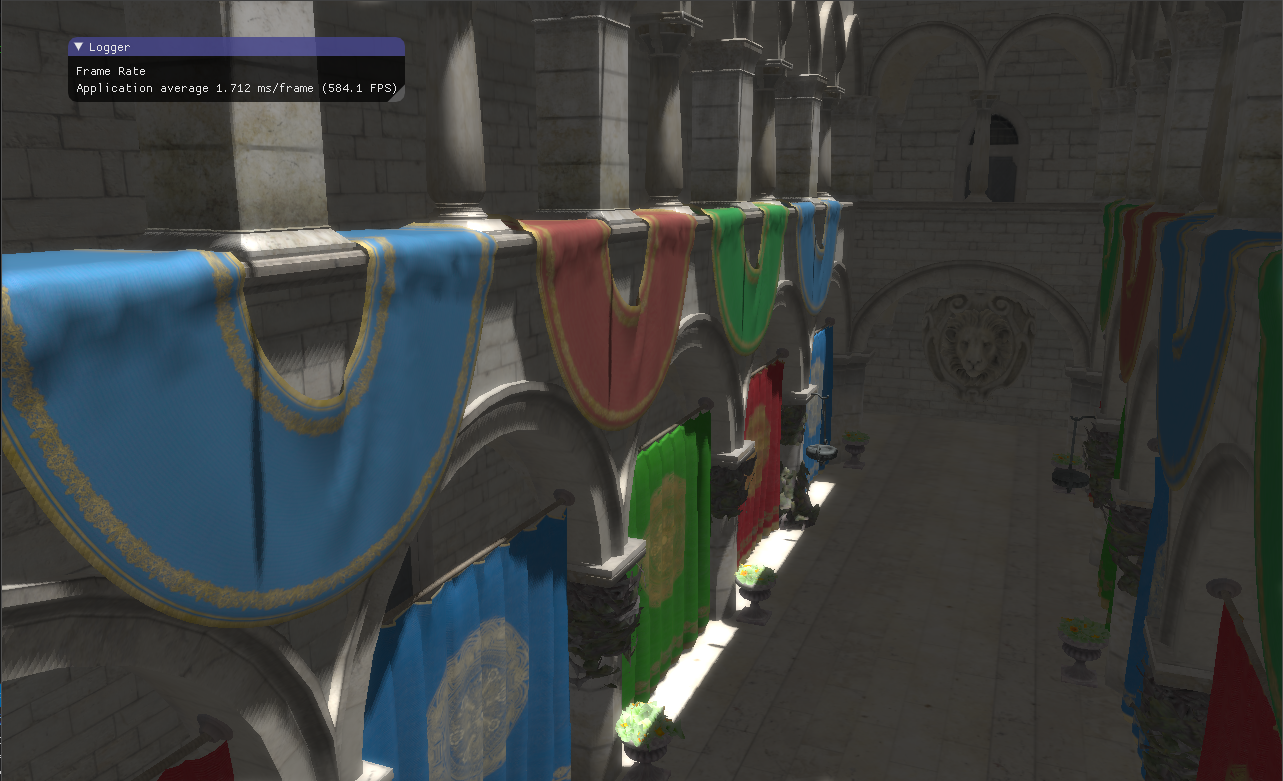
本文采用OpenGL搭建了一个基于物理着色的渲染器,目前大多数的实时应用都是采用了PBR,相对于传统的Phong等基于经验的光照模型,基于物理着色的渲染方法更为真实。
基于物理的渲染(Physically Based Rendering,简称PBR)技术致力于渲染出更贴近于真实物理世界的光影效果,它倾向于探索光影背后的物理规律,然后在此基础上构建一个基于物理规律的光照模型,最后应用到光照计算中。基于物理的渲染除了更为真实,它也给光照计算的赋予了更多的物理意义,从而使得设计师们摆脱基于经验的参数调整,只要设置的物理量正确,则最终光照效果也将会是正确的。即便如此,基于物理的渲染技术依然只是现实物理世界的一个逼近。对于一个基于物理渲染的光照模型,它通常需要满足以下的三个条件:
1、能量守恒
2、基于微平面的表面模型
3、使用基于物理的BRDF
接下来我们就按照上面的顺序一一展开。
## 一、能量守恒(Energy Conservation)
基于物理的光照模型必须遵守这样的一个能量守恒原则:对于一个非自发光的物体,出射光线的能量永远不能超过入射光线的能量。当一束光线照射到物体表面,它就被分割成两个部分,分别是折射部分和反射部分。反射部分的光线则是直接撞击到表面然后反弹开来的那部分光线,这部分构成中我们日常生活中常见的镜面高光。折射部分的光线则进入物体内部,光线在内部与物体的粒子发生碰撞,此时光线的一部分能量就转变成热能。一般情况下,并非所有光能都被转化成热能,还有一些光线在内部经过多次散射最终又离开物体表面,这部分的光线构成了物体的漫反射光。这里还要特别区分一下金属材质,与非金属材质和电介质不同,金属材质会直接吸收折射光而不会散开,只表现出镜面反射光。即金属表面不会显示出漫反射的颜色。
根据能量守恒的原则,反射光与折射光是相互排斥的,因此我们只要知道其中一部分占总入射光的百分比,就能立马得到另外一部分的能量占比。通过这样的一个方案,我们就能保证出射光的总能量小于等于入射光的总能量。下面的图1展示Blin-Phong的光照渲染结果,Blin-Phong光照模型并不是一个基于物理的光照模型,它并不满足能量守恒的原则,可以看到,图1场景看起来太亮了,而我仅仅将光照的辐射率设置为vec3(0.6)。
图1 Blin-Phong光照模型的渲染结果
二、微平面模型(Microfacet Model) PBR技术采用了微平面理论:在微观尺度下,任意的一个平面都可以用一组微小的光滑镜面来描述,这个微小的光滑镜面就是微平面(Microfacet)。根据平面粗糙程度的不同,这些微平面的排列取向也各不相同。一个平面越是粗糙,则其平面上的微平面排列就越混乱。微平面的排列越混乱,则入射光线照射到该平面上时更趋向于朝向完全不同的方向散射开来,从而产生更大范围的镜面光。同理,若平面越光滑,则其微平面排列取向越规整,入射光线大体上越趋向于向同一个方向反射,产生更小范围、更加锐利的镜面高光。正如如下图2所示。
图2 粗糙和光滑的微平面
微平面的取向排列混乱程度我们采用一个粗糙度(Roughness)的参数来衡量。直接在微观尺度下操作显然不可行,因为我们将在宏观尺度下采用统计学的方法来估算微平面的粗糙度。这个粗糙度我们定义为某个向量的方向与微平面平均取向方向一致的概率,这个向量便是光线向量$l$和视线向量$v$之间的中间向量$h$:
在一个表面的微平面中,越多微平面的法线方向与中间向量的方向一致,则镜面的反射效果就越强烈、越锐利。
图3 不同粗糙度的镜面高光
三、基于物理的BRDF 在前面的能量守恒原则和微平面理论的基础上,我们将展开基于物理的光照计算。首先我们要了解的是渲染方程,PBR采用的渲染方程是一个特化版本,也被称为反射方程,如下所示:
上式中,$L_o$是反射辐射率,$L_i$是入射辐射率,$p$为物体表面上的一点,$\omega_o$为出射方向向量,$\omega_i$为入射方向向量,$n$是表面法线向量,$f_r(p,\omega_i,\omega_o)$是后面我们将要提到的BRDF函数。积分区域$\Omega$是以表面法线$n$为轴的半球领域。PBR渲染方程主要是关于光能辐射度量学的(Radiometry)的内容,这里简单介绍一些辐射度量学的物理量。
辐射通量(Radiant Flux) :辐射通量以瓦特为单位,符号为$\Phi$,它衡量一个光源所辐射的能量。光是由多种不同波长的能量所集合而成的,一个光源所放射出来的能量可以被视作这个光源包含的所有各种波长的一个函数。但是在计算机图形学中,我们通常采用三原色编码即RGB来简化辐射通量的表示,这套编码带来的损失基本可以忽略。
立体角(Solid Angle) :这个物理量在前面的文章都有提及过了,立体角符号为$\omega$,它描述了一个几何体投影到单位球面上的大小,立体角可以看成是带有体积的方向向量。
辐射强度(Radiant Intensity) :辐射强度衡量了在单位球面上,一个光源每单位立体角所辐射的辐射通量。其定义公式为$I=\frac{d\Phi}{d\omega}$,即微分辐射通量除以微分立体角。对于一个全向且向所有方向均匀辐射的光源,辐射强度表示了光源在一个单位球面上单位立体角的辐射能量。
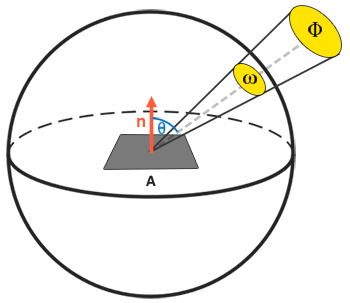
辐射率(Radiance) :辐射率就是具有辐射强度$\Phi$的光源在单位面积$A$、单位立体角$\omega$下的辐射总能量,其定义见下面的公式$(3)$。$d\omega cos\theta$将单位立体角(也就是单位球体上的面积)投影到法线方向。
图4 辐射率示意图
辐射率是辐射度量学上表示一个区域平面上光线总量的物理量,它受到入射光线与平面法线间的夹角$\theta$的余弦值$cos\theta$的影响:当直接辐射到平面上的程度越低时,光线就越弱,而当光线完全垂直于平面时强度最高。当立体角$\omega$和面积$A$趋向于无穷小时,我们能用辐射率来表示单束光线穿过空间中的一个点的通量。这就使我们可以计算得出作用于单个片段或点上的单束光线的辐射率,即把立体角$\omega$转变为方向向量然后把面$A$转换为点$p$,这样我们就能直接在我们的着色器中使用辐射率来计算单束光线对每个片段的作用。
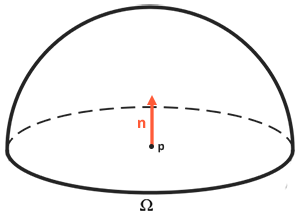
上面讨论的仅仅是一束光线投射到点$p$上,但是通常我们需要计算的是所有投射到点$p$上的光线总和,这个和就是辐照度(Irradiance)。注意到反射方程$(2)$对半球领域$\Omega$进行积分,这是因为我们要计算的不只是单一一个方向上的入射光,而是一个以点$p$为球心、以法向为中轴的半球领域$\Omega$内所有方向上的入射光。
图5 半球领域
由于渲染方程都没有解析解,求解公式$(2)$即反射方程时我们将采用离散的方法来积分的数值解。目前常用的就是梯形法,在半球领域$\Omega$按一定的步长将反射率方程分散求解,然后再按照步长大小将所得的结果平均化,这个就是黎曼和(Riemann Sum)。
然后剩下的就是BRDF函数,也就是公式$(2)$中的$f_r(p,\omega_i,\omega_o)$部分。BRDF的全称为Bidirectional Reflective Distribution Function,即双向反射分布函数。对于一个给定材质属性,BRDF函数给出了入射光和反射光的关系,一束给定入射方向的入射光照射到物体表面时,会被反射到表面半球范围内的各个方向,不同反射角度的反射光线在入射光线中的占比各不相同,BRDF函数就用来表示这种比例关系,其定义如下:
Cook-Torrance模型是目前应用最为广泛的基于物理的BRDF模型,它被用于很多实时渲染管线的材质和光照环境下。Cook-Torrance的BRDF包含漫反射和镜面反射两个部分,其中的镜面反射部分比较复杂:
其中,$k_d$就是前面提到的入射光线中被折射的光线部分的能量占比,而$k_s$则是被反射的光线部分所占的比例。$f_{lambert}$是BRDF的漫反射部分,这个是Lambertian漫反射模型,其计算公式如下所示:
其中$c$是物体的反照率(Albedo),大部分的实时渲染应用都采用了Lambertian漫反射模型。然后就是镜面反射部分,镜面反射部分就是Cook-Torrance的各向同性光照模型:
其中$\omega_i$是入射方向,$\omega_o$是观察方向。Cook-Torrance的模型包含三个函数,D、F、G分别是法线分布函数、菲尼尔方程、几何函数。接下来我们将讨论的是Trowbridge-Reitz GGX法线分布函数,Fresnel-Schlick菲涅尔方程以及Smith’s Schlick-GGX几何函数。
首先是法线分布函数(Normal Distribution Function) ,给定表面的粗糙度,法线分布函数估算平面法线取向与中间向量一致的微平面数量。从统计学上讲,法线分布函数近似地描述了与中间向量$h$取向相同的微平面占全部微平面的比例。例如,给定中间向量$h$,若我们要估算的微平面中有$35\%$与向量$h$取向相同,那么法线分布函数将返回$0.35$。Trowbridge-Reitz GGX法线分布函数的数学定义如下所示:
其中,$n$为宏观法线,$h$是中间向量,而$\alpha$则表示平面的粗糙度。当粗糙度$\alpha$值很低时,即表面比较光滑时,与中间向量$h$取向相同的微平面会高度地集中在一个小半径范围内。此时镜面反射会形成一个非常明亮的光斑。相反,当表面的粗糙度值较高时,与$h$向量取向一致的微平面分布在一个比较大的半径范围内,这使得最终的镜面反射效果显得较为灰暗。
然后就是菲涅尔方程(Fresnel Equation) ,描述了指定角度下表面反射的光线所占的比例。当一束光线照射到表面时,菲涅尔方程会依据观察角度给出反射光线所占的百分比。然后根据这个反射光所占的百分比和能量守恒定律就可以得出光线折射部分所占的比率。当我们垂直观察物体的时候,任何表面都有一个基础的反射率。例如,用垂直的视角看向木制桌面或者金属桌面,此时只有最基本的反射,但若近乎与平面平行的角度去观察的话就会看到非常明显的反光效果。Fresnel-Schlick近似菲涅尔方程如下所示:
其中,$F_0$就是表面的基础反射率,它是通过折射系数计算得到的,$h$即前面提到的中间向量,$v$为观察方向向量。
最后就是几何函数(Geometry Function) ,几何函数描述了微平面自我遮挡的属性。当一个平面比较粗糙的时候,表面上的微平面可能会挡住其他的微平面从而减弱表面反射光的强度。与法线分布函数类似,几何函数也是从统计学的角度近似求出微平面之间相互遮蔽的比率。
图6 微平面的相互遮蔽现象
几何函数也采用一个材质的粗糙度作为输入的参数,越粗糙的表面其微平面之间相互遮挡的概率也就越高。Schlick-GGX几何函数的数学定义如下:
公式$(10)$中的$k$是关于粗糙度$\alpha$的重映射,取决于几何函数是针对直接光照还是针对IBL(Image Based Lighting)光照:
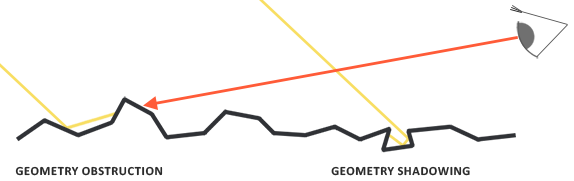
微平面的相互遮蔽主要有两个方面,分别是几何遮蔽(Geometry Obstruction)和几何阴影(Geometry Shadowing),几何遮蔽与视线向量有关,而几何阴影则于入射方向向量相关。我们采用史密斯法将两者纳入其中:
最终,我们得到反射方程$(2)$中的BRDF计算公式:
实际上,BRDF的计算公式$(13)$有个错误,公式中的$F$即菲涅尔项就是$k_s$,因为菲涅尔项表示的就是反射光线的占比,因此应该把$k_s$去掉,然后$k_d=1-F$。
将公式$(14)$代入到公式$(2)$中,我们最终得到一个具体的渲染方程:
三、PBR渲染器的实现 有了前面的理论基础,接下来我们就展开相关的PBR实现。首先我们要讨论的是PBR材质,仔细观察渲染方程公式$(15)$,求解这个渲染方程我们需要获取物体的反照率向量、法线向量、粗糙度。除此之外,我还需要物体的金属度参数,这是因为Fresnel-Schlick近似仅仅对电介质或者说非金属表面有定义,对于导体(Conductor)表面(金属),使用它们的折射指数计算基础折射率并不能得出正确的结果。金属度用来描述一个材质表面是金属还是非金属的,基于金属表面特性,我们要么使用电介质的基础反射率要么就使用物体的表面颜色。因为金属表面会吸收所有折射光线而没有漫反射,所以我们可以直接使用表面颜色纹理来作为它们的基础反射率。
因此,对于一个PBR渲染器,我们需要获取物体的PBR材质,PBR材质包含了反照率(Albedo)纹理、法线(Normal)纹理、粗糙度(Roughness)纹理以及金属度(Metallic)纹理,正如如下图7所示。在一些PBR渲染器中,还有一个环境遮蔽光贴图(Ambient Occulsion),这里我们不考虑AO贴图,而是考虑在后面采用SSAO实现环境遮蔽光的效果。
图7 PBR材质
然后还需要提一点的是,我们目前仅考虑直接光照部分,不考虑反弹多次的间接光照。仅考虑直接光照时,对于渲染方程$(15)$,我们不需要对整个半球领域进行积分,因为此时的被积函数是一个狄拉克函数。也就是被积函数仅在某一个特定的方向上才不为0,剩余部分函数值全为0,因此没有必要进行积分。在光照计算中,我们是可以直接知道空间中的光源位置,因此可以直接计算。当空间中有多个光源时,渲染方程的值就是直接计算点与这些光源之间的被击函数值最后累加起来。
公式$(16)$就是场景中有$m$个光源时的实际渲染方程。为了支持大量的光源,我采用了延迟渲染,将物体空间位置和PBR材质信息存储到多张纹理中,然后在屏幕空间计算光照。首先将物体的信息渲染到纹理中,因为采用了法线贴图,所以要在顶点着色器中构建TBN矩阵提取出法线向量:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 ---------------Vertex Shader------------------- #version 330 core layout (location = 0 ) in vec3 position; layout (location = 1 ) in vec3 normal; layout (location = 2 ) in vec2 texcoord; layout (location = 3 ) in vec3 color; layout (location = 4 ) in vec3 tangent; layout (location = 5 ) in vec3 bitangent; layout (location = 6 ) in mat4 instanceMatrix; out vec3 FragPos; out vec2 Texcoord; out mat3 TBNMatrix; uniform bool instance; uniform mat4 modelMatrix; uniform mat4 viewMatrix; uniform mat4 projectMatrix; uniform mat4 normalMatrix; uniform mat4 lightSpaceMatrix; void main () vec3 T = normalize(vec3(modelMatrix * vec4(tangent, 0.0f ))); vec3 B = normalize(vec3(modelMatrix * vec4(bitangent, 0.0f ))); vec3 N = normalize(vec3(modelMatrix * vec4(normal, 0.0f ))); TBNMatrix = mat3(T, B, N); Texcoord = texcoord; if (!instance) FragPos = vec3(modelMatrix * vec4(position,1.0f )); else FragPos = vec3(modelMatrix * instanceMatrix * vec4(position,1.0f )); gl_Position = projectMatrix * viewMatrix * vec4(FragPos,1.0f ); } ---------------Fragment Shader------------------- #version 330 core in vec3 FragPos; in vec2 Texcoord; in mat3 TBNMatrix; uniform float nearPlane; uniform float farPlane; uniform sampler2D albedoMap; uniform sampler2D normalMap; uniform sampler2D roughMap; uniform sampler2D metallicMap; uniform sampler2D depthMap; layout(location = 0 ) out vec3 dposition; layout(location = 1 ) out vec3 dnormal; layout(location = 2 ) out vec3 dalbedo; layout(location = 3 ) out vec3 droughness; void main () vec3 albedo = texture(albedoMap, Texcoord).rgb; vec3 normal = normalize(2.0f * texture(normalMap, Texcoord).rgb - vec3(1.0f )); normal = TBNMatrix * normal; float roughness = texture(roughMap, Texcoord).r; float metallic = texture(metallicMap, Texcoord).r; dposition = FragPos; dnormal = normal; dalbedo = albedo; droughness = vec3(roughness, metallic, gl_FragCoord.z); }
然后在屏幕空间中实现我们的PBR算法。首先是BRDF的三个函数。根据公式$(8)$,法线分布函数如下所示:
1 2 3 4 5 6 7 8 9 10 11 float NormalDistributionGGX (vec3 N, vec3 H, float roughness) float a = roughness * roughness; float aSquared = a * a; float NdotH = max(dot(N, H), 0.0f ); float NdotHSquared = NdotH * NdotH; float nom = aSquared; float denom = (NdotHSquared * (aSquared - 1.0f ) + 1.0f ); denom = PI * denom * denom; return nom / denom; }
根据公式$(9)$,菲涅尔方程的计算代码:
1 2 3 4 vec3 fresnelSchlick (float cosTheta, vec3 F0) return F0 + (1.0f - F0) * pow (1.0 - cosTheta, 5.0f ); }
根据公式$(10)$、$(11)$、$(12)$,几何函数的计算代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 float GeometrySchlickGGX (float NdotV, float roughness) float r = (roughness + 1.0f ); float k = (r * r) / 8.0f ; float nom = NdotV; float denom = NdotV * (1.0f - k) + k; return nom / denom; } float GeometrySmith (vec3 N, vec3 V, vec3 L, float roughness) float NdotV = max(dot(N, V), 0.0f ); float NdotL = max(dot(N, L), 0.0f ); float ggx2 = GeometrySchlickGGX(NdotV, roughness); float ggx1 = GeometrySchlickGGX(NdotL, roughness); return ggx2 * ggx1; }
然后就是光照部分,我实现的渲染器支持一个平行光、多个点光源。首先来看平行光部分,平行光部分因为不用考虑衰减,因而更为简单:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 struct DirLight { vec3 direction; vec3 radiance; }; uniform DirLight dirLight; void main () vec3 FragPos = texture(dposition, Texcoord).rgb; vec3 albedo = texture(dalbedo, Texcoord).rgb; vec3 normal = texture(dnormal, Texcoord).rgb; float roughness = texture(droughness, Texcoord).r; float metallic = texture(droughness, Texcoord).g; float depth = texture(droughness, Texcoord).b; float ao = texture(ddepth, Texcoord).r; if (normal.x == 0.0f && normal.y == 0.0f && normal.z == 0.0f ) { fragColor.rgb = albedo; float brightness = dot(fragColor.rgb, vec3(0.2126 , 0.7152 , 0.0722 )); brightColor = vec4(fragColor.rgb, 1.0f ); gl_FragDepth = depth; return ; } vec3 viewDir = normalize(cameraPos - FragPos); vec3 F0 = vec3(0.04 ); F0 = mix(F0, albedo, metallic); vec3 lightDir = dirLight.direction; vec3 halfwayDir = normalize(lightDir + viewDir); vec3 fresnel = fresnelSchlick(max(dot(halfwayDir, viewDir), 0.0f ), F0); float distribution = NormalDistributionGGX(normal, halfwayDir, roughness); float geometryFactor = GeometrySmith(normal, viewDir, lightDir, roughness); vec3 brdf = distribution * fresnel * geometryFactor / (4.0f * max(dot(viewDir, normal), 0.0f ) * max(dot(lightDir, normal), 0.0f ) + 0.0001f ); vec3 kSpecular = fresnel; vec3 kDiffuse = vec3(1.0f ) - kSpecular; kDiffuse *= (1.0f - metallic); fragColor.rgb = (kDiffuse * albedo / PI + brdf) * dirLight.radiance * max(dot(normal, lightDir), 0.0f ); .... }
需要特别说明的就是基础反射率部分,在上面的代码第41、42行,对于电介质我们令其基础反射率为0.04,然后根据材质的金属度在0.04和反照率直接做一个混合。然后就是点光源部分,点光源通常要有一个衰减的过程,这里我采用的衰减因子计算公式如下:
即点光的光照强度以距离的平方的倒数衰减,其中$c$是衰减系数,可由用户根据想要的效果指定。确定了衰减方程之后,我们还需要计算点光源的光体积,这是因为当光源与当前点的距离超过一定的值时,计算得到的光照值将小到可以忽略不计。因此,我们可以做这样的一个优化,当距离超过一定值时直接不计算光照,这对于拥有大量光源的场景来说是非常有意义的,它能够减少大量的计算。
那么如何知道这个距离的阈值呢?这个距离的阈值必须要刚刚好,太小则会产生明显的光照硬边,太大则优化又没有那么明显。事实上,这个距离阈值与上面的衰减因子计算(即公式$(17)$)息息相关。理想情况下,当$attenuation$变为0时,光照的贡献值也变为0。但是事实上$attenuation$不能为0,只能无限地趋于0,我们可以根据一个自己设置的阈值来求解$d$,我设置的阈值为$\frac{1}{256}$,当光照贡献值小于这个值时,可以忽略不计了:
上式中的$I_{max}$是光照颜色中的最大分量,根据公式$(18)$我们就得到了点光源的光体积,这是一个以该$d$为半径的球体。当片段位置到光源位置的距离大于这个半径时,我们直接跳过该光源的光照计算。这个光体积直接在CPU上计算一次即可:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void PointLight::setAttenuationCoff(float coff){ m_atteunationCoff = coff; GLfloat lightMax = std ::fmaxf(std ::fmaxf(m_radiance.r, m_radiance.g), m_radiance.b); m_radius = sqrt (256.0f * lightMax / (1.0f * m_atteunationCoff)); } void PointLight::setLightColor(glm::vec3 radiance){ Light::setLightColor(radiance); GLfloat lightMax = std ::fmaxf(std ::fmaxf(m_radiance.r, m_radiance.g), m_radiance.b); m_radius = sqrt (256.0f * lightMax / (1.0f * m_atteunationCoff)); }
最后完整的着色器代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 #version 330 core in vec2 Texcoord; struct DirLight { vec3 direction; vec3 radiance; }; struct PointLight { float radius; vec3 position; vec3 radiance; }; uniform vec3 cameraPos; #define MAX_POINT_LIGHT 128 uniform int pointLightNum; uniform DirLight dirLight; uniform PointLight pointLight[MAX_POINT_LIGHT]; uniform float lightAttenuationCoff; uniform mat4 lightSpaceMatrix; uniform sampler2D dposition; uniform sampler2D dnormal; uniform sampler2D dalbedo; uniform sampler2D droughness; uniform sampler2D ddepth; uniform sampler2D shadowDepth; layout(location = 0 ) out vec4 fragColor; layout(location = 1 ) out vec4 brightColor; float NormalDistributionGGX (vec3 N, vec3 H, float roughness) float GeometrySchlickGGX (float NdotV, float roughness) float GeometrySmith (vec3 N, vec3 V, vec3 L, float roughness) vec3 fresnelSchlick (float cosTheta, vec3 F0) ;float shadowCalculation (vec4 fragPosLightSpace, float bias) const float PI = 3.14159265359 ;void main () vec3 FragPos = texture(dposition, Texcoord).rgb; vec3 albedo = texture(dalbedo, Texcoord).rgb; vec3 normal = texture(dnormal, Texcoord).rgb; float roughness = texture(droughness, Texcoord).r; float metallic = texture(droughness, Texcoord).g; float depth = texture(droughness, Texcoord).b; float ao = texture(ddepth, Texcoord).r; if (normal.x == 0.0f && normal.y == 0.0f && normal.z == 0.0f ) { fragColor.rgb = albedo; float brightness = dot(fragColor.rgb, vec3(0.2126 , 0.7152 , 0.0722 )); brightColor = vec4(fragColor.rgb, 1.0f ); gl_FragDepth = depth; return ; } vec3 viewDir = normalize(cameraPos - FragPos); vec3 F0 = vec3(0.04 ); F0 = mix(F0, albedo, metallic); vec3 lightDir = dirLight.direction; vec3 halfwayDir = normalize(lightDir + viewDir); vec3 fresnel = fresnelSchlick(max(dot(halfwayDir, viewDir), 0.0f ), F0); float distribution = NormalDistributionGGX(normal, halfwayDir, roughness); float geometryFactor = GeometrySmith(normal, viewDir, lightDir, roughness); vec3 brdf = distribution * fresnel * geometryFactor / (4.0f * max(dot(viewDir, normal), 0.0f ) * max(dot(lightDir, normal), 0.0f ) + 0.0001f ); vec3 kSpecular = fresnel; vec3 kDiffuse = vec3(1.0f ) - kSpecular; kDiffuse *= (1.0f - metallic); fragColor.rgb = (kDiffuse * albedo / PI + brdf) * dirLight.radiance * max(dot(normal, lightDir), 0.0f ); vec3 pointLightRadiance = vec3(0.0f ); for (int i = 0 ;i < pointLightNum;++ i) { vec3 lightDir = normalize(pointLight[i].position - FragPos); vec3 halfwayDir = normalize(viewDir + lightDir); float distance = length(pointLight[i].position - FragPos); if (distance > pointLight[i].radius) continue ; float attenuation = 1.0f / (lightAttenuationCoff * distance * distance + 0.00001 ); vec3 radiance = pointLight[i].radiance * attenuation; vec3 fresnel = fresnelSchlick(max(dot(halfwayDir, viewDir), 0.0f ), F0); float distribution = NormalDistributionGGX(normal, halfwayDir, roughness); float geometryFactor = GeometrySmith(normal, viewDir, lightDir, roughness); vec3 brdf = distribution * fresnel * geometryFactor / (4.0f * max(dot(viewDir, normal), 0.0f ) * max(dot(lightDir, normal), 0.0f ) + 0.0001f ); vec3 kSpecular = fresnel; vec3 kDiffuse = vec3(1.0f ) - kSpecular; kDiffuse *= (1.0f - metallic); pointLightRadiance += (kDiffuse * albedo / PI + brdf) * radiance * max(dot(normal, lightDir), 0.0f ); } float shadow = 1.0f ; vec4 FragPosLightSpace = lightSpaceMatrix * vec4(FragPos, 1.0f ); shadow = 1.0f - shadowCalculation(FragPosLightSpace, 0.0f ); fragColor.xyz = ao * albedo * 0.02f + fragColor.xyz * shadow + pointLightRadiance; float brightness = dot(fragColor.rgb / (fragColor.rgb + vec3(1.0f )), vec3(0.2126 , 0.7152 , 0.0722 )); if (brightness > 0.55f ) brightColor = vec4(fragColor.rgb / (fragColor.rgb + vec3(1.0f )), 1.0f ); gl_FragDepth = depth; } float NormalDistributionGGX (vec3 N, vec3 H, float roughness) float a = roughness * roughness; float aSquared = a * a; float NdotH = max(dot(N, H), 0.0f ); float NdotHSquared = NdotH * NdotH; float nom = aSquared; float denom = (NdotHSquared * (aSquared - 1.0f ) + 1.0f ); denom = PI * denom * denom; return nom / denom; } float GeometrySchlickGGX (float NdotV, float roughness) float r = (roughness + 1.0f ); float k = (r * r) / 8.0f ; float nom = NdotV; float denom = NdotV * (1.0f - k) + k; return nom / denom; } float GeometrySmith (vec3 N, vec3 V, vec3 L, float roughness) float NdotV = max(dot(N, V), 0.0f ); float NdotL = max(dot(N, L), 0.0f ); float ggx2 = GeometrySchlickGGX(NdotV, roughness); float ggx1 = GeometrySchlickGGX(NdotL, roughness); return ggx2 * ggx1; } vec3 fresnelSchlick (float cosTheta, vec3 F0) return F0 + (1.0f - F0) * pow (1.0 - cosTheta, 5.0f ); } float shadowCalculation (vec4 fragPosLightSpace, float bias) vec3 projCoords = fragPosLightSpace.xyz / fragPosLightSpace.w; projCoords = projCoords * 0.5 + 0.5 ; if (projCoords.z > 1.0 ) return 0.0f ; float shadowFactor = 0.0f ; float currentDepth = projCoords.z; vec2 texelSize = 1.0 / textureSize(shadowDepth, 0 ); for (int x = -1 ; x <= 1 ; ++x) { for (int y = -1 ; y <= 1 ; ++y) { float pcfDepth = texture(shadowDepth, projCoords.xy + vec2(x, y) * texelSize).r; shadowFactor += ((currentDepth - bias) > pcfDepth) ? 1.0 : 0.0 ; } } shadowFactor /= 9.0 ; return shadowFactor; }
四、屏幕空间环境光遮蔽 本文前面主要介绍了PBR的直接光照,这意味着在没有被光源直接照亮的区域,依然没有产生符合物理规律的光影效果,这是因为我们还没有考虑间接光照。在实时应用中,为了实现物体的相互遮蔽效果,通常采用SSAO(即Screen Space Ambient Occlusion),实际上这是一个比较tricky的做法,但是产生的效果非常不错。
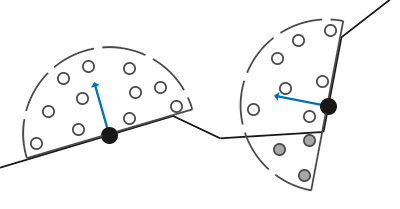
SSAO采用的原理非常简单,:对于每一个片段,我们都会根据周边深度值计算一个遮蔽因子(Occlusion Factor) 。这个遮蔽因子之后会被用来减少或者抵消片段的环境光照分量。遮蔽因子是通过采集片段周围球型核心(Kernel)的多个深度样本,并和当前片段深度值对比而得到的。高于片段深度值样本的个数就是我们想要的遮蔽因子。正如下图8所示。到这里文章篇幅有点太长了,SSAO也比较简单,因此我就不再赘述了。SSAO因子计算的核心代码:
图8 Occlusion Factor
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 #version 430 core in vec2 Texcoord; uniform vec3 samples[64 ]; uniform mat4 viewMatrix; uniform mat4 projectMatrix; uniform sampler2D dposition; uniform sampler2D dnormal; uniform sampler2D ddepth; uniform sampler2D randomNoise; uniform float farPlane; uniform float nearPlane; const float radius = 10.0f ;const int sampleNum = 64 ;void main () vec3 FragPos = texture(dposition, Texcoord).rgb; vec3 normal = texture(dnormal, Texcoord).rgb; float depth = texture(ddepth, Texcoord).r; vec2 depthTextureSize = textureSize(ddepth, 0 ); vec2 noiseTextureSize = textureSize(randomNoise, 0 ); vec2 noiseTexScale = vec2(depthTextureSize.x / noiseTextureSize.x, depthTextureSize.y / noiseTextureSize.y); vec3 randomVec = texture(randomNoise, Texcoord * noiseTexScale).rgb; vec3 tangent = normalize(randomVec - normal * dot(randomVec, normal)); vec3 bitangent = cross(normal, tangent); mat3 TBNMatrix = mat3(tangent, bitangent, normal); float occlusion = 0.0f ; for (int i = 0 ;i < sampleNum;++i) { vec3 samplePoint = TBNMatrix * samples[i]; samplePoint = FragPos + samplePoint * radius; samplePoint = vec3(viewMatrix * vec4(samplePoint, 1.0f )); vec4 tmp = vec4(samplePoint, 1.0f ); tmp = projectMatrix * tmp; tmp.xyz /= tmp.w; tmp.xyz = tmp.xyz * 0.5f + 0.5f ; float sampleDepth = texture(ddepth, tmp.xy).r; samplePoint.z /= -farPlane; float rangeCheck = smoothstep(0.0 , 1.0 , radius / (abs (depth - sampleDepth) * farPlane)); occlusion += (sampleDepth > samplePoint.z ? 0.0 : 1.0 ) * rangeCheck; } occlusion /= sampleNum; occlusion = 1.0f - occlusion; gl_FragDepth = occlusion; }
SSAO对于场景的真实感觉有着非常重要的作用,可能我们平时不会太过注意,但是却又是一个非常关键的点。下面左边就是计算得到的AO因子,最后将AO因子的乘上物体的反照率以及环境光缩放系数即可。
图9 ao因子计算结果
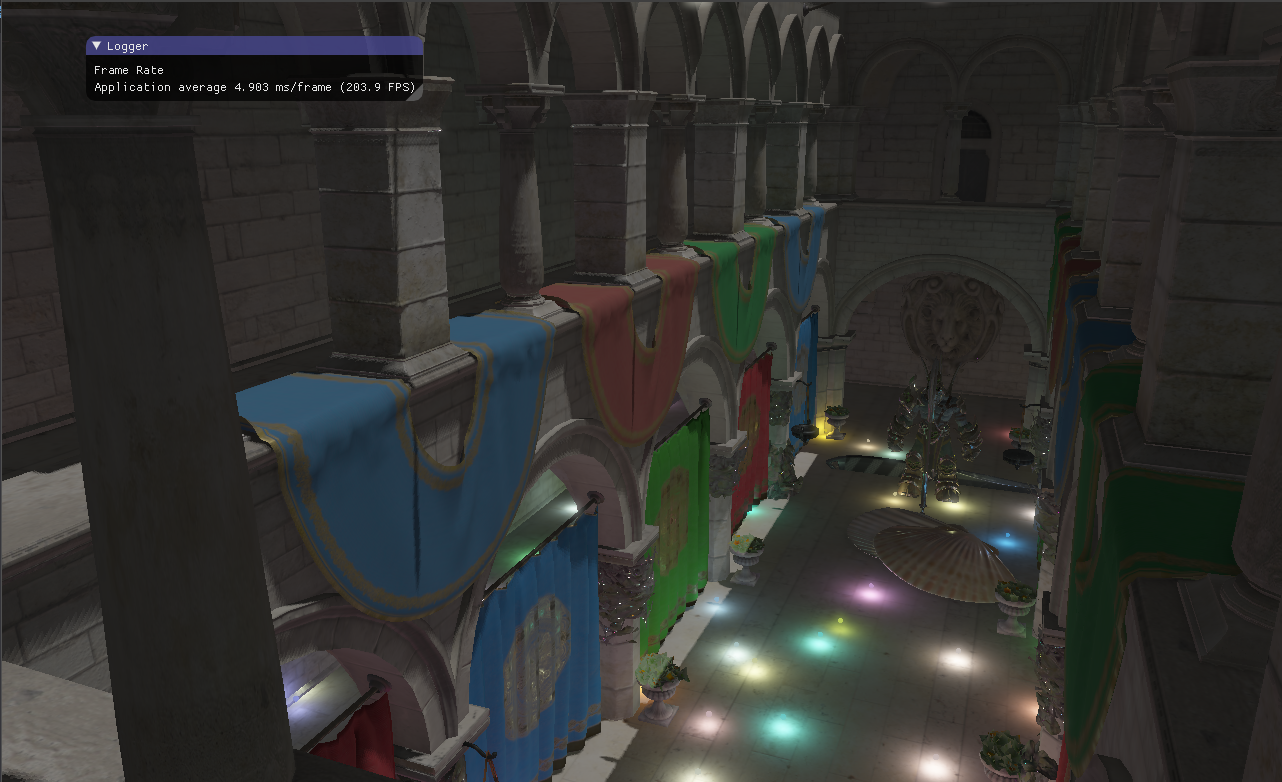
五、实现效果 除了PBR、SSAO,其他如延迟渲染、HDR、Glow Effect、因子等不再赘述。
参考资料: $[1]$ https://learnopengl.com/PBR/Theory
$[2]$ https://learnopengl.com/PBR/Lighting
$[3]$ https://learnopengl.com/Advanced-Lighting/Deferred-Shading
$[4]$ https://learnopengl.com/Advanced-Lighting/SSAO