Physically Based Rendering：采样和重建（三）

WC Yang

2020-04-11

Computer Graphics / Ray Tracer

本篇承接上一篇《采样和重建（二）》，主要包含了在对场景的辐射率采样之后的图像重建方面的内容。

以下的内容大部分整理自pbrt第三版的第七章——SAMPLING AND RECONSTRUCTION。

九、图像重建

在对场景的辐射率进行采样之后得到一系列的采样值，我们紧接着需要对这些采样值处理以显示或保存到图片中，这个就是图像的重建。根据信号处理理论，图像重建需要做以下三件事：

根据采样值重建原始的连续图像的辐射率函数$\hat L$。
对$\hat L$进行滤波，以过滤掉超出当前采样频率对应的奈奎斯特极限频率。
再对滤波之后的$\hat L$进行采样以计算每个离散像素的最终的辐射率值。

实践中我们并不需要$\hat L$的显式函数，因此前两步可以合成一步，用一个滤波函数表达。理想情况下，均匀采样的频率不低于奈奎斯特极限频率就可以完好无损地重建出原始的函数信号。但现实很残酷，完好无损的重建是不可能的。而且场景的辐射率函数通常拥有很高的频率范围，均匀的采样频率追不上，为此通常都是使用随机采样方法而非均匀采样。因为随机采样将走样现象转换成了噪声，更容易被人眼接受。

计算给定的像素$(x,y)$的最终的辐射率值$I(x,y)$，可以用如下的邻域采样值的加权平均表示：

$I(x,y)= \frac{\Sigma_i f(x-x_i,y-y_i)\omega (x_i,y_i) L(x_i,y_i)}{\Sigma_i f(x-x_i, y-y_i)}$

其中，$L(x_i,y_i)$是采样点$(x_i,y_i)$处采样得到的辐射率，$\omega(x_i,y_i)$是该采样点的贡献权重（由摄像机类返回，对于投影式摄像机，这个权重就是$1$），$f(x-x_i,y-y_i)$就是一个滤波器函数，因此这本质上就是一个滤波的过程。接下来实现各种滤波器函数。在此之前，首先创建一个Filter接口类对滤波函数$f$进行封装：

class Filter {
  public:
    // Filter Interface
    virtual ~Filter();
    Filter(const Vector2f &radius)
        : radius(radius), invRadius(Vector2f(1 / radius.x, 1 / radius.y)) {}
    virtual Float Evaluate(const Point2f &p) const = 0;

    // Filter Public Data
    const Vector2f radius, invRadius;
};

其中radius指定$x$方向$y$方向的滤波半径，Evaluate方法输入一个点p，返回这个点p出的滤波函数值f（而非滤波结果）。注意这里滤波核的中心是原点。

1、Box滤波器

图形学中最常用的滤波器就是Box滤波器，或者说均值滤波器，尽管这个滤波器的滤波效果可以说是最糟糕。Box滤波器可能会导致后走样现象的产生，因为它将高频的采样值融入到了重建值中。下图显式了一个Box滤波器，它就是一个常量函数。

Box滤波器实现起来及其简单，而且高效。对于所有在滤波核范围内的点，它都返回一个常量1.0：

class BoxFilter : public Filter {
  public:
    BoxFilter(const Vector2f &radius) : Filter(radius) {}
    Float Evaluate(const Point2f &p) const;
};

Float BoxFilter::Evaluate(const Point2f &p) const { return 1.; }

2、Triangle滤波器

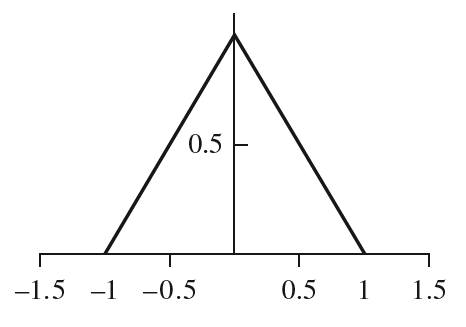
Triangle滤波器顾名思义，它的滤波函数形状就是一个三角形。如下图所示，在中心处权值为$1.0$，然后两边向外在滤波核半径内逐渐线性递减，因此Triangle滤波器本质上是实现了线性插值。

class TriangleFilter : public Filter {
  public:
    TriangleFilter(const Vector2f &radius) : Filter(radius) {}
    Float Evaluate(const Point2f &p) const;
};

实现Triangle滤波器也非常简单，以x轴为例，这里实现的是中心处函数值为radius.x，因此x方向的f=radius.x - std::abs(p.x)。y轴同理：

Float TriangleFilter::Evaluate(const Point2f &p) const {
    return std::max((Float)0, radius.x - std::abs(p.x)) *
           std::max((Float)0, radius.y - std::abs(p.y));
}

3、Gaussian滤波器

Gaussian滤波使用高斯函数（或者说正太分布函数）作为其滤波的权重函数，它的滤波效果平滑，但不可避免地带来了模糊效果。下图展示了一个一维的高斯函数，函数从中心向两边平滑递减：

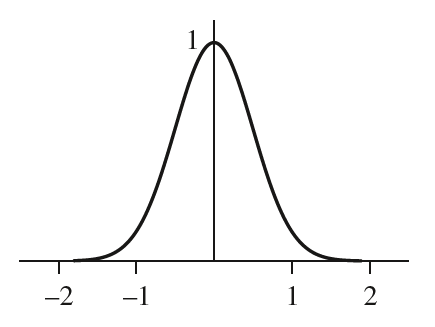
一个一维的高斯滤波函数定义如下：

$f(x)=e^{-\alpha x^2}-e^{-\alpha r^2}$

其中$\alpha$决定了高斯曲线的陡峭程度（即向两边的降低速率），$r$是滤波核半径。原本的高斯函数是$f(x)=e^{-\alpha x^2}$而非上述的公式，再减去$e^{-\alpha r^2}$是确保在滤波核的边缘上高斯函数降低至零。$e^{-\alpha r^2}$可以提前计算保存好。创建一个Gaussian滤波器类如下：

class GaussianFilter : public Filter {
  public:
    // GaussianFilter Public Methods
    GaussianFilter(const Vector2f &radius, Float alpha)
        : Filter(radius),
          alpha(alpha),
          expX(std::exp(-alpha * radius.x * radius.x)),
          expY(std::exp(-alpha * radius.y * radius.y)) {}
    Float Evaluate(const Point2f &p) const;

  private:
    // GaussianFilter Private Data
    const Float alpha;
    const Float expX, expY;

    // GaussianFilter Utility Functions
    Float Gaussian(Float d, Float expv) const {
        return std::max((Float)0, Float(std::exp(-alpha * d * d) - expv));
    }
};

二维的Gaussian滤波函数就是由两个一维的Gaussian滤波函数相乘得到（这是因为高斯函数的可分性）：

1
2
3

Float GaussianFilter::Evaluate(const Point2f &p) const {
    return Gaussian(p.x, expX) * Gaussian(p.y, expY);
}

4、Mitchell滤波器

注意到Gaussian滤波无法消除震鸣现象和模糊现象，Mitchell等人提出了一种更加优质的滤波器——Mitchell滤波器。Mitchell滤波函数如下图所示，与Gaussian函数相比，一个明显的区别就是它有两部分的函数值为负值——即负值波瓣。这负值波瓣起到了关键性的作用，它减弱了模糊现象，使得图像的高频部分变得更加锐利而不是模糊。但是负值波瓣部分不是越大越好，超过一定大小则震鸣现象将再次出现。而且因为存在负值部分，因此滤波时要注意滤波结果的值是否为负（为负值则clamp至$0$）。

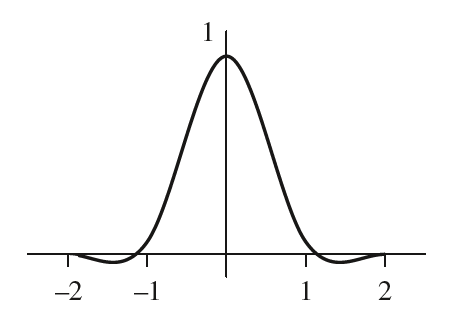
Mitchell有两个参数，分别记为$B$和$C$。Mitchell等人建议$B$和$C$的参数设置满足线性关系$B+2C=1$。一维的Mitchell滤波函数表达式如下，它的定义域范围为$[-2,2]$。因为是偶函数，我们仅讨论$[0,2]$。Mitchell滤波函数可以分成两部分，分别是$[0,1]$和$[1,2]$，这两部分分别由两个不同的三次多项式指定：

$f(x)=\frac16 \begin{cases} (12-9B-6C)|x|^3+(-18+12B+6C)|x|^2+(6-2B)& |x|<1\\ (-B-6C)|x|^3+(6B+30C)|x|^2+(-12B-48C)|x| & 1\leq |x|< 2\\ 0 & otherwise \end{cases}$

因此，可以实现Mitchell1D方法如下，这里输入的参数x默认取值为$[-1,1]$：

Float Mitchell1D(Float x) const {
    x = std::abs(2 * x);
    if (x > 1)
        return ((-B - 6 * C) * x * x * x + (6 * B + 30 * C) * x * x +
                (-12 * B - 48 * C) * x + (8 * B + 24 * C)) *
               (1.f / 6.f);
    else
        return ((12 - 9 * B - 6 * C) * x * x * x +
                (-18 + 12 * B + 6 * C) * x * x + (6 - 2 * B)) *
               (1.f / 6.f);
}

由于Mitchell滤波函数的可分性，二维的Mitchell滤波函数由两个一维的Mitchell滤波函数相乘得到：

class MitchellFilter : public Filter {
  public:
    // MitchellFilter Public Methods
    MitchellFilter(const Vector2f &radius, Float B, Float C)
        : Filter(radius), B(B), C(C) {}
    Float Evaluate(const Point2f &p) const;
    Float Mitchell1D(Float x) const;

  private:
    const Float B, C;
};

Float MitchellFilter::Evaluate(const Point2f &p) const {
    return Mitchell1D(p.x * invRadius.x) * Mitchell1D(p.y * invRadius.y);
}

4、Windowed Sinc滤波器

最后我们实现一个基于Sinc函数（译为辛格函数）的滤波器，Sinc函数定义为：

$sinc(x)=\frac{sin(\pi x)}{\pi x}$

Float Sinc(Float x) const {
    x = std::abs(x);
    if (x < 1e-5) return 1;
    return std::sin(Pi * x) / (Pi * x);
}

然后Windowed Sinc由下面两个Sinc调制而成并做截断：

$WindowedSinc(x)=Sinc(x)*Sinc(x/\tau)$

Float WindowedSinc(Float x, Float radius) const {
    x = std::abs(x);
    if (x > radius) return 0;
    Float lanczos = Sinc(x / tau);
    return Sinc(x) * lanczos;
}

可以看到多了一个控制参数$\tau$，它用于控制被截断的Sinc函数的周期数量。下图给出了一个一维的Windowed Sinc滤波函数的图像，可以看到也有负数波瓣：

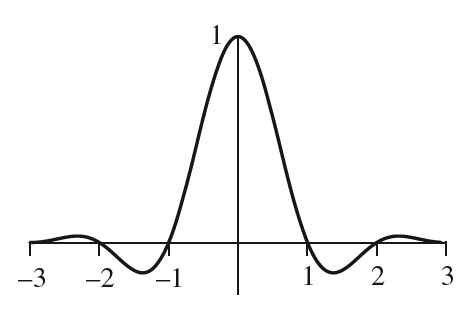
二维的滤波核函数同样由两个一维的Windowed Sinc相乘得到，见下面的Evaluate方法：

class LanczosSincFilter : public Filter {
  public:
    // LanczosSincFilter Public Methods
    LanczosSincFilter(const Vector2f &radius, Float tau)
        : Filter(radius), tau(tau) {}
    Float Evaluate(const Point2f &p) const;
    Float Sinc(Float x) const;
    Float WindowedSinc(Float x, Float radius) const;

  private:
    const Float tau;
};

Float LanczosSincFilter::Evaluate(const Point2f &p) const {
    return WindowedSinc(p.x, radius.x) * WindowedSinc(p.y, radius.y);
}

十、渲染结果比较

下面展示了使用不同采样器的渲染结果，每个像素的采样数量为$32$，从左到右、从上到下使用的采样器分别是random、stratified、halton、02sequence、maxmindist和sobol。

下面展示了使用不同滤波器的渲染重建结果，每个像素的采样数量为$64$，从左到右使用的滤波器分别是box、gaussian、mitchell、sinc和triangle。

上面的结果比较可能没那么明显，这是因为比较比较单一（仅使用了很低的采样数量，没有考虑采样器和滤波器对采样数量的收敛速度，而收敛速度又是极其重要的一个点），而且没有量化差异。

Reference

$[1]$ M, Jakob W, Humphreys G. Physically based rendering: From theory to implementation[M]. Morgan Kaufmann, 2016.